基于Seeds集和成对约束的半监督三支聚类集成
姜春茂,吴 鹏,李志聪*
(1.福建工程学院 计算机科学与数学学院,福州 350118;2.哈尔滨师范大学 计算机科学与信息工程学院,哈尔滨 150025)
0 引言
聚类分析是一种典型的无监督机器学习方法。聚类分析因为不需要给定样本的标签信息,仅通过衡量数据之间的关系就能识别数据中潜在的结构特征而受到广泛的关注。但单一的聚类算法往往采用某种理想化的数据分布假设,如K-means 算法假设样本均匀分布在球形的样本空间中,当样本分布不均匀或存在较多的噪点时,聚类效果不佳。不同的聚类算法往往存在较大的差异性,即使相同的聚类算法在参数不同时,聚类结果也往往存在差异。这限制了聚类分析的适用性。
聚类集成旨在融合多个不同的基聚类成员,从而获得一个统一的数据划分。研究表明,相较于单一的聚类算法,聚类集成能够有效提高聚类结果的稳定性、鲁棒性和准确率。Strehl 等[1]将集成学习引入聚类分析中,提出了聚类集成的概念。由于缺乏先验的标签信息,聚类集成的研究要比分类集成更加困难,其中的关键问题是如何生成多个具有差异性的基聚类,以及如何对多个基聚类结果进行融合,获得更好的聚类集成结果。Strehl 等将超图划分引入聚类集成,提出了三种基于超图划分的聚类集成算法,分别是基于类簇的相似分区算法(Cluster-based Similarity Partitioning Algorithm,CSPA)、元类簇算法(Meta-CLustering Algorithm,MCLA)和超图分区算法(HyperGraph Partitioning Algorithm,HGPA)。Zhou 等[2]提出了基于投票的聚类集成方法。Fred 等[3]提出了证据积累的概念,通过在基聚类结果中构建共协关系矩阵,分析对象间的相似性,并利用层次聚类得到了聚类结果。Wang 等[4]将传统的成对约束(即必须链接或不能链接)扩展为模糊成对约束,进而提出了一种带有模糊配对约束的半监督模糊聚类(Semi-Supervised Fuzzy clustering with Pairwise Constraints,SSFPC)。
当前聚类集成的研究以非监督聚类集成为主,未能充分利用已知的先验信息,导致难以得到更加优质的聚类集成结果。半监督聚类集成利用少量已知的先验信息,如少量标签信息或成对约束信息等提高聚类集成的质量。Ma 等[5]利用共识函数中的约束信息,提出了基于Chameleon 的半监督选择性聚类集成(Semi-supervised Selective Clustering Ensemble based on Chameleon,SSCEC)和基于Ncut 的半监督选择性聚类合集(Semi-supervised Selective Clustering Ensemble based on Ncut,SSCEN)方法。SSCEC 使用Chameleon 算法作为共识函数,并在子图分割和子图组合中处理约束信息;SSCEN使用归一化切割算法作为共识函数,并在图的二分法过程中处理约束信息。实验结果表明,这两种半监督成员选择聚类组合算法优于其他半监督算法。Xiao 等[6]设计了一种基于贝叶斯网络的半监督聚类集成模型,并通过变分法对模型进行了推理和求解。这些研究推动了半监督聚类集成的发展,但有一个值得注意的问题是:当前关于半监督聚类集成的研究依然以硬聚类为主。在硬聚类的结果中,对象与类簇之间存在明确的归属关系,即对象确定属于该类簇或对象确定不属于该类簇。在现实的复杂数据中,对象与类簇之间的关系通常是模糊和不确定性的,对象与类簇之间缺乏明确的归属关系。当可用信息不足时,强制将对象划分到某一类簇容易引起较高的误分类代价。因此现有的聚类集成算法难以精确地刻画类簇的结构特征。
Yu 等[7]将三支决策的思想引入聚类分析,并提出了三支聚类算法。不同于传统的硬聚类结果,三支聚类通过一对集合呈现一个类簇,即核心域和边界域。核心域中的数据表示确定属于该类簇,边界域中的数据表示可能属于该类簇。琐碎域表示核心域和边界域并集的补集,用来描述确定不属于该类簇的对象。三支聚类能够更加精确地刻画类簇边界模糊的现象,能够有效描述对象与类簇之间的不确定性关系。自三支聚类提出以来,多种研究成果已经涌现。如Wang等[8]借鉴数学形态学中的收缩和扩张思想,提出了一种基于数学形态学的三支聚类算法;Yu 等[9]将证据理论引入聚类分析中,提出了一种基于证据理论的密度峰值三支聚类算法;Afridi 等[10]针对含有缺失值的数据,提出了一种基于博弈粗糙集的三支聚类算法;Yu 等[11]将低秩矩阵和主动学习引入多视图聚类中,提出了一种基于低秩表示的多视图主动三支聚类算法;Jiang 等[12]利用阴影集和多粒度粗糙集的思想提出了一种三支聚类集成方法,在众多UCI(University of California,Irvine)数据集上的实验效果良好。
在聚类集成中,标签信息和成对约束信息有助于改善集成效果,然而,很少有人考虑或同时考虑这两种类型的先验知识。此外,传统的基聚类结果是二支聚类,难以精确地刻画类簇的结构特征,使得在集成阶段可能丢失一些重要信息。为了解决上述问题,本文提出了一种基于Seeds 集和成对约束的半监督三支聚类集成(Seeds-set based Three-Way Clustering Ensemble,STWCE)方法。首先,基于标签传播算法(Label Propagation Algorithm,LPA),STWCE 方法利用标签信息构建具有差异性的基聚类成员集合;然后提出一种新的方法来构建一致性相似矩阵,并利用成对约束信息对相似矩阵进行调整;最后,使用三支谱聚类对相似矩阵聚类,得到最终集成后的聚类结果。本文主要工作总结如下:
1)将三支决策理论引入半监督聚类集成,利用不同类型的先验信息设计了一种三支标签传播算法来生成基聚类成员。
2)通过在均匀的成对空间中比较不同区域的对象来区别基聚类成员所做出的贡献,即采用一种新的规则对基聚类成员进行不同的权重表示;并通过将不同基聚类成员结果进行统一表示,有效解决了未对齐的问题。
3)使用基于三支决策思想的谱聚类方法对一致性相似矩阵进行聚类,使集成结果收敛于全局最优解。每个类簇由一对集合进行表示,更好地表现出对象与类簇之间的归属关系。
1 相关工作
1.1 聚类集成
给定一组数据U={x1,x2,…,xn},n表示数据样本的个数。聚类集成通过在数据U上重复执行m次聚类得到一组基聚类结果Π={π1,π2,…,πm},式中πi=是第i次基聚类的结果表示第i次基聚类的第j个类簇。聚类集成主要包括两个步骤:基聚类Π的生成和一致性函数Γ的设计。在第一步中,主要工作是使用不同的生成机制生成一组不同的聚类结果,例如不同参数下的同一算法[12]、选择不同算法[13]和选择不同的对象子集[14-15]等;第二步是聚类集成的关键步骤,对得到的基聚类成员进行集成来得到最终的聚类结果。现有的聚类集成方法主要分为三类:基于图的方法[16]、基于数据点间相似度的方法[17]和基于特征的方法[18]。基于图的方法将聚类集成问题表示成超图的形式,并调用图划分算法求解;基于数据点间相似度的方法通过建立样本间的相似矩阵,再基于相似度聚类的方法来得到聚类结果;基于特征的方法则使用每个基聚类成员内各样本的聚类标签作为新的特征来得到最后的聚类结果。
1.2 三支聚类的基本形式
传统的聚类算法是一种硬聚类或者说二支聚类的结果,即对象和类簇之间的关系是明确的,对象确定属于该类簇或对象确定不属于该类簇。给定一组数据U={x1,x2,…,xn},二支聚类通过单个集合Ci表示一个类簇。所划分的类簇内具有较高的相似性,而类簇间具有较高的相异性。给定一组类簇集合C={C1,C2,…,Ck},将U中所有的对象划分到k个类簇中,并且k个类簇满足如下条件:
1)类簇不能为空,即每个类簇至少包含一个对象:Ci≠∅(i=1,2,…,k);
3)每一个对象只能属于一个类簇,即类簇之间的交集为空:Ci∩Cj=∅(i≠j)。
不同于二支聚类,三支聚类将每个类簇用一对集合进行表示:Ci={Co(Ci),Fr(Ci)},即类簇Ci由核心域Co(Ci)和边界域Fr(Ci)两个子集组成。类簇Ci的琐碎域表示为Tr(Ci)=U-Co(Ci) -Fr(Ci),表示由确定不属于类簇Ci的对象组成的集合。类簇Ci的三个域满足如下条件:
上述4 个条件说明任何一个类簇的核心域、边界域和琐碎域之间的并集为论域OB,且核心域、边界域和琐碎域两两互不相交。三支聚类的k个类簇满足如下条件:
上述三个条件说明任意一个类簇的核心域不为空,所有类簇的核心域和边界域的并集为论域OB,任意两个类簇的核心域的交集为空。
1.3 半监督聚类
按照不同的监督信息,半监督聚类可分为基于成对约束信息的半监督聚类和基于标签信息的半监督聚类。
成对约束信息有must-link 和cannot-link:must-link 指两个对象属于同一个类别;cannot-link 指两个对象不属于同一个类别。Wagstaff 等[19]将成对约束的思想运用到传统K-means 算法中,提出了Cop-Kmeans 算法;Zheng 等[20]将成对约束思想引入层次聚类算法,在层次聚类中也可以使用成对约束;Yang 等[21]通过对cannot-link 进行广度搜索来解决Cop-Kmeans 中的约束冲突问题,并通过MapReduce 降低计算复杂度。
相较于成对约束信息,标签信息可以直接判断数据点的类别。Qin 等[22]系统性回顾了半监督聚类,尤其是对基于约束信息的半监督聚类方法;Zhou 等[23]提出了标签传播算法,该算法是基于图的半监督聚类的代表性算法;Yu 等[24]同时考虑特征空间和样本空间的渐进式子空间的方法以获得更准确的半监督聚类结果;Fang 等[25]提出了一种基于低秩表示的半监督子空间聚类方法,将低秩表示框架与高斯场和谐函数结合,通过融合标签信息完成相似矩阵的构造和子空间聚类。
半监督聚类算法在很多领域等都有着广泛的应用。在以上研究中,只使用了单一的监督信息来辅助聚类。然而,先验信息不仅有成对约束,还存在标签信息,不同类型的先验信息具有不同的意义,因此,如何融合不同类型的先验信息达到聚类结果的目的有着重要的研究意义。
2 基于Seeds 集和成对约束的半监督三支聚类集成方法
本章首先阐述了基于Seeds 集和成对约束的半监督三支聚类集成(STWCE)方法的基本思想,然后详细介绍了该方法的关键步骤。
2.1 STWCE的基本思想
图1 给出了STWCE 方法的基本框架,其中:p为打标问询次数,P为最大问询次数。由图1 可知,该方法首先采用LPA 生成多个具有差异性的基聚类集合,即Π={π1,π2,…,πm}。每个节点的标签更新取决于其邻居节点,更新效果受节点初始输入和标签更新顺序的影响,因此每次结果存在不确定性,强制将不确定的对象分配到某一类可能会降低聚类的结果,而三支决策思想正是解决聚类算法结果不稳定和不精确问题的重要方法之一。通过将每个类由两个集合进行表示,减少由于强制分类而带来的聚类效果的降低,更好地呈现出对象与类簇之间的关系。
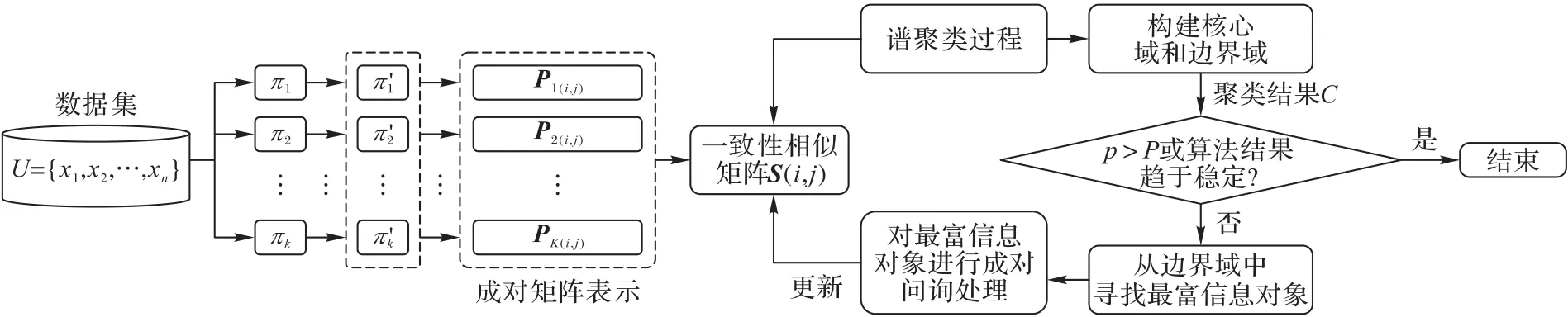
图1 STWCE方法的框架Fig.1 Framework of STWCE method
在得到基聚类集合后,共协关系矩阵可能只得到了部分点的相似关系,例如,对象x在不同基聚类结果中可能有不同的归属关系。另外,不同的基聚类成员聚类后的标签可能并不对应,因此,定义一组规则来统一表示不同基聚类成员的结果,并针对不同区域的对象采用不同的策略进行集成,以更好地描述对象间的相似关系,并利用成对约束信息优化调整一致性相似矩阵。最后通过三支谱聚类方法对一致性相似矩阵聚类,得到最终的集成结果。
2.2 基聚类成员生成
基聚类成员的产生方法多种多样,如采用不同的聚类算法、采用不同参数下同一聚类算法、在特征子空间进行聚类和在数据子空间进行聚类等。然而,这些成员生成方法未考虑到数据集中已有的标签信息,本文设计了一种三支标签传播算法(TW-LPA),利用已有标签信息构成的Seeds 集对原始数据集进行聚类。
LPA 只需利用少量的标签信息指导就可以发现未标记数据的内在特性、分布规律,进而预测和传播未标记数据的标签,合并到标记的数据集中。LPA 通过相似节点之间的标签的传递来学习如何进行聚类,所以它不受数据分布的限制。算法具有线性时间复杂度,广泛应用于大规模数据处理和挖掘。然而,该算法每个节点的标签更新取决于其邻居节点,更新效果受节点初始输入和标签更新顺序的影响。因此,LPA 的每次结果存在不确定性,而三支决策思想正是解决聚类算法结果不稳定和不精确的重要方法之一。为此,将多次运行的LPA 的结果作为基聚类的结果。
给定原始数据集U={x1,x2,…,xn},用Π={π1,π2,…,πK}表示基聚类成员集合,πi表示第i个基聚类的结果。数据集中前l个对象带有数据类标签,后n-l个对象不带数据类标签。给定已知对象的标签集合Y={y1,y2,…,yl},集合U的前l个对象在Y中一一对应。给定图结构G=(U,W),其中:U为数据集合在图G中的节点;W代表节点之间的相似性关系,即节点间的权重。计算节点间权重Wij:
定义一个n×n的概率传播矩阵P,节点i的标签传递给节点j的概率Pij为:
其中:Pij表示节点i的标签传递给节点j的概率。
通过概率传递,使概率分布集中于给定类别,然后通过边的权重值来传递节点标签。在通过LPA 得到C={C1,C2,…,Ck}时,可能会得到如图2 的结果:将每个类簇用一个集合进行表示,x1与x2分别被聚类到C1和C2中,但从图2 中可以看到强制性划分到一个类中可能是错误的。因此,引入三支聚类,并借鉴k近邻的思想,设计一种三支标签传播算法(TW-LPA),将LPA 的结果进行再次划分,采用Dist(x)(距离该点最近的t个点组成的集合)对每个类别的对象进行划分,将每个类簇进一步划分为核心域Co(Ci)和边界域Fr(Ci)两个子集,更好地展现对象与类簇的归属关系,从而减少在基聚类阶段由于强制划分某些对象带来的信息丢失导致聚类效果的降低。
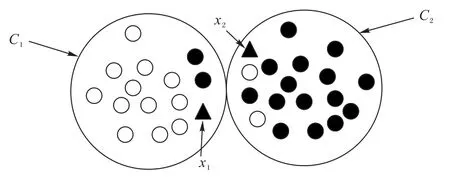
图2 对象与类簇的归属关系Fig.2 Belonging relationships between objects and class clusters
首先,考虑对象xi的Dist(xi),xi∈Ci,设arg maxDist(xi)代表距离该点最近的t个对象中数量最多的集合,若arg maxDist(xi) ∩Ci≥t,将xi分配到 该类的 核心域,即xi∈Co(Ci),否则,xi∈Fr(Ci)。此外,对于对象xj∉Ci,如果arg maxDist(xj) ∩Ci=∅,将xi分配到边界域,即xj∈Fr(Ci)。在进行n次之后,得到了新的标签传播结果。运行TW-LPA获得集合Π={π1,π2,…,πK}。具体流程见算法1。
算法1 基于TW-LPA 的基聚类成员生成。
2.3 半监督三支聚类集成
在得到由TW-LPA 产生的具有不同差异的基聚类成员集合Π={π1,π2,…,πK}后,将构建一致性相似矩阵,并利用成对约束信息对一致性相似矩阵进行优化调整。最后利用三支谱聚类对调整后的相似矩阵聚类,得到最终的集成结果。
2.3.1 半监督三支聚类集成
利用无类属数据内部存在的结构先验信息,同时结合成对约束信息汇总来自基聚类成员集合Π的信息构造相似矩阵。
对于每个基聚类成员πd(1 ≤d≤K)的结果,将它的每个类利用核心域Co(Ci)和边界域Fr(Ci)两个集合进行表示。相较于传统的硬聚类和软聚类表示方法,三支聚类的表示更加直观地展示了对象与类簇之间的归属关系,位于核心域中的对象比边界域的对象更具有可信度。此外,不同基聚类通过聚类得到的结果可能是不对齐的,与监督学习不同,聚类后的结果仅表示数据的聚类特征,将不同的聚类结果直接进行比较并不可行。例如,如图3 所示,对象x在不同的基聚类成员中可能有不同的归属关系。
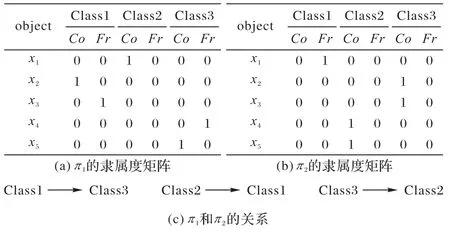
图3 对象x在不同的基聚类成员中的归属关系Fig.3 Belonging relationships of object x in different base cluster members
定义以下规则用来统一表示不同基聚类成员的结果。设P=[P(i,j)]是一个n×n的矩阵,其中,P(i,j)是xi和xj之间的相似度。
1)如果对象xi和对象xj属于同一个类Ci,同时有xi∈Co(Ci)和xj∈Co(Ci),则P(i,j)=λ+;
2)如果对象xi和对象xj属于同一个类Ci,同时有xi∈Co(Ci)和xj∈Fr(Ci),则P(i,j)=λ;
3)如果对象xi和对象xj属于同一个类Ci,同时有xi∈Fr(Ci)和xj∈Fr(Ci),则P(i,j)=λ-。
其中,0 <λ-<λ<λ+<1。
根据式(3),将不同的基聚类成员结果进行统一表示。
根据所提出的表示方法,当有K个基聚类成员进行集成时,可以将每个基聚类成员的结果保存到一个n×n的成对矩阵中。设P=是来自K个基聚类成员的一组成对矩阵,其中,Pt=[Pt(i,j)]是用来保存来自第t个基聚类成员的n×n的成对矩阵。在给定基聚类成员集合Π={π1,π2,…,πK}的情况下,可以找到所有基聚类成员间的一致性相似矩阵S的元素S(i,j)如下:
得到相似矩阵S后,利用成对约束信息优化调整相似矩阵S,使对象xi和xj在一个类簇中更紧凑,在不同类簇中更离散。对象xi和xj的相似性由Sij和Sji表示,Sij和Sji是相似矩阵S中的元素。如果对象xi和xj标记在同一个类簇中,满足must-link 关系,即(xi,xj) ∈ML,相似矩阵S中相应的元素更新为1;相反,如果xi和xj不属于同一个类簇,满足cannot-link关系,即(xi,xj) ∈CL,相似矩阵S中相应的元素更新为0。
采用以下的策略进行对S(i,j)进行调整:
算法2 相似矩阵构造算法。
根据式(3)计算Pt(i,j)
2.3.2 三支谱聚类
在上一步处理中得到了一致性相似矩阵,现在将定义一个划分准则,目的是使同一类簇的对象更紧凑,不同类簇的对象更分散。由于求图划分的最优解是一个NP 难的问题,一个很好的解决方法是考虑问题的连续放松形式,将原问题转换为求图的Laplacian 矩阵的谱分解。
谱聚类是一种基于图划分理论的方法,能对任意形状的数据进行划分且收敛于全局最优解。三支谱聚类是将三支决策思想和谱聚类方法相结合,将每个类簇由一对集合进行表示Ci={Co(Ci),Fr(Ci)},核心域Co(Ci)和边界域Fr(Ci)两个子集构成该类簇的上界。
三支谱聚类算法主要过程分为两步:1)对一致性相似度矩阵通过谱聚类方法获得每个类簇的上界;2)借助于三支决策思想,基于q邻域将每个类簇的上界进一步划分为核心域Co(Ci)和边界域Fr(Ci)两个子集。基本流程如算法3 所示。
算法3 三支谱聚类。
2.4 复杂性分析
基聚类算法阶段:设基聚类算法的个数为ε(ε≥2),第i(i∈[1,ε])个基聚类算法的复杂度为φi,则所有的基聚类算法的复杂度为
集成阶段:计算一个基聚类成员n×n的成对关系矩阵复杂度为O(n2),那么计算整个基聚类成员集合的复杂度是O(n2k)。构建基于成对约束信息监督矩阵对CTS(Connected-Triple-based Similarity)矩阵进行修改的复杂度为O(n2)。
谱聚类阶段:进行谱聚类的时间复杂度为O(n3),构造核心域和边界域的时间复杂度为O(n2k)。
所以,STWCE 算法的复杂度约为:
3 实验与结果分析
3.1 实验数据与评价标准
采用UCI 数据中的7 个数据集进行实验。其中3 个是二类的,4 个是多类的,维度分布有高有低。表1 给出了这些数据集的相关信息描述。
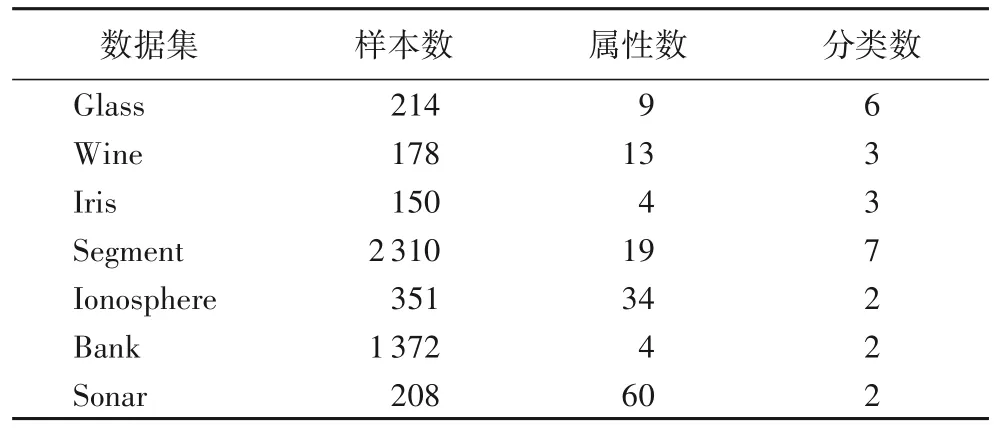
表1 实验数据集相关信息描述Tab.1 Information description of experimental datasets
实验采用目前三种广泛使用的聚类性能评价指标:
1)归一化互信息(Normalized Mutual Information,NMI)。NMI 用于评价对数据集聚类后的结果与数据集的真实结果之间的相似程度。设C为对数据集聚类后的结果,Y为数据集的真实结果,NMI 计算公式如下:
式中:I(X;Y)=H(X) -H(X|Y),反映了两个变量X和Y之间的互信息;H(X)表示变量X的香农熵;H(X|Y)表示基于给定Y的情况下X的条件熵。RNMI∈[0,1],值越大代表聚类效果越好。
2)调整兰德系数(Adjusted Rand Index,ARI)。ARI 衡量的是两个数据分布的相似性。ARI 计算公式如下:
其中:a表示在C与Y中都是同类别的元素对数,b表示在C与Y中都是不同类别的元素对数表示数据集中可以组成的对数。RARI∈[ -1,1],值越大意味着聚类结果与真实情况越吻合。
3)F 测度(F-Measure)。该指标综合了精确率和召回率评估标准,反映了任意一对样本的正确归类的准确性。F-Measure 的值越高越好,它的计算公式如下:
其中:P表示精确率,R表示召回率。
3.2 实验结果与分析
3.2.1 算法性能比较
实验首先选取LPA 作为基聚类器,运行20 次。由于LPA 的不稳定性,将会得到20 个有差异性的基聚类结果;然后通过本文方法构造一致性相似矩阵,利用成对约束信息对一致性相似矩阵进行调整,再经过三支谱聚类得到集成后的结果C。
实验中采取的对比算法有CSPA[1]、HGPA[1]、MCLA[1]、LPA[23]、Cop-Kmeans 算法[19]、限制性投射半监督的谱聚类集成(Constraint Projections for Semi-Supervised Spectral Clustering Ensemble,CPSSSCE)算法[25]。为了公平对比,从每一类数据集中抽取5%的标签样本,标签样本作为基聚类算法的Seeds 集;同时从每一类Ground-Truth 的成对约束信息中选出20%的必连信息和20%的不连信息,作为成对约束的先验知识。本文中的λ-、λ和λ+分别设置为0.3、0.5和0.7。
表2~4 分别概括了7 个数据集上给予不同类别相同比例的监督信息下,本文方法STWCE 以及对比的6 种方法的ARI值、NMI 值和F-Measure 值,加粗表示最优值。从实验结果可以看出,这7 种方法在不同的数据集上都获得了不同程度的聚类效果,而STWCE 的三个评价指标在绝大多数据集上都获得了相对较好的聚类集成效果,说明综合考虑标签信息和成对约束信息的融合以及本文所提出的集成策略能够改善聚类效果。
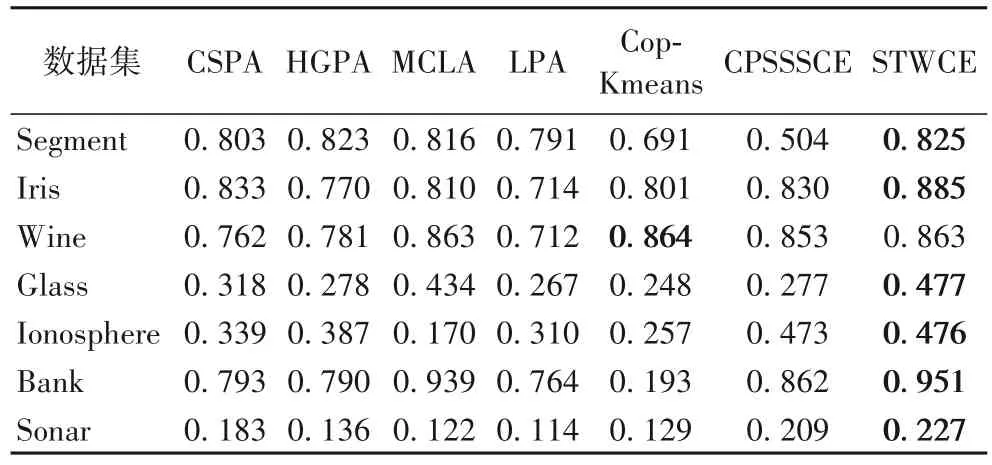
表2 不同算法的ARI值Tab.2 ARI values of different algorithms
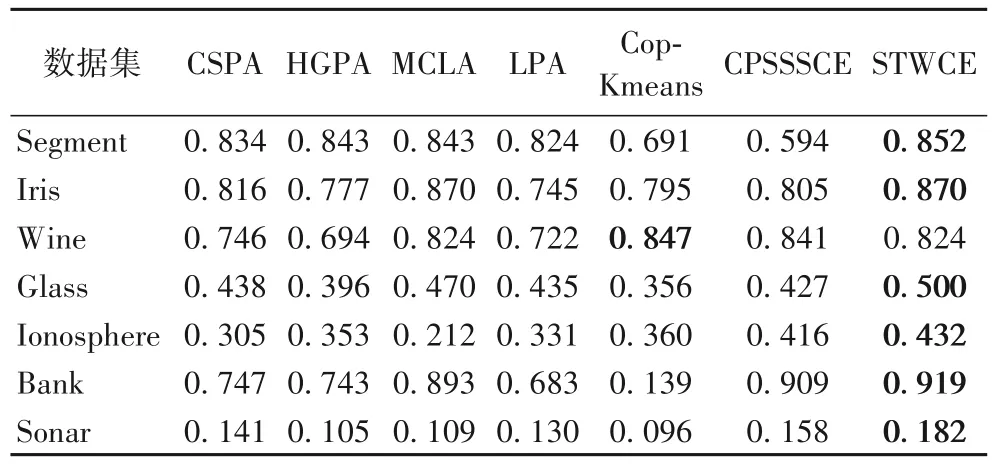
表3 不同算法的NMI值Tab.3 NMI values of different algorithms

表4 不同算法的F-Measure值Tab.4 F-measure values of different algorithms
3.2.2 一致性相似矩阵分析
为了更好地说明本文提出的半监督三支聚类集成方法构成一致性相似矩阵的效果,在不同的数据集上使用不同比例的先验信息,采用三种指标与传统的CO-association(CO)矩阵和CTS 矩阵算法进行对比。不同算法采用相同的基聚类算法并在给予相同比例的先验信息下进行实验,部分结果如图4 所示。从图4 可以看出:随着给予的先验信息的比例增大,三种评价指标都有逐渐增加的趋势;但是当提供的先验信息达到一定值之后,这些指标的增长趋势都略显减缓。

图4 不同先验信息下数据集Segment的ARI、NMI和F-Measure对比Fig.4 Comparison of ARI,NMI and F-Measure of dataset Segment under different priori information
此外,在大部分的数据集上,在先验信息不足的情况下,可以看出本文方法相较于另外两个算法有更好的集成效果。这说明相对于传统方法,三支聚类更加直观地展示了对象与类簇之间的归属关系,经过不同的规则处理后的基聚类集合采用不同的规则进行集成,充分考虑了不同成员的不同贡献,在大部分数据集上相对于传统的CO 矩阵算法和CTS 矩阵方法拥有更优的聚类性能。
4 结语
本文提出了半监督的三支聚类集成方法,它能有效利用有限的先验知识,同时融合标签信息和成对约束信息。使用连接三元组构造相似矩阵,并利用成对约束信息对相似矩阵进行调整,通过三支谱聚类进行聚类,最后得到聚类集成结果。
在多个数据集上评估了该方法,得出以下结论:1)使用标签传播算法作为基聚类算法,不仅可以利用标签传播算法的优势,同时又能避免标签传播算法不稳定的问题;2)使用基于三支聚类的方法来集成基聚类成员构建相似矩阵,并使用成对约束信息进行修改,在获得了优质的相似矩阵的同时避免了基聚类成员非对齐的问题,同时考虑了不同基聚类成员之间的贡献不同的问题;3)通过结合不同类型先验信息,可以有效提高聚类集成的性能;4)使用三支谱聚类对相似矩阵进行聚类得到集成后的结果,不仅能对任意形状的数据进行划分,且收敛于全局最优解,同时将每个类簇用核心域和边界域进行表示,更加直观地展示了数据对象确定属于或可能属于某个类簇。
在未来的工作将从两个方面进行考虑:一是考虑基聚类的质量,去除一些低质量的基聚类;二是引入主动学习,进一步提高成对约束的质量。

