混合禁忌搜索的车间调度遗传算法研究
管 赛,熊禾根
(武汉科技大学 机械自动化学院,武汉 430081)
0 引言
作业车间调度问题(Job Shop Scheduling Problem,JSP)是典型的NP-hard 问题,是目前研究最为广泛的一类调度问题,其存在于制造、物流、汽车等众多领域的实际生产中,故研究内容具有重要的理论意义和工程价值。
调度问题的求解方法可分为两类:精确求解方法和近似求解方法。精确求解方法包括解析法、穷举法、分支定界法等;近似求解方法包括基于规则的构造性方法、邻域搜索方法以及人工智能方法等。其中邻域搜索中的遗传算法(Genetic Algorithm,GA)结构简单、易于实现,且能获得较好的求解结果,所以被作为应用最广的智能优化算法,广泛应用于JSP 的求解之中。但标准遗传算法存在早熟收敛,解的稳定性差等缺点。对此何斌等人[1]提出一种改进遗传算法来求解作业车间调度问题,通过采取新的个体适应度计算方法,多种交叉操作随机选择,自适应交叉变异参数调整策略,来提升遗传算法的性能。张超勇等人[2]提出一种局部邻域搜索的遗传算法求解JSP。该算法采用新的POX 交叉算子,基于邻域搜索的变异算子,以及基于关键路径邻域的局部搜索,以改善解的质量。郑先鹏等人[3]提出的改进遗传算法采用精英保留策略,并结合改进自适应算子对问题进行求解,提升了求解JSP 的能力。王玉芳等人[4]提出了一种改进混合模拟退火算法,该算法采用自适应策略对概率进行动态调整,选择一种基于工序编码新的IPOX 交叉算子,同时加入有记忆功能的模拟退火算法,优化了JSP 的求解结果。禁忌搜索是一种全局寻优算法,搜索过程中能跳出局部最优解,同时具有良好的寻求优良解的能力,能有效提升算法的运算效率,实现高效搜索[5]。标准遗传算法虽然具有较强的全局搜索能力,但局部搜索能力较弱,在迭代过程中易早熟且陷入局部最优解。因此,本文提出一种混合禁忌搜索的改进遗传算法(Improved Tabu Search Genetic Algorithm,ITSGA),在原有的标准遗传算法基础上加入禁忌搜索算法,并改进算法流程,加入多种交叉方式的随机选择来提高种群的多样性以及产生优质解,同时加入局部邻域搜索对解进行微调,改善解的质量,达到寻找全局最优解的目的。
1 JSP 问题描述
JSP 可描述为:用m台机器加工n个工件,每个工件i都包含一系列工序,给定每道工序Oij的加工机器及加工时间pij。约束条件为:
(1)同一时刻一台机器只能加工一道工序;
(2)工件不能在同一台机器上多次加工;
(3)不考虑工件加工优先权且工序加工过程不能中断。
建立JSP 数学模型如下:
其中,目标函数F为最小化最大完工时间;Ci为工件i的最大完工时间;式(1)~式(3)表示工艺约束条件决定的工件上各工序先后操作顺序,以及加工各工件的机器先后顺序;Cik、pik分别为工件i在机器k上的完工时间和加工时间;M为一足够大正数;式(4)、式(5)中定义决策变量aihk和xilk,分别确定同一工件在不同机器上的加工先后顺序和同一机器上不同工序的加工先后顺序,
2 ITSGA
ITSGA 算法采用基于工序编码的编码方式来表示个体,具有在进行染色体置换操作后总能得到可行解的优点。种群初始化方式为随机生成初始种群,以最小化最大完工时间为评价指标,采用轮盘赌选择算子来进行个体选择,同时为了保留优秀个体,加快种群收敛速度,加入精英保留策略。在每次选择时,将最优基因直接复制保留下来,以便个体的优良性状能遗传到子代中。
个体适应度函数定义为
其中,MS(g)表示个体g对应的最大完工时间,MSmax为种群中的最大值。
2.1 随机选择多种交叉方式
交叉操作是遗传算法的核心操作,直接决定迭代过程中解的优劣情况和算法的全局搜索能力。本文提出迭代过程中多种交叉方式随机选择,以增加求解结果的多样性。以下列出一些在求解JSP 时用到的交叉操作,随机选择的方式为等概率随机选择。
POX 交叉[6]示意图如图1 所示,随机划分工件集{1,2,3,…,n} 为两个非空子集J1、J2;将父代P1、P2中包含J1的工件复制到子代C1、C2中,保留原位置;复制父代P1中包含J2的工件到子代C2,复制父代P2中包含J2的工件到子代C1,保留其顺序。图1说明了POX 算子交叉过程。
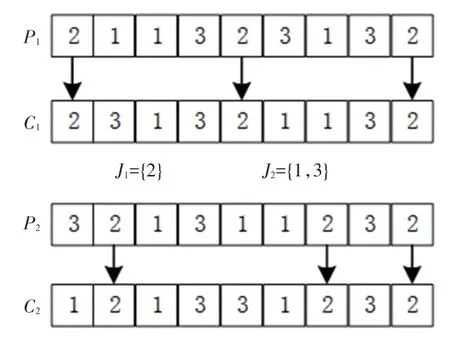
图1 POX 交叉Fig.1 POX crossover
2.1.1 OX 交叉
OX 交叉操作的示意如图2 所示。父代中随机生成两个基因座(假设4 和6),以生成子代C1为例,将父代P1基因片段323 继承给子代C1,以父代P2第7 个基因座作为第一个基因,从右往左生成临时基因编码{232321311},再根据对应位置将基因片段在临时基因编码中一一剔除{232321311} →{221311},最后再将剔除后剩余的基因片段放入子代C1中。同理,子代C2的生成过程与上述类似。
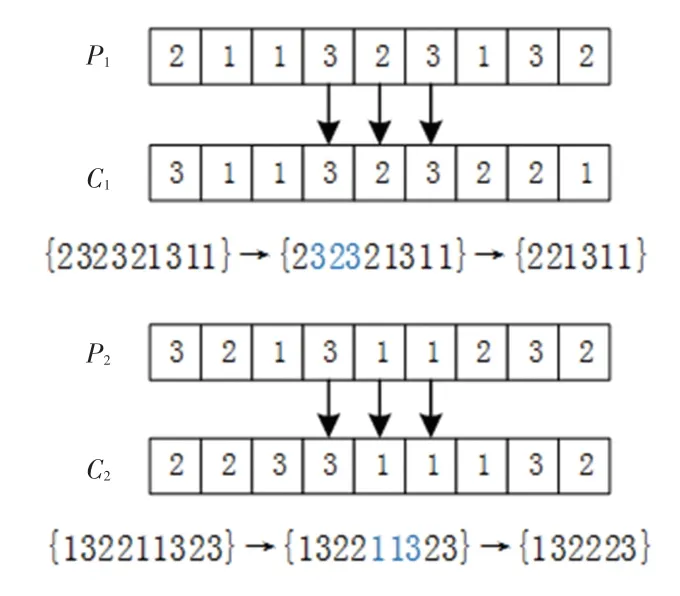
图2 OX 交叉Fig.2 OX crossover
2.1.2 PMX 交叉
PMX 交叉操作的示意如图3 所示。随机选择两个基因座(假设4 和7),得到映射关系3(工件3第一道工序)←→1(工件1 第三道工序)、1(工件1第三道工序)←→1(工件1 第二道工序),将父代P1的基因片段3231 继承给子代C1并保留原位置,再根据映射关系替换父代P2中非选中基因片段{321xxxx32}→{121xxxx32},将替换后的片段放入子代C1中,生成子代C1。同理子代C2的生成过程与上述类似。

图3 PMX 交叉Fig.3 PMX crossover
2.2 局部邻域搜索
关键路径的变化是改变最大完工时间的关键,本文采取基于关键块的快速邻域搜索方式[7-9],其流程如下:
步骤1确定当前解的关键路径和全部关键块。
步骤2设计邻域构造为交换关键块中的两个工序。3 种交换方式为:
(1)选择关键块中的首工序与块中任一工序进行交换;
(2)选择关键块中任意两个内部工序进行交换;
(3)选择关键块中的尾工序与块中任一工序进行交换。
步骤3通过随机选择来确定关键块中工序的交换方式。
步骤4将经过局部邻域搜索操作后的解添加到种群中。
3 算法验证
为了验证ITSGA 算法在求解作业车间调度问题的有效性,将本文算法与改进粒子群(Improved Particle Swarm Optimization,IPSO)算法[10]、量子鲸鱼优化(Quantum Whale Optimization Algorithm,QWOA)算法[11]、改进混合遗传模拟退火(Improved Genetic Simulated Annealing Algorithm,IGSAA)算法[4]进行对比。算法采用python 编程,在2.40 GHz处理器的Windows10 系统下运行。参数设置如下:
种群规模P =100,最大迭代次数200,交叉概率pc =0.9,变异概率pm =0.1,禁忌表长度为最大迭代次数。
表1 中,C∗为已知最优解;best 为运行10 次得到的最优解;avg 为连续运行10 次得到的平均值;加粗数据表示已经达到最优解。选取benchmark 中关于JSP 的若干算例进行验证。
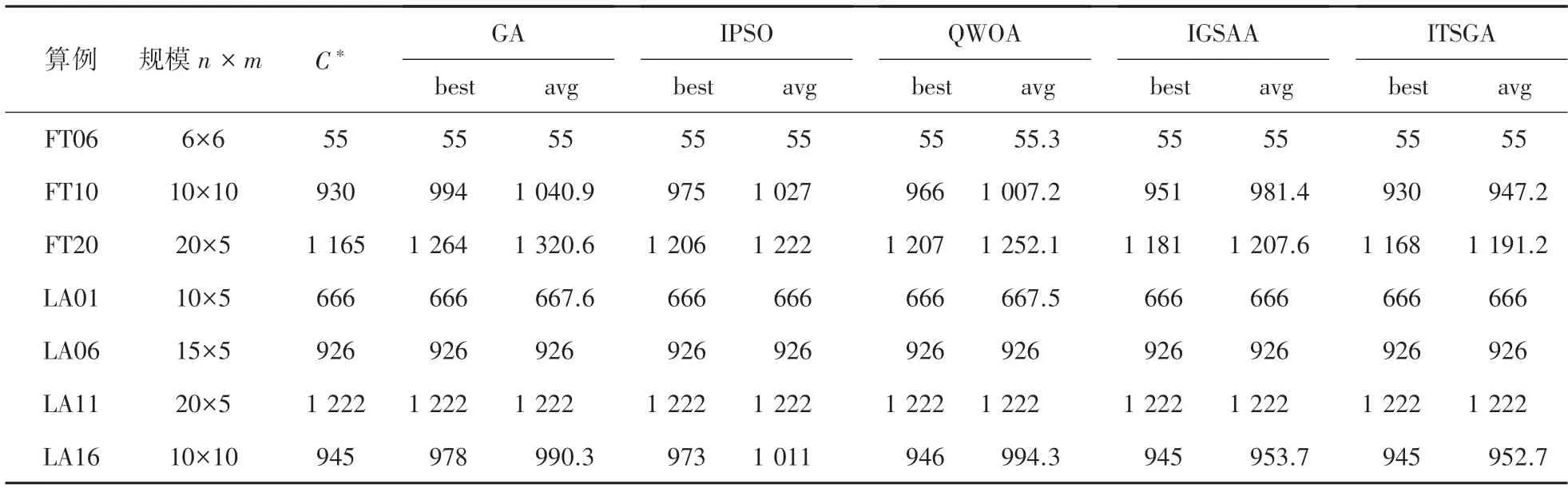
表1 各算法对benchmark 问题求解结果比较Tab.1 Comparison of the results of benchmark problem by different algorithms
从表1 中所列数据可以看出,ITSGA 算法对于表格算例中求解的最优值和平均值均优于其它算法。对于除FT20 外的其他算例均已达到最优解,这是其他算法所未能达到的,且本文算法求解FT10、FT20 得到的平均值都要明显优与其他算法。
以求解机器数量较多的FT10 为例,进一步说明ITSGA 的有效性。ITSGA 算法在求解FT10 得到的最优值和平均值都大大优于算法GA,更易跳出局部最优解,且在迭代初期就能快速收敛,说明加入的禁忌搜索算法和多种交叉方式随机选择起到了很好的作用。同时,精英保留策略也能够使子代更好地继承父代的优良性状;局部邻域搜索则提高了算法达到最优解的可能性。图4 为运用ITSGA 求解算例FT10 得到的甘特图,图中O1,2中1 表示工件号,2 表示工序号。

图4 ITSGA 求解FT10 得到的甘特图Fig.4 Gantt chart obtained by ITSGA solving benchmark FT10
4 结束语
本文提出的ITSGA 算法通过融合禁忌搜索和局部邻域搜索的改进,增强了求解JSP 的寻优能力,既有一定的全局寻优能力,能很好地避免陷入局部最优解,提高了算法的求解效率。将本文算法应用于求解若干基准问题时得到了较好结果,与传统遗传算法的求解结果相比均有较大的提升,经过与其它改进算法的比较结果,验证了ITSGA 算法的有效性。
——基于人力资本传递机制
——基于子女数量基本确定的情形

