延迟敏感约束下的多址边缘网络中资源联合分配

葛志辉,刘子萌,王 哲,李陶深

1(广西大学 计算机与电子信息学院,南宁 530004)

2(广西民族大学 人工智能学院,南宁 530005)

1 引 言

5G技术的发展与广泛部署促使移动网络在原有通信服务基础上,产生了诸多垂直型服务,如自动驾驶,虚拟/增强现实(Virtual Reality/Augment Reality,VR/AR),车联网,远程手术等.这类垂直型服务的实现历来与移动网络的计算能力和极短的时延有着十分重要的关系,然而,受限于用户设备的容量和能耗,计算密集型应用的本地处理时延较高,无法满足垂直型业务的服务质量要求.除此之外,计算密集型应用由于在计算能力和时延方面要求较高,同时也会造成用户设备耗电量较大,极大缩短了用户设备的电池寿命.传统的解决方案是采用移动云计算技术(Mobile Clouding Computing,MCC),将用户设备任务卸载到资源丰富,数据存储量大的远程中央云服务器上在进行任务的处理后将结果反馈给用户设备,这虽然解决了用户设备对于计算能力的要求,但通过广域网的数据传输容出现成因数据交换而产生较长的时延以及数据丢失的情况.

近几年来,为了解决爆炸性的计算需求和日益增长的计算质量的设备需求,多接入边缘计算(Multi-Access Edge Computing,MEC)应运而生.多接入边缘计算是一种结合5G架构的技术,其目标是将云功能带到网络的边缘,通常部署在靠近接入点(Access Point,AP)或核心网络的某些聚合点.利用毫米波接入到邻近的移动边缘主机(Mobile Edge Host,MEH)上完成计算,存储和通信等操作,能够为移动用户设备提供更快的服务访问能力,提高计算体验的质量,包括能耗和执行时延[1-4].

当前如何定义对通信资源和计算资源的有效管理,保证较低的端到端的服务时延和较高可靠性有待深入研究.Pavel.等详细的介绍MEC功能集成到移动网络的现有概念,并讨论MEC标准化的当前进展,阐述计算卸载的研究主要分为3个关键领域,即计算卸载决策,MEC内的计算资源分配以及移动性管理三方面,并讨论尚未解决的研究挑战以及MEC存在的发展潜力[5,6].如何实现计算卸载中的资源分配问题是当前MEC所面对的一大挑战,同时也是过去几年该研究领域所研究的关键课题,并在各种MEC系统中广泛研究.

文献[7]关注在单用户设备的MEC系统中在时延的约束下最小化本地计算和任务卸载功耗问题.文献[8]将该网络场景扩展到多用户设备的MEC系统中,在特定应用程序的时延约束下,协同优化卸载决策选择,通过联合考虑无线电资源和计算资源分配从而解决化移动用户设备的功耗最小化问题,并定义该问题为混合整数非线性规划问题(Mixed Integer Nonlinear Programming,MINIP),基于分枝定界方法(Reformulation Linearization Technique Based Branch-and-Bound,RLTBB)的线性化技术和基尼系数的贪心启发式算法实现该凸问题的最优解或次优解.

在多用户设备MEC系统中,最优系统资源分配不仅与随机计算任务到达有关,而且与多个设备之间的竞争所产生的空间耦合有关.此外,并行本地和远程处理的自由度使得移动执行策略、计算卸载策略和在MEC服务器上的操作都相互影响着.因此,应考虑无线电资源和计算资源的智能联合分配,以最大限度地提高MEC的系统性能.文献[9]考虑基于频分多址(Frequency Division Multiple Access,FDMA)的多用户设备MEC系统中,随机联合无线电资源和计算资源管理,并引入李雅普诺夫随机优化理论技术(Lyapunov stochastic optimization)实现在任务缓冲区稳定性的约束下最小化移动设备和MEC服务器的平均加权功耗.文献[10]则分别考虑在基于时分多址(Time Division Multiple Access,TDMA)和正交频分多址(Orthogonal Frequency Multiple Access,OFDMA)的多用户设备MEC系统下,多移动设备在具有相同时延约束下的资源分配问题.文献[11]以用户设备为中心,考虑在用户设备长期平均功耗的约束下,最优化无线接入和计算所产生的时延,引入一个惩罚函数避免用户设备频繁切换和多臂赌博机(Multi-Armed Bandit Algorithm)算法以用户设备最佳关联.文献[12]在考虑在物联网场景下,设计一个基于随机梯度下降(Stochastic Gradient Descent,SGD)的在线计算算法使得物联网设备,边缘服务器和总服务延迟之间保持最优权衡.文献[13]对计算任务的功耗和时延很高要求的车联网领域在传统的粒子群算法基础上,提出粒子矩阵编码的方式,优化车辆的卸载决策和MEC的资源分配,解决车辆网络中动态卸载过程中的多约束优化问题.但随着深度强化学习(Deep Reinforcement Learning,DRL)在许多领域都取得巨大的成功,DRL由于对时变环境具有较强的认知性,在车辆网络中得到广泛的应用.文献[14]提出基于DRL的高效计算卸载策略,在降低任务失败率和时延方面达到很好的效果.上述的研究均考虑在较为经典的无线信道条件下的传输,但MEC的计算卸载效率极其的依赖于无线信道的条件,因为计算卸载需要在移动设备和MEC服务器之间进行有效的无线数据传输.随着5G技术的全面部署,利用高容量毫米波(mmWave)访问和移动边缘主机(MEH)的密集部署向结合的技术的到深入的研究,mmWave能够提供极宽的带宽极大的提高传输的效率[4].文献[15]研究了通过mmWave通信传输实现多移动用户设备与AP-MEH的匹配,以及通信资源和计算资源的联合分配问题,基于多对一的匹配理论和惩罚逐次凸逼近策略(Successive Convex Approximation,SCA)在减少时延和功耗的约束下为移动用户设备接入到AP-MEH上提供最优的策略.文献[16]将单AP和单MEH的网络场景扩展到多AP多MEH对的场景,提出由两个阶段组成的ODS-AO算法,在第1阶段实现最优卸载决策,第2阶段是实现资源分配的局部最优解的解决方案.文献[17]只考虑多AP和多MEH场景,在队列稳定性约束条件下,提出一种基于随机优化理论和匹配理论的在线算法,实现用户设备与计算资源和通信资源的最优动态资源分配.

从现有的研究来看,计算卸载中的资源分配在各个领域上都得到广泛的应用,其所运用的场景从单用户设备的MEC系统场景向多用户设备的MEC系统场景扩展研究较为广泛的多AP多MEH的场景.在不同的通信条件下和约束条件下的资源分配方案也得到了深入的研究.但由于当前的系统设计依赖于平均指标(例如平均队列长度和平均延迟),对时延约束条件下的资源分配方案还需进行深入研究.

时延约束下的动态计算卸载问题首次在文献[18]中提出,Liu.等对计算队列引入一个概率约束,并通过极值理论定义为超过一个确定值概率的边界,文献[19]则扩展到多AP多MEH的场景下,基于匹配理论引入一个用户设备分配策略.文献[20]为每个用户设备增加能量收集装置,在多用户设备的MEC系统下,考虑有限块长度和可靠性的约束,基于随机优化理论在服务时延和移动设备上能耗之间实现了最优平衡的策略,文献[21]考虑在平均时延和失效概率的约束下,将用户设备任务卸载到单个MEH上,联合优化在计算和通信资源分配.最终实现用户设备长期平均功耗.

综上所述,在时延约束下的资源分配方案的研究大部分主要是在单MEH的场景下,对于多AP和多MEH场景下的资源分配方案,大部分考虑在平均性能的约束下,不能满足于要求极高时延和可靠性的计算密集型应用.

基于上述的分析,本文针对基于mmWave接入的多AP和多MEH的边缘计算场景,解决在平均时延和失效概率的约束下最小化用户设备的长期平均功耗问题,并将该最小化问题定义为混合整数非线性规划问题.基于随机优化和匹配理论,提出了一种联合优化无线资源和计算资源的资源分配方案,在实现用户设备与AP-MEH关联后,实现通信资源和计算资源的最优分配.通过调用李雅普诺夫随机优化理论处理卸载请求,信道状态以及计算队列,同时引入惩罚函数减少用户设备频繁切换,通过定义上述最小化问题优化通信资源和计算资源.通过与在队列稳定性的约束条件下的资源分配方案,证明所提出的资源分配策略将有着更好的性能.

本文的主要贡献有以下:

1)构建通过mmWave接入的多AP和多MEH的场景下的边缘计算网络的动态计算卸载问题,这样更能有效缓解把所有用户设备的计算任务卸载到同一个MEH上所需要的计算能力以及用于等待计算过程所消耗的时延,从而是用户设备能提供更好的服务质量.

2)引入匹配理论和李雅普诺夫随机优化理论,分别实现了用户设备的关联以及关联后的通信资源和计算资源的最优化;引入一个惩罚函数,有效地减少了用户设备在关联过程中的频繁切换,提高整体的计算卸载性能.

3)基于平均时延和失效概率值的约束条件,提出一种以最小化用户设备长期平均功耗为目标的计算卸载策略,通过仿真实验证明所提出的策略具有很好的系统性能.

2 系统模型

本文主要考虑在多AP和多MEH的网络场景模型下,优化用户设备与移动边缘主机关联匹配以及在实现关联匹配后联合优化通信资源和计算资源的问题.考虑K个用户设备(k=1,2,3,…,K)和N个AP-MEH对(n=1,2,3,…,N)的网络场景,其中每个用户设备通过毫米波(mmWave)接入AP上,并将相应的计算任务卸载到与之相对应的MEH,如图1所示.

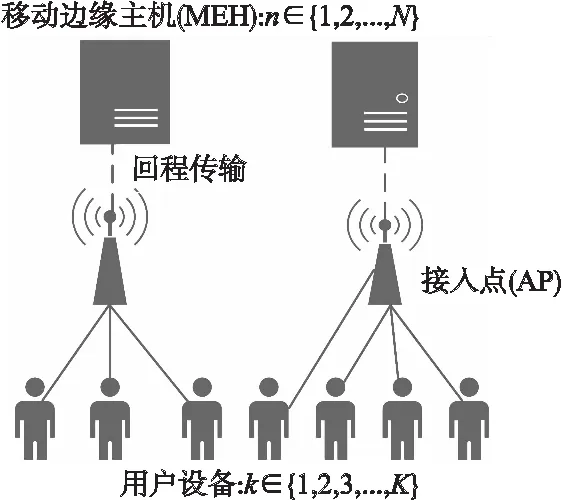
图1 网络场景

在动态的场景下,定义用于处理计算任务的时间为T,时间T被划分具为相等持续时间τ的时隙t,t∈{0,1,2…}.在时隙t内,定义akn(t)为当用户设备k与第n对AP-MEH对之间形成关联后的一个二进制变量,Sn(t)为在时隙t内用户设备分配到第n个AP的集合,则当用户设备k的卸载任务分配到第n对AP-MEH上时,可以通过以下公式表示为:

(1)

在时隙t内,用户设备端随机并持续生成计算任务,定义hkn(t)为用户设备k与AP-MEH之间的信道功率增益,在上行链路的传输过程中,定义pk(t)为链路的传输功率,βkn(t)为用户设备与MEH形成关联后,分配给用户设备k的带宽比例.在时隙t内,用户设备k的的最大传输速率为:

(2)

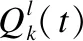
(3)

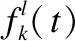
(4)

(5)

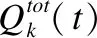
(6)

该动态分配问题用以下数学表达式进行表示:

s.t

(c)0≤pk(t)≤PK,∀k,t;

(d)0≤βkn(t)≤1,∀k,n,t;

(f)akn(t)∈{0,1},∀k,n,t;

(h)0≤fkn(t)≤Fn,∀n,t;

(7)

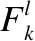
(8)

其中,σ是一个惩罚因子,引入惩罚函数的目的是减少该动态过程中的频繁切换的次数,因为在每个时隙内,用户设备与AP-MEH之间进行关联时,会导致分配变量的频繁切换,及用户设备在不同的AP-MEH对之间进行切换,找到最适合的匹配关联.这不仅增加了关联的复杂性,同时造成因从旧的AP-MEH到新的AP-MEH之间的状态转移而产生了额外的时延.

为了有效的定义式(7)中的(a)和(b)两个约束条件,我们引入两个虚拟队列.定义Zk(t)为每个用户设备的平均队列长度(即为平均时延),且该长度不超过一个预定义的值,该虚拟队列长度可以定义为:

(9)

上述引入的虚拟队列主要与(a)的约束条件相对应,约束条件(b)表达的含义为确保式(5)中总队列长度超过最大值的概率不超过预先定义的失效概率值,为了引入虚拟队列,引入一个指标函数1{·},通过以下等效的转换形式可以将约束条件(b)改写成以下表达式:

(10)

(11)

其中,u(·)为阶跃函数,定义虚拟队列Yk(t)对约束条件(b)进行描述,μ是一种用于加速算法收敛的步长,不会影响问题的本质.该虚拟队列可以表达为:

(12)

用户设备k通过引入虚拟队列Zk(t)和Yk(t),上述的约束条件可以被虚拟队列的平均速率稳定的约束条件所替代,可以通过以下表达式表示为:

(13)

(14)

3 问题描述与求解

为了解决上述的动态分配问题,使用文献[22]中的随机优化工具.在K个用户设备的环境下,定义两个虚拟队列长度的队列积压,定义一个李雅普诺夫(Lyapunov)函数为:

(15)

其中,Θ(t)=[Z(t),Y(t)],Z(t),Y(t)用向量进行表示,该向量中的元素表示在时隙t内所有用户设备的虚拟队列长度.一个时隙条件下的李雅普诺夫漂移函数表示为:

Δp(Θ(t))=E{L(Θ(t+1))-L(Θ(t))|Θ(t)}

(16)

式(16)定义的漂移函数可以导致虚拟队列的平均速率稳定性,但同时也会造成不必要的功耗.为了平衡虚拟队列的平均速率稳定性和用户设备的长期平均功耗,引入漂移加惩罚函数:

(17)

其中,V是一个控制参数,用于权衡功耗和队列长度的切换数目.根据文献[18]的引用,首先推导出该惩罚函数的上界,通过最小化在每个时隙内上界的瞬时值,最小化该上界问题表示为:

(18)

其中,C是一个正实数,式(18)中的u{·}可定义为:

(19)

联立式(18)和式(19),该动态问题的数学表达式为:

(20)

其中,Z为式(7)中的(a)～(g)的约束条件,该最优化问题可定义为求解每个时隙内的混合整型非线性规划问题.具体可分解为两部分,第1部分主要采用匹配理论将用户设备k与AP-MEH对n之间建立关联匹配,第2部分在形成关联匹配的基础上,将最优化资源以闭式解分配到相应的MEH上.

3.1 最优化通信与计算资源

(21)

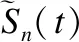
(22)

当用户设备将计算任务卸载到移动边缘主机上时,移动边缘主机分配用于处理计算任务的周期频率为fkn(t)=Fn.

3.2 用户设备关联匹配

为实现用户设备与AP-MEH对之间的相互关联,提出有着较低的复杂性和较高稳定性的基于大学招生问题的稳定广义匹配理论[23].该匹配理论涉及到两个集合,一个是用户设备集合,另一个是AP-MEH对集合.主要解决的是一个多对一的匹配问题,即一对AP-MEH可以和多个用户设备之间的产生关联匹配.但每个AP-MEH对可分配的的用户设备数是有限的.每个用户设备建立一个偏好函数用于对所有的AP-MEH对进行排序,即为Rk,n.相应的,AP-MEH对用户设备也有着偏好函数,即为Rn,k,偏好函数是基于用户设备的信噪比(SNR),且根据信噪比对用户设备进行降序排序.为了避免在分配过程中出现两个用户设备k1、k2分别分配到两个AP-MEH对n1、n2上,即相比于n2,k2更偏好于n1(即n1≻k2n2)或者AP-MEH对n1严格偏好k2多于k1,提出基于延迟接受算法(Deferred Acceptance,DA)的优化算法,其多项式复杂度能有效收敛到一个稳定匹配的状态.

在实现联合优化计算和通信资源之前,定义Gkn为用户设备与与接入点形成关联后式(20)的目标函数值,Gkn′为后续匹配过程中,用户设备k迁移到最新的MEH上所产生的新目标函数值.AP-MEH对可分配给用户设备的最大数量为qn,具体的联合优化通信资源和计算资源分配方案如下所示.

算法:联合优化通信资源和计算资源分配方案

输入:qn,Rk,n,Rn,k

输出:更新的稳定匹配Sn′目标函数值Gkn′

1.Fort=1:Nslotdo

2.ift=1do

运用延迟接受算法,得初始匹配Π0

根据式(21)、式(22)获得资源分配方案,并获得式(20)目标函数值Gkn

3.else

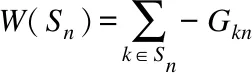
5.运用延迟接受算法,获得新的匹配

6.根据式(21)、式(22)得到资源分配方案,并获得新的目标函数值Gkn′

7.if|Gkn′|>|Gkn|

Sn→Sn′

|Sn′∪{k}|≤qn′

8.End

从上述算法分析可知,在用户设备与AP-MEH对之间关联方面,对已经进行初始匹配的用户设备在进行一次匹配优化,具体的匹配有方案为:第1个时隙内,每个用户设备只需根据自己的偏好函数实现用户设备与AP-MEH对之间关联,只需要满足每个MEH上所分配给用户设备的数量不超过最大数量即可.其他时隙内,用户设备在上述方案中的条件下建立新的偏好匹配函数,当新的偏好函数被执行时,用户设备k的接入状态从集合Sn转移到集合Sn′,且都不超过最大数量qn′.当两个用户设备都请求接入到同一个AP-MEH对上时,只考虑拥有最高信噪比的用户设备,当用户设备与AP-MEH对之间形成关联匹配后,会自动调用优化的计算资源和通信资源,并将两个最优化方案联合考虑,从而实现用户的长期平均功耗最小化.

4 仿真实验结果与分析

为了证明本文系统模型和策略的有效性,将本文提出的方案与在队列稳定性约束条件下的资分配方案进行性能对比分析.

4.1 仿真参数设置

在仿真实验中,本文考虑在多移动边缘主机和多用户设备场景下的计算卸载问题.该网络场景考虑10个用户设备在一个大小为150×150平方米的区域内随机移动,6个AP-MEH对在该区域内随机部署.每个用户设备通过最高的信噪比连接到AP,并将需要处理的计算任务卸载到与之相对应的MEH上,用户设备k与接入点n之间使用信道路径损失模型[24],相关的系统参数如表1所示.

表1 系统参数设置

此外,本文的目的是分析平均队列和失效概率的约束下最小化用户设备的长期平均功耗,因此,约束条件的参数如表2所示.

表2 约束条件参数设置

4.2 仿真实验与分析

本文通过MATLAB建立数值仿真实验,针对3.2节中提到在进行最优用户设备匹配时,会存在用户设备在不同的AP-MEH对之间进行切换以提高整体卸载的性能,但同时频繁切换的过程中会产生一定的时延损失.因此,当发生切换时,假设NtrNtr为应用程序状态从初始AP向目的AP迁移后所需要的时延,并在该时隙内,只能进行本地任务计算.本文将与考虑在队列稳定的约束条件下资源分配方法进行对比,证明所提出方法具有更好的增益.图2描述了平均用户队列长度和平均用户总功耗之间的关系,将平均任务到达率Aavg(t)设置为2Mbps,运行时间T=10000,通过对100组仿真实验结果进行总结分析,可得到该平均总队列长度(本地和远程队列之和)与用户设备平均总功耗之间的关系.

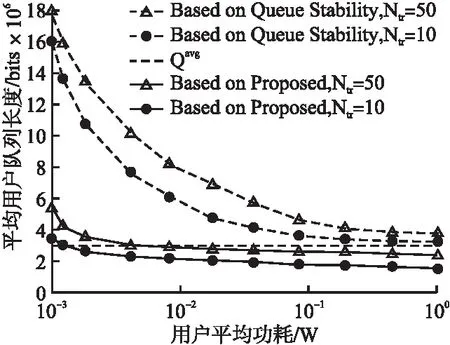
图2 平均功耗和平均队列长度的关系图

从图2可知,非负的李雅普诺夫权衡参数变量V与平均用户设备队列长度之间呈现反比,当V增加时,平均用户设备队列长度则不断减少,最后趋于平稳状态.相比于在队列稳定下的约束条件,本文所提出的方法平均用户队列长度随着用户功耗的增加,不断减少且在平均队列长度下,即在队列长度/功率权衡之间具有更好的效益;从图2也可知,Ntr越高,动态卸载的性能也越低,这是由于在用户设备切换发生后,迁移计算也需要消耗部分时延.但与在队列稳定下的资源分配方案相比,在平均时延和失效概率约束条件下的资源分配方法有着更好的性能.

为了更详细的分析在平均时延和失效概率的约束下有着更好的性能,接下来通过对约束条件的参数设置不同的变量,考虑在不同参数下的失效概率的变化.在图3中,考虑在V=4×1016以及平均执行时隙为T=3×105,考虑3个用户设备在不同的Qkavg,Qkmax,εk下的性能情况,分别设置用户设备的参数Qkmax=[15,25,35]×106,失效概率为εk=[10-1,10-2,10-3],k==1,2,3.为了说明失效概率的约束下的有效性,定义为1-CDF(Qktot)的可靠性函数.

图3 3个不同用户设备的总队列长度的概率变化

图3中的每条曲线表示Qktot(t)的概率大于横坐标上的值的概率,而不同的垂直虚线表示不同的用户设备所满足的最大队列长度.从图3结果可知,实线和虚线的交点表示Qktot和Qkmax之间的关系,通过导入式(11)对两者之间的关系进行分析,结果表明都满足所提出的失效概率的约束条件.

图4考虑了3个用户设备在每个时隙内的计算卸载的总队列长度的瞬时值的变化情况,每条曲线代表着每个用户设备在不同的时隙内的总队列长度瞬时值,虚线代表每个用户设备所需的最长队列长度,Qkmax,k=1,2,3.

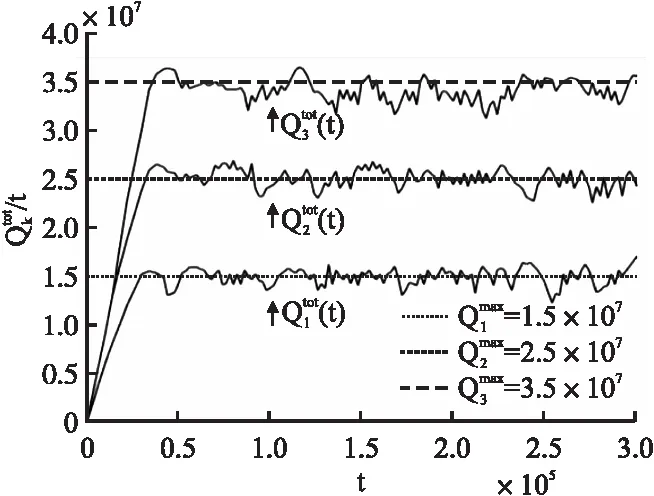
图4 3个用户设备的总队列长度瞬时值变化

从图4可知,基于失效概率约束下的计算卸载方案能有效确保用户需求所需的总队列长度的快速收敛,且不断收敛靠近每个用户的Qkmax.虽然在一些时隙内用户的总队列长度瞬时值超过用户的Qkmax,但从整体性能进行分析,基于失效概率约束条件下的资源分配方案将有着更好的性能.

本文所采用的计算卸载为部分卸载,即计算任务主要分为本地处理和远程处理.本文采用平均任务到达率Aavg(t)对整个动态任务卸载过程进行衡量,当设置不同的平均任务到达率对卸载过程的用户设备队列长度有着不同的影响.图5给出在不同的平均任务到达率的条件下,用户设备与平均总队列长度之间的关系.其中,横坐标表示用户设备的数量,纵坐标表示平均总队列长度.

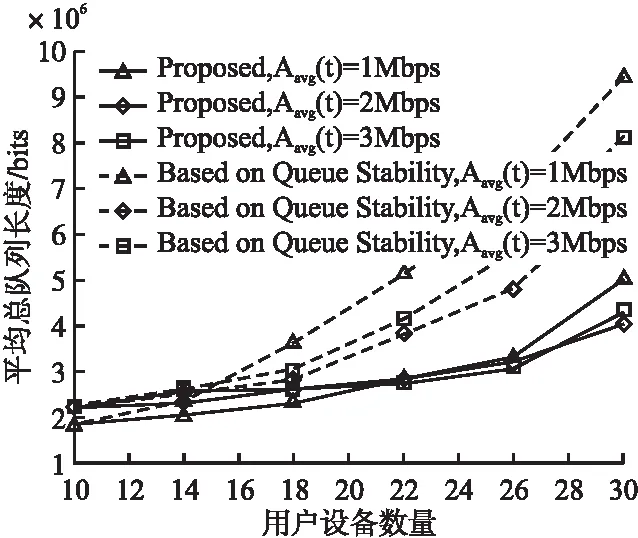
图5 平均总队列长度与用户设备数量的关系

从图5可知,随着用户设备数量的增加,需要进行卸载的计算任务也因此增加,但是在相同的任务到达率的条件下,本文方法比在队列稳定条件下的方法所需的时延更少,效益更好.在同一种方法下,设置不同的平均任务到达率参数,用于动态卸载所需要的时延也有所不同.

综上,本文提出的动态计算卸载方法相比于在队列稳定性约束条件下的资源分配策略有更好的性能和效益,能有效降低用户设备长期平均功耗.

5 总 结

本文主要研究在MEC下的动态联合无线资源和计算资源的计算卸载中的资源分配问题.考虑在平均时延和失效概率约束条件,最小化用户设备长期平均功耗问题.为了实现功耗与队列长度的最佳权衡,基于随机优化理论,引入一个在线算法框架用于处理系统的动态特性,引入匹配理论实现用户设备与移动边缘主机之间的相互关联.通过与队列稳定性约束下的计算卸载资源分配策略进行数值仿真实验对比,证明了所提出的方法对系统具有潜在的增益,能有效的降低总用户设备的长期平均功耗.