多AES分组杂凑模型原像攻击研究
李瑞同,刘 亚,2,赵逢禹
1(上海理工大学 光电信息与计算机工程学院 上海市现代化光学重点实验室,上海 200093)
2(中国科学院 信息工程研究所 信息安全国家重点实验室,北京 100093)
1 引 言
随着现代经济和技术的飞速发展,当代社会已悄然变成了一个信息化社会,各式各样的信息技术给人们的工作和生活带来了极大的舒适和便利,网络上的信息呈指数倍增长,如何保证这些信息的安全性变得越来越重要,而杂凑函数是现代密码学中保证信息完整性的重要工具.杂凑函数又称哈希函数,它将任意长度的消息压缩成固定长度的消息摘要,该消息摘要也被称为杂凑值.消息摘要可以看成每个消息的一个独特“数字指纹”,即使更改消息的一个数字或者字母,对应的消息摘要也会发生变化,从而保证了消息不被非法篡改[1].
杂凑函数需要满足3大安全性质:单向性、抗弱碰撞性和抗强碰撞性.在抗弱碰撞性和抗强碰撞性方面,2005年我国著名密码学家王小云教授已经证明经典的杂凑函数如MD4、MD5、SHA-0等存在碰撞[2,3].在单向性方面,研究者一般利用各种分析手段进行原像攻击找到杂凑函数的原像[4].若某一杂凑函数的原像可以被恢复,则敌手可以破坏数据的完整性,给现实系统带来巨大的危害.区块链中挖矿问题实际上就是针对特定杂凑函数求满足某种要求原像的过程.中间相遇攻击最早由Diffie等人于1977年提出的原像攻击中最常用的分析方法[5],它的主要思想是将杂凑函数对应的压缩算法分为两部分,一部分进行前向计算,另一部分进行后向计算,经给定杂凑值剪接后得到中间状态值,若两部分计算的中间状态值相等,则匹配成功,从而恢复出给定杂凑值对应的伪原像,最后再经过多次尝试恢复出原像.近年来,一些改进技术如连接与剪切、部分匹配、间接部分匹配和初始结构等陆续涌现出来有效地提高了基于中间相遇攻击的原像攻击的轮数和成功率[6,7].譬如:Shen Yanzhao等人提出了30轮SM3(我国杂凑函数标准)原像攻击[6],Li Ting等人分别提出了3轮KECCAK-224和4轮KECCAK-256原像攻击[8].
分组密码通过工作模型一直被广泛地运用到杂凑函数构造中,这类杂凑函数既可以被用在资源受限环境如基于标签的各类应用系统中保障信息的保密性和可认证性;也可以用于通常的杂凑函数的构造中.2008年美国国家标准与技术研究所(NIST)向全球公开征选第三代杂凑函数标准中许多候选算法是基于分组密码构造,其内部压缩函数采用高级加密标准AES(Advanced Encryption Standard)是比较普遍的构建,如Whirlpool、ECHO、GrØstl[9](SHA-3的最终5个候选算法之一)等.
采用AES的杂凑函数的安全性自提出以后就受到研究者的广泛关注,ECHO算法由Jérémy Jean等人在时间复杂度为2112次情况下实现了5轮的碰撞攻击[10],Whirlpool算法由Sasaki Yu在时间复杂度为2504次情况下实现了5轮的原像攻击[11],GrØstl-256和GrØstl-512算法由Wu Shuang等人在时间复杂度分别为2206和2495次情况下相应实现了5轮和8轮的原像攻击.
为了更深入地挖掘采用AES分组密码构造的杂凑函数更为本质的安全漏洞,采用AES构造的杂凑函数模型的研究一直以来受到了研究者的广泛关注.2011年,Sasaki Yu成功实现了7轮AES单分组杂凑模型的原像攻击的研究分析[11].2016年,Donghoon Chang等人也成功实现了10轮AES-128密钥策略杂凑模型的第二原像攻击分析[12].2019年,Guo Jian等人在此基础上又提出了8轮AES-192/256密钥策略杂凑模型的改进原像攻击研究分析[13],在此攻击中运用了AES-192/256的轮密钥关系.在SHA-3竞赛的候选算法中还有一个算法LANE[14]是采用了多个AES分组构造的杂凑函数.随着量子计算理论的发展,基于大分组分组密码构造杂凑函数的模型受到越来越多的关注.而对于利用分组密码构造的杂凑函数的安全性研究中,目前尚未有对压缩函数采用多个AES分组杂凑函数结构的安全性研究.这类压缩函数采用多AES分组的杂凑模型由于处理消息的规模更大,在后量子时代可能会被广泛运用.
压缩函数采用多个AES分组且通过工作模式构造的杂凑函数模型是指压缩函数采用多个AES分组构造,每一轮借鉴了AES的基本运算,采用了字节替换、行移位、列混淆和轮常数加操作.类似地,最后一轮省去列混淆运算.每一轮中间状态值运用一个线性变换更新为下一轮的中间状态值,特别地可以采用LANE算法的状态更新线性变换来更新每一轮的状态值.如图1所示.

图1 多AES分组的杂凑模型
本文利用连接与剪切技术、初始结构等技巧研究了基于多个AES分组通过DM模型的杂凑模型的安全性.具体来说,提出了对7轮双AES分组和6轮4个AES分组的杂凑函数模型的原像攻击,其中双AES分组的杂凑函数模型是指消息分成两个128比特,然后每轮字节替换、行移位、列混淆、轮常数加和LANE的状态更新线性变换;4个AES分组的杂凑函数模型采用类似的结构,不同之处仅在于将消息分成四个128比特分组.攻击基于7轮双AES分组的杂凑模型需要的时间复杂度和存储复杂度分别为2249次和218字节;攻击基于6轮4个AES分组的杂凑模型需要的时间复杂度和存储复杂度分别为2497次和235字节.与已有7轮单AES分组杂凑模型的原像攻击相比,双AES分组杂凑模型可以达到几乎相当的安全强度,而四AES分组杂凑模型安全强度更强.而这类杂凑函数模型的安全性的研究将是对利用分组密码构造杂凑函数设计理论的有力补充.此研究成果是对采用AES杂凑模型原像攻击的一个重要补充,为采用AES杂凑模型的杂凑函数设计提供了有力的理论保障.
2 预备知识
2.1 符号标记
在介绍算法之前,先列出符号标记,具体如下:
1)ki,ci,mi:分别表示第i轮的密钥,常数,消息块.
2)Hi:表示第i轮的链接变量值,当i为最后一轮时,则表示杂凑值.
3)CF():表示杂凑算法中的压缩函数.
4)Xi,Yi,Zi,Wi,Ui:分别表示第i轮字节替换、行移位、列混淆、轮常数加和多分组交换之前的中间状态值.
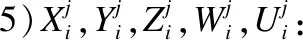
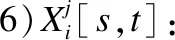
7)IV:表示初始链接值.
8)H():表示杂凑函数.
2.2 多分组加密的杂凑模型描述
PGV模式是常用的通过分组密码构造成杂凑函数的工作模式,譬如MD5、SHA-2和SHA-3竞赛中候选算法GrØstl等.而PGV模式在实际中被广泛运用的3种模式分别为DM,MMO和MP模式[15].具体如下:
其中Ek()表示以密钥k进行加密操作.
本文研究的多分组AES加密的杂凑函数结构采用DM模式,内部压缩函数的轮函数Ek()借用了AES算法的构造,内部状态首先分成若干个128比特的分组,每128比特表示为4×4字节矩阵,内部状态每轮的轮函数迭代执行,主要包含下面5个操作:
1)字节代换(SubBytes,SB):每个字节经过非线性S盒运算后,完成替换操作.
2)行变换(ShiftRows,SR):每个字节数组中的第i行所有字节相应向左移位i个字节.(i=0,1,2,3)
3)列混淆(MixColumns,MC):每个字节数组的每一列左乘一个矩阵M,解密时即其逆过程时左乘M′,即可完成每一列字节的更新变换.
(这里的x表示十六进制数)
4)异或常数(AddConstants,AC):每个字节与对应的轮常数进行异或操作,在AES中这里一般异或一个固定轮密钥,这里即视为异或一个常数.
5)多分组交换(SwapCordsets,SC):在完成上述SB、SR、MC和AC操作以后,每轮内部状态值经过线性变换更新为新一轮的内部状态值.特别地,这个线性变换可以参考LANE的多列交换操作,具体对于两分组和四分组多列交换过程如图2和图3所示.

图2 两分组多列交换图
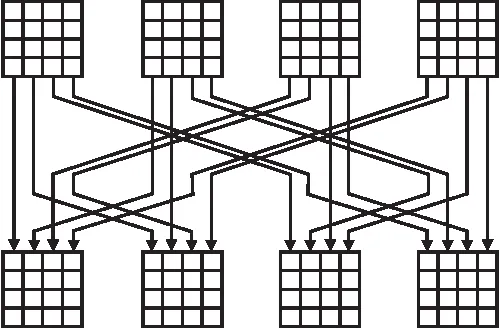
图3 四分组多列交换图
为方便描述攻击过程,每一个分组中字节的位置按列优先顺序排列,第1列依次为0,1,2,3,第2列依次为4,5,6,7,第3列依次为8,9,10,11,第4列依次为12,13,14,15.
2.3 原像攻击安全性分析方法简介
近年来,中间相遇攻击及其改进技巧在原像攻击中起到了越来越重要的作用,下面将简要阐述中间相遇的原像攻击思想及其改进技巧.
在针对杂凑函数执行中间相遇攻击时,其主要思想是将消息扩充分成相互独立的两部分,分别寻找两部分的中性字,然后从两个方向计算,一部分执行向前的独立计算,另一部分执行向后的独立计算.若有一个消息ma值的变化完全不影响后向计算,就可以称ma为后向消息块的中性字,那么根据不同的ma的值进行前向计算,即可在匹配处产生一个数据集合,可以将其存储在表L中;同理,若mb的值变化完全不影响前向计算,那么mb就是前向消息块的中性字,每次取一个不同的mb值进行后向计算,对应在匹配处也会产生计算结果,可以将每个后向计算产生的结果和表L中前向计算的值进行匹配,直到找到完全匹配的项为止[11].一旦产生一个匹配对,即找到了对应的伪原像.
近年来,随着中间相遇攻击技术的逐步发展,各种改进技术也渐渐被发掘出来,并且成功地应用在各类算法的分析中[16-18],这里简单介绍本次改进中间相遇攻击过程中用到的几个改进技术.
1)连接与剪切(Split-and-cut)
在原像攻击定义中,杂凑值是给定的,如果压缩函数采用DM模式,那么初始链接变量值就等于给定的杂凑值减去最后的链接变量值,从而可以把初始链接变量与最后的链接变量连接在一起,使得中间所有的链接变量都能成为起始点,这样就能在更大的消息空间中搜索中性字、分隔前后向的消息块,因而大大提高中间相遇攻击的成功率.
2)初始结构(Initial-Structure)
中间相遇攻击中,两个独立消息块的中性字在攻击开始的位置可能会混合在一起,因此很难找到合适的相互独立的消息块.初始结构技术就被用来解决这个问题,有助于找到更好的两个相互独立的消息块,来进行更成功的中间相遇攻击.
3)部分匹配(Partial-Match)
部分匹配[3]是为了加快匹配成功的效率,会对两块消息字的部分特定字节进行优先匹配,继而进行全部匹配,从而大大提高攻击的轮数.
4)间接部分匹配(Indirect Partial-Match)
间接部分匹配技术是部分匹配技术的扩展.将匹配点的计算能够分解成以前后向消息块的中性字ma和mb为变量的函数独立计算,经过变换后使得对应前后向块的中性字出现在了同侧,如此前向计算和后向计算均可顺利执行,这样就可以执行间接部分匹配[19].
结合了以上这些改进技术的中间相遇攻击过程示意图如图4所示.

图4 改进中间相遇攻击示意图
5)伪原像转换为原像
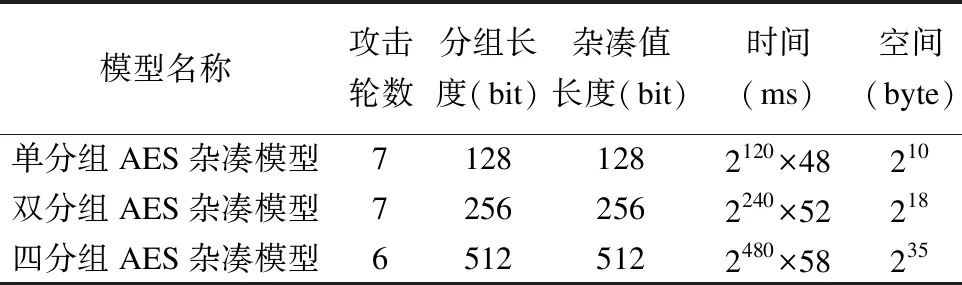
伪原像是指给定杂凑值Hi+1,如果找到(Hi,Mi),使得Hi+1=CF(Hi,Mi)成立,那么(Hi,Mi)就可以称为是压缩函数CF()的一个伪原像.伪原像的形成原因是因为它的初始链接值不是正确的初始向量IV.因此需要计算一个消息块的杂凑值来连接指定初始链接值到伪原像的初始链接值.可以利用生日攻击的思想来寻找这个合适的消息块,假如找到一个n位杂凑值的迭代杂凑函数的伪原像需要的代价是2k,则其找到对应一个原像的代价即为2[(n+k)/2]+1.当k 图5 双AES分组杂凑模型的改进中间相遇攻击 (1) (2) (3) (4) (5) 进一步还可以将公式(5)转换为如下的公式(6): (6) 对于公式(6),令: (7) 同样地,令: (8) 因此通过计算每一块的Cfor,Cback,C′for和C′back进行匹配. 如图5所示,整个攻击过程可描述为: (c)将Cfor和C′for的值存储在两个表Tfor和T′for中. 3)在得到216个值后对表Tfor和T′for进行分类存储. (d)检查表Tfor和T′for中是否有条目对应匹配Cback和C′back. (e)一旦存在匹配,就根据已匹配的值计算出全部的32字节的值,并检查是否全部32字节的值全部匹配. (f)一旦全部的32个字节全部匹配,即可输出对应的(HN-1,MN-1),至此即可找到一个伪原像. 在步骤2)的(c)中,需要216×4=218字节来存储Cfor和C′for. 最终7轮的伪原像和原像改进攻击时间复杂度分别是2240和2249次.存储复杂度是218字节. 为进一步研究发动攻击的计算开销,现在一台Windows10,CPU2.40 GHz,编程环境为Python3.2的个人电脑上执行上述攻击过程,攻击算法流程可描述为算法1. 算法1.双分组原像攻击算法 输出:给定杂凑值H的伪原像 1.fori=1to2Hdo: 3. 定义一个存储空间为218字节的空列表List[]; 6. List[]←Cfor,C′for 7.endfor 10.endfor 11.ifCback,C′backinList[]isTRUE 12. 计算并输出该中性字对应的分组,此分组即为给定杂凑值H的原像 13.elsei=i+1;//重新固定初始结构中除中性字外其他字节值,再次执行 14.endif 15.endfor 经过实验验证,执行216次循环需耗时55min,得出执行原像攻击过程中一次循环大约耗费的平均时间约为52ms,预计需要耗费2240×52ms即可成功恢复7轮双AES分组杂凑模型的伪原像,所需存储空间为218字节. 在双AES分组的杂凑模型的改进中间相遇攻击的基础上,进一步提出6轮四分组杂凑模型的改进中间相遇攻击. 针对6轮四AES分组的杂凑模型的原像攻击过程如图6 图6 4AES分组杂凑模型的改进中间相遇攻击 (9) (10) 进一步还可以将公式(10)转换为公式(11): (11) 对于公式(11),同理可令其为公式(12): xb·D0⊕xe·D1=Dback xb·D2⊕xd·D3=D′back xb·D6⊕xd·D7=D″′back (12) 如图6所示,整个攻击过程可描述为: (e)一旦存在匹配,就根据已匹配的值计算出全部的64字节的值,并检查是否全部64字节的值全部匹配. (f)一旦全部的64个字节全部匹配,即可输出对应的(HN-1,MN-1),至此即可找到一个伪原像. 最终6轮的伪原像和原像改进攻击时间复杂度分别是2480和2497次,存储复杂度是235字节. 为进一步研究发动攻击的计算开销,在与3.4节同样环境的个人电脑上执行上述攻击过程,其攻击流程与算法1类似,经过实验验证,执行216次循环需耗时68min,得出执行原像攻击过程中一次循环大约耗费的平均时间约为58ms,预计需要耗费2480×58ms即可成功恢复6轮四AES分组杂凑模型的伪原像,所需存储空间为235字节. 本文主要研究了多AES分组的杂凑模型的安全性分析.首先分析了多AES分组加密的杂凑模型的加密过程.接着在基础的中间相遇攻击技术的分析之上,引入一系列改进技术,如初始结构、部分匹配和间接部分匹配等,在保持一定的时间复杂度和存储复杂度情况下,成功实现了7轮基于双AES分组的杂凑模型的改进中间相遇攻击,整个伪原像攻击的时间复杂度为216×2224=2240次,存储复杂度为218字节.在此方法基础上,进一步实现了6轮基于4个AES分组的杂凑模型的改进中间相遇攻击,整个伪原像攻击的时间复杂度为232×2448=2480次,存储复杂度为235字节.在一台Windows10,CPU2.40 GHz,编程环境为Python3.2的个人电脑上进行实验验证,传统单AES分组的杂凑模型和本文提出的多AES分组的杂凑模型在相同计算环境下进行伪原像恢复预计使用时间和空间的开销如表1所示. 表1 单AES分组和多AES分组杂凑模型伪原像攻击对比 从表1可得原像恢复的计算时间和存储空间开销与AES分组数成正比.这也是首次利用中间相遇技术对多AES分组的杂凑模型的进行抗原像攻击安全性分析.研究结果表明:当杂凑函数的压缩函数至少采用8轮双AES分组或7轮四AES分组时,才能分别保障双AES分组或四AES分组的杂凑函数能够有效地抵抗抗原像恢复的安全性分析.此结果是对双AES分组和四AES分组杂凑函数模型设计理论的一个重要补充.3 7轮双AES分组杂凑模型的改进中间相遇攻击
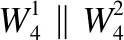

3.1 初始结构
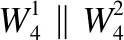
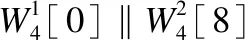


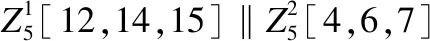
3.2 匹配过程
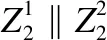
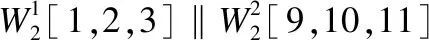
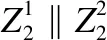
3.3 攻击过程
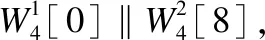



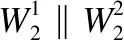
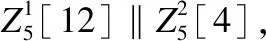
3.4 复杂度分析
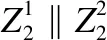
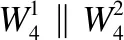


4 6轮四AES分组杂凑模型的改进中间相遇攻击

4.1 初始结构

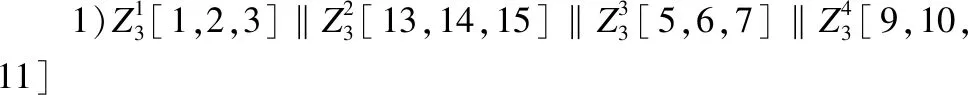

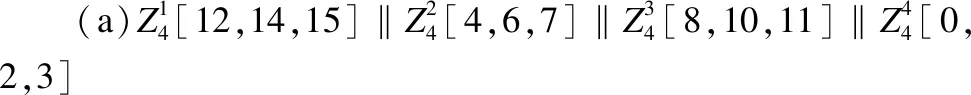


4.2 匹配过程

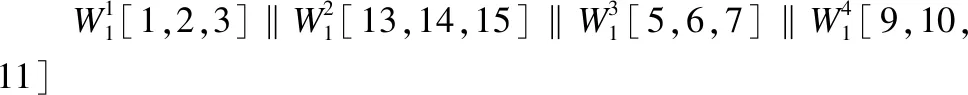

4.3 攻击过程


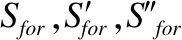



4.4 复杂度分析


5 结 语