典型可燃气体小孔泄漏危险范围预测模型研究

赵开功 ，张晓蕾 ，李长明 ，陈 刚 ，盖泳伶

（1.北京科技大学 土木与资源工程学院, 北京 100083；2.国家能源投资集团有限责任公司 安全环保监察部, 北京 100011；3.中国安全生产科学研究院, 北京 100012；4.中国矿业大学(北京) 应急管理与安全工程学院, 北京 100083；5.国能网信科技(北京)有限公司, 北京 100011；6.中国人民解放军63600 部队, 甘肃 酒泉 732750）

0 引 言

能源是国家的重要基础产业，能源安全是国家安全的重要组成部分[1-3]，我国是一个缺油、少气，煤炭资源相对丰富的国家[4]，随着时代的发展和国民经济的高速增长，石油消费增速远大于国内石油资源增产的速度，发展合成油工业作为石油资源的补充是合理的[5]。各种化工合成工艺所用原料气的有效成分主要是H2、CO 和CH4，而在各种工艺中，大多数都需要在高压环境中进行，如合成油品所需压力为2～3 MPa，合成二甲醚则需要2～4 MPa 压力[6]，因此合成装置、运输管道一旦发生泄漏，造成人员及经济损失不可估量。

数值模拟能够表示参数的变化关系，使用数值计算方法进行求解，能够得到过程中的动态模拟结果，极大地促进了科学研究的发展。刘彦青[7]在同时考虑瓦斯含量与压力的情况下，通过数值模拟方法计算得到了使煤层瓦斯涌出量最低的工作面平均推进速度周期为25～30 d。在高压气体泄漏扩散的研究中，李伟等[8]通过流体力学计算软件，对于高压甲烷储罐的泄漏喷射和扩散过程进行了数值模拟，通过数值模拟结果，建立了甲烷容器内压力与破裂口喷射速度的定量公式。在甲烷高压球罐的泄漏研究中，傅杰[9]利用Fluent 软件，建立了较为准确的高压气体泄漏扩散的数值模型，并利用该模型探究了甲烷在不同泄漏条件下泄漏口附近以及气体泄漏远端的气体浓度、压力等物理参数的规律。刘延雷等[10]，通过数值模拟研究了管道内高压氢气、天然气的不同扩散特性，发现高压的氢气泄漏时产生的危险气体云团较大，且高压氢气泄漏时初始的泄漏速度远大于高压天然气泄漏时的初始速度，在地面附近区域氢气泄漏扩散产生的危险要小于天然气。同样是在天然气管道气体泄漏的研究中，周伟国等[11]通过数值模拟，对管道发生泄漏后泄漏压力、环境风速对于甲烷气体的扩散特性影响进行了研究，结果表明，管道内压力越大时，泄漏口气体速度越大，气体扩散范围也越大，当环境风速越大时，甲烷气体射流的偏转角度越大，扩散速率也越大。高嵩等[12]，利用Fluent 软件研究了高压天然气管道泄漏及其规律，通过建立的天然气长管道运输模型，对不同条件下管道泄漏的压力、浓度、速度及危险区域进行了分析，根据结果对比分析了不同泄漏孔径、不同泄漏压力对于气体泄漏范围的影响。徐坤等[13]利用Fluent 软件模拟了在机械通风条件下不同泄漏口方向、位置、泄漏压力等条件下燃气浓度分布特性，发现泄漏口的方向对于甲烷气体泄漏初期的浓度分布具有重大影响。刘敏鸿等[14]利用数值模拟方法，分别研究了天然气在封闭和半封闭小空间内的泄漏扩散规律，发现天然气在封闭空间泄漏发生爆炸的风险小于半封闭空间。袁裕鹏等[15]利用Fluent 软件，对不同泄漏条件下，氢气燃料电池仓内氢气泄漏扩散规律进行了探究，并发现氢气探测报警器适宜安装到空间顶部角落。汪建平等[16]采用数值模拟的方法，研究了天然气在厨房内泄漏扩散过程，并且将实验与数值模拟结果进行对比，验证了数值模拟的准确性。万宇飞等[17]利用Fluent 软件，研究了不同风向条件对于高压LPG 球形储罐中丙烷泄漏扩散规律的影响，可为发生泄漏时人员自救及消防救援提供参考。朱静等[18]采用数值模拟方法，模拟了天然气在典型住宅内泄漏扩散规律及自然通风对气体扩散的影响，结果表明自然通风可以很好地防止天然气聚集，降低爆炸风险。喻健良等[19]通过构建高压CO2管道泄漏扩散数值模型并根据实验结果进行验证，总结出不同大小泄漏孔下CO2浓度和温度分布规律。周宁等[20]利用Fluent 软件，研究了环境温度对于LNG泄漏扩散规律的影响，发现环境温度较高时，甲烷扩散最远距离大于环境温度低时。程方明等[21]利用FLACS 软件，对储罐内高压天然气非恒定速率泄漏进行了模拟，研究发现风速越大，气体泄漏扩散产生的气云稳定所需的时间越长。陶婧莹等[22]采用数值模拟的方法，利用高斯烟羽模型对LNG 泄漏扩散进行研究，发现在泄漏过程中，随着环境风速的增加，危险区域减小；随着大气稳定度的增加，危险区域增加。周宁等[23]利用Fluent 软件，对于不同条件下管道内丁烷气体泄漏扩散规律进行了研究，发现气体初始速度越大，自由扩散作用越强，危险范围也越广。张晓蕾等[24]采用PHAST 模拟软件，研究了不同工况下风速大小对周围建筑物及人员的热辐射影响，研究发现风速越大，热辐射影响的范围越大。

在上述对于高压气体泄漏的研究中可以发现，由于高压气体泄漏实验危险性较大，实验成本较高，因此许多研究采取了数值模拟的方法，且模拟结果可靠，在之前的大多数研究中，目标气体大多数集中在甲烷和天然气，对于化工合成中常见的气体，如H2、CO、CH4在不同泄漏条件下，泄漏规律及危险范围的研究并不充分，且通常轻视小尺寸泄漏口的危险性，因此开展常见可燃气体小孔泄漏扩散研究是十分必要的。

1 不同条件下可燃气体泄漏扩散规律及泄漏危险范围

1.1 CFD 数值模拟参数设置

本次数值模拟选择CFD 数值模拟方法，CFD（Computational Fluid Dynamics）全称为计算流体动力学，是通过计算机模拟流体的特定情境以得到流体相关参数并进行研究。选用ICEM 软件进行建模及网格划分，Fluent 软件进行高压气体泄漏的模拟，CFD-POST 软件进行数据后处理。在模拟过程中，求解器选择压力基求解器Pressure-Based，湍流模型选择考虑可压性影响的双方程k-omega SST 模型，该模型是一种在工程上得到广泛应用的混合模型，即在近壁面保留了原始k-ω模型，在远离壁面的位置应用了k-ε模型[25]，其方程与模型具体如下：

可压缩流体质量、动量、能量和组分守恒方程[26]可表示为

式中：ρ为密度；x为空间坐标；u为速度分量；g为重力加速度；E为总能量；cp为混合物在恒压下的比热容；Pr为普朗特数；T为温度；h为焓；Sc为进度变量守恒方程中的源项；Y为质量分数；R为火焰前锋平均半径；H为燃烧热。上标和下标中，上标：-为LES过滤后的量，～为LES 质量加权过滤后的量；下标：i，j，k为空间坐标索引；m为气体混合的第m个组分；c为源项在进行变量方程；eff 为有效值。

k方程和ω方程分别是：

其中：k为湍流动能；ω为湍流动能的特定消散，它们分别定义为

其中，ε为湍流动能消散率：

其中，τij为雷诺应力：

式中：t为时间；p为动力压强；μt为涡动黏性；δij为克罗内克函数；vT=μt/ρ为动力涡黏性；σk，β*，σω，γ，β，为模型系数；F1为混合函数[27]。

组分输运共涉及3 种气体，分别为H2、CO 和CH4，气体密度均为理想气体，时间属性选择定常流动（稳态）。本次CFD 数值模拟计算域的边界条件如图1 所示。

图1 计算域及其边界条件Fig.1 Computational domains and boundary conditions

本次CFD 数值模拟网格独立性检验共选择3种网格尺寸，其网格数量分别为101 850（high）、71 604（medium）、46 350（low），泄漏气体为H2，泄漏口直径为3 mm，泄漏压力为1 MPa，气体温度为300 K。图2 表示的是中心轴线H2浓度分布曲线，可见选用中质量网格（medium）得到的结果与高质量网格（high）十分接近。因此在考虑时间成本并保证结果准确的前提下，本次CFD 数值模拟采用中质量（medium）网格开展相关研究。

图2 3 组网格中心轴线处H2 浓度分布Fig.2 H2 concentration distribution at the central axis of the three groups

1.2 不同条件下可燃气体泄漏扩散规律及泄漏危险范围

如前文所述，CFD 数值模拟共涉及3 种气体，分别为：H2、CO 和CH4。对于3 种气体，其危险浓度即为爆炸极限，H2：4%～75%，CO：12.4%～75%，CH4：4.9%～16%。

CFD 数值模拟共设置81 组工况，泄漏气体分别为H2、CO 和CH4，泄漏口直径分别为2、3、4 mm，合成油品中低温F-T 合成所需压力2～3 MPa[3]，温度280 ℃以下，因此工况中，泄漏压力选定为1、2、3 MPa，气体泄漏温度为300、400、500 K。

1.2.1 不同泄漏压力下可燃气体泄漏扩散规律及泄漏危险范围

通过对H2、CO 和CH4三种气体在不同泄漏压力下气体泄漏浓度分布云图进行对比（图3），可以发现：

图3 不同泄漏压力下可燃气体扩散规律及泄漏危险范围Fig.3 Diffusion mechanism and danger range of combustible gas leakage under different leakage pressure

1）3 种气体在温度、直径等其他因素不变的条件下，随着泄漏压力的增大，气体泄漏危险范围随之明显增加，其危险范围除轴向长度增长之外，宽度也有所增大。

2）对于不同气体，压力同为1 MPa 时，H2泄漏的危险范围长度与宽度分别为2.36 m 和0.316 m，CO与CH4则仅为0.23、0.028 m 和0.67、0.09 m，可见H2的泄漏危险范围最大；当泄漏压力从1 MPa 上升到2 MPa 时，H2泄漏危险范围长度和宽度分别增加了11%和13%，而CO 泄漏危险范围长、宽分别增加了17%和11%，CH4则分别增加了9%和7%，可见H2、CO 和CH4三种气体泄漏危险范围均受到气体温度的显著影响。

从图4—图6 可以看出，泄漏压力越大，中心轴线浓度越高，如H2在泄漏压力1 MPa，泄漏口直径4 mm，泄漏温度300 K 时，距泄漏口0.3 m 处，体积分数为33%，而当泄漏压力为2 MPa 时，同样位置的H2体积分数则升高到38%。

图4 不同泄漏压力下中心轴线H2 浓度分布曲线（4 mm-300 K）Fig.4 H2 concentration distribution of center axis under different leakage pressure (4 mm-300 K)

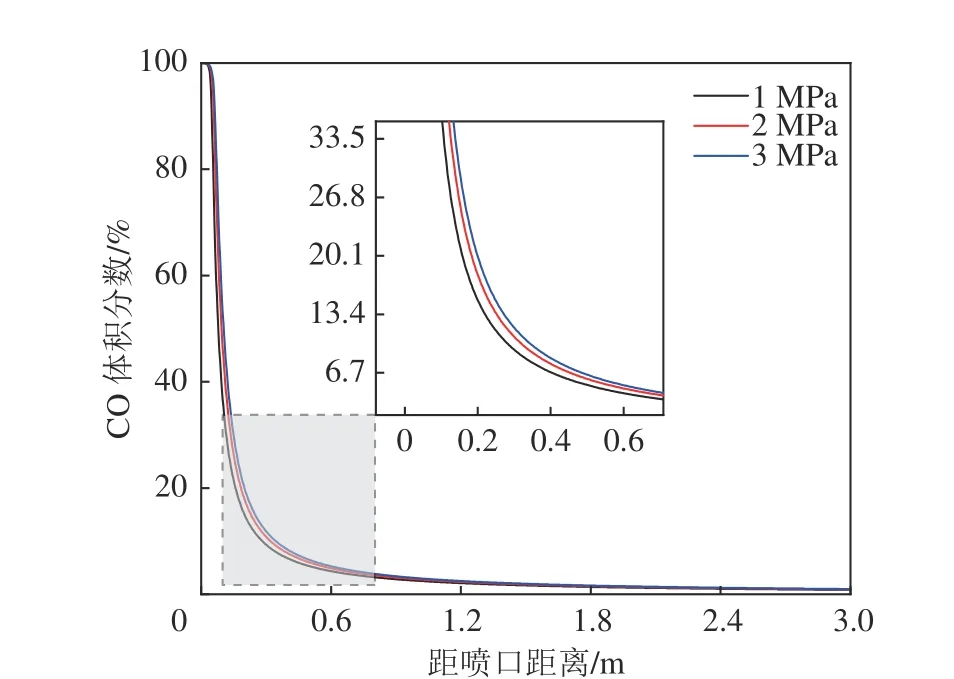
图5 不同泄漏压力下中心轴线CO 浓度分布曲线（4 mm-300 K）Fig.5 CO concentration distribution of center axis under different leakage pressure (4 mm-300 K)

图6 不同泄漏压力下中心轴线CH4 浓度分布曲线（4 mm-300 K）Fig.6 CH4 concentration distribution of center axis under different leakage pressure (4 mm-300 K)

1.2.2 不同气体温度下可燃气体泄漏扩散规律及泄漏危险范围

通过对H2、CO 和CH4三种气体在不同泄漏温度下气体泄漏浓度分布云图进行对比（图7），可以发现：

图7 不同泄漏温度下可燃气体扩散规律及泄漏危险范围Fig.7 Diffusion mechanism and danger range of combustible gas leakage under different leakage temperature

1）3 种气体在泄漏压力、直径等其他因素不变的条件下，随着气体温度的增大，气体泄漏危险范围随之明显降低，其危险范围除轴向长度减小之外，宽度也有所减小。

2）对于不同气体，温度同为300 K 时，H2泄漏的危险范围长度与宽度分别为2.04 m 和0.28 m，CO与CH4则仅为0.24，0.024 和0.62，0.074 m，可见H2的泄漏危险范围最大；当泄漏温度从300 K 上升到400 K 时，H2泄漏危险范围长度和宽度分别降低了11%和12%，而CO 泄漏危险范围长、宽分别降低了4.2%和12.5%，CH4则分别降低了10%和14%。可见H2、CO 和CH4三种气体泄漏危险范围均受到气体温度的显著影响。

从图8-图10 可以看出，气体温度越高，中心轴线浓度越低，如H2在泄漏温度为300 K，泄漏口直径3 mm，泄漏压力3 MPa 时，距泄漏口0.3 m 处，体积分数为37%，而当泄漏温度变为400 K 时，同样位置的H2体积分数为34%。从图8-图10 可以看出，气体温度越高，中心轴线浓度越低，如H2在泄漏温度为300 K，泄漏口直径3 mm，泄漏压力3 MPa 时，距泄漏口0.3 m 处，体积分数为37%，而当泄漏温度变为400 K 时，同样位置的H2体积分数为34%。

图8 不同气体温度下中心轴线H2 浓度分布曲线（3 mm-3 MPa）Fig.8 H2 concentration distribution of center axis under different leakage temperature (3 mm-3 MPa)

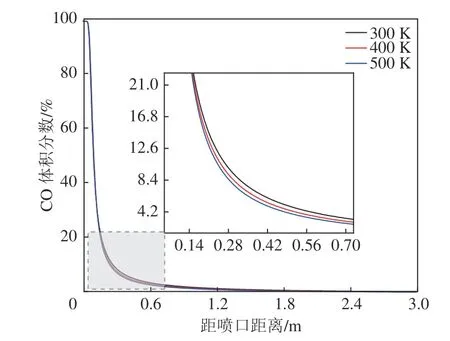
图9 不同气体温度下中心轴线CO 浓度分布曲线（3 mm-3 MPa）Fig.9 CO concentration distribution of center axis under different leakage temperature (3 mm-3 MPa)

图10 不同气体温度下中心轴线CH4 浓度分布曲线（3 mm-3 MPa）Fig.10 CH4 concentration distribution of center axis under different leakage temperature (3 mm-3 MPa)

1.2.3 不同泄漏口直径下可燃气体泄漏扩散规律及泄漏危险范围

通过对H2、CO 和CH4三种气体在不同泄漏口直径下气体泄漏浓度分布云图进行对比（图11），可以发现：

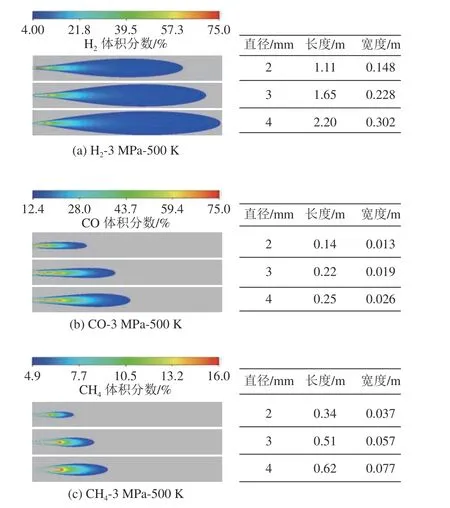
图11 不同泄漏口直径下可燃气体泄漏扩散规律及泄漏危险范围Fig.11 Diffusion mechanism and danger range of combustible gas leakage under different diameter of leak hole

1）3 种气体在温度、泄漏压力等其他因素不变的条件下，随着泄漏口直径的增大，气体泄漏危险范围随之明显增加，其危险范围除轴向长度增长之外，宽度也有所增大。

2）对于不同气体，直径为2 mm 时，H2泄漏的危险范围长度与宽度分别为1.11 m 和0.148 m，CO 与CH4则仅为0.14 m，0.013 m 和0.62 m，0.037 m，可见H2的泄漏危险范围最大；当泄漏口直径从2 mm上升到3 mm 时，H2泄漏危险范围长度和宽度分别增加了49%和54%，而CO 泄漏危险范围长、宽分别增加了57%和46%，CH4则分别增加了50%和54%。可见H2、CO 和CH4三种气体泄漏危险范围均受到泄漏口直径的显著影响。

从图12—图14 可以看出，泄漏口直径越大，中心轴线浓度越高，如H2在泄漏口2 mm，泄漏温度500 K，泄漏压力3 MPa 时，距泄漏口0.3 m 处，浓度为19%，而当泄漏口直径变为3 mm 时，同样位置的H2浓度为33%。

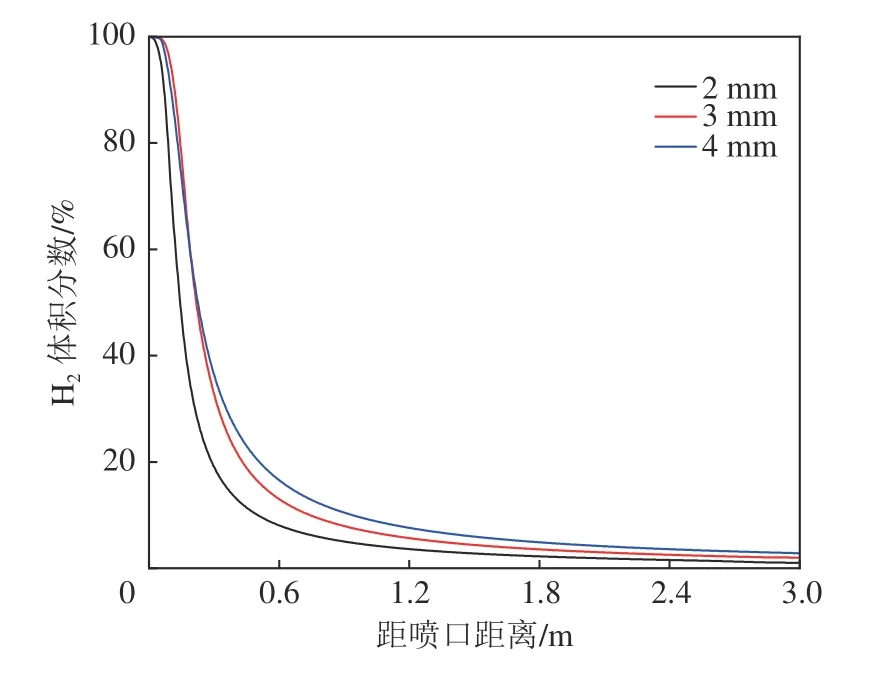
图12 不同泄漏直径下中心轴线H2 浓度分布曲线（500 K-3 MPa）Fig.12 H2 concentration distribution of center axis under different diameter of leak hole (500 K-3 MPa)

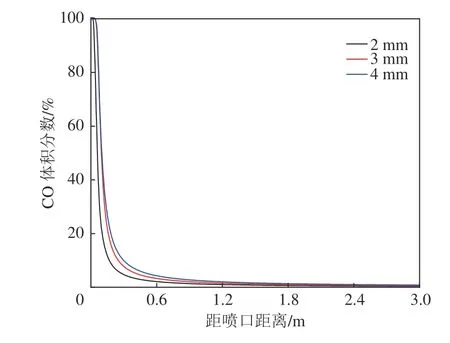
图13 不同泄漏直径下中心轴线CO 浓度分布曲线（500 K-3 MPa）Fig.13 CO concentration distribution of center axis under different diameter of leak hole (500 K-3 MPa)

图14 不同泄漏直径下中心轴线CH4 浓度分布曲线（500 K-3 MPa）Fig.14 CH4 concentration distribution of center axis under different diameter of leak hole (500 K-3 MPa)

2 可燃气体泄漏危险范围预测模型

本次CFD 数值模拟共考虑3 种气体，分别为H2，CO 和CH4，并充分考虑泄漏口大小、泄漏压力和泄漏温度后，根据得到的危险范围，对每种泄漏气体危险范围的长和宽分别进行拟合，得出泄漏危险范围定量预测经验公式（图15-图20）。对参量进行无量纲处理，得到的泄漏危险范围定量预测模型为：

图15 H2 泄漏危险范围长度经验公式Fig.15 Empirical formula of the length of H2 leakage danger range

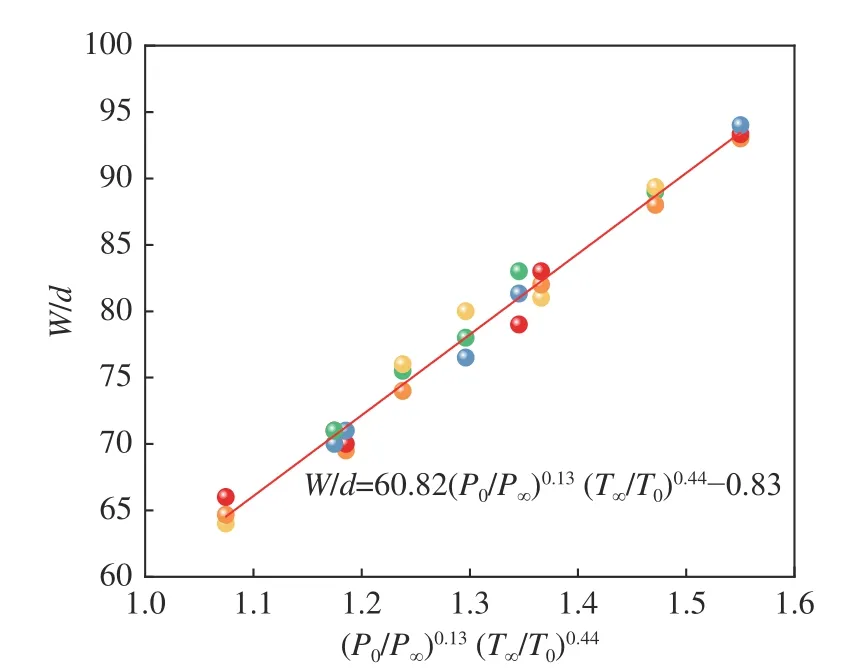
图16 H2 泄漏危险范围宽度经验公式Fig.16 Empirical formula of the width of H2 leakage danger range

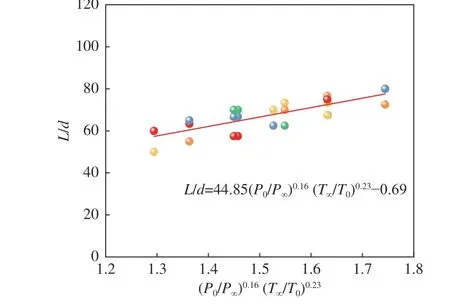
图17 CO 泄漏危险范围长度经验公式Fig.17 Empirical formula of the length of CO leakage danger range

图18 CO 泄漏危险范围宽度经验公式Fig.18 Empirical formula of the width of CO leakage danger range

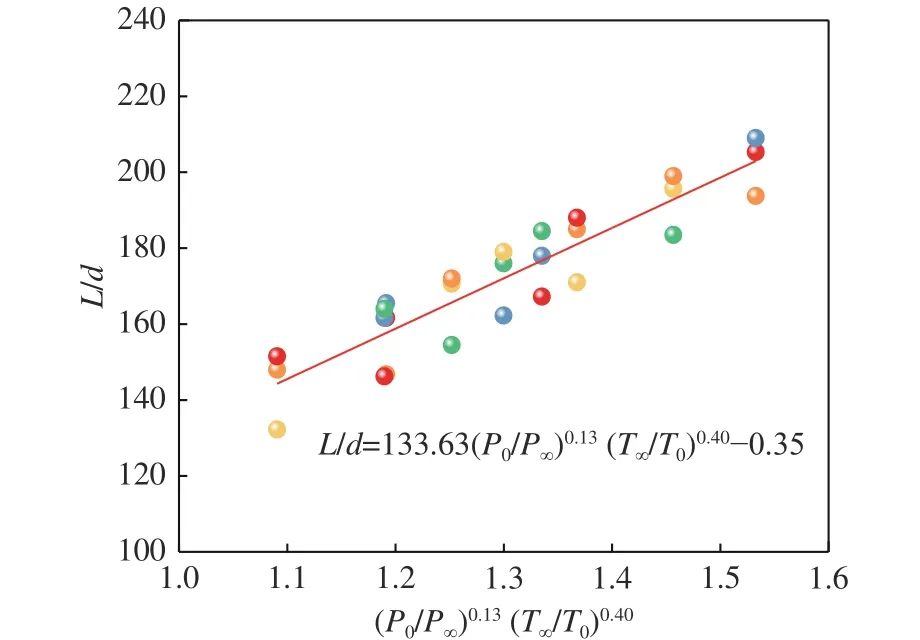
图19 CH4 泄漏危险范围长度经验公式Fig.19 Empirical formula of the length of CH4 leakage danger range

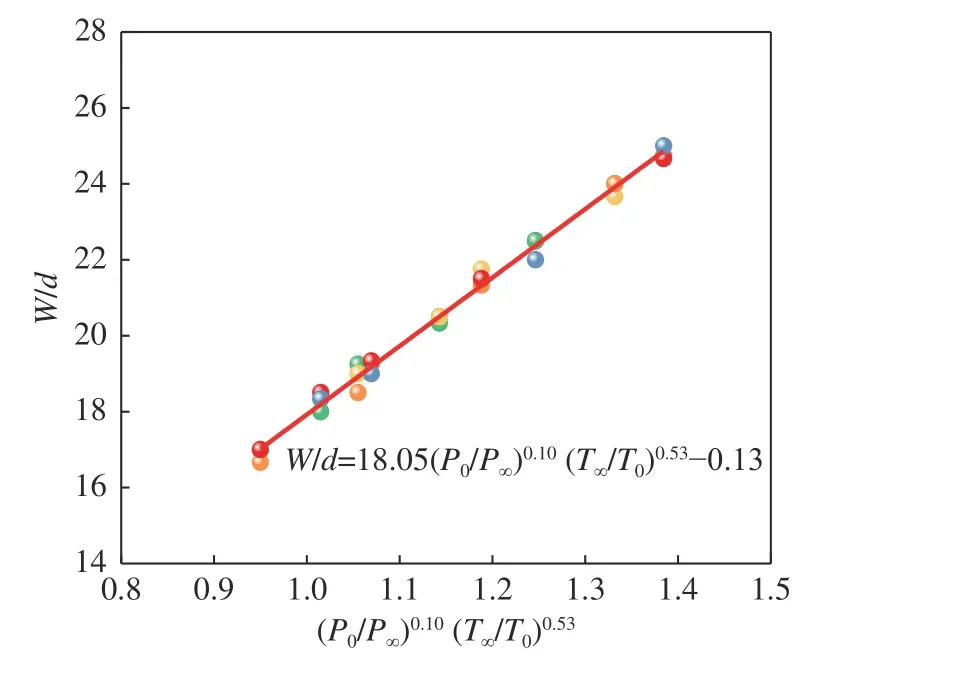
图20 CH4 泄漏危险范围宽度经验公式Fig.20 Empirical formula of the width of CH4 leakage danger range

对于H2：

对于CO：

对于CH4：

其中：L为泄漏危险范围长度，m；W为泄漏危险范围长度，m；d为泄漏口直径，m；P0为泄漏压力，Pa；P∞为环境压力（101 325 Pa）；T0为泄漏气体温度，K，T∞为环境温度，300 K。

3 结 论

1）3 种气体随着泄漏压力的增大，气体泄漏危险范围随之明显增加，且泄漏压力越大，泄漏口中心轴线气体浓度越高。

2）随着泄漏气体温度的增大，气体泄漏危险范围随之明显降低，危险范围除轴向长度及宽度均有所减小，泄漏气体温度越高，泄漏口中心轴线气体浓度越低。

3）随着泄漏口直径的增大，气体泄漏危险范围随之明显增加，危险范围轴向长度和宽度均有所增大，且泄漏口尺寸对于可燃气体泄漏危险范围的影响大于泄漏压力和泄漏温度。泄漏口直径越大，泄漏口中心轴线气体浓度越高。

根据数值模拟得到的危险范围数据，考虑气体、泄漏口大小、泄漏压力和泄漏温度后，对每种泄漏气体危险范围的长和宽分别进行拟合，得出泄漏危险范围预测经验公式。

4）通过可燃气体泄漏扩散规律和危险范围分析结果，可为区域救援协同响应和应急资源快速调配提供技术支持，亦可为重大工业（危险化学品）事故救援或城市公共安全事件处置应急指挥辅助决策提供参考依据。