考虑不同状态划分方法的马尔科夫链空调车备件需求预测

王炳忠 毛 宇 胡新生 胡海洋

（海军航空大学青岛校区 青岛 266041）

0 引言

在进行飞机地面维护和检查时，空调车为飞机设备舱提供冷、热、通风，以此调节机舱内空气温度和湿度，确保机载电子设备的正常运行。空调车备件数量直接影响着保障能力，备件不足会导致空调车战备完好率下降，而备件储备过多既增加管理难度，也浪费经费。因此，准确预测备件需求对于保证空调车保障能力、维持合理备件库存具备重要意义。

备件需求预测方法主要有三大类：基于人工智能、可靠性和历史数据[1-3]。基于人工智能的预测方法主观性和随机性较强，且需要大量统计样本；基于可靠性主要研究损坏机理，与备件的寿命分布有很大关系；基于历史数据即解析分析法，在预测备件需求时，运用较为广泛的是灰色马尔科夫组合模型。虽然灰色系统理论的GM(1,1)模型能够挖掘出少量样本数据中的发展趋势，但对于波动明显的数据预测精度较低，而马尔可夫链预测模型能够很好地弥补这一缺陷，实现优势互补。

文献[4-7]利用灰色马尔科夫模型及其改进模型对雷达备件的月度消耗量、油泵装机后发生故障的时间点、装甲车辆负载需求功率以及4S 店备件需求进行了研究，预测精度较高，由此可见灰色马尔科夫模型已较为成熟地应用在备件需求、装备故障预测等领域。在马尔科夫模型建立过程中，状态划分对于预测精度是极为重要的，因此本文重点研究马尔科夫链状态划分方式对于预测精度的影响。

1 模型建立[8]

1.1 GM(1,1)建模

（2）构造一阶常微分方程逼近累加生成序列，并用最小二乘法求得系统时间响应方程如下：

其中，a、u为待定参数。

（3）再累减还原，即可得到原始序列的时间响应方程（预测曲线方程）：

1.2 建立灰色－马尔科夫组合模型

（1）状态划分

（2）计算状态转移概率矩阵

状态转移概率为：

式中：Mi为系统处于状态i的原始数据样本数；M i j(m)为状态i经m步转移到状态j的原始数据样本数。

（3）计算预测值

若预测系统在某时刻处于i状态，则预测值为：

式中：iB和iA分别表示i状态的条形区域的上下限。

2 案例应用

已知某场站某型空调车连续15 个月的备件消耗数量，如表1 所示。

表1 某型空调车备件消耗数量Table 1 Consumption of spare parts of a certain type of air-conditioned car

（1）利用GM(1,1)来预测备件消耗量

令X(0)= ｛2 7, 33, 35, 21, 27, 23, 29, 31, 32, 27, 30, 30, 37, 29, 27｝，根据式（1）和（2），计算得到GM(1,1)模型的时间响应函数的参数a= - 0.0059 ,u= 27.8738，将每个月份的备件消耗实际值与灰色预测值反映在图1 中。图1 缺少了第1 个月的预测数据，因为在灰色模型建立过程中，第1 个数据作为初始条件求解未知参数，实际值与预测值相等。由这张图可以看出，每个月备件需求数量都有波动，但变化程度不大。预测曲线可以反映出备件需求量呈平缓上升的趋势，这与实际情况是符合的。为了反映灰色预测误差，我们将各月实际值与灰色预测值的比值列出，如表2 所示。

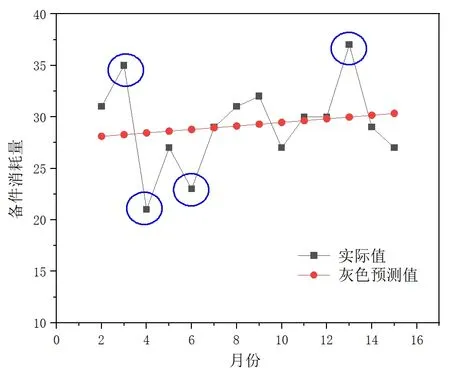
图1 各月备件消耗实际值与灰色预测值Fig.1 The actual value and gray forecast value of spare parts in each month

表2 各月实际值与灰色预测值的比值Table 2 The ratio of actual values to gray prediction values for each month

结合表2 中的数据，可以看出图1 中所示的第3，4，6，13 月份的灰色预测误差较大，其中第3，13 月份处于强上升状态，即预测值要比实际值大许多；而第4，6 月份处于强下降状态，灰色预测值比实际值小很多。因此在对各月份的灰色预测值进行修正时，需要对强上升以及强下降月份的状态作出准确预测，这样才能进行有效修正。而第7，11，12，14 月份的实际值与预测值比值为1.002，1.012，1.006，0.961，这4 个月份的预测误差均在5%以下，因此可以考虑不进行修正。

（2）状态划分

在构建马尔科夫模型时，划分状态的数量以及区间长度对于预测结果有很大影响，因此本文设置了四种划分方式，如表3 所示。其中四状态分别为：强下降、弱下降、弱上升、强上升，而五状态则是多出一种保持不变的状态。划分出来的区间有等值和等量之分，等值区间即各个区间长度相等，等量区间是通过保持各个状态数量均衡产生的，四种划分方式的具体参数设置如表4 所示。以划分方式三为例（下同），各月的状态如表 5 所示。

表3 划分参数Table 3 divide parameters

表4 四种划分方式具体参数Table 4 Specific parameters of the four division methods

表5 各月状态Table 5 The state of each month

（3）构造转移概率矩阵

根据式（3），得到各步转移概率矩阵为：

（4）编制预测表

因为是4 步转移概率矩阵，所以从第6 个月开始预测。通过第2，3，4，5 月份对第6 个月的备件消耗量进行预测，如表6 所示。

表6 第6 个月灰色马尔科夫状态预测Table 6 The 6th month of gray Marcow status forecast

由表6 中的合计栏可以看出，状态1’’对应的概率最大，所以第6 个月备件消耗量最有可能处于状态1’’，其灰色预测值为28.78，由式（5）可得，第6 个月马尔科夫修正值为21.87，而实际值为23，误差4.90%。接着我们对于剩余月份进行灰色马尔科夫状态预测，如表7 所示。

表7 第6-15 月份灰色马尔科夫状态预测Table 7 Gray Marcow status forecast for 6-15 months

（5）四种划分方式比较

以上我们以方式三为例，对灰色预测值进行了马尔科夫修正，接着我们采用其余三种划分方式进行预测，四种方式的实际值与预测值比较如图2 所示，四幅图中相关系数的大小表明预测曲线与实际曲线的贴合程度，贴合度从大到小依次为方式三（0.98），方式四（0.85），方式二（0.73），方式一（0.60）。其中，方式三的贴合程度最高，原因是该方式下的预测状态与实际状态完全一致，因此具有非常高的贴合率。而其他方式下的预测状态与实际状态偏差越大，预测曲线贴合程度越低。

图2 四种划分方式下实际值与预测值比较Fig.2 Comparison of actual values and prediction values in the four division methods

观察图2 上两幅图可以发现，方式一、二由于采用了四状态划分，缺少不变状态，其预测状态很大程度上偏离实际状态，概率矩阵失效，导致预测偏差较大。

而方式四在第13 个月误差很大，我们表示出其预测表，如表8 所示。可以看出第13 个月处于状态4’’’和5’’’的概率非常接近，状态4’’’的概率略大，而实际状态为状态5’’’，这是因为方式四追求各状态数量均衡，使得区间长短不一，区间长度分别为0.2，0.1，0.01，0.09，0.2。相比之下，方式三的等值划分，所得到的转移概率矩阵更加准确。

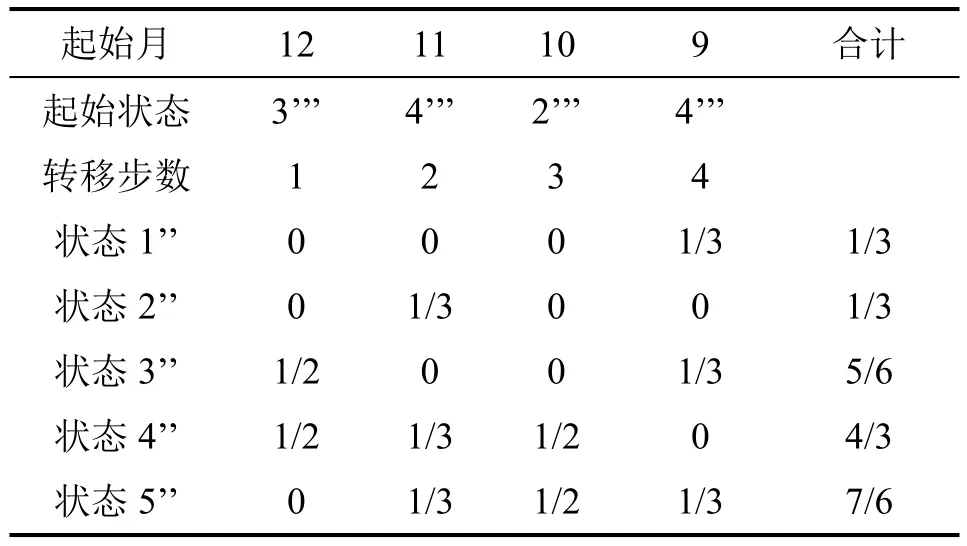
表8 方式四第13 个月灰色马尔科夫状态预测Table 8 The 13th month of gray Marcow's status prediction in the fourth way

3 结论

本文通过灰色马尔科夫组合模型对于空调车备件消耗量进行了预测，并比较了四种马尔科夫链状态划分方法对于预测精度的影响，结论是：

（1）在确定马尔科夫状态数量之前，应对灰色预测值进行误差分析，得出是否需要加入不变的状态；如果灰色预测结果中有部分数据与实际误差较小（5%以下），则有必要加入不变状态。

（2）在五状态划分时，采用等值区间的预测曲线具有更好的贴合度。如果一味追求各状态数量均衡，会导致各区间长度不一，最终使得概率矩阵状态预测不准确，得到的预测结果产生较大偏差。

（3）第四种划分方式下，第13 个月的预测状态处于4’’’和5’’’的概率非常接近，本文采用概率偏大的状态4’’’进行误差修正，如果采取加权计算，会使这一数据的误差有所减小。因此对于数值较小的数据预测，采用加权法可进一步减小预测误差，同时后期的研究方向是进一步完善马尔科夫链状态划分方法以及对于特殊数据的处理，在保证状态转移概率矩阵准确的基础上，才能确保预测精度。