含水层底部单孔非完整疏放水井渗流特征砂槽试验

王文学,郝清扬,薛景元,姜 彤,董金玉

(华北水利水电大学 河南省岩土力学与结构工程重点实验室,河南 郑州 450045)

深入地面以下开发利用地下空间及能源资源是21世纪人类工程活动的主要课题,我国是世界隧道和地下工程最多、发展最快、水文地质及结构形式最复杂的国家[1],复杂的水文地质条件对地下工程施工带来诸多困难。地下工程施工扰动围岩体形成不同程度的扰动裂隙,其贯穿联通是形成突水、涌砂、突泥等灾害的重要通道,对工程与生命财产安全构成严重威胁[2-3]。

疏水降压是解决水体下工程施工发生突水溃砂灾害的有效手段,包括地面抽排、井下疏放及地面与井下联合抽放等3种形式。对于深部地下工程,由地面施工钻孔(井)对目标含水层进行抽排水降压,钻进深度大、时间长、费用高。而疏放水目标含水层(体)通常距离地下作业空间较近,由地下空间向上施工仰斜孔对含水层(体)进行疏水降压更为经济、合理。仰斜钻孔疏放水因其施工难度低、疏放效率高,已作为一项成熟的地下工程水害防治技术[4-8]。

施工仰斜孔开展疏放水试验也是获取含水层水文地质参数的重要途径,但国内外目前并没有针对疏放水试验计算含水层水文地质参数的相关理论公式,多采用地面抽水试验相关理论公式计算含水层水文地质参数,其获取的渗透系数与抽水试验往往具有较大差别,含水层底部疏放水试验流量大是导致其获取的渗透系数比抽水试验大的主要原因[9]。刘基[10]通过采用稳定流和非稳定流计算含水层水文地质参数,指出采用非稳定流疏放水前2 h数据计算含水层水文地质参数较为合适;周振方等[11]基于系统动力学理论,提出了煤矿工作面推采采空区涌水双指数衰减动力学模型,并采用单指数模型对顶板含水层静储量低角度仰斜孔的疏放水特征进行拟合;赵宝峰[12]采用灰色关联度研究含水层厚度、钻孔孔深、方位角和仰角对钻孔疏放水效果的影响程度,指出钻孔孔深对疏放水量的影响最小,说明只要钻孔穿透有效含水层即可,过长的孔深不会有效的增加疏放水量;李明山等[13]从水力学中的伯努里方程出发,考虑水流的水头损失,推导出一种井下探放水钻孔涌水量计算的新方法;陈实等[14]以空间点源理论为基础,运用反映法,建立了均质各向异性无限水平承压含水层中非完整倾斜钻孔的井流计算方程,讨论了多个倾斜钻孔同时工作时,多孔叠加的疏放水井流计算方法;孙亚军等[15]应用有限厚度的承压非完整井理论,对某矿收缩开采阶段中封闭不良防尘取水孔的涌水量预测进行了讨论;孙启明等[16]结合现场疏放水试验数据采用Modflow-2005中的Conduit Flow Process方法对煤矿疏放水试验进行模拟,建立渗流-管流耦合模型,经过调参反演水文地质参数;虎维岳等[17-19]进一步明确的矿井涌水量定义及其所应具备的基本属性特征,指出浅埋煤层回采过程中顶板含水层充水水量由脉动式静储水量释放与渐增式动态补给水量共同组成,并给出了随矿井采掘过程进行的渐进式矿井涌水量时空动态预测方法;采动裂隙向上发育揭穿含水层的长度以及面积对工作面涌水量影响显著,以往多采用“大井法”对工作面的涌水量进行计算,将裂隙揭穿含水层区域看作同面积的大井,采用裘布衣完整井公式计算[19-21]。

仰斜疏放水孔(井)与地面抽放水井不同,地面抽水井需要井内汇集一定深度的水淹没抽水泵才能抽排出地面,大气压强直接作用在抽水井内水面。而仰斜疏放水孔(井)由含水层底部揭露含水层,此时虽是非完整疏放水孔(井),但含水层底板以上的水均可流向疏放水孔(井),且含水层上部空气不能直接透过含水层进入疏放水井。因此,研究含水层底部疏放水井渗流特征及其水压演变特征,对含水层底部疏水降压准确计算涌水量及水文地质参数尤为关键。笔者通过自主设计研发的一套扇形体疏放水砂槽模型开展了潜水含水层底部疏放水渗流试验,研究了含水层底部非完整疏放水井渗流特征,研究结果对合理开展疏水降压及准确利用疏放水试验计算含水层水文地质参数具有重要意义。

1 假定条件

图1 含水层底部疏放水孔(井)施工及分布示意Fig.1 Dewatering well seepage model for a single pipe from the aquifer bottom

2 疏放水砂槽试验系统及过程

2.1 疏放水砂槽模型试验系统

渗流疏放水砂槽为扇形箱体,角度为60°,砂槽垂向深度为70 cm,径向长度为210 cm,圆弧外边界有10 cm宽稳压槽,砂槽三角圆心位置底部安装疏放水井片花管。疏放水砂槽模型试验系统还包括1个供水箱、2个集水箱、3个流量计、2个循环水泵、8个水压传感器、水位监测系统及流量数据自动采集系统;渗流砂槽底部设置有2个底部进水口用于饱和砂体,供水口集水箱放置于高处可自动向稳压槽及底部进水口供水,放水口集水箱及溢出口集水箱收集的水由循环水泵抽取至供水口集水箱,整个渗流装置实现了水的循环利用,疏放水砂槽模型试验系统如图2所示。砂槽箱体侧面布设有水头监测管,该部分水头变化采用数码相机监测,同时在放水口井片上方布设8个水压传感器用于实时自动监测井片上方不同位置压力水头变化,本文疏放水过程水压变化特征主要基于8个水压传感器监测数据展开分析。

2.2 试验过程

试验时首先将疏放水井及井盖安装在砂槽箱体圆心角位置,然后每10 cm逐层铺设河砂并适当密实。砂体铺设完毕后,反复饱和排放水5至6次,充分固结,使其渗透系数保持稳定;然后打开电磁流量计、数据采集系统、疏放水井底部渗流开关,同时打开数码相机监测水头变化;疏放水试验过程中稳压槽水位稳定在58 cm,其供水量、溢出量分别由电磁流量计A、B监测,疏放水井口流量由流量计C监测;每组井片试验结束后更换井片,并重复饱和固结过程。

渗流砂槽内砂体厚60 cm,砂槽圆弧外边界水头维持在58 cm。采用经过筛分的普通清水冲洗过的河砂,其级配曲线如图3所示,大于0.5 mm粒径质量分数为68.33%,小于0.25 mm粒径质量分数为3.44%,为粗砂,根据测试该砂体稳定渗透系数为0.138 cm/s。

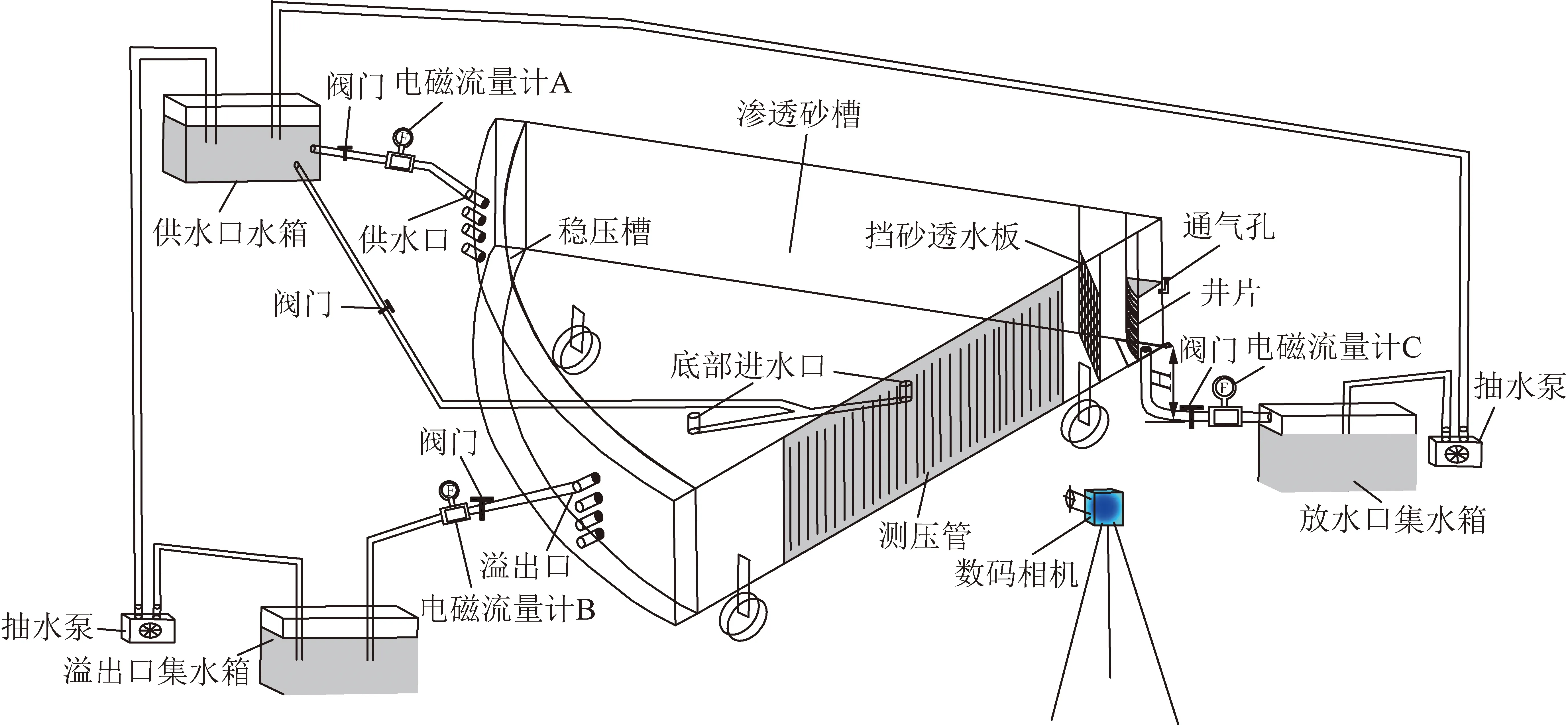
图2 砂槽模型试验系统示意Fig.2 Sand tank test system schematic diagram

图3 渗透砂体级配曲线Fig.3 Grading curve of permeable sands

通过控制疏放水口阀门可在放水管进水口位置形成不同压力水头p1,该压力可由1号水压传感器实时监测,在井片内部及其垂直上方布设8个水压传感器,其中1号水压传感器位于疏放水管进水口位置,各传感器位置、间距如图4所示。疏放水前各水压传感器压力水头自动监测数据及其各传感器之间压力水头差分布如图5所示,各传感器压力水头随其埋深增加而增大。笔者以疏放水井半径为80 mm,井长为40、80、120、150 mm井片,井片底部透水的疏放水试验结果开展分析,每种井长可开展7～8组不同压力水头p1的放水试验,不同井长试验中形成不同的压力水头p1见表1,共计31组。试验时不同井长疏放水管进水口很难获得对应的相同压力水头p1,井长较大时井内负压很难形成。试验时首先保持通气孔处于闭合状态,逐级调整疏放水口阀门获取不同压力水头p1,为了避免空气进入井片,逐级放水过程中不包括放水管进水口压力为0,放水管进水口压力为0需要打开通气孔,重新饱和砂体、单独开展。注:井片内部压力上下大小不一致,P为一个综合值,下文为便于分析以放水管进水口压力水头p1来反映井内压力,开展分析。

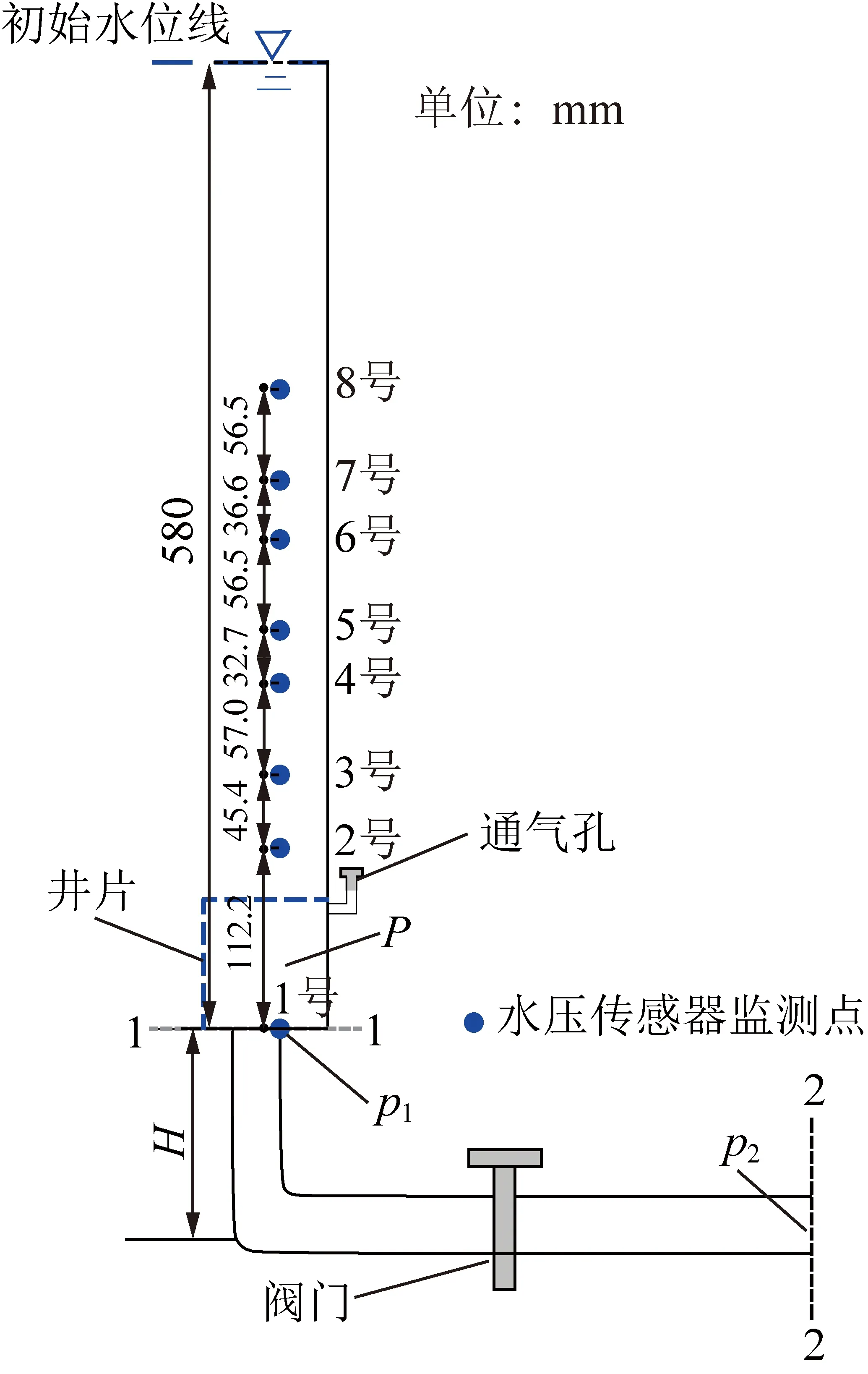
图4 疏放水口上方水压传感器分布Fig.4 Distribution of water pressure sensors above the outlet

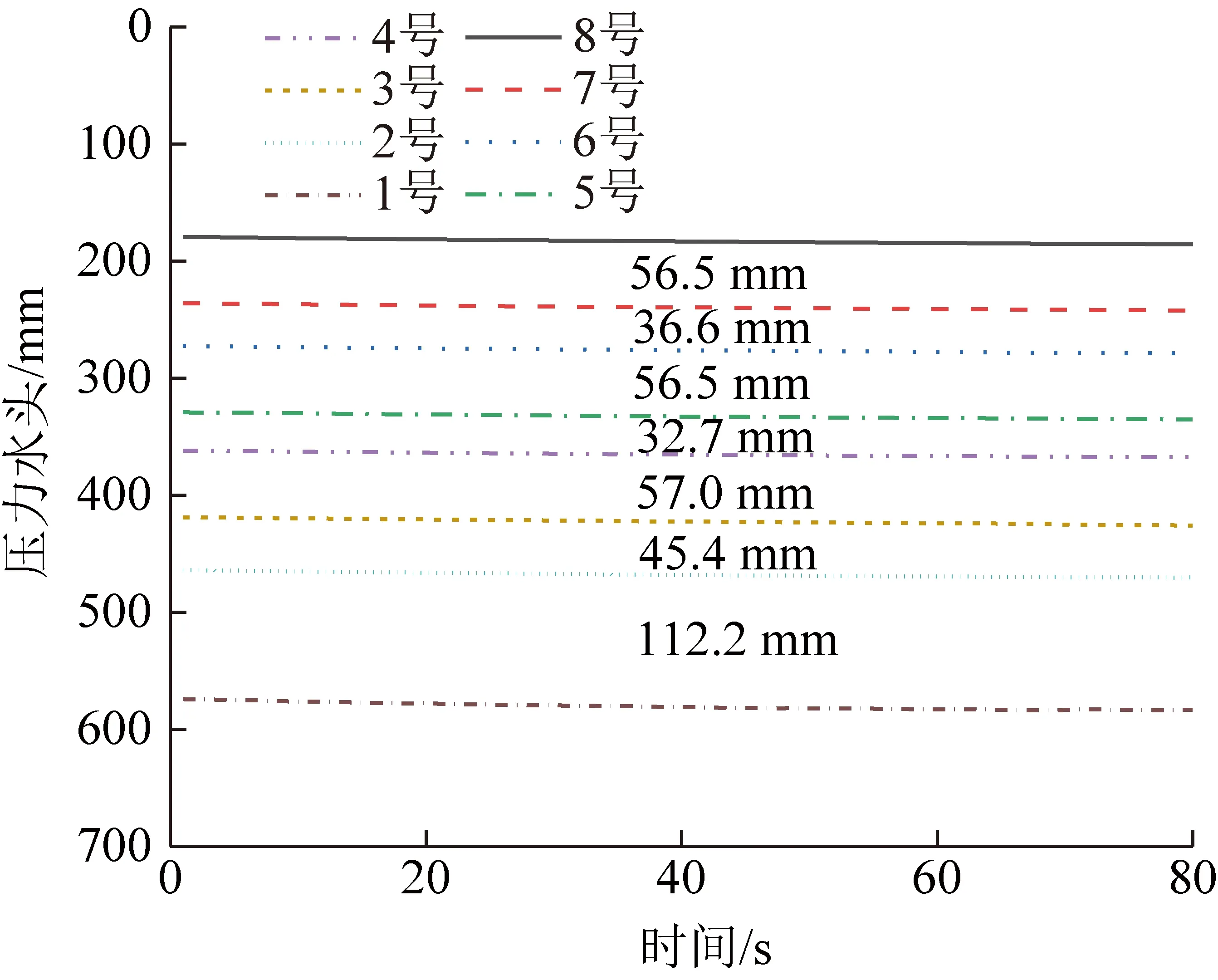
图5 水压传感器初始压力水头Fig.5 Initial pressure heads of water pressure sensors

表1 试验中不同井长lw不同压力水头p1Table 1 Different water pressure heads for p1of different well length in sand tank test

3 砂槽试验结果及分析

3.1 完整井流量砂槽试验

为验证渗流砂槽试验结果的可靠性,开展含水层底部非完整井疏放水试验之前,对同井径完整井开展了不同降深渗流试验,半径为80 mm的完整井不同降深条件下的疏放水渗流量及采用Dupuit式(1)对各降深条件下的渗流进行理论计算结果如图6及表2所示。

(1)

式中,K为渗透系数,取值0.138 cm/s;M2为潜水含水层厚度,取值58 cm;R为影响半径,取值为砂槽模型箱半径210 cm;rw为井的半径,取值8 cm。

图6 完整疏放水井Dupuit公式计算与砂槽试验渗流量Fig.6 Relationship of seepage flow between sand tank test and Dupuit formula for complete dewatering well

由图6和表2可以看出,完整疏放水井在不同降深条件下砂槽试验疏放水渗流量与采用Dupuit式(1)所计算的结果较为吻合,不同降深条件下2者误差在18%以内,且降深越大吻合度越高,说明该渗流砂槽的完整井渗流量可以采用Dupuit公式计算,

表2 完整疏放水井砂槽试验与Dupuit公式计算流量比值Table 2 Seepage flow ratio of Dupuit formula to sand tank test

且该砂槽渗流系统可以较好地开展含水层底部疏放水试验。

3.2 非完整疏放井渗流特征

3.2.1 压力水头变化规律

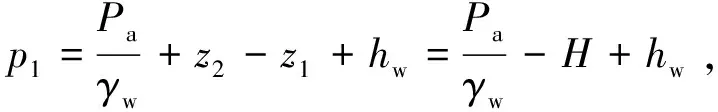
(2)

式中,z1为截面1处的位置水头;p1为截面1处的压力水头;u1为截面1处的水流速度;z2为截面2处的位置水头;p2为截面2处的压力水头;u2为截面2处的水流速度;hw为沿程损失水头。

渗流过程动、静态储量变化将影响砂槽内压力水头的分布,不同井长在疏放水管进水口不同的压力水头下,在动、静态补给量动态转换平衡中,井片的渗流量及在其上方压力水头的分布也发生改变。浸润线将随着井内压力水头的降低而逐渐下降,浸润线降低至传感器位置并继续下降时,在该传感器位置将形成负压,且负压绝对值随浸润线的降低逐渐增加,当浸润线下降至距离上部传感器位置较远时,该传感器压力水头由负压最大绝对值突变为0,即大气压强,说明上部空气进入该传感器位置,井片高度为40 mm疏放水过程中各压力传感器压力水头变化如图7所示。由图7可以看出,水压传感器8号、7号、6号随埋深位置的增加依次形成负压,该负压的形成为饱和毛细水所致,随着浸润线的下降处于饱和毛细带的传感器负压绝对值进一步增加,当其仍位于饱和毛细带时,减小p1该传感器会很快响应且负压力绝对值激增,当饱和毛细带下降至该传感器位置之下时空气进入压力突变为0;当减小p1时,监测点传感器仍位于饱和毛细带内,其压力水头一直持续为负值,且随p1的减小而减小,如5号、4号、3号、2号水压传感器变化规律所示。

根据非完整井疏放水过程中,各水压传感器监测数据变化规律可以将含水层底部非完整疏放水井上部可划分为上层毛细水带、支持毛细水带、饱和毛细水带及自由水饱和带,如图8所示,图中绿色间断线为饱和毛细水带与支持毛细水分界线、蓝色间断线为自由水饱和带与饱和毛细水带分界线。当然,如果含水层厚度较小、疏放水井长度较大时,非完整疏放水井上部含水层内饱和毛细水带及自由水饱和带将消失,空气可由含水层上部进入非完整疏放水井。

将疏放水管进水口位置p1降低,该压力在经过略微调整后将趋于稳定,如图7所示。不同井长不同阶段疏放水过程中,p1达到似稳定状态时,其井片垂直方向各压力传感器的稳定压力分布如图9所示,图9图例为p1稳定值大小,各曲线表示在p1稳定值条件下不同垂直位置压力水头的大小。

图8 含水层底部非完整疏放水井上部含水层水的垂直分带特征Fig.8 Water vertical zoning distribution characteristics above partially penetrating dewatering well in an aquifer

图9 井片垂直方向压力水头分布特征Fig.9 Water pressure heads vertical distribution characteristics

由图9可以看出,当p1大于井片高度时,井内为满管,井片由下而上自由水连续分布,井片垂直方向由下而上压力水头逐渐减小,图9中各井长高度均满足此规律,可概化为如图10(a)所示的水位线分布模型。当p1小于井片高度时,井片内部为非满管,井片上部将形成负压,下部存在一定压力水头,由于渗透砂体与渗流水内仍含有一定的空气,当p1略小于井片高度时,井片上方随即也形成一定非满管段,但该段内负压并不明显,井片上方存在一定范围自由饱水带及饱和毛细水带,如图9(d)井片高度150 mm,p1为123 mm,其上部水位线分布可概化为10(b)的模型。当p1较大幅度小于井片高度时,如图9(c)井片高度为120 mm,p1为52 mm,图9(d)井片高度为150 mm,p1为40 mm与77 mm时,均在井片上部形成明显的负压区,井片上方没有形成自由水饱和带、只有饱和毛细水带,其水位线分布模型可概化为图10(c)。当p1小于0时,由本次模型试验结果可知,井片上方均不存在自由水饱和带,但均存在饱和毛细水带,井片上方水位分布可概化为图10(e),本次试验模型渗透砂体厚度为60 cm,如果砂体厚度增加,即便井内压力小于0,井片上方也应该存在自由水饱和带,如图10(d)所示。当p1为0时,井片高度较小,如图9(a)、(b)所示,在其上方形成自由饱水带及饱和毛细水带,井片上方水位分布可概化为图10(f);当井片高度较大时,如图9(c)、(d)所示,在井片上方既不存在自由水饱和带也不存在饱和毛细水带,水位分布模型如图10(g)所示。经上述分析,含水层底部非完整井井片内部存在4种水压分布形态,即P=0、P>0、P<0以及Pup<0且Pdown>0,根据井内内压力及井片上部自由水饱和带、饱和毛细带的分布情况,含水层底部非完整井疏放水似稳定流态井内压力及上部水位分布模型可以概化为如图10所示的7种模型。

图10 非完整疏放水井井内压力及上部水位分布模型Fig.10 Inner water pressure and upper water level distribution models for partially penetrating dewatering well

当井片内压力水头为负值时,井内负压与饱和毛细水负压之间平衡转换后导致井片上部各压力传感器有效监测值均为负值,说明井片上部浸润线已向模型动态补给侧退化,饱和毛细水带主要由侧向浸润线补给维持。井片内非满管段的形成导致其上部自由水压力不能连续传递,井片自下而上压力水头分布不再遵循单纯的递减关系,如果其井片上方存在浸润线,压力水头分布由下而上呈先增加后减小的规律,如图9(a)、(b)所示中井片高度40、80 mm且p1为0的情况;当井片上方存在饱和毛细水带时可以有效隔绝上部空气与井内压力的联系,一旦饱和毛细水带消失井内压力将为0。

3.2.2 疏放水井片流量变化规律

由上述分析可知,非完整疏放水井内压力水头上下存在差异性,可形成上部负压、下部正压的复杂情况,其井内压力水头很难用某一准确值表示。笔者以疏放水管进水口位置p1与渗流量关系开展分析,疏放水管进水口不同压力水头p1达到似稳定状态时的渗流量变化如图11所示,图中红色间断线为对应井长的压力水头,井片疏放水量随p1减小呈增加规律,当p1较大时(大于井长)或p1小幅度小于井长时,井片渗流量随p1减小呈线性增加;当p1较大幅度小于井长时,井片内部负压区的形成将增加井片外围渗透砂体的渗流量,较大幅度的影响井片渗流量,井片渗流量不再与其呈线性关系。

当井片上方存在自由水饱和带或较大范围的饱和毛细水带时,井内压力的减小将有效增加井内渗流量,当自由水饱和带消失且饱和毛细水带垂直分布较小时,井内压力的减小对渗流的增加效应不明显。井内负压影响为主时,井片渗流量将大于井内压力为0时的渗流量。

图11 不同井长不同p1下渗流量变化Fig.11 Seepage flow variation with different inner water pressure heads p1 for different well length

当井内压力为0时,不同井长似稳定状态时渗流量如图12所示,由图12可以看出,当井长较小时,流量随着井长的增加而增加,当井长大于某一临界值后,流量不再随着井长的增加而增加。以往生产实践中认为含水层底部疏放水井一旦揭穿含水层,其上方孔隙水压力会骤降为0,文献[12]也指出钻孔孔深对疏放水量的影响最小,只要钻孔穿透有效含水层即可,过长的孔深不会有效的增加疏放水量的结论不同。砂槽试验证明:当疏放水井上方孔隙水压力大于0,井长小于临界井长时,增加疏放水井进入含水层的长度可以显著增加疏放水量,在有条件的情况下,疏放水井钻进含水层至临界井长将达到最优疏放水效果,超过临界井长后的钻进尺寸对疏放水量的增加没有效果。现场施工过程既不能一味追求疏放水井的长度,也不能过小的设计疏放水井的尺寸。

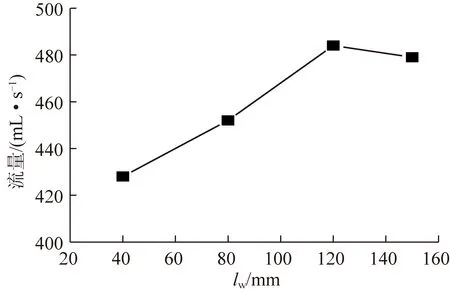
图12 p1=0时井片渗流量随井长变化关系Fig.12 Seepage flow variation with well length with p1=0

3.3 动静储量变化特征

疏放水井的放水量由含水层静储量及动储量构成,为研究动静储量在疏放水过程中的变化特征,砂槽渗流模型中设置电磁流量计A、B、C分别监测稳压槽供水流量QA、稳压槽溢出口流量QB以及疏放水管流量QC。动态补给量Qd=QA-QB,静态补给量Qj=QC-Qd=QC-QA+QB。不同井长疏放水井第1级疏放水压力水头(表3)疏放水流量及动静补给量变化特征如图13所示。

由图13可以看出,各井长第1级疏放水压力水头下疏放水口流量快速趋于稳定,刚开始放水时疏放水口以静态补给为主动态补给量很少,随后静态补给量快速减少、动态补给量快速增加。通过公式拟合发现,静态补给以一阶指数函数减少、动态补给以一阶指数函数增加,分别可以由式(3)、(4)描述,其相应的拟合公式见表3,其拟合公式相关系数R2均大于0.95。

Qj=Qj0+(Qj0-Qje)e-αt

(3)

Qd=Qd0-(Qde-Qd0)e-αt

(4)

式中,Qj为疏放水时间为t时静态补给量;Qj0为初始阶段静态补给量;Qje为似平衡状态时静态补给量;α为拟合参数;t为疏放水时间;Qd为疏放水时间为t时动态补给量;Qd0为初始阶段动态补给量;Qde为似稳定状态时动态补给量。

结合表3拟合参数及式(3)、(4)中各参数在试验中所获得的结果进行误差分析见表4,拟合公式所获得的参数与试验结果误差均小于5%,式(3)、(4)可以有效的反应疏放水过程中动静补给量的变化特征。

表3 动静补给量拟合公式Table 3 Fitting formula of dynamic replenishment and static reserve release

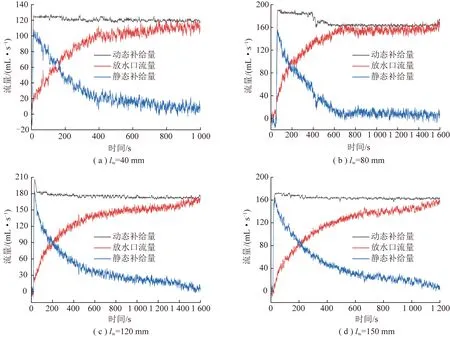
图13 动静补给量变化特征Fig.13 Variation characteristics of dynamic replenishment and static reserve release

表4 误差分析Table 4 Parameter error analysis

4 结 论

(1)含水层底部非完整井疏放水其上部可划分为上层毛细水带、支持毛细水带、饱和毛细水带及自由水饱和带,饱和毛细水带可有效阻止上部空气进入井内,井长的增加或井内压力的减小均可导致自由水饱和带与饱和毛细水带衰减、消失;井片内非满管段的形成导致其上部自由水压力不能连续传递,井片自下而上压力水头分布不再遵循递减关系,如果其井片上方存在浸润线,压力水头分布呈先增加后减小的规律。

(2)含水层底部非完整井井片内部压力存在P=0、P>0、P<0以及Pup<0且Pdown>0等4种水压分布形态,根据井内压力及井片上部自由水饱和带、饱和毛细带的分布情况,含水层底部非完整井疏放水似稳定流态水压分布可概化7种模型。

(3)当井片上方存在自由水饱和带或较大范围的饱和毛细水带时,渗流量随井内压力减小呈增加趋势,当自由水饱和带消失且饱和毛细水带垂直分布较小时,井内压力的减小对渗流的增加效应不明显。

(4)非完整井井长对含水层底部疏放水渗流量具有较明显影响,渗流量随井长的增加呈递增关系,但当井长大于临界值后,渗流量不再随着井长的增加而变化。

(5)疏放水过程中,初始阶段渗流量以静态补给为主,随后静态补给量快速减少、动态补给量快速增加,通过公式拟合发现,静态补给以一阶指数函数Qj=Qj0+(Qj0-Qje)e-αt减少、动态补给以一阶指数函数Qd=Qd0-(Qde-Qd0)e-αt增加。