高速运动声呐海底宽带混响建模与仿真

杨佳宜,杨云川,李永胜,石 磊,杨向锋

(中国船舶集团有限公司 第705 研究所,陕西 西安,710077)

0 引言

混响是影响声自导鱼雷工作性能的主要因素,鱼雷在声速近似满足负梯度分布的浅海水域进行目标探测时,海底混响是主要的干扰源。因此,为提高声自导鱼雷的主动探测性能,需要对海底混响规律进行深入的研究。

海洋中存在着大量的散射体,这些散射体的种类繁多且无规则,如各种类型的海洋生物、气泡、砂砾和由海水中温度不均造成的冷热水团等。声呐的发射信号在传播过程中遇到这些散射体时会产生声散射,同时,不平整的海面及海底介质也会使声信号发生散射。这些散射信号在接收端叠加就构成了混响[1]。由于混响的产生机理,其在频域上的覆盖区域与发射信号基本重合,在时域上与发射信号及目标回波强相关[2]。为区分接收信号中的混响与目标回波,需要进一步分析混响信号的统计特性。但是,考虑到获得实测混响信号所需的财力和人力等成本较高,且在某些自然条件下的测量数据难以复现。为解决这一难题,可将海洋环境信息与声呐系统信息数字化,通过仿真软件模拟混响信号[3]。

长期以来,国内外学者针对海洋混响做了大量研究工作,但现有模型仍存在一些缺陷[4-7]。例如,采用基于半经验性质的Lambert 散射模型由于计算过程没有环境参数,得到的混响信号缺乏相应的物理意义[8];REVMOD 模型仅在声速剖面保持不变且海面和海底不存在声反射的情况下适用[9];对功率谱采用批处理方式转换获得混响信号仿真序列的方法,存在实时连续性较差的缺陷[10]。

文中针对声呐平台配置、实际海洋环境和传播声线对混响的显著影响,建立了一种基于Bellhop模型的海底混响数值模型。该模型既全面考虑了散射体的散射、多普勒频移、发射波束指向性以及传播衰减对海底混响的共同作用,又具有实时性,且满足参数可调的要求。最后,通过分析仿真信号的统计特性,并将其与实测信号作相似性对照,验证了模型的准确性。

1 海底混响建模

由于混响的产生受到海洋环境、发射波束等多种因素的影响,当对其进行建模时,需要忽略次要因素以突出主要因素,从而平衡仿真的精确性和可行性[11],因此,作如下假设:

1)海底散射体的密度足够大,即在每一面积元上都有大量散射体;

2)各散射体对混响的贡献大致相同;

3)忽略面积元尺度范围内的传播效应;

4)忽略二次以上的散射。

1.1 海底混响信号仿真思路

构建混响信号的网络模型,将混响的产生理解为发射信号与混响散射特征函数的卷积[12]。其中,发射信号是原发射信号结合时延和平台运动带来的多普勒频移的运动发射信号。根据每个散射单元与平台的相对位置和海洋环境参数来确定其影响因子,包括海底散射强度、声压散射系数对到达信号的散射作用、波束指向性,以及信号在海洋信道双程传播过程中产生的扩展损失及吸收损失,从而得到的混响散射特征函数,最终将运动发射信号与混响散射特征函数作卷积,即可得到混响信号。

根据上述思路,可以得到海底混响信号网络模型的框架图,如图1 所示。

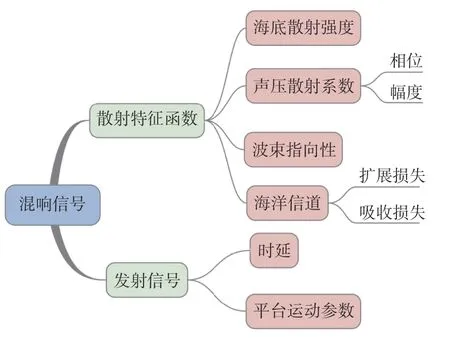
图1 海底混响网络模型框架图Fig.1 Frame diagram of the subsea reverberation network model

1.2 海底混响信号几何模型

海底存在着大量散射体,为了体现平台的运动、指向性和传播损失等因素对混响信号的影响,以及降低计算复杂度,文中采用非均匀划分的单元散射模型来计算混响[13]。

由于发射波束的束宽限制,实际的有效散射区域是所对圆心角为波束束宽的扇环,将该扇环按一定步长等半径距离、等方位角地划分为Nr×L个散射单元,每个散射单元的面积仍按照小扇环计算,其包含的散射体数量服从泊松分布。

鱼雷沿速度方向(设为Y轴正方向)作航速大小为v的匀速直线运动,其收发合置声呐的平面阵阵元按间距d均匀布阵,阵列轴向向量设为X轴,发射声波的波长为λ,海底任一混响散射单元相对于X轴的入射角为θ,相对于Y轴的方位角为α,鱼雷相对于XOY坐标平面的夹角为俯仰角β,混响模型的几何结构图如图2 所示。

图2 海底混响模型几何结构图Fig.2 Geometric diagram of the subsea reverberation model

对声呐阵元加遮挡时,不考虑后向辐射,所以有效散射区域仅分布在阵列的前方。

1.3 海底混响信号数学模型

对于收发合置的声呐,综合考虑阵列指向性、海底散射强度、声波传播中的扩展损失、吸收损失以及海底不同介质的影响[14],可得阵列接收到的混响信号为

式中:Nr为距离分辨单元数量;L为方位角分辨单元数量;B代表阵列的发射波束指向性;A为声压散射系数的幅值,服从正态分布;ϕ为声压散射系数的随机相位,服从0～2π 的均匀分布;Sr代表海底散射强度,且;f(r)为界面散射和信道传输的损失函数,通过Bellhop 模型计算得到;Np为每个散射单元内的散射体数量,且服从泊松分布;x(t)为阵列发射信号;τn为双程传播时延。

距离单元被允许的最大时延间隔τ小于混响的时间相关半径,对于连续波(continuous wave,CW)等窄带信号,其混响的时间相关半径约等于信号脉宽ts,所以τ≤ts;对于线性调频(linear frequency modulation,LFM)等宽带信号,混响的时间相关半径与信号带宽成反比,所以τ≤1/B。因此,文中τ=1 ms,在距离方向上,按cτ/2 划分Nr个散射单元;在方位角方向上,按ω(ω=1°)为步长划分L个散射单元,故在鱼雷波束海底作用的范围内,一共有Nr×L个散射单元。

文中为了平衡仿真精度和计算速度,同时考虑海底底质参数的影响,Sb直接使用GABIM 模型计算。

1.4 信道传播中的传播损失计算

海洋及其上下界面共同形成一个非常复杂的声传播介质,声信号在水中传播时会产生失真、减弱等声学现象,传播损失作为一种声信号可定义为由扩展损失和吸收带来的损失之和。

通常认为浅海的扩展介于球面扩展和柱面扩展之间,再加上吸收损失,可得粗略近似的传播损失,其经验公式为

式中,α为吸收系数,且

但上述方法并未考虑声信号在海洋中具体的传播路径,为弥补这一不足,文中使用射线Bellhop模型,通过高斯波束跟踪方法计算在二维平面内声线传播轨迹[15],进而对水下声传播损失进行定量仿真。

在某海试测得的水文条件下,信号频率为30 kHz,海深为73 m,海底密度为1.43 g/cm3,海底声速为1 535 m/s,声速与深度呈负相关,鱼雷所处深度为58 m,声线数为101,垂直发射角为[-10°,10°],通过以上两种方式仿真得到海底距接收点水平距离为0～1 000 m 的传播损失,仿真结果如图3 所示。

图3 不同方法得到的传播损失Fig.3 Transmission loss obtained by different methods

从图3 可以看到,基于Bellhop 模型得到的传播损失呈振荡增加的趋势,其包络幅值与基于经验公式的结果大致相同。其中,基于Bellhop 模型得到的传播损失,在0～80 m 的范围内大于100 dB,均按100 dB 计算;在600～850 m 的范围内急剧增大,这是因为此段由于折射的原因没有声线抵达(即声影区),在870～1 000 m 的范围内直达波与反射波同时抵达(即会聚区),因而传播损失出现异常振荡。Bellhop 模型较好地处理了能量焦散和绝对影区等问题,因此,考虑声线传播的Bellhop 模型计算得到的传播损失与实际声线图更加相符。

2 混响仿真及特性分析

仿真参数如下:海深为73 m,鱼雷所处深度为58 m,鱼雷的水平运动速度为25 m/s,阵列为6×6的平面阵,半波长间距均匀布阵。发射信号共有2 种:1)脉宽为150 ms、基频为20 kHz 的CW 信号;2)脉宽为100 ms、带宽为1 kHz、基频为28 kHz的LFM 信号。混响仿真流程图如图4 所示。按照以上流程,其中传播损失前0.11 s 的值可通过拟合计算得到,得到的仿真信号时域波形如图5所示。

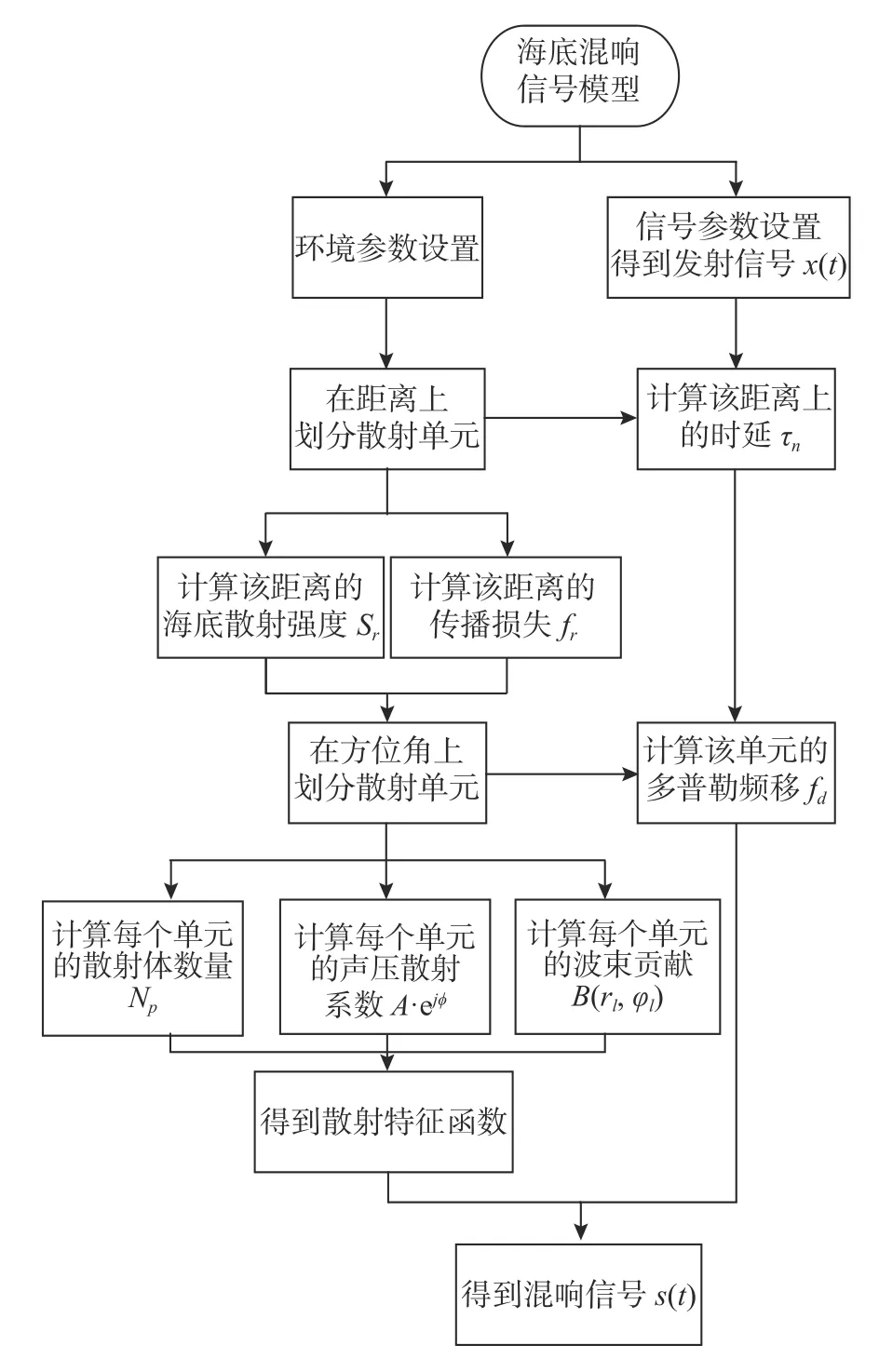
图4 混响仿真流程图Fig.4 Flow chart of reverberation simulation

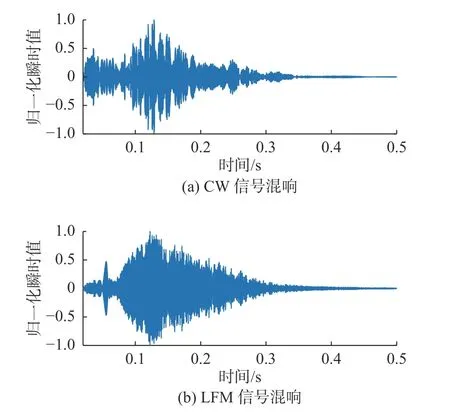
图5 仿真信号时域波形Fig.5 Time domain waveform of the simulated signal

从图5 中可以看出,CW 信号与LFM 信号混响幅度的整体趋势均为先增大再减小,最终趋于0。以LFM 信号为例,在0.02～0.13 s 阶段,信号幅值整体呈增大趋势,此阶段俯仰角β从-77.3°变化至-8.8°,接收点距离的变化范围为3.3～96.7 m,由图3 可知,传播损失的变化范围约8 dB,而由6×6 平面阵的波束方向图(图6)可以看出,此过程中波束指向性B随着俯仰角趋近于0°而大幅度增大,变化范围约25 dB,所以近距离处的混响信号幅值主要受波束指向性影响,且两者呈正相关;之后,混响的强度主要受距离影响,随着传播距离的增加,传播损失增大,海底散射强度减小,且两者对信号幅值的影响远大于阵列指向性的作用,因此混响信号的幅值随之减小。

图6 6×6 平面阵的3D 波束方向图Fig.6 3D beam pattern of 6×6 planar array

混响信号是典型的时变信号,对仿真信号进行时频分析,结果如图7 和8 所示。

图7 CW 仿真信号时频分布图Fig.7 Time-frequency distribution diagram of CW simulation signal

从图7 和图8 中可以看出:CW 混响信号与LFM 混响信号的中心频率随时间发生变化,这体现了混响信号的时变特性,但两者在中心频率附近均有一定程度的频移,且负频移更为显著,这是由频谱泄漏导致的。同时,频带有许多明显的毛刺,这是由于声场起伏带来的频率瞬态起伏。

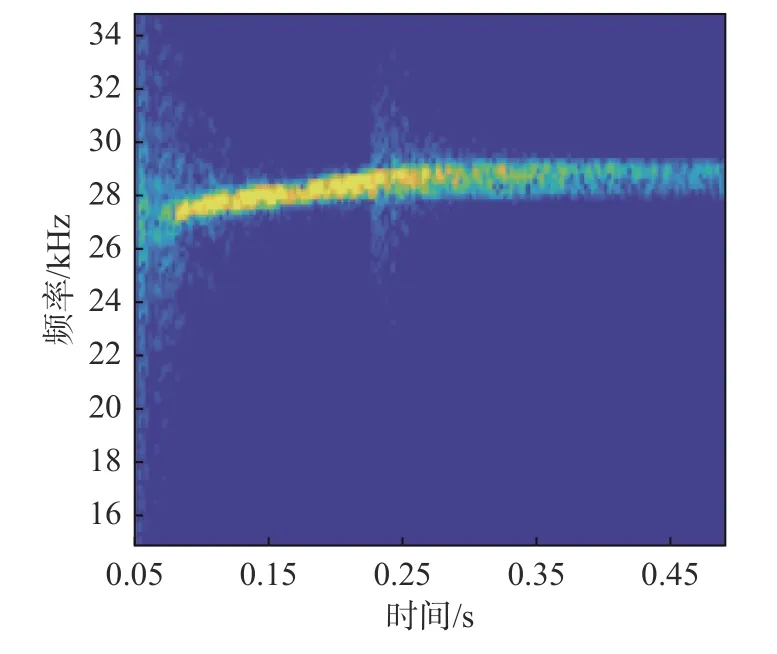
图8 LFM 仿真信号时频分布图Fig.8 Time-frequency distribution diagram of LFM simulation signal

图9 和图10 给出了传统方法(只考虑散射及多普勒效应影响的方法)和改进后方法的仿真信号瞬时值的概率密度函数(probability density function,PDF)与某实测信号值的相似性对照。可以看出,改进后的CW 信号与LFM 信号与对应的实测信号服从同一种分布,以PDF 的点积比为评价标准定量描述2 个信号的相似性,计算结果如表1 所示。

图9 CW 仿真信号与实测信号瞬时值的概率密度Fig.9 Probability density of instantaneous values of CW simulated and measured signals

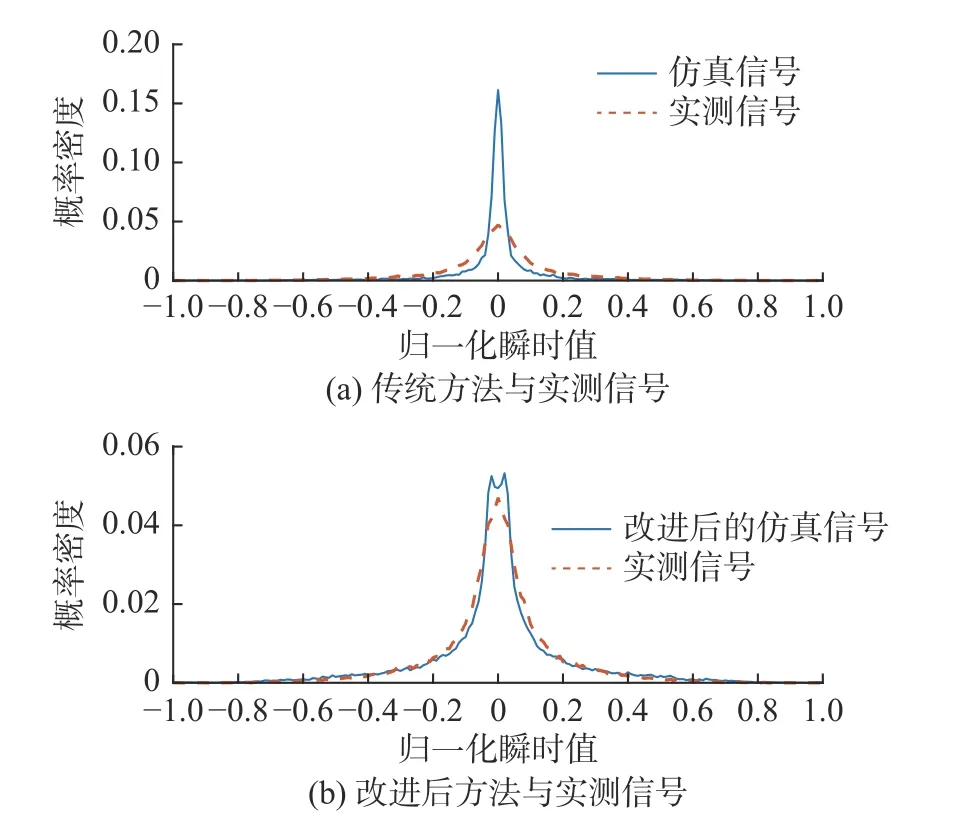
图10 LFM 仿真信号与实测信号瞬时值的概率密度Fig.10 Probability density of instantaneous values of LFM simulated and measured signals

表1 不同方法仿真信号与实测信号PDF 点积比Table 1 Dot product ratio of simulation signals and measured signals for different methods

由表1 可得,改进后的CW 混响信号、LFM 混响信号与实测信号的PDF 点积比较之前的增幅均在0.6 以上,表明了相似性较传统仿真信号有大幅度提高,证明了改进模型的有效性。其中,实测信号的瞬时值概率密度比仿真信号略有展宽,这与声压散射系数的相位范围有关。由于海底粗糙度不同,不能简单地定义海底声压散射系数的相位范围为(0～2 π),需要根据实际起伏情况来确定其相位的范围,文中对此不展开讨论。

3 结束语

文中在兼顾混响仿真模型的准确性和可实现性的情况下,改进了传播损失的计算方式,提出了一种综合考虑波束指向性、海洋环境等多种影响因素的基于Bellhop 模型的运动声呐海底混响模型,分析了仿真信号的时频域特性,并以信号瞬时值概率密度分布这一统计特性为评价标准,证明了该模型可以提高仿真信号与实测信号的相似程度。同时,该模型满足参数可调的需求,可以根据条件的变化,实时得到较为精确的混响数据,可为抑制混响的算法研究提供数据参考。后续将通过考虑不同海底底质的参数来进一步提高模型精确度。