碳纤维热导率与其微观结构参数的关系

何端鹏 张磊 高鸿 李岩 王茹

（1 中国空间技术研究院，北京 100094）

（2 战略支援部队航天系统部装备部军代局北京一室，北京 100074）

文摘 碳纤维具有多晶多相特性，为了研究微晶结构特性对热导率的影响，本文通过XRD 对碳纤维的微观特征结构参数的表征，对导热性能与微观特征结构的关联性进行了研究。研究结果表明，碳纤维热导率随着石墨微晶的基面宽度（La）、堆砌厚度（Lc）和平均堆垛层数（N）的增大而增大，随着孔隙率（Vp）的增大而降低。基于Raman图谱的分峰拟合信息，对碳纤维的石墨化度进行分析。结果显示，碳纤维的石墨化度越大，热导率越高。

0 引言

碳纤维［1-2］具有高比强度、高比模量、热膨胀系数小、尺寸稳定等优点，成为重点研究的航天器结构承载材料［3-5］。近年来，碳纤维复合材料也逐渐向结构功能一体化方向发展，其导热特性获得极大关注，碳纤维热导率成为与力学参数一样重要的性能指标［6-8］。当前，虽然国内碳纤维生产技术取得了突破，但是结构-性能关系的讨论不多［9］，而有关碳纤维导热性能与微观特征结构的关联性更是缺乏系统研究。碳纤维的热导率取决于其微观特征结构，微晶、取向、微孔含量、石墨化度是影响纤维导热性能的关键因素。因此，本文主要通过XRD 和Raman 对碳纤维微观特征结构及石墨化结构特性开展研究，分析导热性能与微晶尺寸、微孔含量、石墨化度的关联性，以期为碳纤维研制开发及生产优化提供参考，也为碳纤维的质量控制和应用验证提供微观特征结构的检测分析途径。

1 试验

1.1 材料

国产某等级高强碳纤维（本研究中标注为：QCF-1），某等级高强高模碳纤维（两种，分别来自两个厂家，分别标注为：QMCF-1、QMCF-2）、另一等级高强高模碳纤维（两种，分别来自两个厂家，分别标注为：QMCF-3、QMCF-4）的聚丙烯腈基碳纤维，材料特征见表1。作为比对，实验研究材料还包括M46J、M50J碳纤维，本研究中标注为：M46J、M50J。

表1 材料特征1）Tab.1 The features for materials1）

1.2 分析及表征方法

采用密度梯度柱法测定计算获得密度（ρ），用差示扫描量热仪测试比热容（cp），对于碳纤维材料，采用捆绑成束形成小圆片试样，将碳纤维丝束平行排布于圆形固定器中，确保纤维无打捻、紧密排列，减少纤维间的间隙透光，夹紧后切除固定器外的纤维，磨抛试样，尺寸控制为Φ12.7 mm×（2～4）mm，如图1所示，并采用激光闪射仪（LFA 467）测试热扩散系数（α），通过如下公式计算得到热导率（λ）。

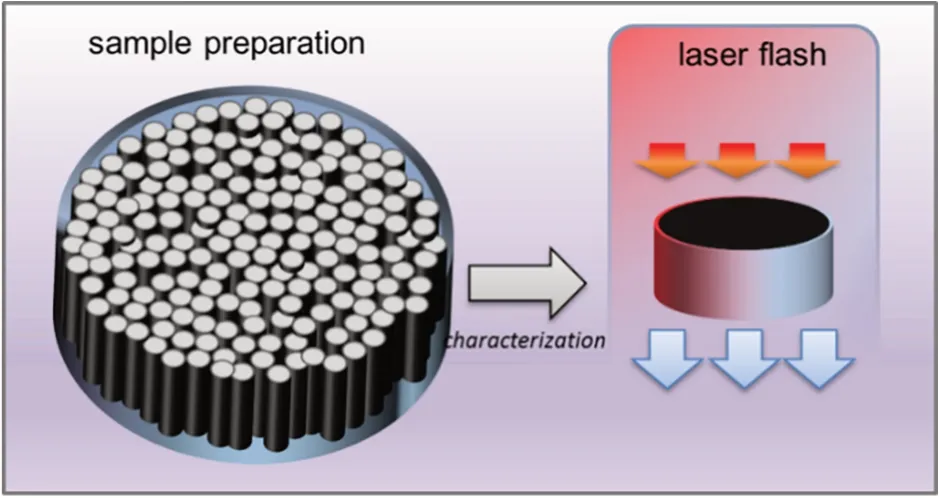
图1 碳纤维热扩散系数测试示意图Fig.1 Schematic illustration of thermal diffusivity coefficient of carbon fibers

采用X 射线衍射仪对材料进行相结构和微晶特性分析，采用Cu 靶辐射（Cu Kα辐射，λ=0.154 06 nm），2θ范围为15°～80°。采用拉曼光谱仪进行微结构及缺陷表征分析，拉曼位移范围：500～3 500 cm-1，激光器波长：514.5 nm。峰的积分强度使用Origin软件进行分峰计算。

2 结果与讨论

2.1 材料表征

采用X 射线衍射仪对碳纤维的微晶结构进行分析，QCF-1、QMCF-1、QMCF-2、QMCF-3、QMCF-4 碳纤维的XRD 图谱见图2。由图可看出，在2θ=25°附近出现代表（002）晶面的强衍射峰；在2θ=43°附近有一弱峰，归属（100）和（110）两个晶面的衍射。由于（100）和（110）两个衍射峰的位置十分接近，而碳纤维中微晶结构的不完善又造成两个峰的宽化，最终导致两者相互重叠为一个宽化的弱峰，习惯上称为（10）峰，可认为（10）峰由（100）和（110）峰叠加而成［10］。2θ=56°附近为（004）晶面的衍射峰，代表石墨微晶在C轴的发育程度，图谱显示，高强高模QMCF-3、QMCF-4 碳纤维微晶在C轴方向的发育程度更高。

图2 XRD图谱Fig.2 XRD patterns

进一步通过XRD图谱分析获取碳纤维的微晶层间距d（002）、微晶叠层厚度Lc、平均堆垛层数、孔隙率等微观晶体结构信息。晶面间距d（002）值和（002）峰的半峰宽β的大小能反映碳纤维石墨化程度的高低。d（002）值越小，β半峰宽越小，说明结晶性越好，石墨化程度越高。碳纤维的微晶参数由谢乐公式（Scherrer equation）计算。利用（002）衍射峰计算石墨微晶的层间距d（002）和石墨微晶堆砌厚度（Lc），利用（110）衍射峰计算石墨微晶的基面宽度（La）［11-12］，见公式（2）和（3）。

平均堆垛层数N由公式（4）计算。

碳纤维孔隙含量（Vp为孔隙率）由公式（5）［13］计算。

式中，θ为散射角，λ为X 射线的波长，K为形状因子，计算Lc时，K取值0.9；计算La时，K取值1.84［14］，β为衍射峰的半高宽，ρfiber为碳纤维的密度，ρg为天然石墨微晶的密度，其值为2.266 g/cm3，dg为天然石墨微晶的层间距，其值为0.335 4 nm［15］。

在碳纤维成型过程中，内部形成多层石墨结构，可以看出，通过碳纤维的微观结构分析表可看出（表2），高模量碳纤维相对于高强碳纤维，微晶层间距d（002）呈现降低的趋势，从QCF-1 到QMCF-3、QMCF-4 碳纤维，降低的最高幅度达到2.7%，且更接近于理想石墨晶体的层间距0.335 nm［16］。而堆砌厚度Lc和平均堆垛层数N呈现升高的趋势，升高的幅度均达到200%以上。基面宽度La同样呈现升高的趋势，升高的幅度达到200%～300%。结果表明，高模碳纤维生产过程中的高温处理促进了内部石墨微晶层的紧密收缩，微晶结构逐渐生长变厚。

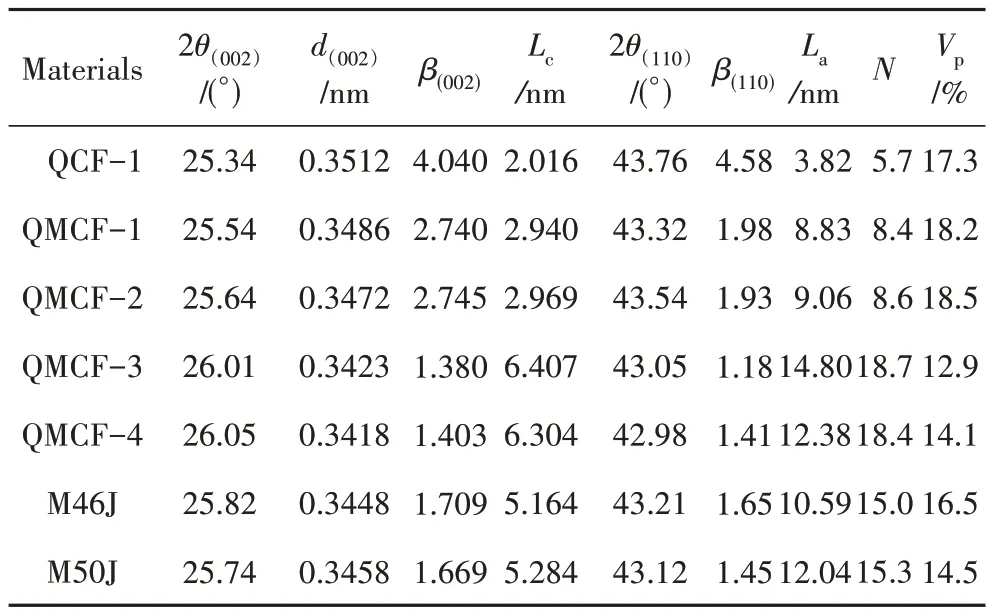
表2 微观结构参数分析表Tab.2 Microstructure parameters

如图3 所示，在低温升至高温过程中，碳纤维热导率随着温度的升高而逐渐升高。同时，从高强碳纤维到高模碳纤维，碳纤维的热导率逐渐升高，以大小排序为：QMCF-3＞QMCF-4＞QMCF-2＞QMCF-1＞QCF-1。

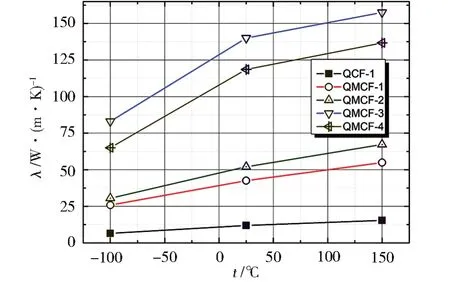
图3 不同温度下碳纤维的热导率Fig.3 Thermal conductivity of different carbon fibers at different temperatures

2.2 碳纤维热导率与微晶结构参数的关联性

碳纤维的热导率与微晶结构参数的依赖性关系：随着La的增大，热导率逐渐升高［图4（a）］；随着Lc的增大，热导率逐渐升高［图4（b）］；随着平均堆垛层数N的增大，碳纤维热导率逐渐升高［图4（c）］；而随着孔隙率Vp的增大，碳纤维热导率逐渐降低［图4（d）］。结果表明，提升碳纤维晶粒尺寸，降低微晶内部结构的孔隙率，均有利于碳纤维材料的传导热。

图4 碳纤维热导率与微晶结构参数的关系Fig.4 Relationship between the thermal conductivity and the microcrystalline structural parameters

碳纤维热量传导以声子传导为主，根据公式［17］：

式中，c为声子热容，vˉ为声子（晶格振动）平均速度，l为声子平均自由程。

图5为碳纤维微晶结构示意图，高模碳纤维与高强碳纤维的微晶结构的主要区别表现在：取向性更高，尺寸更大，层间结合更紧密。对于高强碳纤维，微晶结构中存在更多的贯通缺陷，孔隙分散在层间皱褶、位错等微位置，内部孔隙相对更丰富，同时在微晶边界存在更多的无定型碳结构［图5（b）］，对声子的散射作用增强，声子平均速度会更低。而对于高模碳纤维，晶粒尺寸变大［图5（c）］，增大了声子平均自由程。因此，高模碳纤维的微晶尺寸更大，层间更致密，孔隙率更小，导致声子平均速度和平均自由程更大。通过公式（6）可看出，其热导率越大。

图5 碳纤维结构示意图Fig.5 Schematic diagrams of carbon fiber structure

2.3 碳纤维热导率与石墨化度的关系

采用拉曼光谱仪对碳纤维微观结构的有序程度（石墨化度）进行检测分析。几类碳纤维的Raman 图谱如图6（a）所示，从图中可以清楚地看到1 360 cm-1附近的D 峰、1 580 cm-1附近的G 峰主峰信号。代表微晶结构中的边缘缺陷和不对称碳结构的D 峰，表征了类金刚石碳sp3电子结构的A1g联合振动模式，对应石墨片层的边缘碳和石墨微晶（纳米石墨）［18］。代表完整晶体结构的G 峰，表征了sp2电子结构的E2g联合振动模式，对应石墨片层的芳香环结构碳和有序碳［17］。1 500 cm-1左右的A 峰，主要由无定型碳或者某些有机官能团引起［19］。1 200 cm-1左右的D′′峰，在碳材料中可表征脂肪结构或类烯烃结构中碳-碳键的伸缩振动，以及类金刚石微晶结构的sp3键振动［20］。1 620 cm-1左右的D′峰，类似于G 峰，被认为是石墨微晶的E2g振动模式［21］。因此，通过Raman 图谱发现，碳纤维内部处于非晶碳与晶体碳（石墨微晶）共生、有序与无序共存的状态。

通常，D 峰与G 峰的积分强度的比率（ID/IG）与碳网平面上微晶的平面尺寸或无缺陷区域成反比关系，即ID/IG值越小，微晶越大，结晶越完整，石墨化度越高［22］。本研究中，综合考虑碳纤维的相结构的多样性及对导热性能的潜在影响，D′峰和G 峰积分强度和占所有峰的积分强度的总和的比值来表征碳纤维的石墨化度，即，若以gR表示石墨化度，则其表达式为：

通过Origin 软件，进行分峰拟合分析［图6（b）～图6（f）］，QCF-1碳纤维表现出较宽D峰和G峰，两峰谱线也存在多峰交叠，表明其微晶结构的不完善。从高强到高模碳纤维，D″峰和A 峰逐渐变弱，甚至消失；G 峰逐渐变强，且D′峰逐渐显现，D 峰、G 峰和D′峰变得尖锐，其微晶结构变得完善；而且，G峰峰位向高波数移动，说明高模碳纤维实现了更多的杂原子脱除，这是因为杂原子脱除的位置会形成空位，影响了碳网面内的共轭性，使振动能级差增大。因此，通过Raman 谱峰发现，在碳纤维材料中，高强碳纤维的边缘缺陷、sp3结构、无定型碳含量更高，而高模碳纤维的sp2结构、环状结构更多。Raman 图谱详细的分峰峰位、峰面积及石墨化度结果见表3。结果表明，相比于高强碳纤维，高模碳纤维的gR更高，即石墨化度更高，石墨化度依次排序为：QCF-1＜QMCF-1＜QMCF-2＜QMCF-4＜QMCF-3。

表3 Raman图谱信息分析表Tab.3 Structural information of carbon fibers via Raman

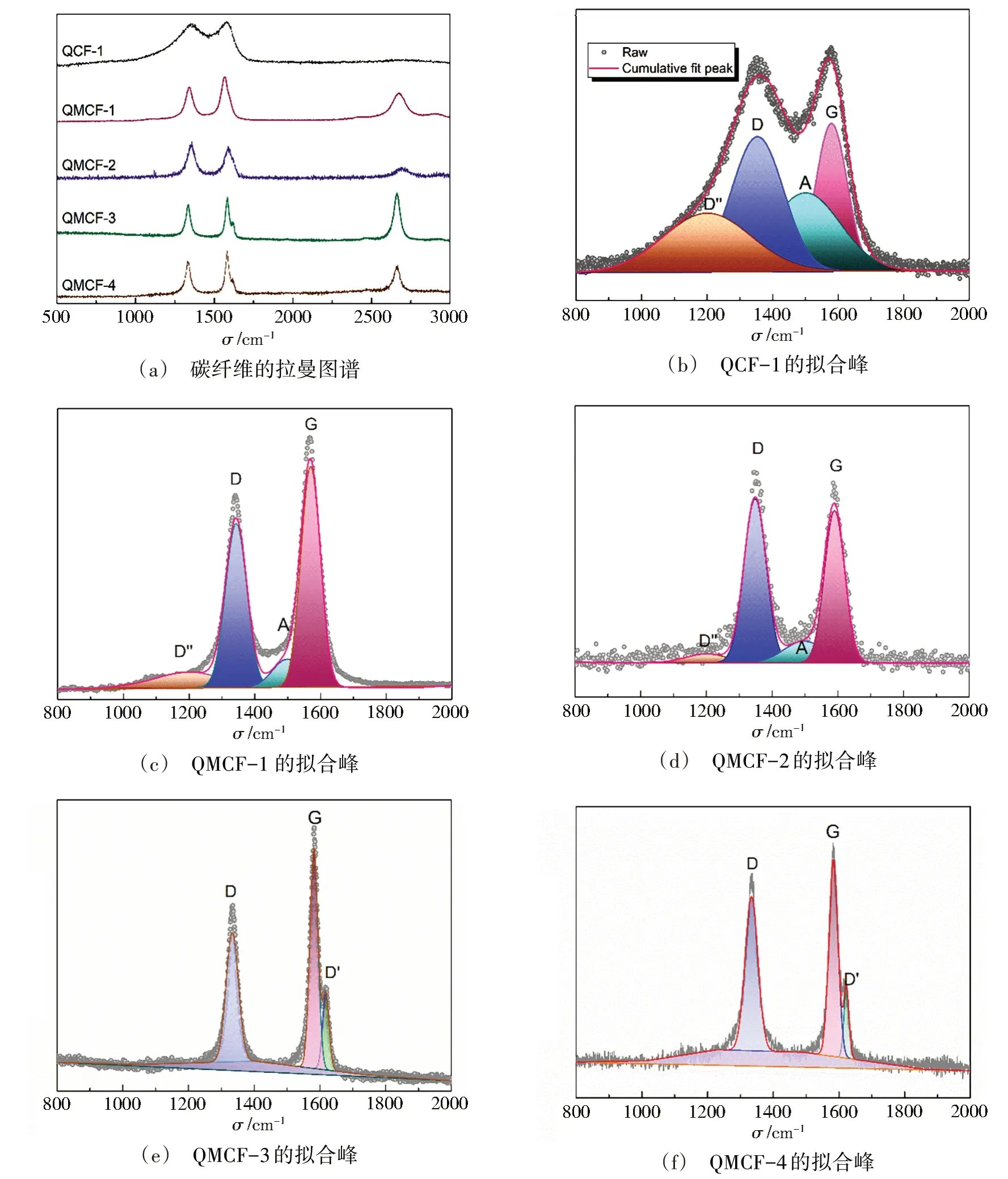
图6 拉曼图谱分析Fig.6 Raman analyses

碳纤维热导率与石墨化度的依赖关系如图7 所示。碳纤维的石墨化度越大，热导率越高。碳纤维中的空位、杂原子等缺陷均会对石墨化度造成影响，因而在碳纤维性能调控中，减少空位、杂原子和结构缺陷均有利于提升材料的导热性能。

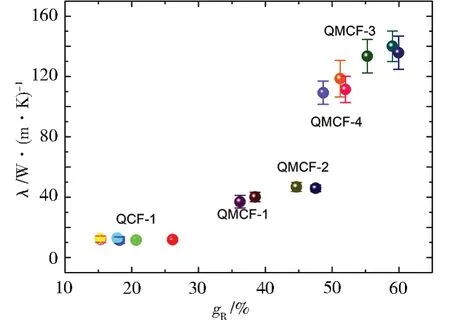
图7 热导率-石墨化度的关系Fig.7 The relationship of thermal conductivity of the carbon fibers and graphitization degree

3 结论

（1）通过XRD研究发现，碳纤维热导率与材料微观特征结构参数紧密相关，其随着石墨微晶的基面宽度（La）、堆砌厚度（Lc）和平均堆垛层数（N）的增大而增大，随着孔隙率（Vp）的增大而降低。

（2）从声子传导机制解释了热导率与微观特征结构参数变化规律的原因：微晶尺寸越大，层间越致密，孔隙率越小，导致声子平均速度和平均自由程越大，热导率越大。

（3）通过Raman 研究发现，碳纤维的石墨化度越大，热导率越高。

该研究结果可指导碳纤维材料的性能调控和优化、质量控制和应用验证。