风光水互补发电自动发电控制模型及仿真研究
五凌电力有限公司三板溪水电厂 龙海军
1 引言
当前,以风电和光伏发电为代表的新能源的应用范围仍在不断拓展,但这些发电模式存在着输出波动性强和输出功率不可预测等问题,给整体电力系统的安全稳定运行造成较大影响。为规避此类问题,基于风电、光伏发电和水电的互补性特点,将其视为一个整体,打造“风光水互补”的发电模式就成为值得研究的一项内容。在本项研究内容中,关键点则需要构建行之有效的控制模型,对各种要素的优化调度,解决非线性复杂问题,需要进一步的探究。
2 整体架构设计
风光水互补发电系统属于一种较为复杂的系统,包括风电场、光伏电站、水电站和抽水蓄能电站等主要部分。风光水互补发电系统整合了风力发电、光伏发电和水力发电等3 个主要模块,风光水互补发电系统主要特点是能够充分利用风电和光电的天然互补性;具备水力发电优良的稳定性和调节性能,能够有效降低间歇性电源并网给电网造成的冲击。风光水互补发电系统中自动发电控制模型的关键是在满足电力系统及多种电源特性约束的前提下,以水电站调节为核心,在一定程度上削减负荷峰谷差,确保调节能力较差的风电和光伏发电在剩余负荷上尽量保持平稳,确保电网的平稳运行。为达成这一目标,本研究基于经典控制理论PID 控制理论,并应用Simulink 软件构建风光水互补机组模型[1-2],对本模型进行分析,以寻求其控制策略的优化,进而确保电力系统的稳定运行。
3 风光水互补发电自动发电控制模型的建立
3.1 水电机组的建模
本研究考虑到水电机组的结构相对较为复杂,因此从以下几个方面分别进行建模操作。
一是针对水轮机系统进行建模,在水电机组的实际运行过程中,本模块的主要作用是,通过调节水流量实现水轮机的调速,从而间接实现调节发电功率的作用。因此,重点对水轮机调速系统进行分析建模。本系统中,调速模型又可细分为水轮机调速器PID 调节模型和液压系统模型。其中,微机调速器PID调节器的输出应用如式(1)所示:
式(1)中,YP表示PID调节器调节输出的比例分量;YI为积分分量;YD为微分分量。
在PID 调节器输出控制信号后,经过液压转换器变更为液压信号,再经过引导阀和主配压阀逐级放大,最后推动主接力器动作,带动水轮机导叶的开启或关闭。根据已有的研究经验,水轮机组的出力动态方程如式(2)所示:
在式(2)中:At表示水轮机增益,该参数通常为常数项;h为水轮机水头高度;q是流量的偏差值;Pm是输出机械功率的相对值;qnl是空载流量相对值;Δω表示机主角速度的偏差值;Dt是阻尼因子;y是接力器行程的相对值。接力器行程与导叶开度之间存在线性关系,二者的绝对值也是相等的。
二是对发电机模型进行建模,基于本软件内置的DQ 转子参考框架,进行三相同步电机的建模。其中,定子绕组以Y 型连接至内部中性点。同步机组在发电机或电机模式下运行,在电机的电气部分,则采用六阶状态空间模型,六阶发电机模型采用Simulink软件中已有的同步发电机模块。模型考虑了定子、磁场和阻尼绕组的动力学特性。同时,模型的等效电路以转子参考框架(QD 框架)予以表示,从定子上即可以查看所有转子参数和电气量。
三是针对励磁模块的选型,本模块直接在Simulink软件中选择适合本次研究的一类模块,由电压调节器和励磁机组成励磁系统模块。
3.2 风力发电机组系统建模
基于本次研究的实际需要,在风力发电机组建模环节中,研究人员首先将风电场的功率确定为9MW,在本风电场中,主要以双馈感应发电机(简称为DFIG)为核心,并以涡轮机加以驱动。在本风力发电场的设计中,研究人员在Simulink软件内共选择1.5MW 的风力涡轮机模型6 个,将其进行组装,模拟本次所需的9MW 风电场,再将其连接到构建规格为25kV的配电系统,长度为30km的馈电线路,向电网输出电力。采用双馈感应发电机的风力涡轮机可以细分为绕线转子感应发电机和基于AC/DC/AC/IGBT 的PWM 变换器组成,定子绕组直接连接到50Hz 电网,而转子则通过AC/DC/AC转换器,以变频模式进行供电[3-4]。
3.3 光伏发电并网系统建模
基于本次研究的实际需要,在光伏发电并网系统建模环节中,研究人员选用五参数模型的光伏阵列块,以此为核心进行建模。在本模型的设计中,为充分体现光伏发电的特性,主要包含电流源(光产生电流)、二极管、串联电阻、分流电阻。同时,为兼顾特殊情况,在本次设计的模型中增设了逆变器模块。在此基础上,结合既有的研究经验,本次模型选择基于扰动观测算法的MPPT控制器来实现。
3.4 风光水互补发电模型的建立
在所有发电系统模型选择完成后,将光伏发电、风力发电和水力发电机组模型以一定的距离连接到电力系统中,形成风光水互补发电模型。研究人员基于此模型,对系统控制参数的优化展开研究。
4 仿真分析结果与讨论
在不同容量配比下,PID 参数对整体电力系统的影响均相似,因此在仿真分析过程中,确定容量配比为风力发电∶光伏发电∶水力发电=40∶1∶150,在此情况下,探究比例系数、微分系数和积分系数对系统稳定性带来的影响[5]。在研究过程中,风光水互补发电系统的稳定性函数如式(3)所示:
式(3)中,R(s)表示等效函数;K表示可调节的增益;G(s)为反馈通路系统函数;H(s)是正向通路系统函数。据此,通过对不同参数分别进行调整来分析系统的稳定性,从而得出较优的控制参数。
比例系数需要进行调整,系数从0.8 开始,以0.4 为步长,最终增加到2.4,分别分析在不同比例系数下的系统的奈奎斯特响应结果,如图1所示。
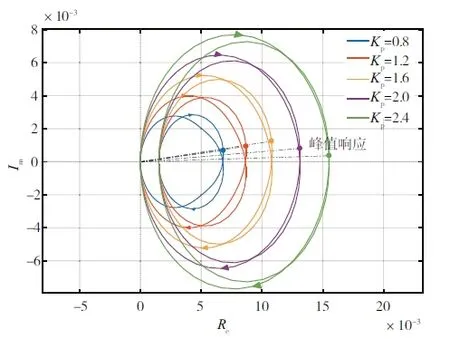
图1 不同比例系数下系统的奈奎斯特响应结果
由图1 可知,在不同比例系数下,系统的奈奎斯特响应曲线整体走势相似,曲线均从原点出发,向右上延伸,按照顺时针方向环绕两次回到原点,第一次越过实轴后,奈奎斯特曲线的曲率变大,然后继续延伸,再次越过实轴后,曲率开始逐步减小,最终延伸回原点,形成一条上下对称的闭合曲线。曲线的峰值响应与比例系数呈正相关。根据奈奎斯特稳定性判据可知,当曲线环绕-1/K点的净次数为0 时,系统保持稳定,而以上曲线均符合判据,因此在比例系数变更过程中,系统均保持稳定。
积分系数的变化情况需要进行仿真分析,保持其他两个参数不变,将积分系数从0.25 开始,以0.25 为步长,逐步增加到1.25,不同积分系数下的系统的奈奎斯特响应如图2所示。
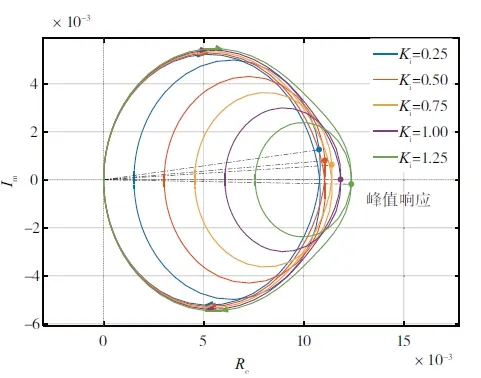
图2 不同积分系数下的系统的奈奎斯特响应
由图2 可知,积分系数的增加对于系统奈奎斯特响应曲线的整体走向影响并不显著,奈奎斯特曲线仍基本保持上文中的走势,从原点出发,向右上延伸按顺时针方向环绕2 次回到原点。其中,曲线第一次越过实轴后,奈奎斯特曲线曲率变大,而第二次越过实轴后奈奎斯特曲线曲率则变小,最终延伸回到原点,使奈奎斯特曲线具备上下对称且闭合的特性。同时,随着积分系数的增大,系统奈奎斯特响应的峰值也随之提高,积分系数对系统的稳定性影响不突出,在调整积分系数的过程中系统均保持稳定。由此可知,超调量处于系统稳定的范围内,系统的超调量随着积分系数的增大而增大,结果显然,如增大积分系数,系统将具有更优的动态特性。
对系统的微分系数的影响进行仿真分析。保持其他两个PID参数不变,将微分系数从0.5开始进行调整,步长设置为0.25,逐步将微分系数增加到1.5,分析微分系数的变化对系统的奈奎斯特相应造成影响,不同微分系数下的系统奈奎斯特响应曲线如图3所示。
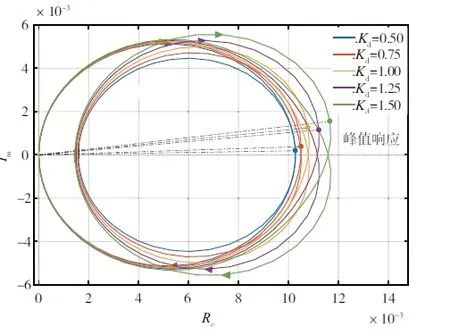
图3 不同微分系数下的系统奈奎斯特响应曲线
由图3 可知,随着微分系数的增大,系统的奈奎斯特响应曲线仍保持基本相同的走向趋势,从原点出发,向右上延伸按顺时针方向环绕两次回到原点。其中,曲线第一次越过实轴后,奈奎斯特曲线曲率变大,而第二次越过实轴后奈奎斯特曲线曲率则变小,最终延伸回到原点,使奈奎斯特曲线具备上下对称且闭合的特性。
综合分析以上几条奈奎斯特曲线可知,所有的奈奎斯特曲线在实轴上只相交于原点,曲线靠近原点的另外一半随着微分系数的增大向右移动,但这种向右移动的趋势不显著,且随着微分系数的增大,曲线的曲率反而呈减小趋势,这种变化对于奈奎斯特峰值响应的增加并未造成影响,系统也仍然保持相对稳定的状态。
结合以上仿真分析步骤可知,在超调量处于系统稳定范围内时,奈奎斯特曲线的峰值响应情况与微分系数呈现正相关,因此系统超调量也与微分系数呈正相关,在增大系统微分系数后,系统的动态特性也将得到改善。
5 结语
本研究基于Simulink 软件对风光水互补发电系统模型进行了初步的建立,并进行仿真分析,结合其奈奎斯特曲线变化情况可知,当确定风光水发电的容量配比后,增大比例系数、积分系数和微分系数均能够提升系统的动态特性。同时,积分系数的增大能够提高系统的快速性,而比例系数和微分系数的增大则会降低系统的快速性。如何对这3 个系数进行优化调整,以兼顾系统的快速性和整体性能,将成为后续研究中需要进一步探究的内容。

