地质统计学在红牛铜矿山模型研究及储量计算的应用

张春元，李建翔，王 杨

(云南黄金矿业集团股份有限公司，云南 昆明 650200)

地质统计学自二十世纪七十年代发展至今，被广泛运用于矿床勘查、开采过程中储量计算及误差分析中。以区域化变量为基础，以变异函数为模型，定量研究随机变量在空间的变异性，并用协方差函数矩阵表征相关性，通过求解线性方程组完成空间插值，是一种无偏、最优的估计方法[3]。本文使用GeoviaSurpac矿业软件对云南省红牛铜矿KT2-1矿体，从理论和实践上阐述了地质统计学在矿体资源储量估算中的应用，通过实践证明，运用地质统计学进行矿体资源储量估算和传统资源储量估算方法相比具有较大的优越性。

1 地质概况

矿区位于迪庆州香格里拉市区19°方向平距约40km处。大地构造位置地处甘孜-理塘结合带西侧德格-中甸陆块东缘，印支期义敦-中甸岛弧带南段，总体近北北西向展布。矿区出露第四系全新统松散堆积层(Q4)，三叠系上统图姆沟组(T3t)、曲嘎寺组(T3q)。构造主要为褶皱和断裂构造。褶皱轴向以北北西向及近南北向为主，断裂构造有北西向、北东向及东西向三组断裂。岩浆岩为浅成中酸性侵入岩，岩性为闪长玢岩(δμ)、石英闪长玢岩(δομ)，局部石英二长斑岩(ηομ)。均与本区铜、钼矿化关系密切。特别是石英二长斑岩具较强铜、钼矿化(斑岩型铜、钼矿)，围岩接触带具矽卡岩化，形成矽卡岩型铜矿。矿区内变质作用类型主要有区域变质作用、接触(交代)变质作用两类。与成矿有关的主要是接触(交代)变质作用。

该矿床以铜为主，同体伴生银、硫矿产的中型铜矿床。属与印支-燕山期中酸性浅成-超浅成斑(玢)岩侵入有关的矽卡岩型矿床，矿体主要赋存上三叠统曲嘎寺组二段二亚段(T3q2-2)中，赋矿层位为大理岩/角岩岩性分界面矿化层位和大理岩矿化层位。矿化带空间展布基本与矿区地层、主构造线大致平行排列展布。

本文以KT2-1矿体为估算对象，走向长701.60m，倾向斜深68.44m～529.70m，控制标高3601.49m～4208.80m，相对高差607.31m[1]。矿体赋存于层间破碎带旁侧条带状角岩中，总体呈北西-南东向展布，呈脉状产出，厚度1.04m～26.56m，平均5.37m，矿体Cu品位0.31ω%～14.38ω%，平均0.73ω%，三维形态见图1。

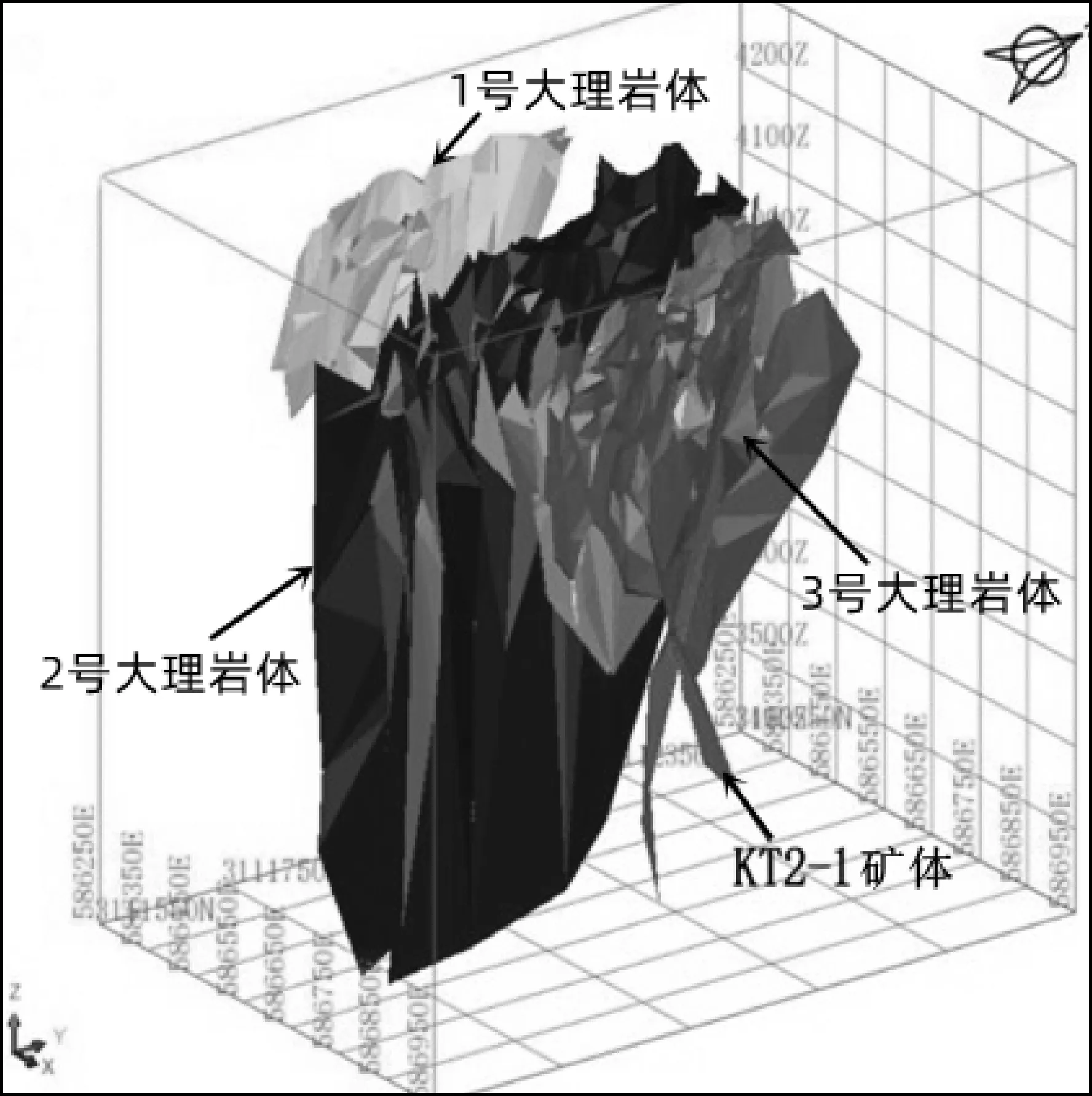
图1 红牛铜矿KT2-1矿体模型示意图Fig 1.Schematic Diagram of KT2-1 OrebodyModel of Hongniu Copper Deposit

2 资源储量估算

应用地质统计学(普通克里格法)资源储量估算流程见图2。

2.1 建立地质数据库

将原始的数据：工程定位、工程测斜、样品化验结果及岩性记录以表格形式记录，直接导入数据库系统，建立地质数据库。

2.2 建立矿体实体模型

实体模型建立原则是运用一系列三角面构建成完整的矿体轮廓，可将矿体三维可视化显示，矿体形态直观，能便捷的提取矿体的体积、赋存标高、埋深等信息[4]。具体步骤：(1)整理矿区勘探线信息文件；(2)生成勘探线剖面图，并完成勘探线剖面图上矿体圈定及地质信息解译；(3)生成矿体实体模型，将相邻剖面的矿体三角面连接起来，围成一个复杂曲面的矿体实体模型。

2.3 样品基本统计分析及特异值处理

采用地质统计学资源量估值前，需要对矿区样品数据统计(表1)，统计矿体的样品数量、平均值、自然对数平均值、几何平均值、对数方差、西舍尔系数与西舍尔估值等数据，若平均值>西舍尔估值，则说明该矿体存在特异值(特高品位)，应处理。依据国内外实际建模经验和国际通用惯例，通常取品位累积分布曲线97.5%所对应的品位值作为特异值下限值。

特异值处理方法采用将样品品位高于特异值下限的部分去掉，用特异值下限值替代特高品位值。然后继续采用西舍尔估值检验法对处理结果判别，若平均值≤西舍尔估值，则说明处理结果合理(表2)，否则重复上述步骤继续处理，直到符合要求为止。

本次KT2-1矿体的特异值处理次数1次，最终确定Cu特高品位下限3.18%。

表1 KT2-1矿体样品特征统计表

表2 特异值合理性检验表

2.4 样品等长度组合

组合样品就是将空间不等长的样长和品位量化到一些离散点上，只有在工程方向上产生等支撑的离散点，才用于资源储量估算[5]。样品组合时，采用样长加权平均法。通过统计KT2-1探矿工程(图3)，样长绝大多数为1.0m(样品数895件)，组合长度定为1.0m，能保证绝大多数样品信息保持不变。通过对比(表3)，样品等长度组合后，样品数量虽大幅增加，但Cu品位最小值、最大值、均值、中值近乎一致，方差、变化系数适当减小，符合矿区实际，本次核实组合样长选择为1.00m是合理的。

表3 KT2-1矿体Cu品位组合前后对比结果表

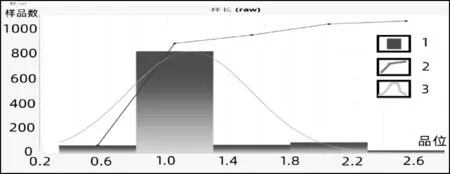
图3 KT2-1矿体样长特征图

2.5 变异函数模型建立及分析

本次选择KT2-1矿体采用普通克里格法在估值前必须使用变差图模型(球状模型)进行试验变异函数研究[6]，得到普通克里格法估值赋值所必需的搜索椭球体的方位角、倾伏角、倾角、主轴与次轴之比、主轴与最小轴之比以及试验变异函数的块金值、基台值、变程等参数。

(1)全方向变差图：首先360°全方向的形成矿体Cu品位的变差图(图4)，通过微机交互地调整“块金值、基台值、变程、滞后距”等参数对变异函数的理论曲线在屏幕上进行拟合。得到矿体KT2-1全方向Cu品位变异函数的参数：块金值(NUGGET)=0.075，基台值(SILL1)=0.192，变程(RANGE1)=6.400，滞后距(LAG)=1.0。

(2)主轴方向变差图：KT2-1矿体总体倾向243°，倾角80°，首先对矿体空间形态的理想平面上做Cu品位主轴方向变差图(图5)，通过对变异函数的理论曲线拟合，得到主轴方向327.2°、倾伏角29.8°矿化连续性最好。得到KT2-1主轴方向Cu品位变异函数参数：块金值(NUGGET)=0.075，基台值(SILL1)=0.192，变程(RANGE1)=240.000，滞后距(LAG)=43.0。

(3)次轴方向变差图：随后计算得到次轴方向变差图(图6)，次轴所在平面与主轴垂直，再次拟合，得到次轴方向327.2°、倾伏角-60.2°矿化连续性最好。得到KT2-1次轴方向Cu品位变异函数的参数：块金值(NUGGET)=0.075，基台值(SILL1)=0.192，变程(RANGE1)=225.000，滞后距(LAG)=37.0。

(4)最小轴方向变差图：做出最小轴方向的变差图(图7)，最小轴所在的平面同时与主轴、次轴垂直；再次拟合，得到最小轴方向57.1°、倾伏角-0.2°矿化连续性最好。得到矿体KT2-1最小轴方向Cu品位变异函数的参数：块金值(NUGGET)=0.075，基台值(SILL1)=0.192，变程(RANGE1)=37.600，滞后距(LAG)=14.5。

通过上述对矿体的各方向的变异函数的计算及曲线的模拟，可以确定KT2-1矿体的Cu品位变异函数具有几何异向性，空间各方向的变程构成了各向异性椭球，其方位角327.2°；倾伏角29.8°；倾角89.8°，Cu品位变异函数理论模型参数见表4。

表4 KT2-1矿体Cu品位变异函数理论模型参数表

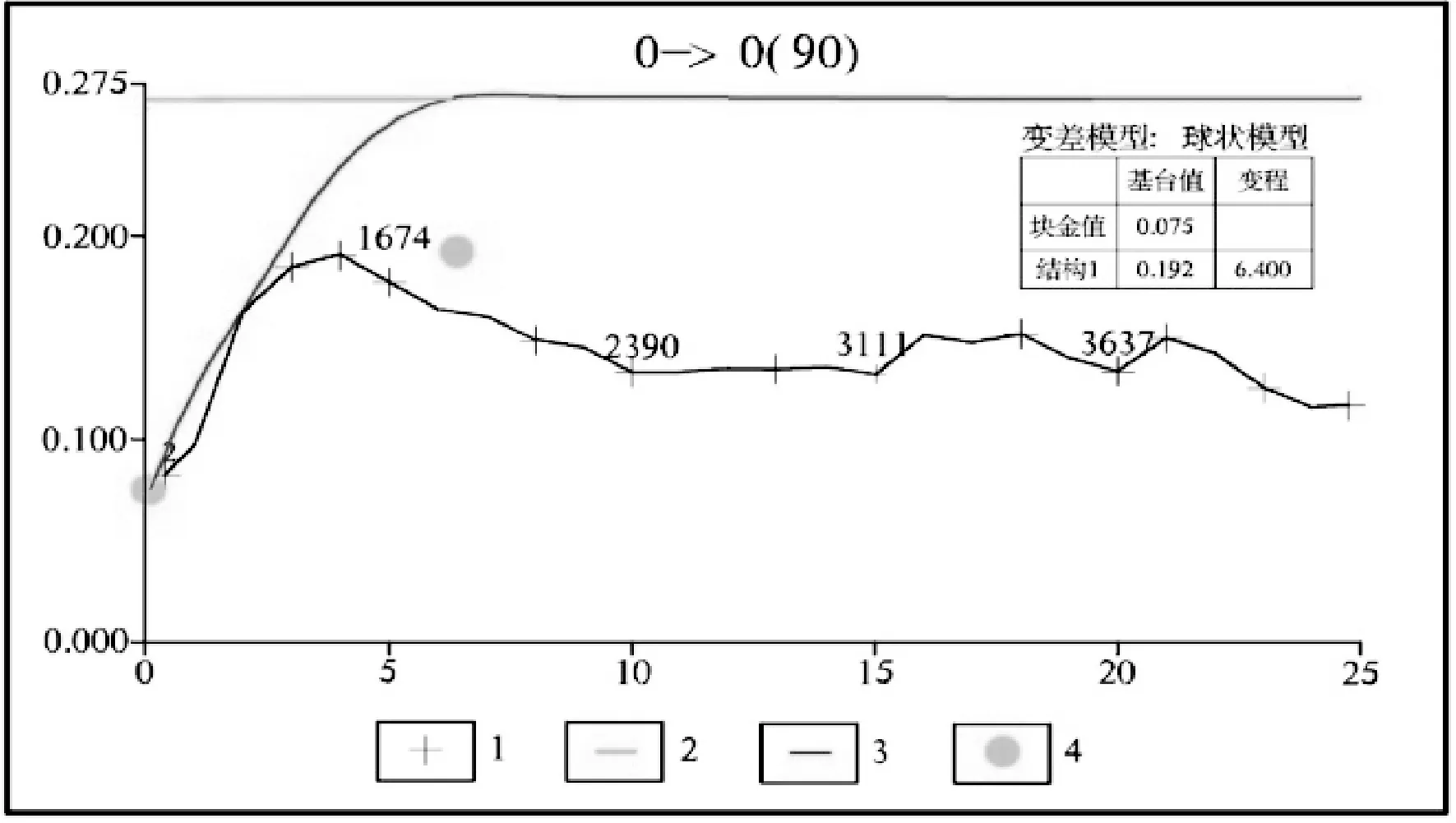
图4 KT2-1 Cu品位全方向变差图Fig 4.Cu Grade Variation Diagram of KT2-1 Ore BodyinAllDirections

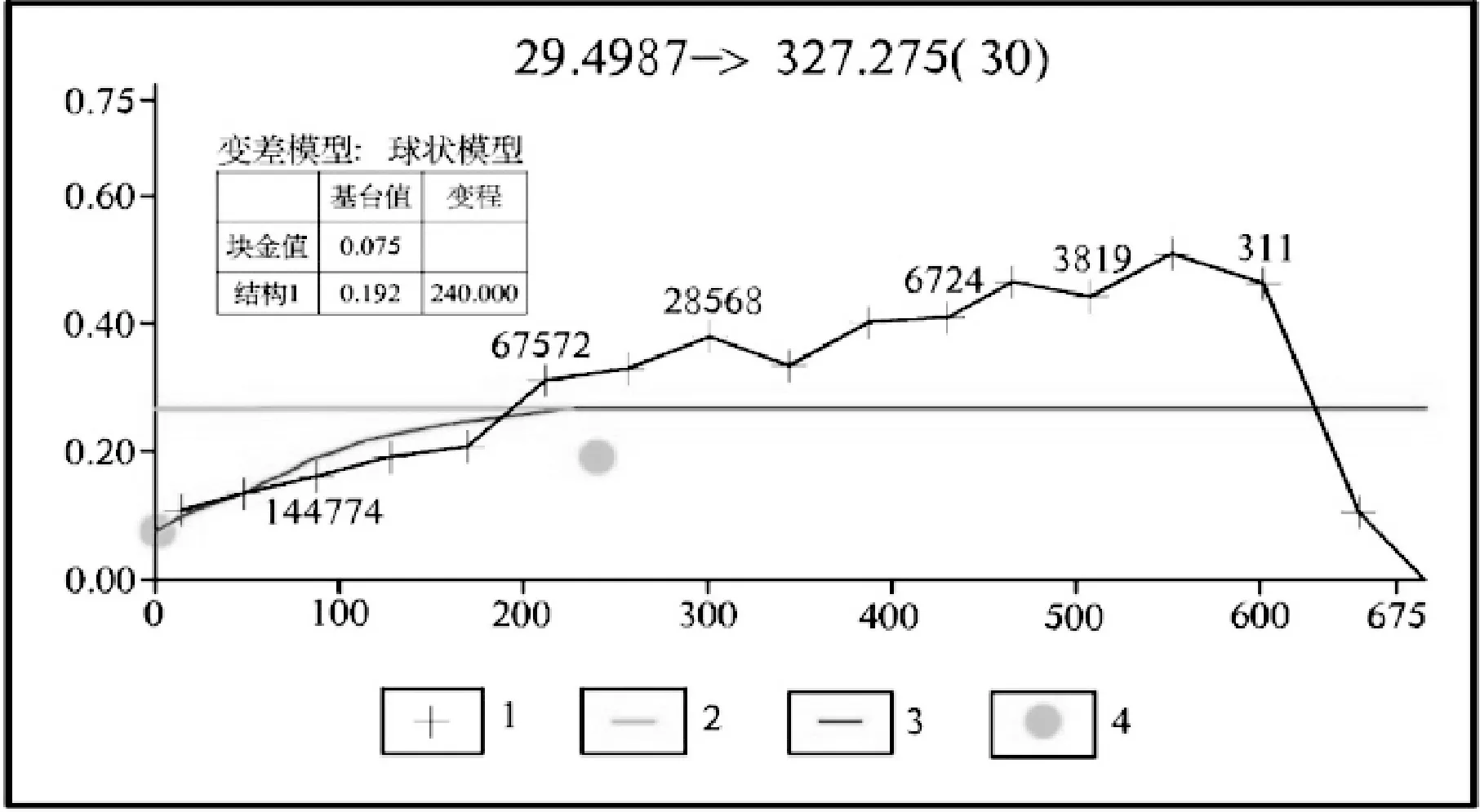
图5 KT2-1 Cu品位主轴方向变差图Fig 5. Cu Grade Variation Diagram of KT2-1 Ore Body in Main Axis Direction

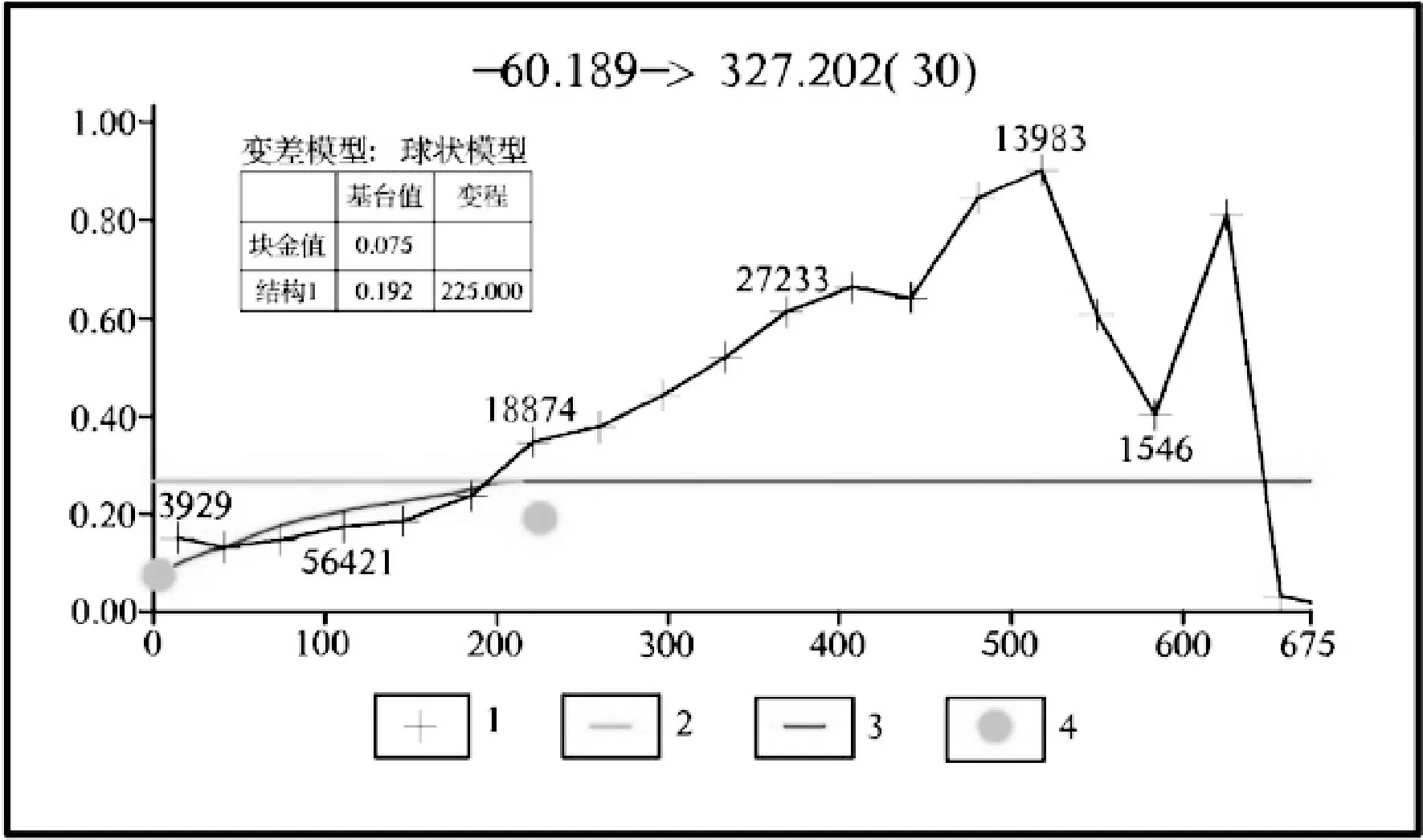
图6 KT2-1 Cu品位次轴方向变差图Fig 6. Cu Grade Variation Diagram of KT2-1 Ore Body in Sub-Axis Direction

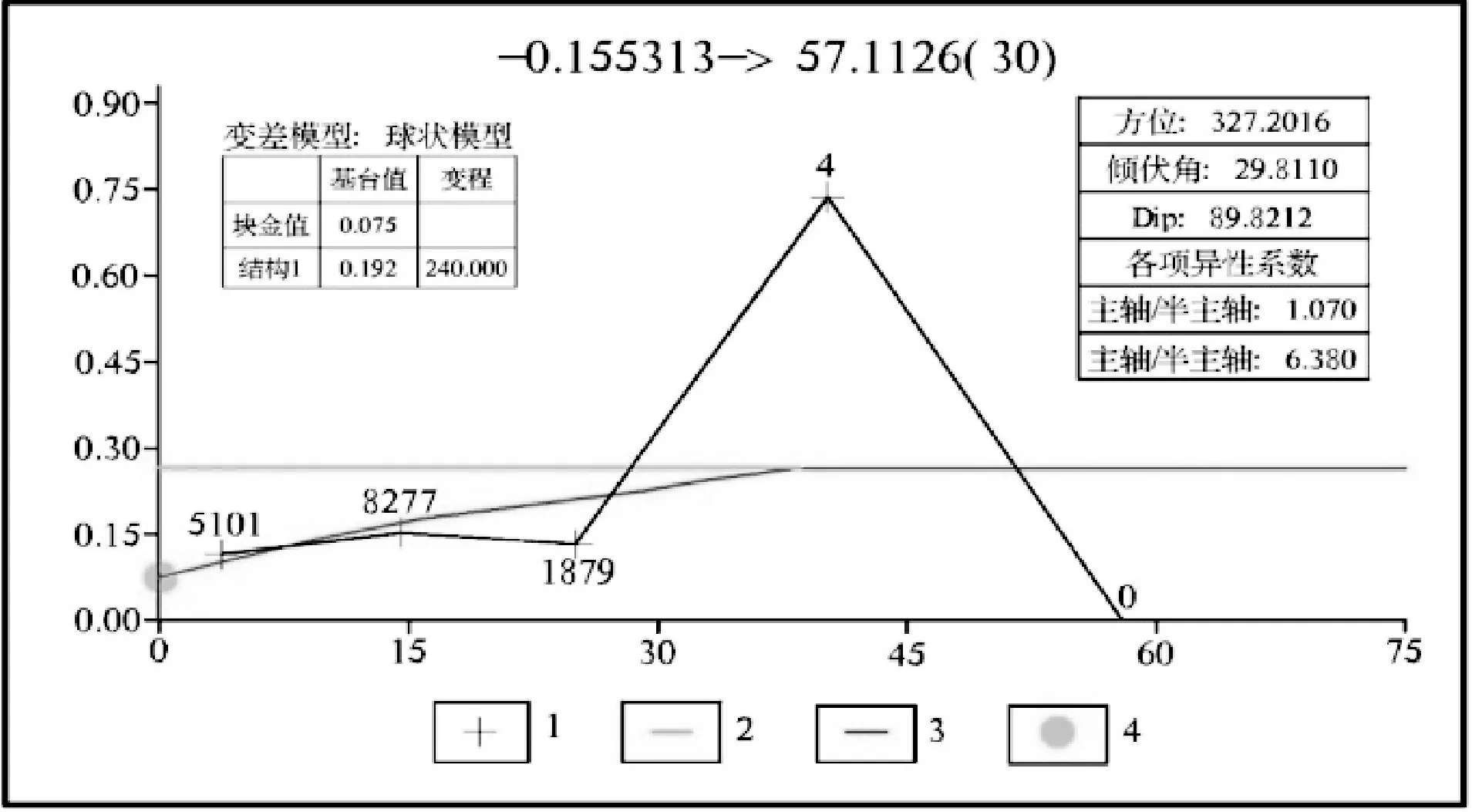
图7 KT2-1 Cu品位最小轴方向变差图Fig 7. Cu Grade Variation Diagram of KT2-1 Ore Body in Minimum Axis Direction

2.6 交叉验证

用交叉验证的方法对普通克里格法估值参数验证，即对每一个Cu元素特高品位处理后组合样品的实际空间位置用拟合理论变异函数进行估值，得到每个点的克立格估计值和克立格估值理论方差，用每个点的克立格估计值与该点的实际值进行相减，得到每个点的克立格估值误差，并进行统计，可得估值误差均值和方差，根据误差的均值、方差和每个点估值时克立格理论方差的均值，判定拟合的变异函数模型合格与否，合格的变异函数模型应该满足以下条件：(1)克立格估值误差的均值接近于0；(2)克立格估值误差的方差与克立格估值理论方差的均值相对误差在15%之内，二者均值之比接近1；(3)大约有95%克立格估值误差落在±2倍的克立格估值误差的方差区间内。

表5 KT2-1矿体Cu品位交叉验证结果表

根据模型参数对组合样品中每个数据点用普通克立格方法对Cu品位值进行估值，通过调整变异函数的结构参数，将块金值(C0)调为0.182，基台值(C1)调为0.085时，模型符合要求。

通过验证计算(表5)，克立格估值误差平均值较小趋近于0；克立格估值误差方差与克立格估值理论方差均值之比为1.0311，接近1；估值误差落在±2倍克立格估值误差方差内百分比大于95%；满足普通克立格法估值精度要求，本次核实KT2-1矿体Cu品位最终参与估值赋值的变异函数模型符合要求。

2.7 建立矿块模型

块体模型是矿床品位估计及资源储量估算的基础。把矿体空间分布范围划分为小长方体块进行品位插值，根据勘探线距、中段高差及矿体形态复杂程度确定块尺寸的大小，通常应使勘探线距、中段高差为块大小的整数倍[7]。矿区勘探线距25m、段高12m，矿体形态复杂程度为复杂，产状较陡。块体模型基本块尺寸5m×5m×2m，当矿体厚度较小，厚度和品位变化较大时，划分子块尺寸1.25m×1.25m×0.5m，子块尺寸保证矿体空间实体模型边界的误差最小。

2.8 普通克立格法估值

估值就是求出块模型中每个块中心位置的品位值，就需要在具有相关性的空间范围内搜索已知点，并通过给予一定的权系数实现“最佳、线性、无偏”估计。根据变异函数模型与交叉验证结果，将第一次估值椭球搜索的主轴半径定义为矿体“探明的”勘查工程网度75m(走向方向，理论网度1.25倍)估值。对不满足第一次估值搜索椭球条件的矿块，通过依次改变搜索半径为第一次搜索半径的2倍、4倍的方法继续进行第二次、第三次估值(表6)。矿体KT2-1工程控制程度高，样品密度大，三次估值完成后所有的块模型都估算出了Cu品位。

表6 KT2-1矿体普通克里格法估值样品数量约束情况表

3 可靠性验证

资源储量估算结束后经过验证，用普通克里格法估算资源量与垂直纵投影块段法估算资源量对比(表7)，合计金属量误差为0.16%。结果表明：本次采用的资源储量估算方法以及相对应的参数选择是合理、正确的，结果可靠性强。

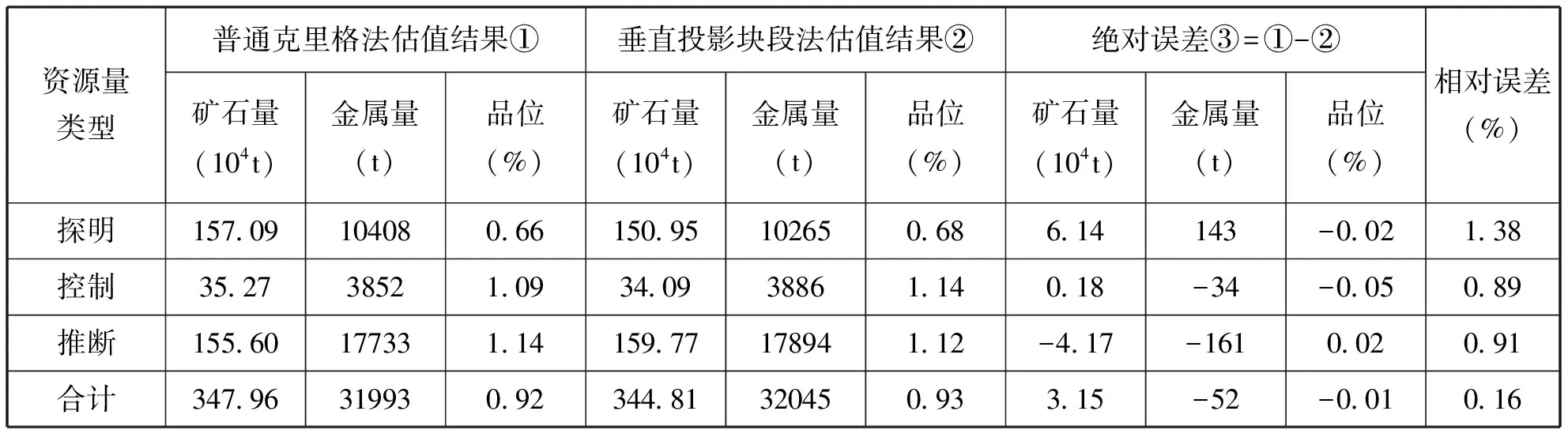
表7 KT2-1矿体普通克里格法与垂直纵投影块段法估算结果对比表

4 存在问题探讨

(1)数据的录入需严格进行数据校验，如样品跨层、岩性分层重叠，测斜、取样、岩性深度超出终孔深度，探矿工程坐标核实等。

(2)矿体实体模型建立过程中需综合考虑地层因素、控矿、破矿构造等，需要严格的按照地质勘查规范要求对计算软件进行人工干预。

(3)矿体实体模型绘制中，一定要避开非见矿工程及夹石的剔除，真实反映矿体形态，否则对估值造成不准确的影响。

(4)估算结果的可靠性验证，除对比验证，还需野外实地核实。

5 结 论

本次对红牛铜矿KT2-1矿体模型建立合理，变异函数值的选取正确，所选用估值方法可行，资源量估算结果真实可靠。相比于其他估算方法，工作量简化，应对矿床工业指标随市场、技术革新等变动时，能最快的重新统计估算结果。与矿山实际生产结合更紧密，更有效地指导生产。