基于分时电价与储能充放电策略的台区可调控资源聚合及调度

汪 锋，刘智强，张克勇，王冠瑞，殷红德，贾子昊，赵海辉，米 阳

（1国网平顶山供电公司，河南 平顶山 467002；2上海电力大学电气工程学院，上海 200090）

随着电价改革、电能替代以及用户对高质量供电的要求，配电网安全稳定运行面临着巨大挑战[1]。为加快新型电力系统建设，低压配电台区网格化供电服务得到有效推进。近年来，“配电物联网”概念的提出，为配电台区有效管理提供了新颖的思路[2]。如何构建新型电力系统下配电台区管控架构，将配电台区打造成由“生产主导”向“服务主导”转变的智能决策者，是当前需要重点考虑的问题[3]。

在区域电力系统层面，尤其是配电网和台区层面，实现对台区不同类型用户可调控资源的用能管控，是提高台区运行稳定性、经济性以及可再生能源消纳比例的重要手段。国内外许多学者对用户侧可调控资源的合理挖掘与有效聚合已有了相关研究。文献[4]对空调模型进行聚合，分析空调聚合功率与室内外环境等参数的关系。文献[5-7]将热水器工作模式用0-1 描述，构建热水器负荷聚合模型并分析其聚合有效性。文献[8-10]基于不同类型电动汽车的起始荷电状态及起始充电时间建立了一定数量的电动汽车充电功率聚合模型。然而，以上研究均是针对单个同一类型的负荷进行的模型聚合，不适用于台区负荷多样性的特点。针对多类型的可调控资源，文献[11]引入负荷聚合商概念聚合各类用户负荷，并以经济性成本最优进行优化。文献[12]考虑用户用能满意度建立可调控资源物理动态模型，并建立了多级聚合算法。目前，对台区用户侧多类型资源的聚合及调度研究较少，未能给台区有效用能管控提供合理的思路。

随着大数据技术及智能控制技术的发展，需求侧响应主体群调群控策略越来越受到学者的关注。文献[13-14]计及风电不确定性制定了多时间尺度的价格激励型需求响应负荷调度策略。文献[15]计及需求响应不确定性，考虑消费者心理建立了以经济性成本最优为目标的多时间尺度的负荷调度模型，并分析其在削峰填谷作用方面的有效性。新型电力系统背景下，仅考虑单个不同类型负荷的优化调度已无法满足实际需求，需进一步研究一定数量的负荷聚合模型在系统、市场和用户多方利益竞争下的调控策略。

综上所述，为提高配电台区对用户侧可调控资源的管控能力，本工作基于配电物联网“云-边”协同技术搭建了包含感知层、网络层、应用层的台区用户侧用能管控系统框架，根据可调控资源响应不确定性将台区典型可调控资源分为电动汽车、温控负荷及分布式储能三种类型并对其进行功率聚合，进而计及分时电价与分布式储能充放电规则，建立包含用户用电成本及用能舒适度为主体的目标函数，最后采用差分进化算法迭代寻优并通过算例仿真证明所设计的负荷聚合模型及协调调度策略在调控潜力等方面的有效性。

1 配电台区用能管控系统框架

大规模新能源设备的装机，伴随着用户侧分布式储能、电动汽车等负荷接入，对台区运行稳定性提出了巨大挑战。如何进行台区可调控资源的协调控制以及不同类型能量单元的协调优化，已逐步成为研究热点。本工作遵循配电物联网体系架构，以台区领域应用需求为导向，开展以台区智能融合终端为基础的配电物联网用能管控系统建设。台区用能管控系统框架如图1所示。

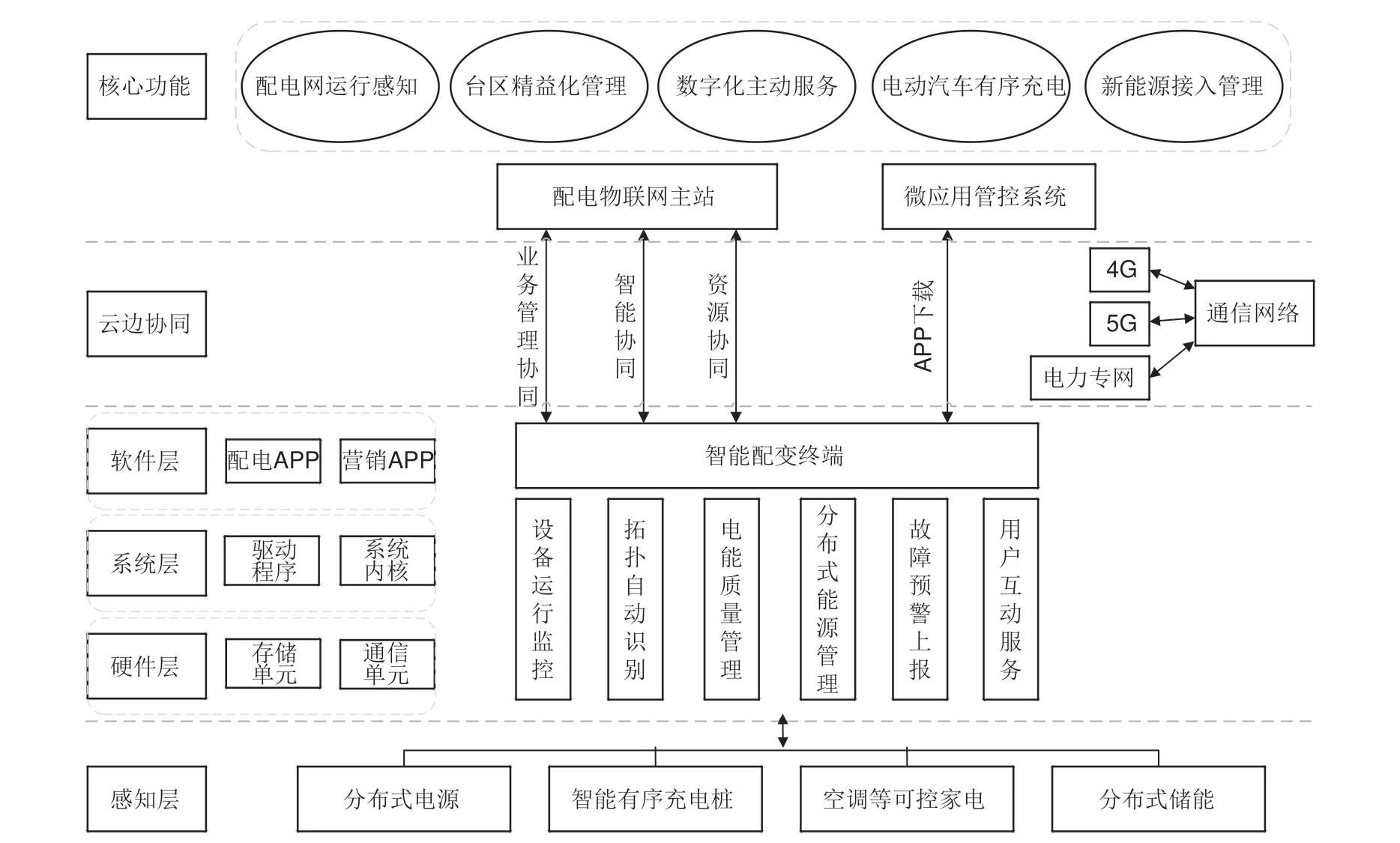
图1 配电台区用能管控系统框架Fig.1 Framework of energy control system in distribution transformer station area

在配电物联网“云、管、边、端”整体架构下，利用大数据技术、云边协同技术等构建台区用能管控系统框架。聚焦台区五大核心业务功能：对低压配网设备运行状态监测与控制；为台区线损、电价及治理提供数据支撑；利用智能感知单元与智能配变终端联合作用实现配电数字化转型；为分布式电源接入稳定运行提供保障；对电动汽车安全充放电进行管控。感知层负责收集用户分布式电源、电动汽车等负荷资源以及智能电表、故障诊断设备、开关设备等所采集的数据，通过智能配变终端进行识别与分析，并与云主站进行协同互动，利用微应用管控系统通过客户端APP 下载实现数据可视化，努力提升台区业务能力，做到“数据尽采集，状态尽感知，业务尽覆盖”。

2 配电台区用户侧可调控资源聚合模型

2.1 配电台区用户侧资源分类

台区用户侧可调控资源主要指柔性负荷，用户可根据需要灵活调节用能行为主动参与电网互动。用户侧柔性负荷可以按负荷运行特性和负荷用电时域特征分为两类[16]。

根据负荷运行特性的不同可分为可平移负荷、可转移负荷和可中断负荷。可平移负荷如洗碗机等无规定使用时间，但其运行受启停时间限制，一旦启动必须运行完成一个周期。可转移负荷如温控负荷等可灵活调整负荷曲线，但需保证一个周期内负荷总量不变。可中断负荷如照明用电等可由电网直接下达负荷削减指令，一般指对居民生活影响较小的家电。

根据负荷用电时域特征不同可分为工作日负荷和节假日负荷。一般来说，工作日为星期一至星期五，用户负荷普遍集中在早晚，白天负荷较小，而节假日负荷如周末等，用户负荷无明显集中时段，故工作日负荷和节假日负荷有明显差异。

为实现对台区不同类型用户可调控资源的用能管控，本文考虑负荷响应不确定性，将负荷可调控潜力及可靠性作为用户侧负荷分类原则之一，主要考虑温控负荷、电动汽车和用户侧分布式储能对台区用能管控的影响。

综上所述，台区用户侧资源分类如表1所示。

表1 台区用户侧资源分类Table 1 Classification of user-side resources

2.2 配电台区用户侧可调控资源聚合

大规模风电、光伏的开发利用，以及台区电动汽车充电桩、温控负荷、分布式储能等可调控资源的接入，给发电侧优化调度带来巨大挑战。分散式柔性负荷具有强随机性的特点且可调控性非常小，若配电台区对单个用户逐一管控，一方面增加了台区调度工作量，效率低下；另一方面会增加计算维度，可能无法计算出结果。故引入用户聚合商概念，对温控负荷、电动汽车和分布式储能进行有效聚合，以用户聚合商为代表参与台区用能管控。

2.2.1 温控负荷聚合模型

采用等效热参数建模方法建立单个温控负荷的模型，该方法将建筑物质热阻、空气热容等效为电路的电阻、电容元件，将光照、环境温度等效为电路的电源，利用该方法可基于单个温控负荷的热容、热阻建立功率与温度、时间和能效的关系[17]。由于不同温控负荷运行机理相同但等效热容C、等效热阻R和能效比η不同，在同一温度控制目标下，多个温控负荷出力模型可以等效为图2所示的等效热参数聚合模型。

图2 温控负荷等效聚合模型Fig.2 Equivalent aggregation model of temperature-controlled loads

由图2可得单个温控负荷的状态方程如下：

式中，C为等效热容；R为等效热阻；P(t)为t时刻内空调运行功率；Tout(t)和Tin(t)分别表示t时刻内室外和室内温度；η为空调能效比；u(t)为t时刻内空调运行状态。对式(1)进一步整理可得空调运行功率与室内温度变化的关系为：

式中，Δt为时间步长。

假设室温须保持在[Tmin,Tmax]范围内，且不考虑空调启停瞬间功率影响，根据能量守恒定律，空调制冷平均功率可等于热量散失平均速率，则单个温控负荷的平均功率为：

由于空调运行原理相同，对于台区更关心的是温控负荷群总用电功率，假设有N台空调，则温控负荷群总功率可根据单个温控负荷平均功率进行估算得出，即

考虑到t时刻平均室温可由t时刻空调平均设定温度代替，且N个空调的η和R相互独立，由图2可计算得出温控负荷聚合模型的等效η和R，则温控负荷群t时刻总用电功率为

其中，

式中，Req为聚合模型等效电阻；ηeq为聚合模型等效能效比；Tset.eq(t)为t时刻聚合模型空调等效设定温度；Tset.n(t)为t时刻第n台空调设定温度。

2.2.2 电动汽车聚合模型

电动汽车的充放电行为由用户主观意愿决定，一般来说，大部分车主会在相似的时间段在家庭或者工作地充电桩进行充电，若接入的电动汽车数目非常多，则很有可能在用电高峰对供电造成压力，故其对台区的有效调控提出了巨大的挑战。由于主要考虑台区用户用能管控，故仅考虑电动汽车作为负荷，不考虑其放电特性。

假设某辆电动汽车在时刻t0开始充电，起始荷电状态为SOC0，则t时刻电动汽车荷电状态为

式中，P为充电功率；η为充电效率；Q为电池容量。

取一天内24 h 为一个周期对电动汽车功率聚合，时间步长取1 min，将24 h 分为1440 个时间段，聚合后第i个时间段内充电功率为

式中，M为电动汽车数量；i取值1，2，3，…，1440；Pi,j为第j辆电动汽车在第i个时间段内的充电功率。

由于用户主观意愿的不同，每辆电动汽车的初始充电时刻、结束充电时刻、起始荷电状态和期望荷电状态都不同，为了对模型进行简化，本工作假设各电动汽车初始充电时刻和充电功率互相独立，各电动汽车充电结束时刻荷电状态到达最大值，各电动汽车充电功率恒定。采用蒙特卡罗场景模拟方法，首先对电动汽车数量初始化，然后通过随机抽取的初始充电时间和初始荷电状态计算充电时长，叠加电动汽车充电功率与时间的模拟曲线，直至叠加次数达到电动汽车数量上限，最后绘出电动汽车充电功率聚合曲线，具体流程如图3所示。

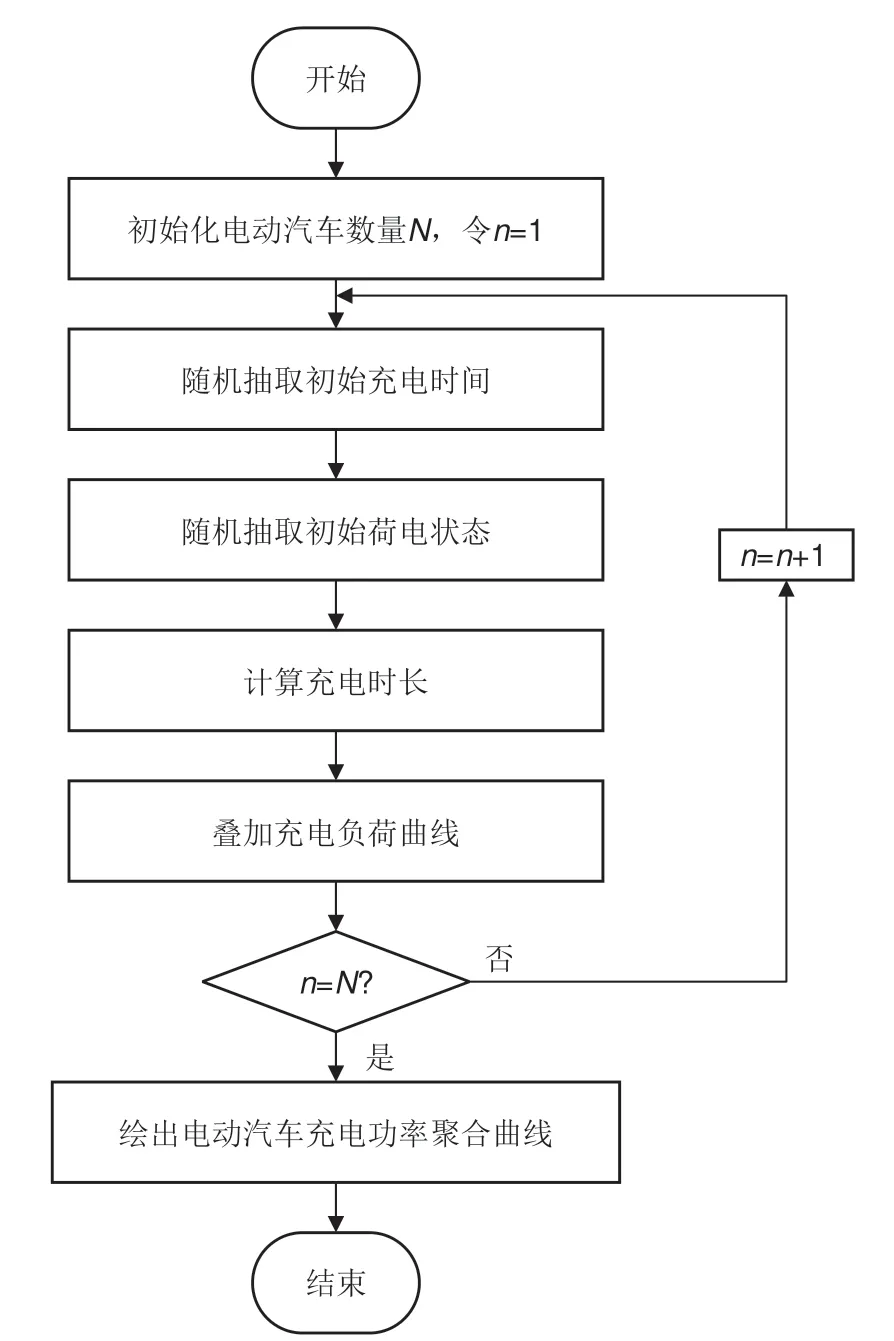
图3 电动汽车充电功率聚合流程Fig.3 Electric vehicle charging power aggregation process

2.2.3 分布式储能聚合模型

用户侧分布式储能的引入可以满足用户灵活调整用能负荷需求，但用户侧分布式储能具有数量多且分散的特点，台区无法有效管控，故需对其进行聚合管理，分布式储能聚合模型如下：

式中，D为分布式储能数量；Pchar(t)和Pdis(t)分别为t时刻内分布式储能充放电聚合功率；Pchar.d(t)和Pdis.d(t)分别为t时刻内第d台分布式储能充放电功率；ηchar.d和ηdis.d分别为第d台分布式储能充放电效率；E(t)为t时刻内分布式储能聚合能量；Uchar.d(t)和Udis.d(t)分别为t时刻内第d台分布式储能的充放电运行状态变量，其值为1表示运行，反之表示停止，为避免第d台分布式储能在同一时刻同时充放电，需满足

实际运行时，各分布式储能需满足充放电约束和容量约束，即

式中，T为24 h；Pchar.d.max和Pdis.d.max分别为第d台分布式储能最大充放电功率；Ed.max为第d台分布式储能最大容量；ζ为循环充放电限制次数。

3 配电台区用户可调控资源协调调度策略

为了实现台区对不同类型用户可调控资源的用能管控，以提高台区运行稳定性及新能源消纳比例，这里提出一种计及用户用能成本和用能舒适度的基于分时电价和储能充放电策略的台区用户可调控资源协调调度方法。考虑到台区用户个体数量大、分散广的特点，将台区若干个用户聚合为用户聚合商，其可调控资源用能功率由第2节所述，风电、光伏出力及不可调控负荷由日前预测值表示，用户聚合商可与电网交互电能，以最小化用户用能成本及最大化用能舒适度来提高用户侧参与台区调控的主观能动性。

3.1 目标函数

3.1.1 用户聚合商用电成本

用户聚合商用电成本为向电网售电收益与购电成本之差，表达式如下：

式中，CP为用户聚合商用电成本；Pbuy(t)和Psell(t)分别为t时刻内用户聚合商需要购买和售出的电功率，其值为新能源出力、储能充放电功率与用电负荷之差，当新能源出力与储能放电功率不满足负荷需求时需要向电网购买电能，当新能源出力满足储能充电和负荷需求且有余量时，向电网出售电能；cfs(t)和csw(t)分别为t时刻内电网分时电价和上网电价。

3.1.2 用户聚合商用能舒适度

用户聚合商用能舒适度主要考虑对温控负荷即空调的使用舒适度，尽可能满足用户对室温的设定要求。温度舒适度的评判标准与室温和最适温度上下限有关，在用户设定温度的范围内，室温与最适温度偏差百分比越大，用户用能舒适度越低，表达式如下[18]：

式中，Ω(t)为t时刻内室温偏离最适温度百分比；Tin(t)为室内温度；Tfit.max和Tfit.min分别为最适温度上下限，文中取27 ℃和23 ℃；k(t)为空调运行状态变量，其值为1，表示空调运行，反之表示空调停止；F为用能舒适度指标。

综上所述，用户聚合商目标函数为

式中，λ1和λ2为线性加权权重。

3.2 供电可靠性约束

考虑到配电台区用户的供、用电平衡是节省用户用电成本及提高用能舒适度的重要前提，系统应满足各时段负荷功率、新能源出力、储能装置充放电功率及用户聚合商与电网交互功率平衡约束，可表示为

式中，Pload.fix(t)为t时刻内不可调控负荷功率；Pload.con(t)为t时刻内可调控负荷功率，即温控负荷、电动汽车及分布式储能充电功率；Pp.w(t)为t时刻内新能源出力；Pgrid(t)为t时刻内用户聚合商与电网交互功率，当新能源出力与储能放电功率不满足负荷需求时，其为正值，反之为负值；Pdis(t)为t时刻内分布式储能放电功率，其满足分布式储能不同时充放电约束。

3.3 协调调度策略

考虑到电价对用户用电行为的影响以及对分布式储能充放操作的调节作用，同时为提高台区可调控资源多目标优化调度模型的有效性以及分布式储能运行的安全性，本文提出两点协调调度策略。

（1）用户侧分布式储能的充放电应基于电网分时电价的影响，即在电价谷值时对储能进行充电，在电价峰值时利用储能进行放电，以减少用户侧用电成本。

（2）用户侧分布式储能充放电应避免越限情况发生，即当t- 1时刻储能SOC已达最大值，则t时刻不再进行充电操作，当t- 1 时刻储能SOC 已达最小值，则t时刻不再进行放电操作。

基于上述策略，有如下具体实施方案。

（1）当新能源出力满足负荷需求时，优先给储能充电，当储能SOC 上限时，若有余量则出售给电网获利。

（2）当新能源出力不能满足负荷需求时，分为以下3 种情况：当分时电价处于谷值时，用户侧从电网购电补齐负荷差额，同时购电为储能充电直至SOC上限；当分时电价处于平值时，用户侧从电网购电补齐负荷差额，储能不动作；当分时电价处于峰值时，优先利用储能放电来满足负荷需求，当SOC 到达最小值且仍供不应求时，再从电网处购电。

3.4 求解算法

台区可调控资源调度模型需要历史气象数据和用电数据预测下一日风电、光伏出力及不可调控资源用能功率，需要根据可行解的各边界条件来生成目标函数最优解。因此，本工作采用差分进化算法对模型进行求解，利用其收敛速度快、控制参数少来提高模型求解精度，提高非劣解的多样性，通过变异、交叉、选择三个过程来寻最优解，具体求解流程如图4。

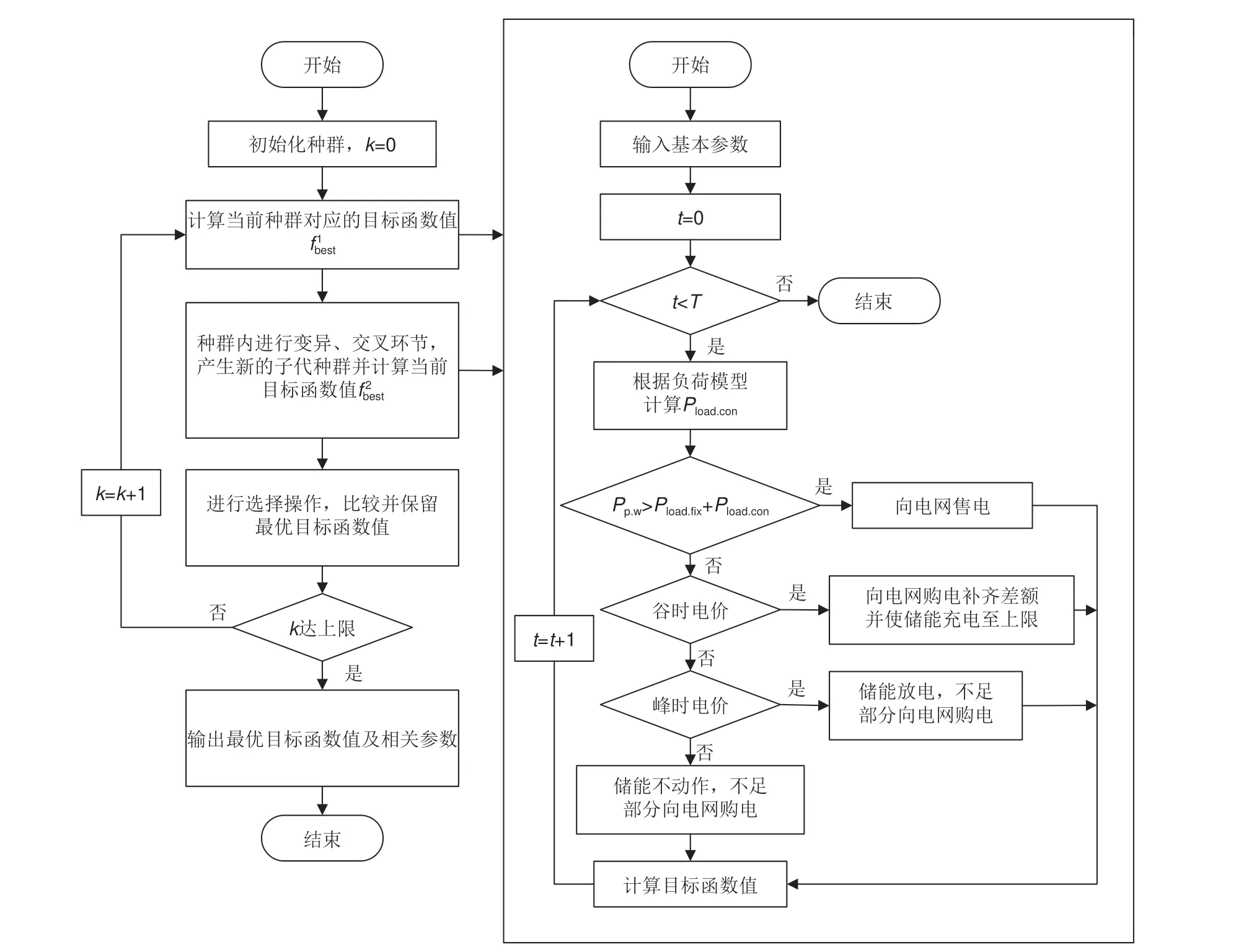
图4 算法求解流程Fig.4 Solving process

4 算例分析

算例分析分为两部分，第一部分为验证台区可调控资源聚合模型的有效性，第二部分为验证所提计及用户用电成本及用能舒适度的基于分时电价和分布式储能充放电策略的台区可调控资源协调调度策略的有效性。

4.1 台区可调控资源聚合模型有效性分析

4.1.1 电动汽车聚合模型有效性分析

选择台区用户电动私家车进行仿真分析，设定台区用户电动私家车有三个充电场景：早晨上班后在公司充电；中午外出在商场充电；晚上下班后在小区充电。假设台区用户电动私家车充电次数分为三种类型：每天充一次电；每天充两次电；每天充三次电。三种类型用户所占比例分别为6∶3∶1。每天充一次电的用户选择在下班后利用小区停车位充电桩进行充电，直至充满。每天充两次电的用户选择在上班后和下班后充电。每天充三次电的用户选择在三个场景均进行充电。设定电动汽车起始荷电状态满足正态分布N(0.6，0.1)，早上充电的电动汽车起始充电时间满足正态分布N(540，60)，中午充电的电动汽车起始充电时间满足正态分布N(840，120)，晚上充电的电动汽车起始充电时间满足正态分布N(1440，120)[17]。设定电动汽车容量为30 kW，充电效率为0.9，场景1和2电动汽车充电功率为24 kWh，场景3电动汽车充电功率为7 kWh。利用蒙特卡罗算法进行场景模拟，对1000 辆电动私家车进行功率聚合，结果如图5所示。

由图5(b)可知电动汽车聚合功率在9：00 与20：00出现两次峰值，充电时间主要集中在8：00—10：00和18：00—21：00，与此同时，用户负荷在这两段时间内也处于高负荷状态，此时电动汽车接入充电桩必然会增加台区供电压力。由于电动汽车充电时间稍作调整并不会对用户生产生活造成太大影响，所以基于电动汽车聚合模型，加上合理的调度策略，将电动汽车充电时间转移，可以很大程度提高台区对负荷调控的能力，增加台区运行稳定性。

图5 电动汽车充电功率聚合Fig.5 Electric vehicle charging power aggregation

4.1.2 温控负荷聚合模型有效性分析

由于空调负荷在夏季和冬季使用较多，且空调制冷和制热运行原理及功率聚合分析类似，故本工作选取夏季典型日对1000 台空调进行负荷聚合分析。某示范台区用户空调负荷参数区间为R∈[1.5, 2.5],C∈[1.5, 2.5],η∈[2.6, 3]，假 设1000 台空调负荷参数在区间内服从随机分布，不考虑空调启停瞬时功率的影响，可由式(5)～式(8)计算得出空调负荷聚合功率。假设空调温度在区间[24, 26]内，不同温度下空调负荷聚合功率如表2所示。

表2 不同温度下空调负荷聚合功率Table 2 Aggregate power of air conditioning load at different temperatures

由表2可知，空调负荷聚合功率在相同设定温度下随着室温的升高而增加，这是由于室内外温差大，当室外温度相对较高时，空调会增加制冷量来维持室内设定温度，从而增加了负荷功率，这与实际空调作用情况基本保持一致，聚合后的空调负荷模型可作为重要的可调控资源参与台区互动，提升台区的用能管控能力。

4.1.3 分布式储能聚合模型有效性分析

对1000 台分布式储能进行功率聚合分析，假设分布式储能含两组铅酸电池，储能电池容量为49.6 kWh，充电时长约8 h，单组电池平均充电功率为3.1 kW。考虑到用户为节约用电成本，更愿意在电价谷时24：00—8：00 对储能电池进行充电，设定分布式储能电池充电起始时间服从正态分布N(1440，120)，起始荷电状态服从正态分布N(0.5，0.1)[17]，可得1000 台分布式储能充电聚合功率如图6所示。

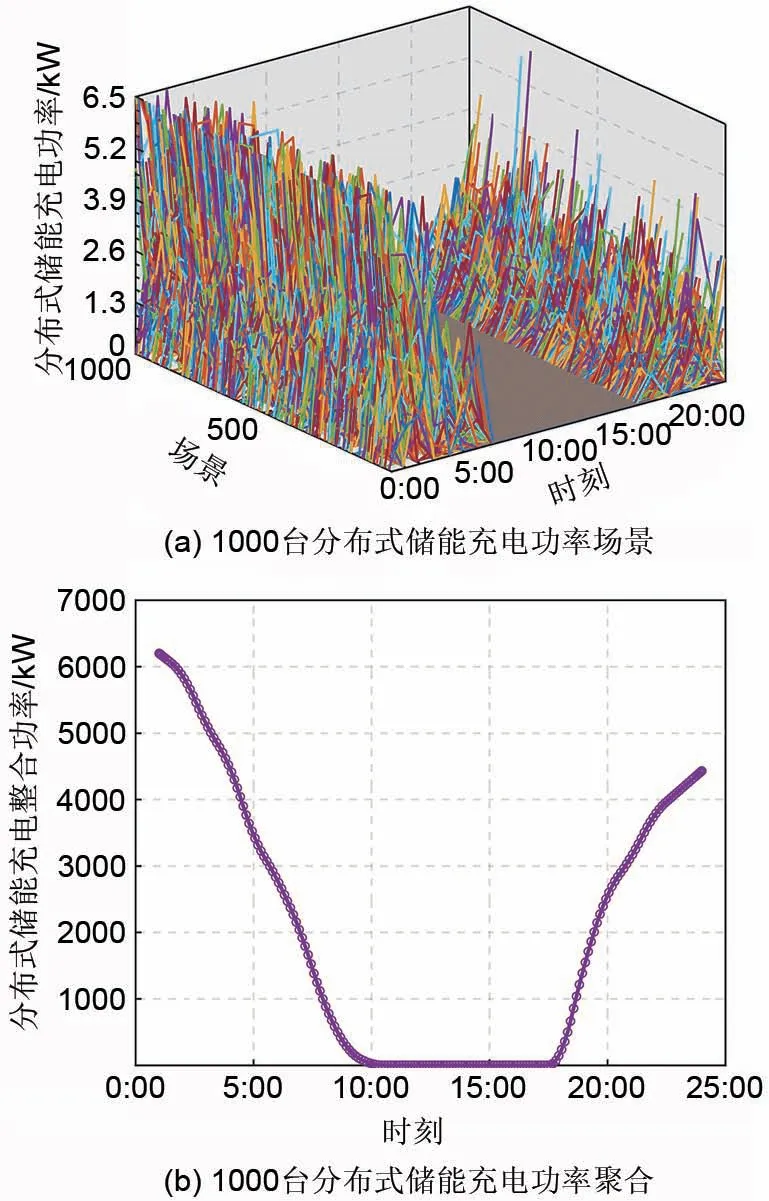
图6 分布式储能充电功率聚合Fig.6 The charging power aggregation of distributed energy storage

由图6(b)可知，用户分布式储能聚合模型在24：00—8：00 充电，在10：00—18：00 放电，在19：00—23：00 继续充电。在凌晨负荷较小且电价较低时充电，在午时高负荷状态下放电符合用户减少用电成本需求，但是在未调控情况下，储能电池在晚间用能高峰期且电价峰值时又继续充电，会增加用户用电成本且提升台区供电压力，故需有效控制分布式储能充放电时段以满足台区对可调控资源的协调调度。

4.2 协调调度策略有效性分析

4.2.1 基本数据

以某示范低压配电台区为例，选择夏季某典型日进行仿真分析，将1000 个用户聚合为负荷聚合商参与台区互动。假设用户侧分布式电源有平均额定容量为6 kW的风力机组和4 kW的光伏机组，负荷聚合商不可调控负荷及分布式电源各时段预测出力如图7所示。设定电网峰、平、谷时价(单位为元/kWh)分别为1.25，0.8，0.4；上网电价(单位为元/kWh)为0.35；使用差分进化算法种群数量设置为35，最大迭代次数设置为100，偏差放大系数设置为0.5，交叉因子设置为0.9。

图7 不可调控负荷功率及风电、光伏出力Fig.7 The power of uncontrollable loads, wind power and photovoltaic

4.2.2 仿真结果分析

基于分时电价与分布式储能充放电策略的负荷聚合商电动汽车充电功率和分布式储能充电功率如图8 所示。系统调度结果如图9 所示。对比图8 与图5，明显看出图5中9：00与20：00的充电功率峰值在图8 中均有所减小且图8 中晚间电动汽车充电功率峰值时段推移到了23：00，这是由于考虑分时电价的影响，用户聚合商为减少用电成本，主观上更愿意在电价谷时对电动汽车充电，此改变并不会对用户生活造成很大影响，同时又能替用户节省成本，而对台区而言，用户侧电动汽车充电时段避开了负荷高峰期，在一定程度上可降低台区供电压力，提高台区运行稳定性。分析图8中分布式储能充电功率的变化可知，在分时电价谷值时，即24：00—8：00 储能进行充电操作；同时对照图9可知，在分时电价平值时，即8：00—10：00，16：00—18：00 和22：00 储能无操作，尽管在10：00，18：00 和22：00 系统处于供不应求状态，用户仍选择以相对较低的价格向电网购电；在分时电价峰值时，即11：00—15：00 期间，新能源出力不能满足负荷要求，用户优先利用分布式储能放电来补齐用电差额，节省了电价峰值时的购电成本，而在19：00—21：00 期间，分布式储能放电已至上限，只能通过向电网购电来满足用电需求。在8：00、9：00和16：00期间，新能源出力满足用电需求外仍有剩余，且分布式储能无需执行充电操作，故用户可将多余电量出售给电网而获利，以补贴用电成本。

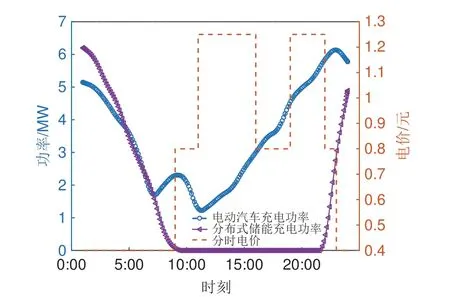
图8 优化后电动汽车与分布式储能充电聚合功率Fig.8 Optimized charging power aggregation of EV and distributed energy storage

图9 调度结果Fig.9 The scheduling results

室温控制结果如图10 所示。出于对用户使用空调的习惯考虑，假定7：00—9：00和16：00—18：00 空调为关闭状态，24：00—6：00 为恒温状态。优化前由于未考虑用户用电成本及用能舒适度的影响，用户在10：00和19：00启动空调时为了迅速制冷会将空调温度设定较低，而当室外温度与室内设定温度相差较大时，空调需要迅速提供较多的制冷量从而需要消耗更多电能，当室温稳定时，室内外温差偏大将降低用户用能舒适度。优化后的室温曲线明显减少了峰谷差，在满足用户对制冷需求的同时可以减少空调用电功率，在负荷高峰期降低台区供电压力。

图10 优化控制前后室内温度变化Fig.10 The change of indoor temperature through controlling

优化前后用户聚合商用电成本及用能舒适度对比如表3所示。由表可知，优化后用户购电成本比优化前减少了3080.5元，售电收益增加了722.6元，用能舒适度由原来的0.75变为0.647，温度偏差百分比减小表明用户温度感觉灵敏度降低，温度舒适度提高。

表3 优化控制前后经济性与舒适度指标对比Table 3 Comparison of economy and comfort index through controlling

5 结论

为实现配电台区对用户不同类型可调控资源的用能管控，本文遵循配电物联网体系构建了新型电力系统下配电台区用能管控系统框架，针对负荷响应不确定性对台区可调控负荷进行分类并研究其聚合模型，提出了一种基于分时电价与分布式储能充放电规则的协调调度方法，通过算例分析得出如下结论：

（1）通过协调调度策略使得电动汽车9：00充电聚合功率峰值减小，晚高峰由20：00 转移至23：00，分布式储能基于充放电规则实现在电价谷时充电，电价峰时放电，充电时段避开负荷高峰期，缓解了配电台区供电压力。

（2）用户购电成本减少了3080.5 元，售电收益增加了722.6 元，温度偏差由原来的0.75 变为0.647，有效降低了用户用电成本，提高了用户使用空调的舒适度，调动了用户参与配电台区负荷调控的积极性，有利于配电台区的有效用能管控。

（3）基于配电物联网技术，配电台区用能管控系统架构配合协调调度策略可支持台区快速落地各种应用需求，实现本地控制与云端协同，为智能配电台区数字一体化发展提供了思路。