融合自适应惯性权重和柯西变异的秃鹰搜索算法

丁 容,高建瓴,张 倩

(贵州大学 大数据与信息工程学院,贵阳 550025)

1 引 言

近年来,随着自然科学的发展,传统的计算方法在复杂的约束条件下求解出最佳方案时所碰到的问题已变得越来越突出,存在求解精度低、成本高、耗时较长等方面的缺陷.针对传统计算方法求解复杂问题的局限性,为了求解复杂的优化问题,在巨大的搜索空间内寻找最优解,许多学者设计了群智能优化算法,例如粒子群算法[1]、蚁群算法[2]、花授粉算法[3]、细菌觅食优化算法[4]、磷虾群算法[5]等.群智能优化算法主要对自然界生物的群体行为进行模拟.个体的进化或觅食过程被模拟为搜索和优化的过程,以搜索空间的点作为归因,去模拟自然界中的个体,将求解问题的目标函数衡量为个体对环境的适应能力,个体适者生存这个过程或者觅食过程就好比在搜索和优化过程中不断迭代的过程,即用更好的可行解替换之前的可行解.

秃鹰搜索优化算法(Bald Eagle Search,BES)[6]是2020年马来西亚学者Alsatter提出的一种新型元启发式算法,它模仿秃鹰在寻找鱼类时的狩猎策略或智能社会行为.该算法具有较强的全局搜索能力,在应对各类复杂数值优化问题时都能够有效的解决,但是,BES算法存在参数较多,收敛速度较慢,以及精度不高等缺陷,且在算法迭代过程中容易陷入局部极值.

群智能优化算法都存在收敛速度慢且易陷入局部最优的缺陷,为了提高算法的寻优能力,众多学者都提出了改进的方法:刘明霞等[7]将混沌映射算子应用到蚁群算法中,增强了种群的多样性,且在一定程度上避免了算法陷入局部最优.Oliva等[8]在鲸鱼位置更新概率中引入混沌映射算子,提高了鲸鱼算法的全局寻优能力.杨万里等[9]提出了基于 Logistic映射的新型混沌简化 PSO算法,保留了种群的多样性,降低了算法困于局部最优的概率.Teng等[10]提出了将Tent映射初始化GWO种群,避免了种群的随机性带来的缺陷,提高了GWO算法的收敛性.Hegazy等[11]在算法中引入自适应权重因子,提高了算法的收敛速度.Wang 等[12]在速度的更新方式中提出自适应惯性权重,在搜索过程中蝙蝠可以动态调节相关速度.王依柔等[13]在园丁鸟的位置更新方式中通过引入正弦的惯性权重因子,能够有助于算法保持较好的搜索能力.Wang 等[14]通过引入柯西变异算子,降低了萤火虫算法陷入局部最优的概率,而且全局搜索能力得到了提高.Taher等[15]通过引入变异更新,提出了混合策略蝗虫优化算法,增大了蝗虫的搜索空间以及避免陷入局部最优值.Li等[16]提出了将柯西变异融入到粒子群优化算法,在精度和收敛速度和时间复杂度上都得到了改善.Xu 等[17]将高斯变异和柯西变异结合,能有效地提高MFO算法的搜索能力.

文章的主要研究工作:提出了融合自适应惯性权重和柯西变异的秃鹰搜索算法(CBES),该算法首先使用 Tent 混沌映射初始化种群,使得种群的初始个体在搜索空间内更加的均分分布,将求解效率与精度提高,保留了种群的多样性;其次,将自适应惯性权重和柯西变异融入秃鹰搜索优化算法,改善局部搜索与全局收敛能力,提升了算法的寻优性能.通过12个基准测试函数将CBES和其他4种算法进行测试对比,实验结果表明该算法具有更好的寻优能力和鲁棒性,同时将算法引入实际工程领域,验证了该算法的实用性和拓展性.

2 秃鹰搜索优化算法

秃鹰遍布于北美洲地区,秃鹰主要选择鱼类作为主要食物.以捕食鲑鱼为例,秃鹰首先找到搜索空间是通过自我搜索或者跟踪其他鸟类到鱼的浓度;当它们在水点上寻找食物时,秃鹰会朝特定方向出发,选择某个区域开始搜索;由于秃鹰的视力极佳,能够从很远看到猎物,一旦发现猎物,秃鹰会随着运动的逐渐流动而下降,以高速冲向猎物并从水中抢夺鱼.秃鹰搜索算法模拟秃鹰在狩猎过程中的行为,秃鹰狩猎分为3个阶段.在第1阶段,秃鹰选择猎物数目最多的空间;在第2阶段,秃鹰在选定的空间内移动以寻找猎物;在第3阶段,秃鹰从第2阶段确定的最佳位置摆动,并确定最佳狩猎点.

2.1 选择搜索空间

在选择阶段,秃鹰选择并确定搜索空间中的最佳区域用于寻找猎物.秃鹰的位置Pi,new更新方式是通过随机搜索过程中的先验信息与α相乘来确定的,式(1)从数学上描述了这种行为.

Pi,new=Pbest+α×r(Pmean-Pi)

(1)

其中,α表示控制位置变化的参数,取值在1.5～2之间;r是一个随机数,取值在0～1之间;Pbest表示秃鹰目前根据其先前的搜索中确定的最佳搜索位置;Pmean表示秃鹰在经过前次搜索后所在的平均分布位置;Pi是指第i只秃鹰所在的位置.

2.2 搜索空间猎物(探索)

在搜索阶段,秃鹰从上一阶段确定的搜索空间中寻找猎物,并在螺旋空间内朝不同的方向移动,以加速搜索.螺旋飞行的数学模型使用极坐标方程进行位置更新,如下所示:

θ(i)=a×π×rand

(2)

r(i)=θ(i)+R×rand

(3)

xr(i)=r(i)×sin(θ(i))

(4)

yr(i)=r(i)×cos(θ(i))

(5)

(6)

(7)

其中,θ(i)与r(i)分别表示螺旋方程的极角与极径;a是值在(0,5)区间内的一个参数,用于确定中心点中的点搜索之间的角;而R取值在0.5～2之间,用于确定搜索周期的数目;x(i)与y(i)表示在极坐标下秃鹰的位置,取值均为(-1,1);秃鹰在选定的搜索空间内向螺旋方向移动并确定俯冲和捕获猎物的最佳位置.秃鹰位置更新如下所示:

Pi,new=Pi+x(i)×(Pi-Pmean)+y(i)×(Pi-Pi+1)

(8)

式(8)中,Pi+1表示第i只秃鹰下一更新的位置.

2.3 俯冲捕获猎物(利用)

在俯冲阶段,秃鹰以搜索空间的最佳位置作为出发点,向目标猎物快速摆动,种群中其他个体也紧随着向最佳点方向移动并对猎物展开攻击,利用极坐标方式来描述运动状态,如下所示:

θ(i)=a×π×rand

(9)

r(i)=θ(i)+R×rand

(10)

xr(i)=r(i)×sin(θ(i))

(11)

yr(i)=r(i)×cos(θ(i))

(12)

(13)

(14)

秃鹰的位置更新方式如下所示:

(15)

Pi,new=rand×Pbest+δx+δy

(16)

在式(15)中,c1,c2∈[1,2],参数c1和c2会增加秃鹰向最佳中心点移动的强度.

3 秃鹰搜索算法的改进

相较于其他智能优化算法,秃鹰搜索算法在收敛速度和精度性能上略胜一筹,但算法本身仍存在容易陷入局部最优和收敛精度低的问题.因此本文提出了一种改进的秃鹰搜索算法(CBES).主要从3个方面对原始的秃鹰搜索算法进行改进,首先,使用Tent混沌映射对种群进行初始化,有效保持种群的多样性,提高秃鹰的全局搜索能力;其次在搜索阶段通过融入自适应惯性权重来提高秃鹰的局部搜索能力;最后使用柯西变异提升算法的整体寻优能力.

3.1 Tent 混沌映射

在解决函数优化的过程中,BES算法通常使用随机产生的数据作为初始种群信息,使得种群的多样性遗失,算法的寻优结果也会相应的变差.然而,混沌作为自然界普遍存在的一种非线性现象,因为混沌变量的特性包含随机性、遍历性和规律性[18],很多学者根据这些特点将其应用于算法优化问题,既能保持种群的多样性,又能帮助算法跳出局部最优,改善算法的全局搜索能力.目前常用的混沌模型有Tent映射、 Logistic 映射、Sin映射等,但是,不同的混沌模型对算法寻优能力有不同的影响.单梁等[19]研究验证了在均匀分布和收敛速度方面Tent 映射均优于 Logistic 映射,通过严格的数学推理,在[0,1]区间内Tent映射可以产生优化算法的混沌序列.

文章使用Tent映射来初始化种群,Tent映射的表达式如下所示:

(17)

即经过贝努利移位变换后表达式如下:

xi+1=(2xi)mod1

(18)

Tent混沌映射初始化种群产生序列的具体步骤如下:

Step 1.在区间(0,1)内随机产生初始值x0,记作i=0;

Step 2.根据式(17)进行迭代运算产生一个新的x序列,且i=i+1;

Step 3.当i达到最大迭代次数时,则停止迭代,且将迭代产生的x序列保存下来.

3.2 自适应惯性权重

惯性权重因子w是算法中比较重要的一个参数,Shi[20]于1998年首次提出将惯性权重因子w引入PSO算法,来达到收敛速度和局部寻优能力之间的平衡,取得了较为良好的效果.随后的许多研究也验证了引入惯性权重因子能够有效平衡算法的全局搜索和局部搜索.

当惯性权重较大时,算法的全局搜索能力较强,可以提高种群多样性,可以搜索较大的区域;惯性权重较小时,算法具有较强的局部搜索能力,可以围绕最优解进行精细搜索,加快收敛速度.在搜索空间猎物阶段,秃鹰需要在选定的搜索空间内寻找猎物,为了使秃鹰的局部寻优能力得到提高且在迭代中取得最优的适应度值,本文提出了新的自适应权重的方法,自适应惯性权重公式如下:

(19)

其中,t表示当前迭代数;tmax是设置的种群最大迭代次数;wmax是初始惯性权重,在文中取值为0.92;wmin是秃鹰种群最大迭代次数时的惯性权重,在文中取值为0.4.将惯性权重因子引入秃鹰搜索优化算法中,在探索阶段,秃鹰的位置更新的表达式如下:

Pi,new=w×Pi+x(i)×(w×Pi-Pmean)+
y(i)×(w×Pi-Pi+1)

(20)

3.3 柯西变异

针对秃鹰算法易陷入局部极值的缺点,本文在原有的算法中融入柯西变异算子,改善算法的全局搜索能力,扩大搜索空间.柯西分布是一种在概率论中常见的连续型概率分布,柯西分布在原点处的概率密度较大,两端处的密度较小;两端的形状又长又扁.正因此特点可以通过融入柯西变异对秃鹰个体产生较大的扰动,使得算法更容易跳出局部最优值[21].标准的柯西分布概率密度函数公式如下:

(21)

柯西分布从峰值下降至两侧时相对平缓,且峰值相对较小,在变异后秃鹰种群会在搜索相邻空间时使用较少的时间,将主要精力花费在寻找全局最优值上.使用式(22)对搜索空间猎物阶段获得的全局最优值进行变异处理:

Pnew,best=Pbest+Pbest×Cauchy(0,1)

(22)

4 CBES算法描述

基于3.1节～3.3节对BES算法的改进,CBES算法具体实现流程如下所示:

Step 1.设置并初始化算法参数,其中包含种群的规模N,最大迭代次数tmax,目标函数的维度以及初始值的边界条件.

Step 2.使用2.1节中的Tent混沌映射对种群进行初始化,按照适应度函数求出每只秃鹰的适应度值,对所有秃鹰的适应度值排序,找出当前种群的全局最优位置.

Step 3.在秃鹰选择搜索阶段,按照公式(1)进行位置跟新.

Step 4.在秃鹰搜索空间猎物阶段,按照公式(20)进行位置更新.

Step 5.在俯冲阶段,按照公式(22)对上一个步骤得到的全局最优解进行柯西变异处理,再将得到的结果按照公式(16)进行秃鹰的位置更新.

Step 6.更新秃鹰种群的最优个体位置与适应度值,更新算法的迭代次数.判断算法是否满足设置的最大迭代次数或者精度要求,若满足,则终止算法,输出适应度最优值及最优解;若没有,则返回Step 3进行循环.

5 仿真实验与结果分析

5.1 实验参数设置

实验环境为:CPU为i5-4288U 2,运行内存为4G,操作系统为windows10,算法的运行环境为MATLAB2016a.设置5个算法的种群规模N均为30,迭代的最大次数为1000,每种算法独立运行30 次.

5.2 测试函数

为了验证改进的BES在收敛性以及精度性能上相比原始秃鹰算法更优,本文选取了12个测试函数进行实验对比,其中包括连续单峰函数和复杂非线性多峰函数,详细的测试函数信息见表1.

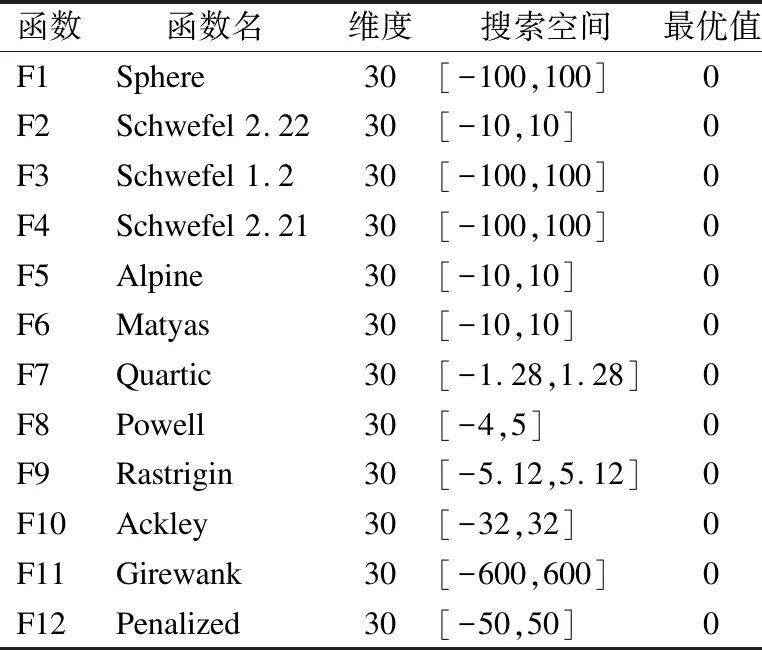
表1 标准测试函数Table1 Standard test functions

5.3 结果分析

为了验证本文改进后CBES的收敛性以及稳定性,选取秃鹰搜索算法(BES)、花授粉算法(FPA)、粒子群算法(PSO)、飞蛾火焰优化算法(MFO)进行对比实验.为了降低随机性给实验带来的影响,本文选取5种算法分别在12个测试函数上独立运次30次.表2分别列出了CBES、BES、MFO、PSO、FPA算法独立运行30次所得的最优值、最差值、平均值、标准差.

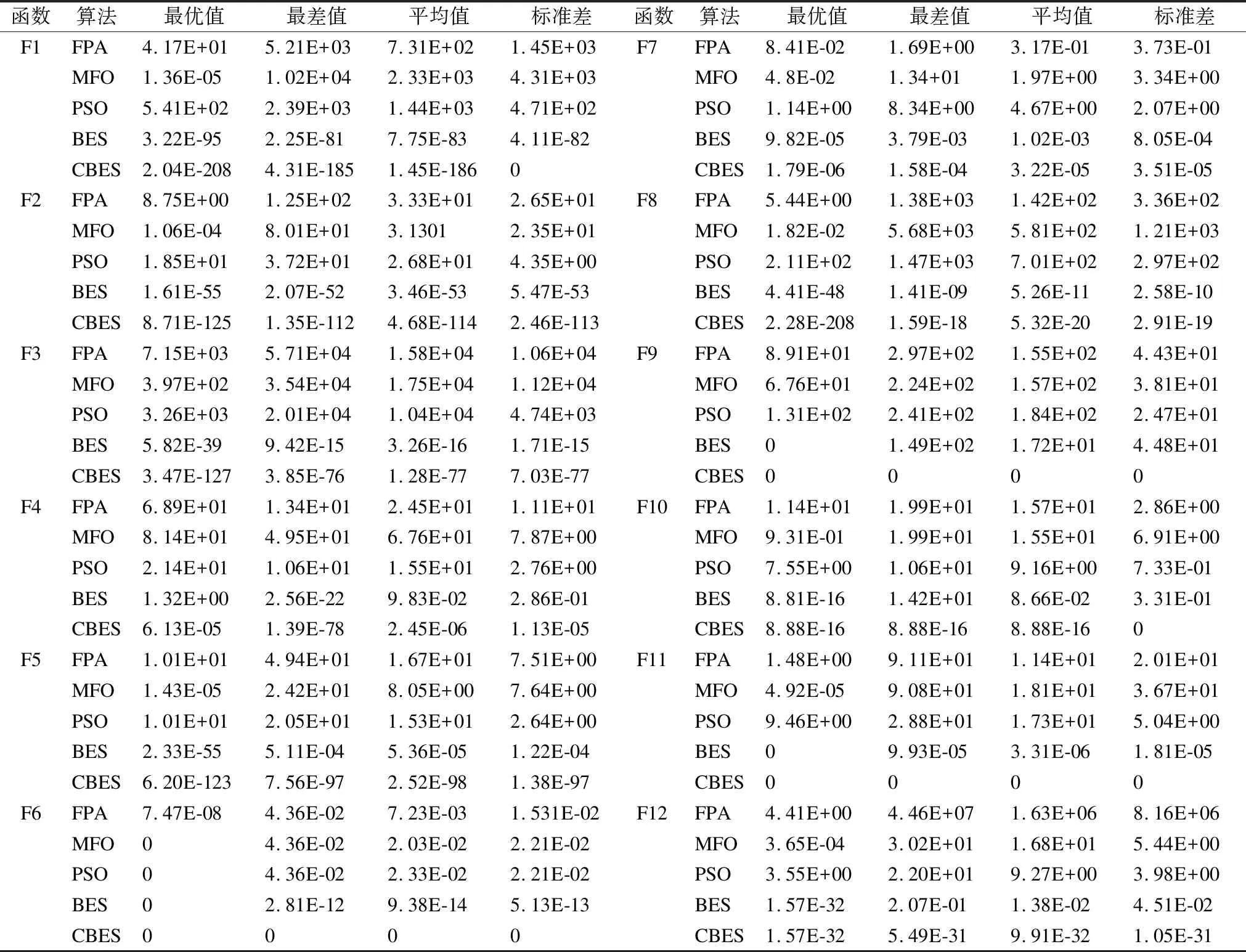
表2 测试函数的实验结果Table2 Experimental results of the test functions

根据实验结果可以得知,在所有的测试函数寻优过程中,本文提出的融合自适应惯性权重和柯西变异的秃鹰搜索算法全部优于BES、FPA、MFO、PSO.

算法的鲁棒性体现在标准差方面,当标准差数值越小时,算法的鲁棒性越好;相反,标准差数值越大时,算法的鲁棒性越差.由表2可知,在函数F1、F6、F9、F10、F11寻优过程中,CBES所得的标准差为0,表现出了较好的鲁棒性.对于函数F2、F3、F4、F5、F7、F8、F12,CBES算法所得的标准差均明显小于BES、FPA、MFO、PSO,CBES算法具有更高的收敛精度.

表2中算法所得的最优值和最差值反映了算法寻优结果的质量.从表2 可以看出:在基准测试函数F6、F9、F11中,CBES寻到理论上最优值0;在F1、F2、F3、F5、F8寻优过程中,CBES虽然没有寻到理论最优值,但在数量级上明显优于其他4种算法,与基本BES相比,具有更好的寻优能力.对于函数F10、F12,虽然CBES与BES获得的最优值相同,但是最差值对比的话,显然CBES在寻优能力上优于BES.对于函数F4、F7,与其他4种相比,CBES也能够得到更好的寻优结果.

算法所得的平均值反映了算法的稳定性,从表2数据可知,CBES在12个基准测试函数中所得的平均值均小于其他4种算法,所以CBES具有更高的收敛精度且寻优结果稳定.

综上所述,CBES在精度、收敛速度、稳定度方面都有所提高,总体鲁棒性也优于其他4种算法.为了能够更加直观地对比CBES与其他4种算法的优化效果,本文选取了12个基准测试函数的寻优进化曲线,如图1所示.

6 实际工程应用

为了进一步将本文提出的CBES算法应用到具体的实际工程领域,本文选取压力容器设计问题来验证算法在工程应用中的可行性.

压力容器设计问题属于典型的约束优化问题,其主要目的是使得压力容器在制作方面的成本能够达到最小,压力容器的模型如图2所示.压力容器的两端都有盖子封顶,头部一端的封盖为半球状.L是指在不考虑头部的情况下圆柱体的截面积长度,R则表示圆柱体的内壁半径,Ts和Th分别表示圆柱体部分壁厚和头部的壁厚.Ts、Th、R、L是压力容器设计问题的4个优化变量,为方便起见,将其表示为x1、x2、x3、x4.问题的目标函数和4个优化约束表示如下:

Minf(x)=0.6224x1x2x3x4+1.7781x2x32+

3.1661x12x4+19.84x12x3

(23)

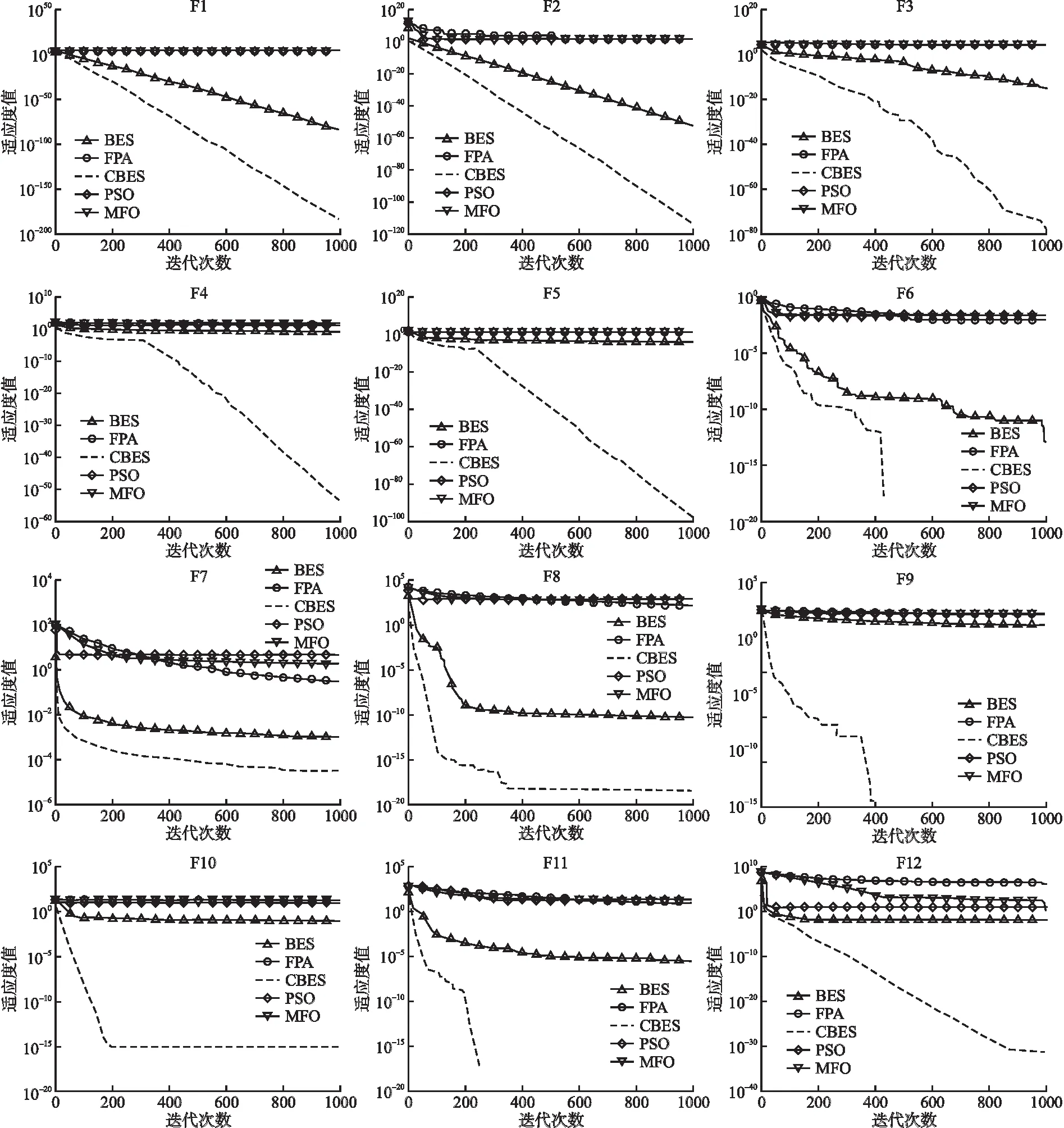
图1 不同算法的收敛曲线对比Fig.1 Convergence curve comparison of different algorithms

约束条件为:

g1(x)=-x1+0.0193x3≤0

(24)

g2(x)=-x2+0.00954x3≤0

(25)

g3(x)=-πx32-4πx33/3+1296000≤0

(26)

g4(x)=x4-240≤0

(27)

其中0.0625≤x1≤6.1875,0.0625≤x2≤6.1875,10≤x3≤200,10≤x4≤≤200.

对于处理约束优化问题重要的一个步骤是如何处理设置约束条件,本文使用罚函数法来建立约束条件和目标函数.将CBES算法以及PSO、MFO、FPA、BES进行求解结果对比,其对比实验结果如表3所示.从表3可以得知,CBES算法在求解压力容器设计问题时明显优于其他4种算法,并表现出了较好的寻优能力,从而验证了CBES算法在工程应用的可行性.

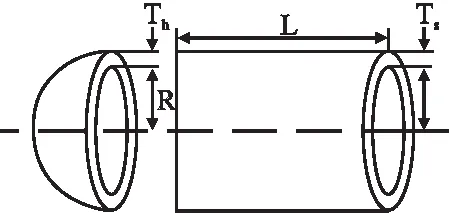
图2 压力容器模型Fig.2 Pressure vessel model

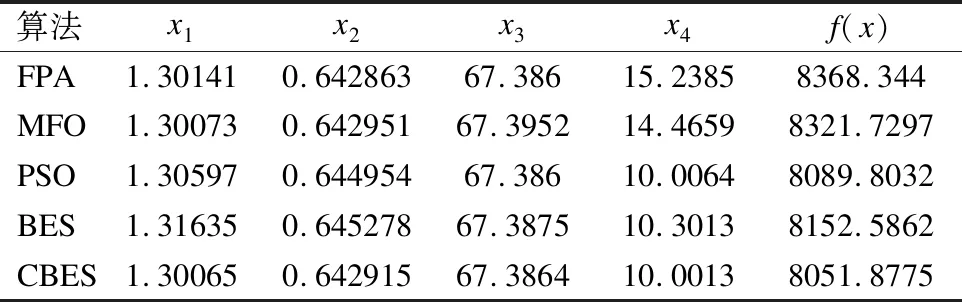
表3 压力容器设计问题求解结果Table 3 Results of solving pressure vessel design problems

7 结束语

针对基本秃鹰搜索算法的不足,本文提出了一种融合自适应惯性权重和柯西变异的秃鹰搜索算法(CBES).使用Tent混沌映射初始化种群,保留了种群的多样性;在秃鹰搜索空间猎物阶段通过引入自适应惯性权重来提高算法的局部搜索能力;并且在秃鹰俯冲阶段,对当前全局最优值使用柯西变异,降低算法陷入局部最优的可能性.将CBES、BES、MFO、FPA、PSO 5种算法放置在12个基准测试函数上进行实验对比,结果表明所提出的CBES收敛速度快且精度高.最后,将CBES应用到工程领域中,进一步验证了该算法的寻优能力以及可拓展性.在未来的研究工作中,将对融合自适应惯性权重和柯西变异的秃鹰搜索算法进行更加深入的理论研究,将其应用到更多的实际领域中.