圆柱体工件外径非接触测量及误差分析

贡乐凯，闫钰锋，王武，张振超

（1.长春理工大学 光电工程学院，长春 130022；2.北方导航控制技术股份有限公司，北京 100176）

圆柱体是应用非常广泛的构件形式，例如作为传动轴和轴承、齿轮等部件配合。随着加工技术的不断升级，对其检测精度也提出了更高的要求[1-2]，目前检测方法分为接触式和非接触式两大类。

接触式测量方法的代表是三坐标测量机，其通过与工件表面的接触力的方向及测头在坐标系中的位置，获得工件的三维尺寸数据，测量重复性精度可优于1 μm。这类接触式的测量方法可以实现高精度的测量，但在测量表面粗糙度要求较高的工件式，还存在因接触力导致工件表面变形的风险[3]。

非接触式测量方法主要包括激光测距法和数字图像处理法[4-8]。近年来，主要研究热点集中在高精度的激光位移传感器和先进的图像处理算法等方面。Kühnel 等人[9]设计了一种非接触圆度和圆柱度测量装置，采用双干涉仪结合高精度转台执行测量，减小了诸如工件偏心和倾斜等因素对测量的影响。国内的研究学者Gao 等人[10]提出了利用工业相机捕捉工件的侧面投影的方法来检测工件的外径尺寸。Chai 等人[11]使用激光位移传感器测量复和齿轮轴的同轴度，分离齿轮顶部的数据点后使用最小二乘圆及粒子群优化算法计算测量信息。

以上测量方法中，需对被测件的放置误差进行剔除，或对光学系统的装配要求较高。因此本文依据圆柱体工件在设计和加工时的回转特征基准，研究利用拟合被测工件的虚拟轴线的方法，有效抑制了被测工件的放置误差，可提高测量精度。并对影响测量精度的测量误差进行了分析，通过实验验证了测量系统的准确性和精密性。

1 测量模型及测量系统

1.1 测量模型

本文采用如图1 所示的结构测量圆柱体类型的工件。其中1 为升降台，2 为激光传感器，3 为位移台，4 为转台，5 为圆柱体工件。

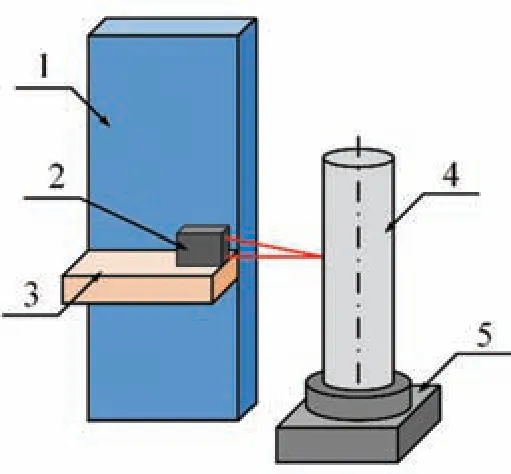
图1 测量设备结构示意图。

以升降台和位移台的机械零点为基准，建立绝对坐标系OA-xyz，如图2 所示。OA-z轴正方向沿升降台竖直向上，OA-x轴正方向沿位移台正向运动方向。

图2 绝对坐标系与测量坐标系。

在测量系统中，测量光束与OA-x轴平行，与转台回转轴线垂直且在同一平面内。设传感器在绝对坐标系中的位置为AS，AS=（xS，yS，H）。设转台在绝对坐标系中的位置为AR，AR=（xR，yS，0）。则转台的回转轴线的方向向量LR在绝对坐标系中的方向为LR=（0，0，1）。以AR为基准建立测量坐标系OM-xyz。OM-z轴正方向沿LR向上且平行于OA-z轴，OM-x轴正方向与OA-x轴同向，如图2 所示。理想情况下，在测量坐标系OM-xyz中圆柱体工件的轴线与LR重合且无偏心倾斜误差存在。此时点云截面为空间中的理想圆形。

但在实际测量中，圆柱体工件的轴线不与转台回转轴线重合，存在一定偏心距离与倾斜角度[12]，此时点云截面为空间中的椭圆形，如图3所示。

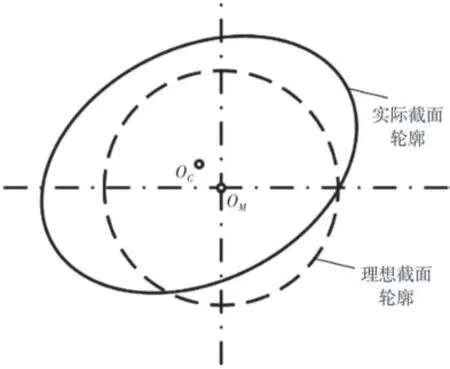
图3 实际测量模型

此时测量点在测量坐标系下的坐标为：

其中，d为传感器读数；Hj为传感器当前的测量高度；γ为转台转过的角度。单个圆柱体共J个测量截面，j=1，2，…，J。单个测量截面共I个测量点，i=1，2，…，I。为简化后续计算，令：

单个截面椭圆圆心可通过椭圆直接最小二乘算法拟合[13-15]计算得到。设目标函数为：

其中，a=[a，2b，c，2d，2e，f]T为未知的椭圆截面参数矩阵。施加等式约束4ac-b2=1 可得a矩阵各个值，进而得到椭圆的圆心坐标（xc，yc）：

得到各截面椭圆圆心坐标矩阵Oj=[xcj，ycj，zj]。可假设所有椭圆圆心均在圆柱体回转轴线上，则圆柱体回转轴线Lc在测量坐标系下的空间方程及其方向向量Lc可通过最小二乘法计算得到。设Lc的空间方程及其方向向量Lc分别为：

回转轴线Lc的延长线与测量坐标系OM-xoy平面的交点为（x0，y0）。结合各椭圆圆心坐标矩阵Oj计算如下：

由式（7）可以得到x0、y0、m及n。则测量坐标系中各测量点的外径为：

1.2 测量系统

如图4 所示，在本文使用的测量方法中，测量设备由1-高精度机械升降台、2-激光三角位移传感器、3-高精度气浮位移台、4-高精度转台和5-圆柱体工件组成。当转台携带被测圆柱体工件旋转360°后，传感器可采集到当前高度圆柱体的点云截面数据，经过扫描不同高度的圆柱体的表面后，可得到当前圆柱体工件的点云模型。测量时需确保传感器采集数据的时间间隔与转台转过固定角度的时间同步。

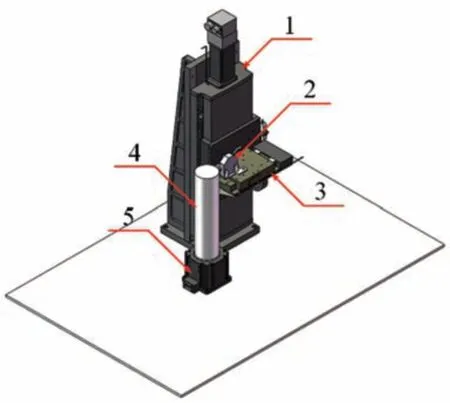
图4 测量系统配置

2 造成测量误差的主要因素

2.1 系统误差

系统误差包括传感器安装底座的制造误差及转台的安装误差。

首先，讨论由传感器安装底座的制造误差造成的系统误差。在OM-xoy平面中，由于传感器安装底座的制造误差使传感器偏离安装位置，测量光束及其延长线不能严格地与平面原点相交，存在一定的垂直距离，如图5 所示。

图5 OM-xoy平面与Osen-rt坐标系。

以传感器在OA-xyz坐标系中的理想安装位置为原点Osen建立传感器坐标系Osen-rt，Osen-r轴沿测量光束发射方向反向。Osen-t轴与Osen-r轴垂直。图5 中Osen为传感器理论位置，Osen1、Osen2、Osen3和Osen4分别为因制造误差导致的实际安装位置。

基于图5 所示关系，Osen-rt内的制造误差可分解为带有正或负方向的径向误差∆dr与切向误差∆dt，关系如下：

（1）Osen-rt第一象限，∆dr>0，∆dt>0；

（2）Osen-rt第二象限，∆dr<0，∆dt<0；

（3）Osen-rt第三象限，∆dr<0，∆dt<0；

（4）Osen-rt第四象限，∆dr>0，∆dt>0。

将带有正或负方向的径向误差∆dr及切向误差∆dt带入OM-xoy平面中。如图6 所示为传感器在Osen-rt第一象限下的情况。

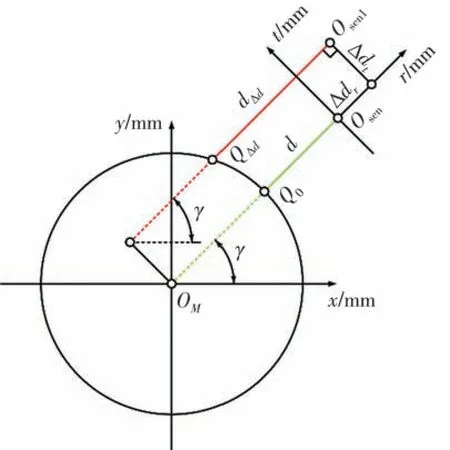
图6 光束发射点在Osen-rt第一象限。

Osen为理想情况下传感器位置，d为传感器理想读数。Osen1为传感器在Osen-rt第一象限下的位置，d∆d为带有制造误差的传感器实际读数。Q0为理想情况下的测量光斑位置。Q∆d为实际情况下的测量光斑位置，其在OM-xyz坐标系中的坐标表示为：

由于传感器安装底座存在制造角度误差δS，测量光束与OM-xoy平面之间存在俯仰角度，不能严格地与转台回转轴线保持垂直，如图7 所示。

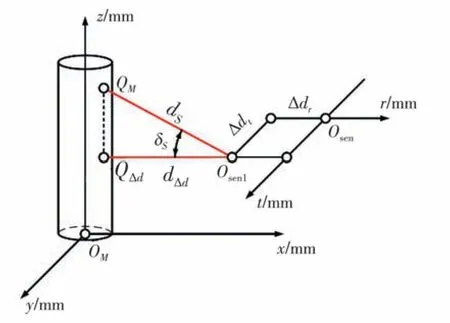
图7 测量光束与OM-xoy平面之间的夹角δS

因此，在式（9）中加入角度误差δS后，测量光斑QM在OM-xyz坐标系中的坐标表示为：

其中，ds为传感器在制造误差影响下的实际读数。则可以得到由传感器安装底座的制造误差造成的系统误差∆Ebase为：

在实际加工中，径向误差|∆dr|<0.03 mm，切向误差|∆dt|<0.03 mm，以及制造角度误差|δS|<0.2°。将∆dr、∆dt和δS分别作为自变量分析其对∆Ebase的影响。首先，将∆dr和∆dt作为自变量，令δS=0.2°为一固定值。

∆dr和∆dt对∆Ebase的影响如图8所 示。∆dr对∆Ebase的影响最为明显，直接影响测量结果；∆dt对∆Ebase的影响最小，对测量结果几乎不造成影响。

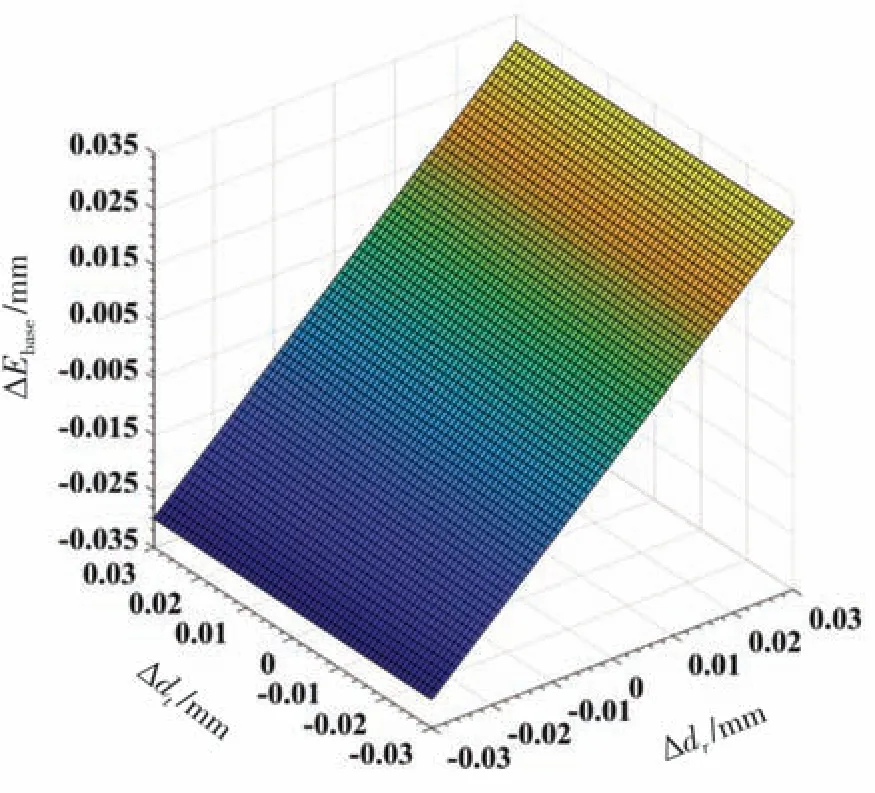
图8 ∆dr和∆dt对∆Ebase造成的影响。

然后，将δS作为自变量。令∆dr=0.03 mm，∆dt=0.03 mm，两值固定不变。δS对∆Ebase的影响如图9 所示。δS对∆Ebase的影响较为明显，会影响传感器读数的最后两位数值。

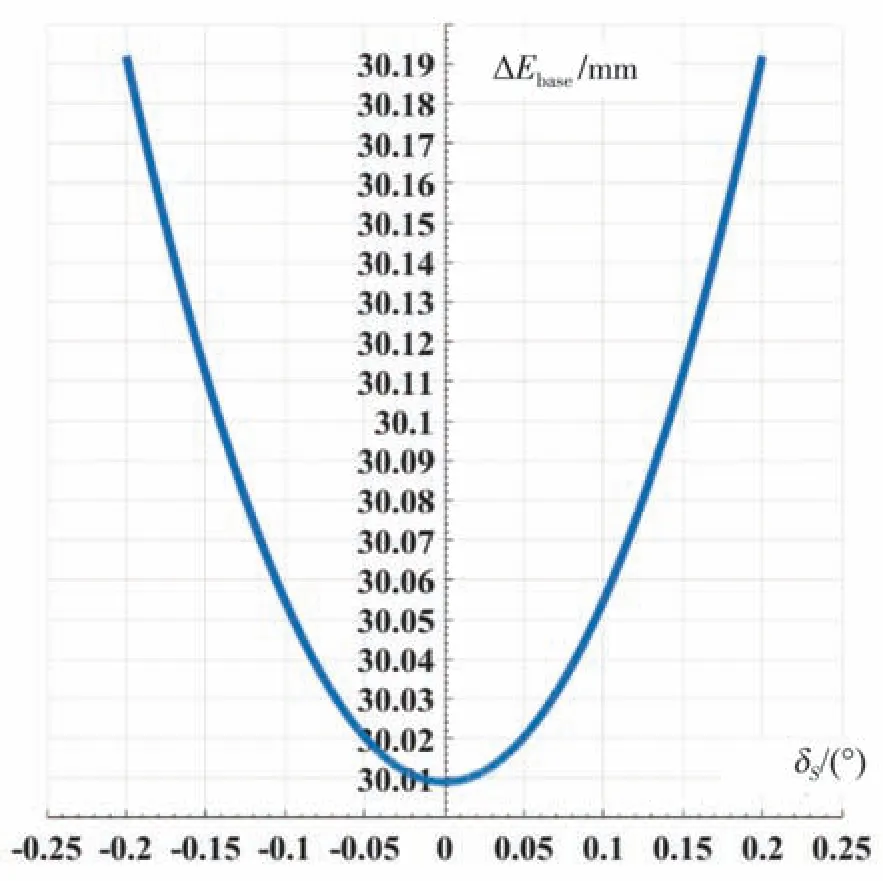
图9δS对∆Ebase造成的影响。

可通过位移台调整传感器在OA-xyz坐标系中的位置，调整传感器到转台回转轴线的距离，补偿∆dr的影响，可达到∆dr=0.5 μm。通过调整安装角度补偿δS的影响，可达到δS=2 arcsec。当圆柱体工件直径为100 mm 时，可得对∆dr及δS补偿后的∆Ebase=0.5 μm。

其次，讨论由转台的安装误差造成的系统误差。当转台携带圆柱体工件旋转时，测量光斑轨迹由测量光束与工件外壁形成，其形状受转台在OA-xyz坐标系中的安装误差的影响。当测量光束垂直于OM-z轴，∆dr=0，∆dt=0，δS=0°时，光斑轨迹为垂直于OM-z轴的空间圆形平面。当测量光束不与OM-z轴垂直，∆dr=0，∆dt=0，δS≠0°时，光斑轨迹为圆锥体。当测量光束不与OM-z轴垂直，∆dr≠0，∆dt≠0，δS≠0°时，光斑轨迹为不规则圆锥面，如图10 所示。

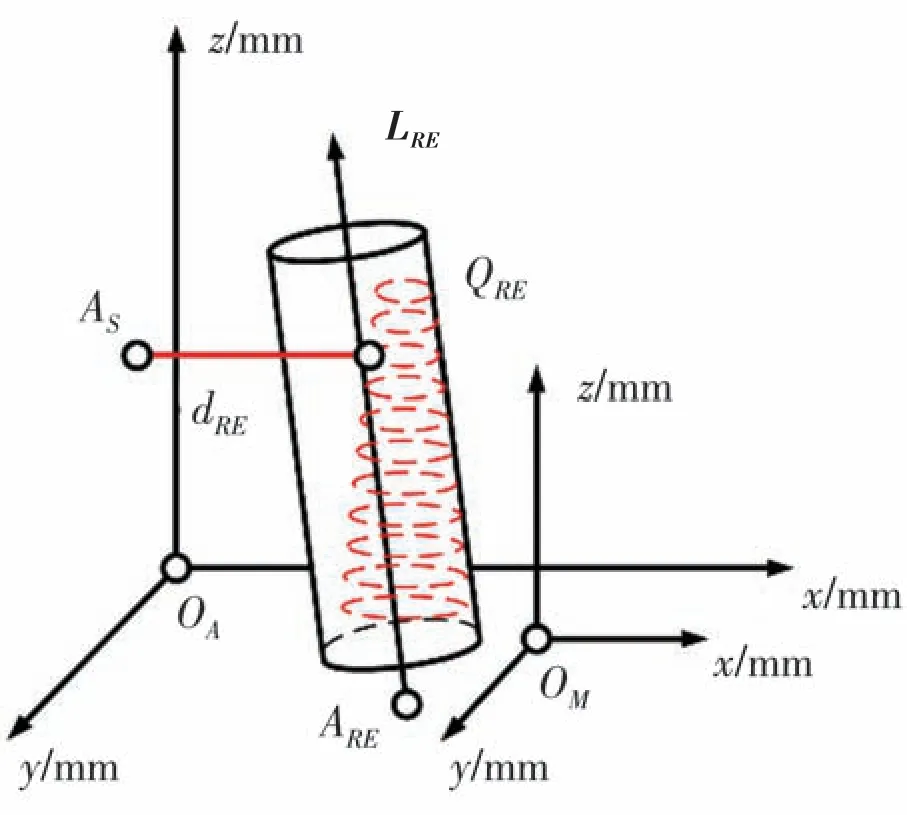
图10 测量光束的光斑轨迹。

此时，转台的回转轴线的方向向量LRE在绝对坐标系中的方向为LRE=（mR，nR，pR）。转台在绝 对坐 标系 中的 位置 为ARE，ARE=（xRE，yRE，0）。测量点QRE在OA-xyz坐标系中的坐标为QRE=（xS+dRE，ys，H），dRE为此时传感器读数，则QRE在OMxyz坐标系中的坐标表示为：

其中，θz为LRE与OA-z轴的夹角。设OA-z轴 单位向量为ze，ze=（0，0，1）。θz可由下式计算得到：

测量点QRE的外径值DRE可由公式（4）～（8）计算得到。则由转台的安装误差造成的系统误差∆ERE为：

其中，DR为传感器读数dRE以LR基准的计算结果。由于转台的安装误差造成的系统误差不为唯一值，故不将其作为固定值代入误差合成计算。

2.2 随机误差

传感器的直线度误差为∆Es=±2.5 μm。传感器的显示分辨率为0.01 μm，故其示值变动引起的局部误差为∆Eloc=0.01 μm。

将被测圆柱体放置于转台上测量时，圆柱体表面点云数据会受到转台径向跳动误差的影响。转台的径向跳动误差为∆ERT=3 μm。

高精度机械升降台负责控制传感器升降适应不同的测量高度，高精度气浮位移台负责控制传感器安装位置适应不同的圆柱体半径。高精度机械升降台的直线度误差为∆ELP=±3 μm，高精度气浮位移台的直线度误差为∆EDP=±0.25 μm。

则随机误差∆Erdm为：

可得∆Erdm=±4.93 μm。

2.3 系统总测量误差

根据2.1 节与2.2 节的分析，可以得到系统总测量误差合成公式：

可得测量误差∆Esum=±4.96 μm。

3 实验

3.1 测量系统的配置

图11 展示了测量系统的配置。该系统由1-高精度机械升降台、2-激光三角位移传感器、3-高精度气浮位移台和4-高精度转台组成。

图11 测量系统的配置

测量系统配置的性能参数参照表1～3。

表1 激光三角位移传感器性能参数

表2 机械升降台与气浮位移台性能参数

表3 转台性能参数

3.2 圆柱体样柱测量实验

如图12 所示。通过三坐标测量机获得样柱的外径及圆柱度测量的理论真值。通过与测量结果进行比较，评估系统的准确性和精度。自样柱最下端依次向上分别为第一圆柱、第二圆柱及第三圆柱。

图12 测量圆柱体样柱

根据前文介绍的测量原理，可以获得样柱外表面的三维点云。单个截面的测量点个数设置为I=128。根据样柱不同的高度设定不同的测量截面数量，第一圆柱共10 个测量截面，第二圆柱共9 个测量截面，第三圆柱共8 个测量截面。样柱的测量点云及其拟合椭圆圆心如图13 及图14所示。

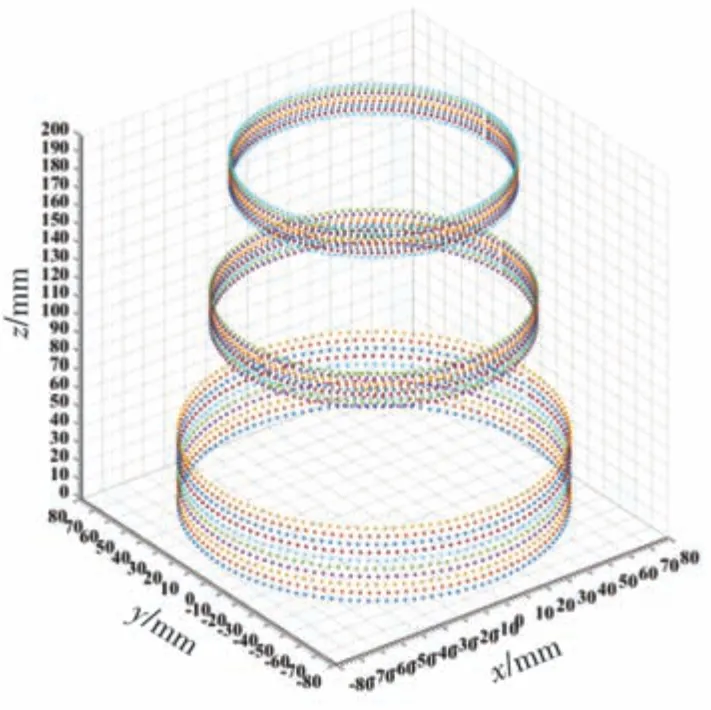
图13 样柱的测量点云

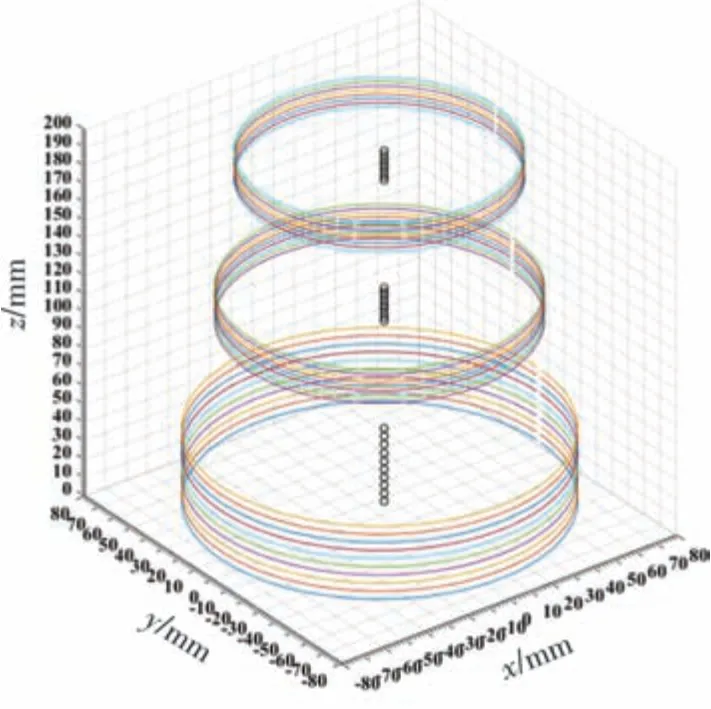
图14 各截面的拟合椭圆圆心

各截面直径测量残差结果如图15 所示。各测量点直径残差如图16 所示，放大倍率为1000倍。各截面直径测量残差结果及圆柱度测量残差结果如表4 及表5 所示。

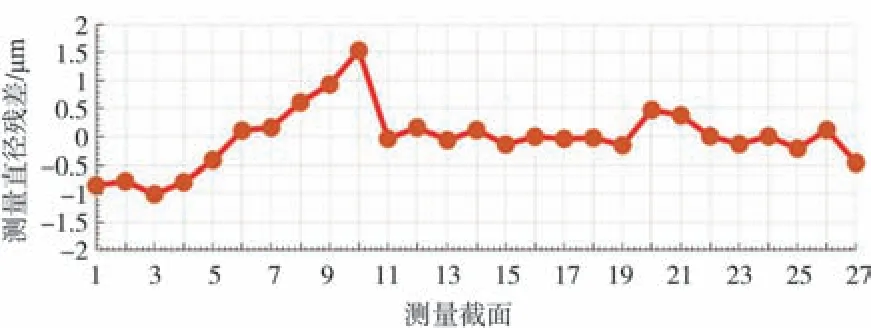
图15 直径残差测量结果

图16 直径残差

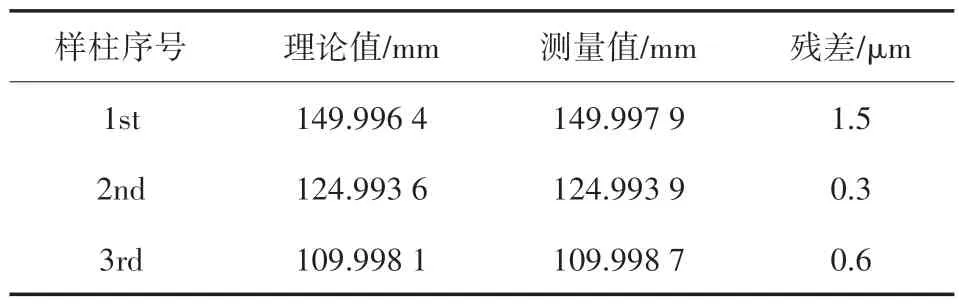
表4 直径测量残差结果

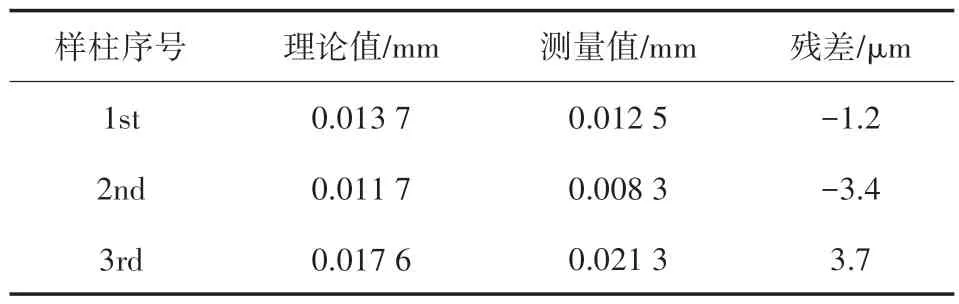
表5 圆柱度测量残差结果

可知测量结果均在误差分析范围内。实验结果可以验证本文测量方法的可行性。

3.3 测量范围及测量效率

根据高精度机械升降台的行程可知，该测量系统的轴向最大测量范围为300 mm。由表2 可知高精度气浮台的最大行程为50 mm，超过了传感器的最大测量范围，结合传感器的测量范围为30±5 mm，因此气浮台的使用范围为0～30 mm，则该测量系统可测量半径差值在30±5 mm 的圆柱体工件，且可根据实际需求更换更大量程的传感器和更大行程的横向位移台。

如表6 所示为在仿真实验中，直径为150 mm的圆柱体被测件与OM-z轴夹角为5°情况下，本文使用的拟合虚拟轴线算法与最小二乘圆算法的计算结果对比，共计4 个测量截面。表7 为计算结果的残差。

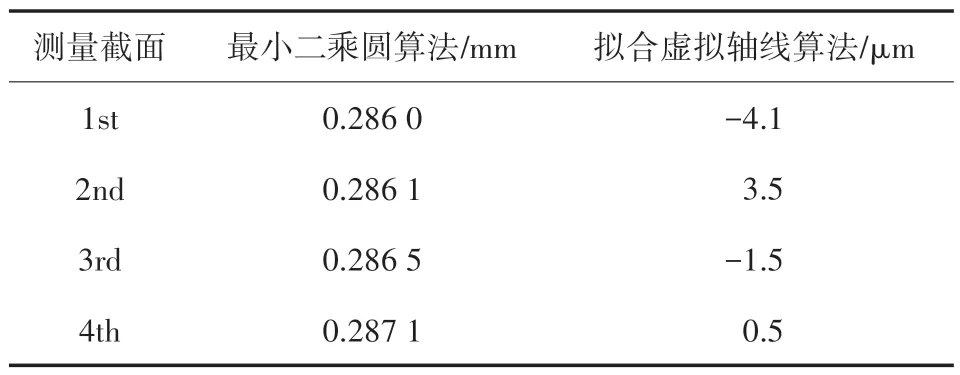
表7 计算结果残差

4 结论

本文提出了一套圆柱体工件外径测量系统。通过高精度位移台和激光位移传感器相结合的方式测量工件的基准轴和外径。分析了测量系统中的系统误差与随机误差，进行了具体实验验证了该系统的有效性。通过与三坐标测量机的测量结果对比，证明该测量系统的测量精度达到了±4.96 μm。

（1）所提出系统可以同时测量圆柱体工件的不同参数，如工件的基准、外径、圆柱度等，提高了测量效率。

（2）该系统通过对装配误差的补偿实现较高的测量精度。对于不同直径圆规同时测量，测量精度达±4.96 μm。

（3）该系统具有广泛的应用前景，对不同尺寸的圆柱体工件能保证良好的兼容性，同时降低了工件与测量仪器的安装难度，在实际测量场景下具有一定的应用价值。

（4）然而，由于测量系统对一些形貌复杂的圆柱体工件难以进行测量，所以具有一定的局限性，随着传感器技术的改进和发展，测量系统的范围和精度都可以得到提高。