基于耦合理论的城市燃气管网泄漏致灾模型研究*

张 倩 杨应迪

(安徽理工大学安全科学与工程学院 安徽淮南 232001)

随着城市化进程加快，居民对燃气的需求不断增加，管网的拓扑结构变得越来越复杂。燃气作为城市生命线的重要一环，燃气事故的发生会影响整个城市生命线，造成巨大的人员伤亡及财产损失。国内外对于风险耦合已有一定的研究，周洪波等[1]融合复杂网络和N-K模型，研究并确定了塔吊事故中的关键因素；Yue C等[2]考虑灾害的起源和演变，利用FLACS模拟和分析了液化天然气储罐泄漏灾害。王浅宁等[3]利用Mike系列模型分析了城市超标准洪涝灾害的影响。李浩然等[4]统计分析156起地铁重大事故，应用灾害链和复杂网络理论，分析了致灾因子对地铁风险防控的影响。彭琳等[5]应用ALOHA软件研究单因素对天然气管道泄漏扩散的影响。付邦稳[6]应用轨迹交叉理论分析管道失效机理，阐述了燃气管道失效的影响。

从上述文献可以看出，国内外关于风险耦合的研究已在不同方向取得了阶段性的成就，而对燃气管道事故的分析集中在泄漏本身及事故影响等方面，缺乏针对多因素耦合致灾机制及事故关键因素的研究探索。文章通过统计分析典型案例，建立燃气事故风险因素耦合模型并定量计算耦合风险值，分别确定了致灾因素之间的耦合关系及大小，其次引入社会网络模型进行网络中心度分析，进一步识别耦合中关键风险因素，为燃气安全事故的预防提供一定理论和实践支撑。

1 燃气事故安全风险耦合机理分析

燃气事故风险耦合主要为单因素耦合、双因素耦合及多因素耦合。以国家应急管理部、各省市相关网站、博燃网发布的事故案例为指引信息，再通过网络查找、文献查阅等方法，补全事故过程及原因，最终筛选出2016-2021发生的146起燃气事故，对这些案例进行分析归类，将燃气事故风险因素分为人-机-环-管四个一级因素以及20个二级子因素，风险耦合模型如图1。

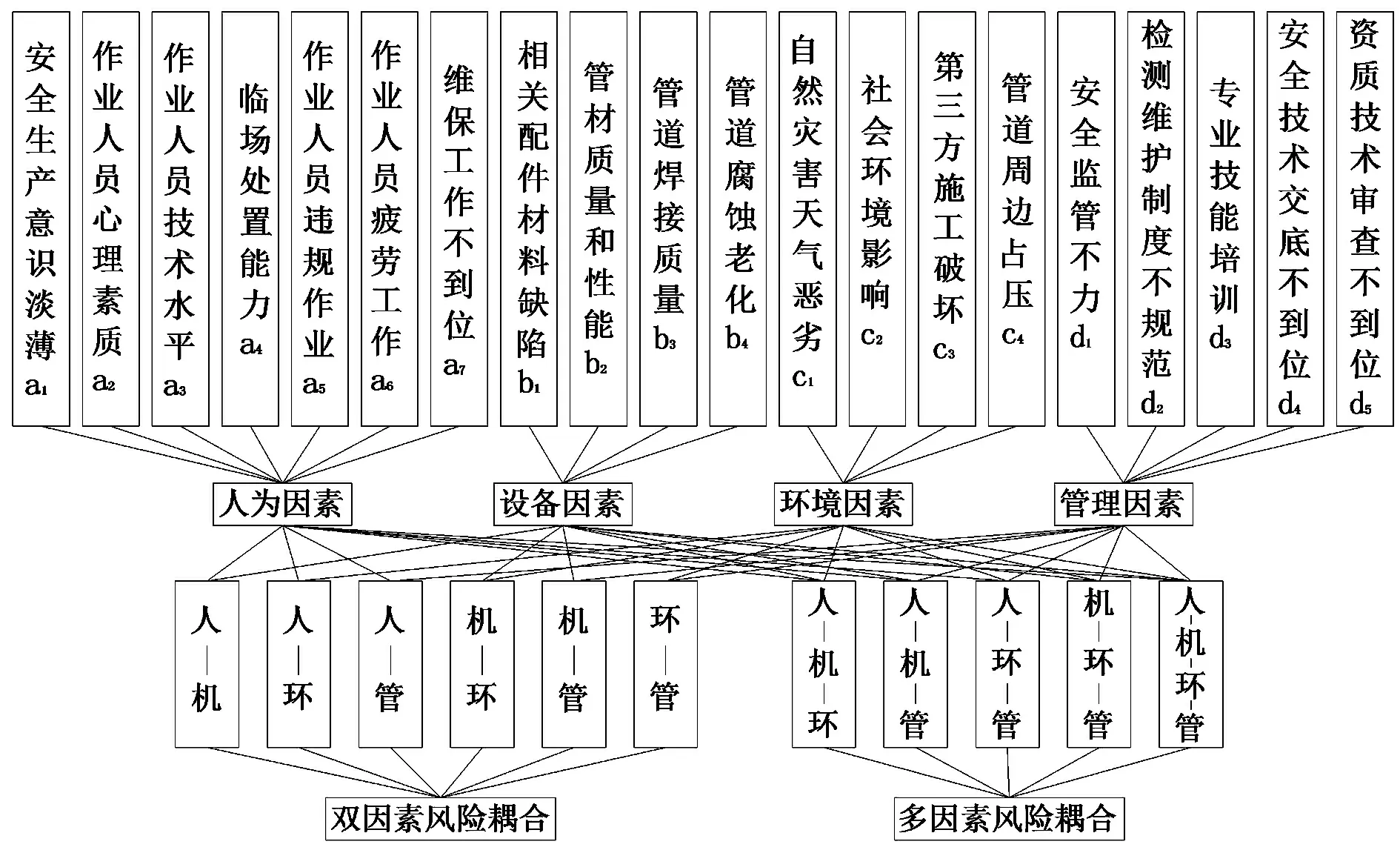
图 1 不同风险因素耦合模型

2 N-K模型与SNA模型下的燃气事故风险耦合分析

2.1 N-K模型构建

N-K模型由Kauffman提出，通过N-K模型可以计算系统风险因素间的交互式信息，比较不同风险因素耦合对系统的影响程度大小。很多学者用该模型解决复杂耦合系统问题[7-8]。燃气事故风险因素一旦突破自身极限值，就可能引起事故。因此利用N-K模型，计算风险因素耦合值，耦合值T的计算公式如下：

h=1，2，···；i=1，2，···；j=1，2，···；k=1，2，···；

(1)

式(1)中：T4指人-机-环-管完全耦合的数量化评估，结果越大耦合程度越高，风险越大。ph，i，j，k代表了当人、设备、环境和管理分别在h、i、j、k状态下燃气事故风险耦合发生的概率。

2.2 SNA模型构建

社会网络分析(social network analysis)通过构建网络模型，研究复杂个体之间的结构关系[9-10]。以燃气事故分析得到的二级风险因素构建致因网络，当不同因素在出现在同一个事故报告中，共现次数为1，得到共现矩阵。在Ucinet 6.0中输入共现矩阵，通过Visualize-NetDraw得到燃气事故致因网络图，如图2。节点代表燃气事故风险因素，连线表示风险因素间的直接联系，连线越粗则联系强度越强。

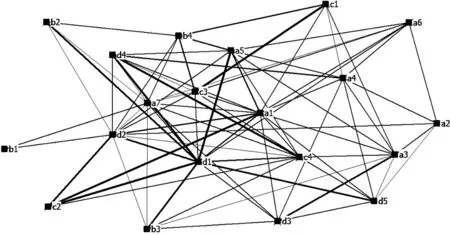
图2 燃气事故致因网络图

文章通过SNA的点度中心度、中介中心度和亲近中心度进行分析。点度中心度表示社会网络中各风险因素和其他因素的联系。点度中心度越高，对其他风险影响越大，该风险越关键。中介中心度反映风险因素对风险传递的影响程度，中介中心度高则表明其为控制系统风险传递的关键因素。接近中心度指节点在风险因素网络中的关键程度。接近中心度越高，风险因素越处于中心，越会影响其他因素。

2.3 N-K/SNA模型构建

N-K模型虽然降低了分析的主观偏好，但只能计算一级风险因素耦合值，无法进一步确定关键因素，而SNA模型能基于风险因素间的关系获得关键因素。将N-K和SNA融合，用N-K模型计算一级风险因素的耦合值，用SNA模型分析各二级因素的可达性，并对应到N-K模型，确定其潜在耦合形式。同时，利用SNA计算二级风险因素的中心度，得到关键风险因素排序，最后对关键因素进行耦合分析。

3 燃气事故风险因素实证分析

3.1 N-K模型计算结果分析

燃气事故的风险因素都有发生或未发生两种状态，用1或0表示，风险耦合形式有16种。对收集的146起燃气事故进行分类统计，得到了风险耦合发生的次数以及概率，见表1。

表1 燃气事故风险耦合次数及概率

为了得到T值，首先计算不同风险的耦合概率。人为因素不参与时事故发生概率：p0…=p0000+p0100+p0010+p0001+p0110+p0101+p0011+p0111=0.2123，同理算出其它耦合概率，代入式(1)，可计算出不同耦合方式下的T值，见表2。

表2 不同耦合方式下的T值

将结果从大到小排序：T4>T3，3>T3，1>T3，2>T2，2>T3，4>T2，4>T2，6>T2，1>T2，3>T2，5，对此结果分析可知：

(1)在燃气管道安全事故中，四因素耦合值最大，为0.2576，三因素耦合值普遍比双因素耦合值大，与燃气管道实际事故发生情况相符，说明参与耦合的风险因素越多，造成的风险影响越大。

(2)根据双因素风险耦合结果，机-管耦合风险最小，人-环耦合时风险最大，为0.0987，说明人-环耦合时更容易发生事故。由事故案例统计可知，恶劣的自然天气、第三方施工破坏等环境因素的出现都可能使管道损坏引起燃气泄漏。为避免人-环双因素耦合，要经常检查管道状态，保持管道运行良好。

(3)根据3因素风险耦合结果，主观因素(人-管)与环境因素耦合时风险最大，为0.1794，即在双因素耦合基础上叠加管理因素会更容易导致事故发生。而机-环-管耦合值0.0935，在三因素耦合结果中最小，且人-机-环>人-机-管，这说明人为因素和环境因素对燃气管道事故是否发生有着重要影响。

3.2 SNA模型计算结果分析

3.2.1 风险因素中心度分析 在Ucinet 6.0中得到风险因素中心度的计算结果，见表3。根据风险因素中心度结果分析可知：

表3 风险因素中心度

(1)安全生产意识淡薄a1、维保工作不到位a7、第三方施工破坏c3、安全监管不力d1等点度中心度较高，说明这些因素对其他因素有直接影响作用，并存在较高的脆弱性，对燃气事故具有较大的影响。

(2)由中介中心度结果可知安全生产意识淡薄a1、安全监管不力d1等主观因素的结果均较大，而设备、环境等客观因素的结果均较低，说明主观因素对其他节点的控制力较大，在风险传导中作用明显。

(3)从接近中心度结果可知设备原因接近中心度普遍较低，受其他因素影响较小，不是燃气事故的主要原因；而维保工作不到位a7、第三方施工破坏c4等因素的接近中心度较高，是燃气事故的主要原因。

3.2.2风险因素可达性分析 对风险因素进行可达性分析，剖析风险因素的潜在风险耦合形式。根据图2将20个二级风险因素的可达性对应到4个一级风险因素中，结果如表4所示。从表4可以看出，人的不安全行为a5、a7，管道的不安全状态b3、b4，不利的环境因素c3、c4以及管理因素d1、d2都可能导致人-机-环-管四因素耦合；人-机-环-管和人-环-管这两种风险耦合的比例较高。

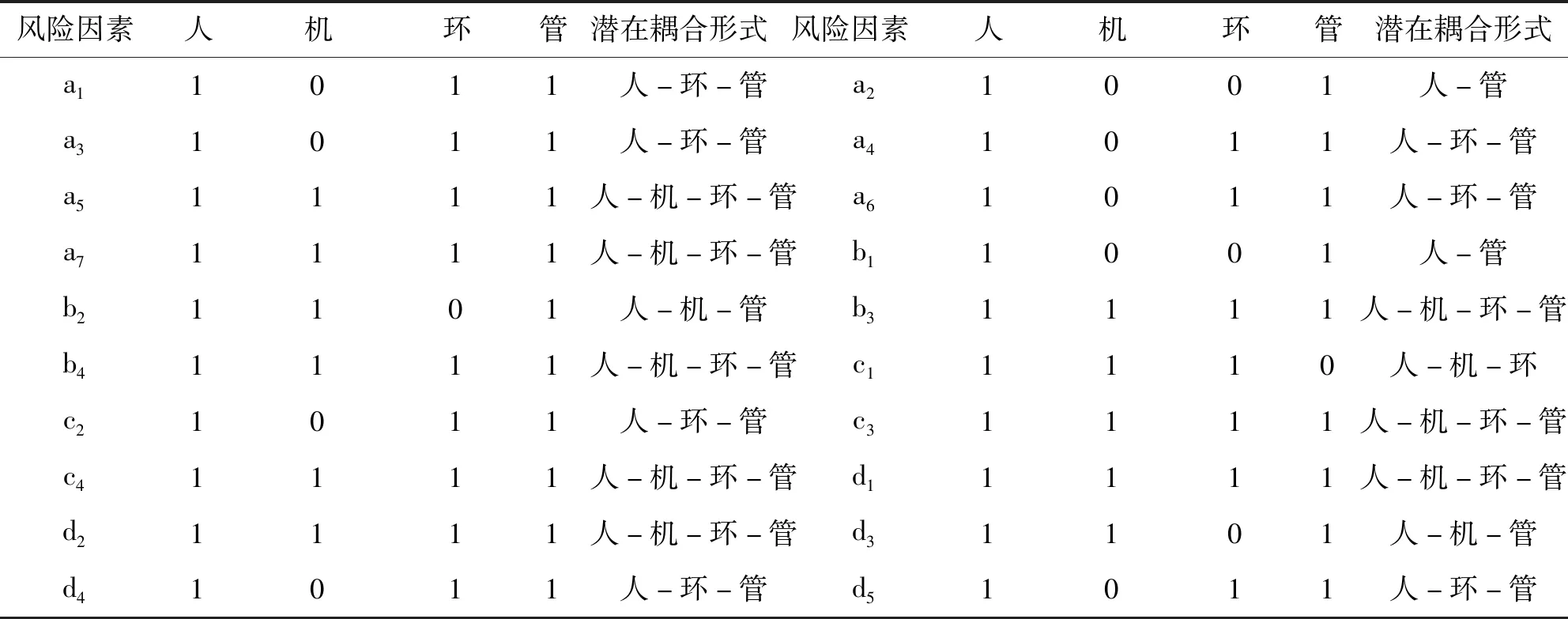
表4 风险因素可达性分析

4 结论

(1)文章对近年来发生的燃气事故进行风险辨识及耦合分析，构建了风险耦合模型及燃气事故致因网络图，为今后研究燃气事故致灾过程中耦合关系提供了参考。

(2)通过采用N-K模型与SNA模型相结合的方法，梳理各因素之间的耦合关系，量化风险耦合效应的危险程度，获得的关键致灾因素更加科学细致。从计算结果看，人的不安全行为是燃气事故发生的关键桥梁和控制枢纽，尤其是安全生产意识淡薄、维保工作不到位、安全监管不力这三个因素，对这些因素进行重点管控，避免这些关键风险因素出现，能有效降低耦合效应。