基于博弈论组合赋权的评价体系在大豆区域试验中的应用
昝凯,陈亚光,徐淑霞,周青,王凤菊,杨慧凤,郑丽敏,郭海芳,李明军,刘婷
(安阳市农业科学院/河南省优质大豆改良工程技术研究中心,河南 安阳 455000)
产量是区试中决定品种能否通过审定和推广的主要指标。在大豆品种同质化严重,尤其是单产提高幅度不大的形势下,大豆生产单位越来越看重百粒重、抗倒伏能力等特色指标的表现,只依据产量表现并不一定能够真实反映品种的综合性状和推广潜力,因此有必要采用适当方法将各农艺性状综合起来评价品种的优劣。作物综合评价体系中常用的评价方法多为灰色关联度、DTOPSIS 法、主成分分析、隶属函数法等的组合应用[1-5]。这类评价方法中,评价指标权重的确定是决定评价结果是否准确合理的关键。
作物综合评价中指标权重的确定可分为主观权重和客观权重两种类型。主观权重确定方法中,除专家直接赋权外,层次分析法是一种应用较广泛的确权方法,在工程决策、土地资源评价等领域应用广泛[6-8],作物种质资源综合评价中也有较多应用且取得了一定成果[9-12]。但不论是专家直接赋权还是层次分析法赋权,都存在赋权结果受评价主体意愿偏好影响的缺陷,赋权结果的说服力不够强。客观权重一般通过计算超标比确定指标的权重,可以反映出评价指标对评价结果的贡献度,但得到的权重仅考虑了个体指标的特征,赋权结果不一定能反映评价指标的重要程度[13]。客观赋权法中,熵权法在作物评价、工程决策、土地资源评价等领域中被广泛用于指标权重的确定[14-18],取得了较好的结果,但该方法依然没有解决客观权重存在的不足。基于博弈论的组合权重赋权法是一种能够将主客观权重相组合的有效方法,使评价指标的权重能体现评价主体的意愿,又能体现出评价指标对评价结果的贡献。该方法在工程决策、土地资源评价等多种学科的研究中应用广泛[19,20],西瓜、番茄等作物的综合评价模型中也有应用报道[21,22]。
层次分析法、熵权法和基于博弈论的组合权重赋权法在大豆综合评价中的应用报道较少,鉴于这3 类方法在其他领域有较好的应用效果,本研究尝试以2014 年河南省大豆区试参试品系为材料,构建基于博弈论组合赋权的综合评价体系对参试品系进行评价分析,探讨主客观组合权重在大豆区试中的应用效果,以期为大豆区试和育种过程中的品系鉴定和评价提供科学合理的方法。
1 材料与方法
1.1 材料
所用数据来源于2014 年河南省夏大豆区域试验,参试品系14个,对照品种1个,为豫豆22。由于本年度试验中参试品系的产量均高于豫豆22,根据《农作物区域试验操作规程大豆》(修订版)的相关规定,该区组对照采用15 个参试品种(系)产量的平均数,为便于比较,其他评价指标也以15 个参试品种(系)的平均值为对照,评价指标数据为12 个参试点的平均值。参试品种(系)的原始性状见表1。

表1 参试品种(系)原始性状数据
1.2 方法
1.2.1 建立层次结构模型 以筛选高产、抗逆、早熟、高蛋白质大豆品系为目标,根据层次分析法原理构造主要性状层次结构,形成目标层(A)、准则层(C)和指标层(P)。根据大豆种质资源特性,建立4 个准则层指标(Ci)13 个指标层指标(Pi)的大豆综合评价体系的递阶层次结构,详见表2。

表2 参试大豆品系综合评价体系层次结构模型
1.2.2 基于层次分析法和熵权法的权重确定 针对上下层各因子的隶属关系,从层次结构模型的第二层开始,对从属于上一层每个指标的同一层各指标用成对比较法和1—9 比例标度法将判断结果量化,对指标层和准则层各因素分别按影响上层目标的重要程度赋值,构造出准则层对目标层的比较判断矩阵A-C,指标层对准则层的比较判断矩阵C1-Pi、C2-Pi、C3-Pi、C4-Pi,计算基于层次分析法的指标权重[11]。基于熵权法的权重计算方法参见文献[7]。
根据矩阵的微分性质,集化模型的最优化一阶导数条件可转化为如下的线性方程组。
1.2.4 综合评分 采用极差法[24]计算参试品系评价指标的标准化值[μ(k)],并分别结合层次分析法、熵权法和基于博弈论的组合权重[u(k)]计算参试品系的综合评分(D)。
1.2.5 评价结果分析 对评价结果进行相关性分析并结合参试品系的审定情况验证评价结果的合理性和准确性,数据分析采用SPSS 20.0 软件进行。
2 结果与分析
2.1 评价指标选择的合理性
选取的评价指标包括产量、百粒重、单株粒数、单株荚数、生育期、株高、有效分枝、主茎节数、倒伏级、病毒级、杂色粒率(紫斑率、褐斑率和虫食率之和)、粗蛋白质含量、粗脂肪含量共13 个指标,涵盖了大豆区试中所考察的主要性状,具有很强的代表性,可以对参试品系的综合性状作出较全面的评价。由于本研究评价目标包含早熟要素,参试品系的株高最高为84.9 cm,处于生产上可接受的株高范围内,因此本研究将株高和生育期分别视为正向指标和逆向指标,不设中性指标,一方面避免可能因中性指标计算方法选择不合理对评价结果造成的偏差,另一方面也与评价目标和生产实际相符合。
2.2 层次分析法确定的指标权重
对构造的5 个判断矩阵进行一致性检验,结果(表3)显示,5 个判断矩阵的CR均小于0.1,层次总排序CR总=0.065 2<0.1,因此各评价因子具有较满意的一致性关系,说明构造的判断矩阵是合理的,指标层对目标层的权重可以作为决策的依据。

表3 判断矩阵与一致性检验结果
从表4 可以看出,准则层对评价目标的权重影响由大到小依次为C1(产量性状)、C3(抗性性状)、C2(生长特性)、C4(品质性状),权重分别为0.511 7、0.237 8、0.172 5 和0.078 0,产量性状占比超过50%,说明产量性状对大豆的综合表现仍然占主导地位,这与实际生产中追求提高大豆单产的目标是一致的。评价指标的权重由大到小依次为P2(百粒重)、P9(倒伏性)、P4(单株荚数)、P1(产量)、P10(病毒级)、P5(生育期)、P7(有效分枝)、P12(粗蛋白质含量)、P3(单株粒数)、P11(杂色粒率)、P8(主茎节数)、P6(株高)、P13(粗脂肪含量),其中排名前4 的指标权重均大于0.1,占评价指标总权重的60.36%,丰产性状和倒伏级权重较高,这与生产上大豆倒伏现象频发限制品种产量潜力发挥因而对大豆抗倒伏能力有较高要求的实际相符。
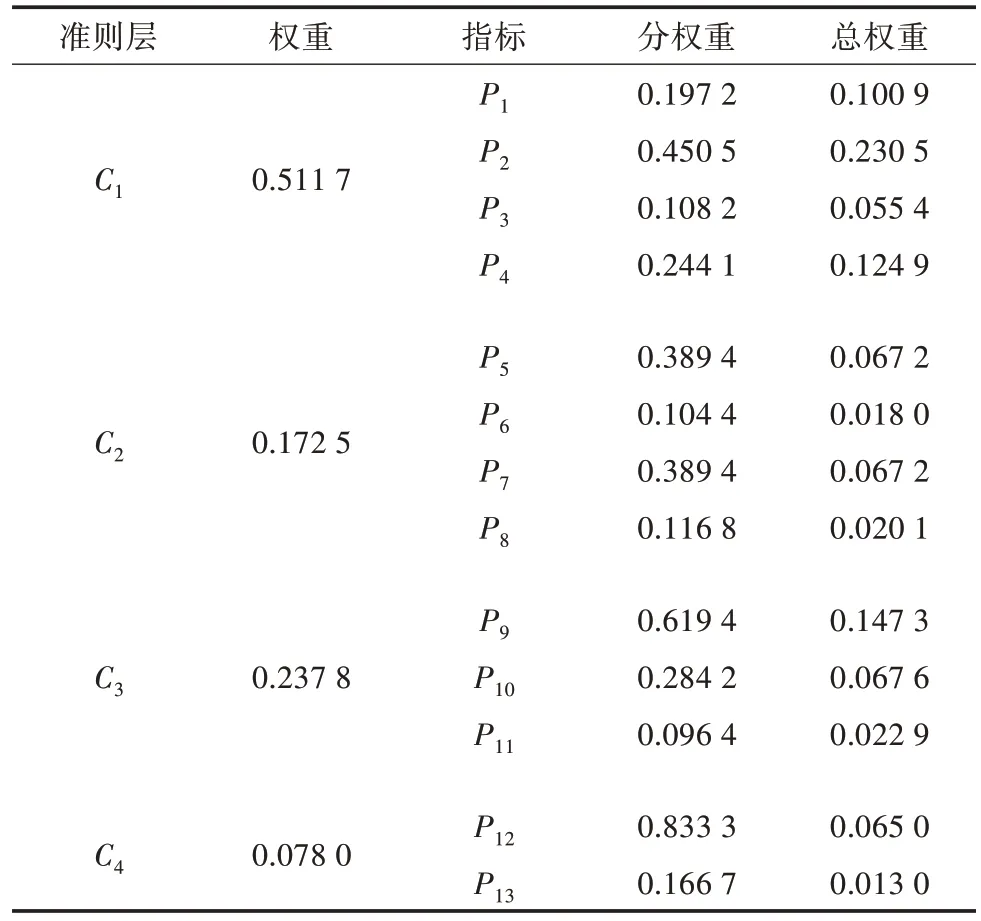
表4 层次分析法确定的评价指标权重
2.3 熵权法确定的指标权重
采用熵权法计算各指标的客观权重(表5),各评价指标权重由大到小依次为P10(病毒级)、P13(粗脂肪含量)、P4(单株荚数)、P8(主茎节数)、P3(单株粒数)、P6(株高)、P2(百粒重)、P9(倒伏性)、P11(杂色粒率)、P1(产量)、P5(生育期)、P7(有效分枝)、P12(粗蛋白质含量),熵权法得出的指标权重与层次分析法得出的权重排序有较大差异,2 种确权方法得到的评价指标权重关联系数为-0.17(P>0.05),说明基于评价指标的原始数据得出的客观权重并不能反映出评价指标的重要程度。

表5 熵权法确定的评价指标权重
2.4 基于博弈论的组合赋权法确定的指标权重
根据“1.2.3”提供的方法,可以计算出基于博弈论的组合权重中层次分析法和熵权法权重的分配系数分别为0.600 9 和0.399 1,进而可求得基于博弈论的各评价指标组合权重(表6)。评价指标权重由大到小依次为P2(百粒重)、P10(病毒级)、P9(倒伏级)、P4(单株荚数)、P1(产量)、P3(单株粒数)、P13(粗脂肪含量)、P5(生育期)、P7(有效分枝)、P12(粗蛋白质含量)、P8(主茎节数)、P6(株高)、P11(杂色粒率)。评价指标权重的大小排序与以上2 种方法均有差异,经相关性分析,组合权重与层次分析法和熵权法得出的指标权重相关系数分别为0.897(P<0.01)和0.282(P>0.05),均为正相关,说明基于博弈论的组合权重能够体现评价指标的重要性和客观性。

表6 基于博弈论的组合赋权法确定的评价指标权重
2.5 3 种确权方法下的综合评分
采用层次分析法、熵权法和基于博弈论的组合赋权法确权下的参试品种(系)综合评分见表7。由表7可知,不同确权方法下参试品种(系)评分和排名存在差异。对3 种确权方法下的综合评分进行t检验,结果显示3种确权方法下综合评分总体间的差异均不显著(表8),其综合评分的变异系数均高于产量变异系数。层次分析法确权下综合评分的最大值与最小值差异[(最大值-最小值)/最小值]为62.24%,熵权法确权和基于博弈论组合赋权下综合评分的最大值与最小值差异分别为83.56%和56.42%,而产量的最大值与最小值间的差异仅为14.93%,说明基于3 种确权方法的综合评价对参试品系优劣的区分度显著优于仅依据产量表现评价参试品系的方法。

表7 参试品种(系)不同确权方法下的综合得分和产量位次

表8 不同确权方法下综合评分的t检验
2.6 不同确权方法评价效果的比较
经相关性分析(表9),3 种确权方法下综合评分排名与产量(YD)排名均未达显著相关水平,说明3种确权方法均有效利用了评价指标提供的信息,能够科学评价参试品系的综合表现。基于博弈论的组合赋权法确定的综合评分排名与层次分析法和熵权法确权下综合评分排名的相关系数分别为0.872 和0.603,分别达极显著(P<0.01)和显著(P<0.05)水平,由此可以看出,基于博弈论组合赋权的综合评价体系既能体现出评价主体的偏好,又能较好地利用评价指标提供的客观信息,相较于单一的主观或客观确权法,可使评价结果具有较强的可信度和科学性。
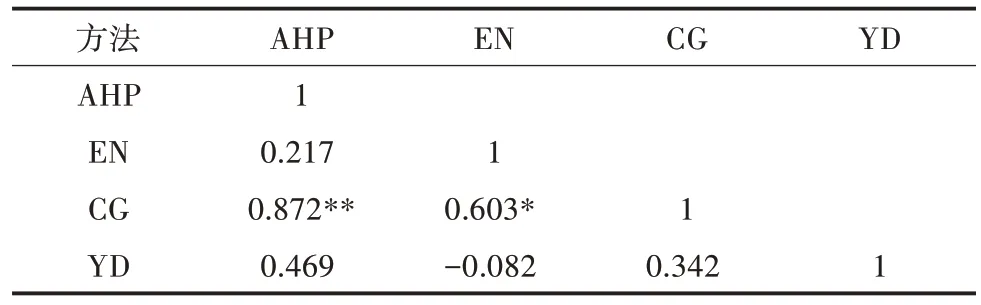
表9 综合评分与产量排名的相关性
2.7 组合赋权综合评价结果的合理性分析
由表7 可知,6 个参试品系CG 综合评分高于校准对照CK,分别为安豆5156、商豆1201、秋乐1205、中作X08110-1、驻豆03-56 和洛豆1号,其中秋乐1205、驻豆03-56 因对大豆花叶病毒病SC3 株系表现感病被一票否决而未能进入第二年区试,其他4个品系均成功晋级,最终通过国家或省级审定的有安豆5156(豫审豆2016002)、商豆1201(豫审豆2016002/国审豆20200029)、洛 豆1 号(豫审豆2017001/国审豆20190026)和濮豆1788(豫审豆2016003),都为第Ⅱ和第Ⅲ类群的品系。其中综合评分排名第1 的安豆5156 目前在河南、山东、安徽、江苏等大豆产区深受豆农喜爱,累计推广面积超6.7万hm2,其他审定品种在生产中也有优秀表现,说明基于博弈论的组合赋权法的综合评价结果与参试品系的实际表现有较好的一致性,评价结果是合理的。
3 讨论
3.1 组合赋权法在大豆区试中应用的必要性
大豆评价体系中评价指标的权重是决定评价结果是否科学合理的关键。目前,大豆综合评价体系中指标权重的确定主要为专家赋权和利用评价指标原始数据通过运算确定。专家赋权法确定的权重可以反映出评价指标在生产上的受重视程度,评价结果能够一定程度上代表品系的推广潜力,但多数情况下专家赋权结果中产量及产量相关性状权重占比达75%甚至更高[25,26],这样得出的结果与仅依据产量表现得出的评价结果基本相同,失去了综合评价的意义。客观赋权法根据原始数据揭示的信息进行确权,克服了人为干扰评价结果的不足,但指标的权重并不能反映指标的重要程度,如果仅依据客观权重进行综合评价,可能会使评价结果偏离生产实际,如本研究中洛豆1 号产量和百粒重指标均较高,十分契合当前黄淮海地区豆农的需求,但基于熵权法赋权的综合评分却最低。由此可以看出,主、客观权重都存在缺陷,通过将主、客观权重拟合实现互补,对提高综合评价的可信度和合理性十分必要,但在大豆综合评价中相关方法的应用研究较少。
3.2 基于博弈论组合赋权的综合评价体系在大豆区试中应用的合理性
基于博弈论的组合赋权法在作物区域试验中的应用鲜有报道,本研究将层次分析法和熵权法确定的权重利用基于博弈论的组合赋权法融合的综合评价体系在大豆区试中进行应用,结果表明,采用基于博弈论组合赋权的指标权重相较于层次分析法和熵权法单独确定的权重更符合生产实际和品种实际表现,组合权重评价结果与参试品系的表现有较好的一致性,说明该评价体系是可行的,既减少了评价过程中人为因素的影响,又能反映生产单位重视的性状表现较优良的参试品系的推广潜力,在大豆区试和育种单位的品系鉴定试验中有较广的应用前景。
3.3 基于博弈论组合赋权的综合评价体系在大豆区试中应用的局限性
基于博弈论组合赋权的方法是采用线性拟合的方式将2 种及以上确权方法确定的权重相融合,因此需要利用不同的方法分别计算出权重,计算工作量较大,开发相应的软件实现自动化将有助于该方法的推广应用。另外,前人在对大豆品系综合评价时选取的评价指标各不相同,但大多包含产量性状、抗逆性状等,本研究选取的评价指标涵盖了河南省大豆区试中考察的产量性状、抗逆性状、生长特性、品质性状等大多数指标,具有较强的代表性和综合性,但对评价指标原始数据的标准化处理中,由于中性指标的标准化处理需要一个理想值,且处理方法也有多种,应用时该如何选择还有待进一步探讨,因此本研究没有设置中性指标。在今后的应用中还应根据评价目标进一步优化评价指标,并对评价指标的正向化、逆向化和中性化合理分类,选择适当的方法对指标数据进行标准化,以使评价结果更加准确合理。
4 小结
本研究利用基于博弈论的组合权重赋权法将层次分析法和熵权法确定的权重结合,构建了大豆品系综合评价体系,并在大豆区试中进行了应用分析。结果表明,基于博弈论的组合权重赋权法在大豆区试中的应用是必要且可行的,其评价结果可较全面地反映参试品系的实际表现和推广潜力。开发相关软件实现自动化以克服该方法计算繁杂的缺点后,可以使该方法在大豆区试和各育种单位的品系鉴定试验中得到广泛应用,对大豆品种(系)的实际表现和推广潜力作出合理、准确的评价。

