地铁自动检票机故障分析及可靠性研究
徐余明,黎家靖,张宁,石先明,刘利平,胡祖翰
(1.中铁第四勘察设计院集团有限公司,湖北 武汉 430063;2.东南大学 智能运输系统研究中心,江苏 南京 210018)
随着地铁运营设备数量不断增加,如何在已有历史故障数据的基础上准确分析设备可靠性变化趋势已成为研究热点。关于设备的可靠性研究目前主要集中在车辆设备[1-3]、供电设备[4]、列车系统[5]、站台门系统[6]等方面,且大多采用单一的威布尔分布构建可靠性模型。此外,有学者对地铁AFC系统及自动检票机设备开展了相关研究,但多为系统架构及平台设计[7-8]、故障时刻预测[9]、无故障运行时间预测[10]等,目前结合自动检票机故障特点对其可靠性进行分析的研究相对较少。基于此,本文在对自动检票机进行故障分析的基础上,基于混合威布尔分布构建可靠性评估模型以克服单一威布尔分布误差较大的问题。通过建立非线性最小二乘参数优化估计模型并利用粒子群优化算法进行参数寻优,拟合自动检票机的可靠性函数变化曲线。
1 地铁自动检票机故障分析
地铁自动检票机(Automatic Gate Machine, AGM)作为AFC系统重要的终端设备之一,将车站划分为付费区与非付费区并控制乘客进出[11]。自动检票机由机械部件和电气部件两部分组成,见图1。自动检票机的内部结构复杂且故障形式多样,分析其故障变化规律及影响因素是进行可靠性研究的重要前提。
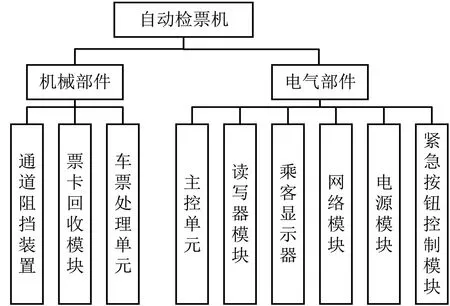
图1 自动检票机设备组成
1.1 设备故障变化规律
故障率曲线反映了设备故障的内在变化规律和机理,统计研究发现,大多机械部件的故障率曲线为“浴盆曲线”[12],分为早期故障期、偶发故障期和耗损故障期3个阶段,见图2。此外,部分电气部件或复杂设备在实际运行过程中的故障率曲线往往是以下几种故障特征曲线中的一种或几种的组合[9],见图3。由图2和图3可以看出,机械部件与电气部件之间的故障率曲线存在一定差异,设备的故障率与其自身材料性质有较大联系。

图2 机械部件故障率曲线

图3 电气部件与复杂设备5种故障率曲线
1.2 自动检票机故障影响因素
自动检票机设备受到各种因素的影响,在一段时间后会出现不同程度的损耗或故障现象。导致自动检票机发生故障的影响因素主要包括内部因素和外部因素,其中内部因素包括设备自身状况、设备维修水平及成本等,外部因素包括设备运行环境、乘客行为及客流量等。
(1)设备自身状况的影响
自动检票机设备自身质量的好坏是设备故障的首要影响因素。设备的设计缺陷、生产工艺、部件材料等会对设备质量造成直接影响,不同设备厂商或同一厂商的不同批次生产的设备在可靠性指标、生产标准、安全性能等方面也会有所差异[13]。
(2)设备维修水平及成本的影响
自动检票机设备故障后能否修复以及修复到故障前的何种程度取决于维修人员的专业素养、技术水平、工作能力、维修经验等。此外,为降低设备运维成本,部分地铁公司选择将设备维护和维修业务部分或全部委外给相关设备维修管理公司,这对设备维修效率、修复时长等产生了一定影响。
(3)设备运行环境的影响
设备运行环境往往是设备故障的潜在影响因素。自动检票机设备的运行环境包括外部大环境和内部小环境,外部大环境如强降雨、大风、地震等自然灾害;内部小环境如设备的安装位置、周围温度及湿度等。设备故障还受季节因素的影响,不同季节的自动检票机故障次数不尽相同。
(4)乘客行为及客流量的影响
自动检票机主要由乘客直接使用,乘客的异常或违规操作会加快设备故障或损坏。客流量与设备故障也存在一定联系,客流量大、乘客使用频率高的自动检票机设备,其故障发生频率也相对较高。
本文结合自动检票机设备组成、故障影响因素及实际故障数据,将其故障类型分为扇门故障、回收模块故障、读写器故障、乘客显示器故障及网络故障五类,其中前两类属于机械类故障,后三类属于电气类故障,自动检票机故障类型及原因见表1。

表1 自动检票机故障类型及原因
2 混合威布尔分布模型
在设备可靠性分析中,威布尔分布常被用于描述各类机械产品或电气产品的失效数据分布规律。自动检票机内部同时包含机械部件和电气部件,故障失效数据往往存在多种失效模式,传统的单一威布尔分布难以准确描述其故障变化规律。为更好地拟合自动检票机的故障失效数据,本文以二参数威布尔分布为基础,使用多重混合威布尔分布对其进行可靠性建模,以提高模型的准确性和适用性。
2.1 二参数威布尔分布
威布尔分布分为二参数威布尔分布和三参数威布尔分布两种形式,本文以二参数威布尔分布为基础定量研究设备可靠性。若设备的失效数据服从二参数威布尔分布,其可靠度为:
(1)
式中:t表示设备的运行时间,t≥0;η,β分别为尺度参数和形状参数,且η、β均大于0。
设备的不可靠度F(t)、失效概率密度函数f(t)、故障率λ(t)分别为:
(2)
(3)
(4)
寿命期望值(MTTF)表示设备无故障平均运行时长,以E(t)表示:
(5)
则设备的剩余寿命函数u(t)为:
(6)
2.2 混合威布尔分布建模
混合威布尔分布可更加准确地描述设备在多种失效模式共存情况下的可靠性变化规律。假设自动检票机的故障失效数据存在n种失效模式,则可将自动检票机看成是一个由n个子体组成的总体,每个子体具有独立的失效分布,则总体的失效概率密度函数为:
(7)

由式(2)、式(3)可得出可靠度R(t)和失效概率密度函数f(t)之间存在微积分关系:

(8)
将式(7)代入式(8)中可得出:
(9)
式中:Ri(t)为第i个子体的可靠度。
若自动检票机的各子体服从威布尔分布,则设备的n重混合威布尔分布可靠性模型如下:
(10)
式中:ηi,βi分别为第i个子体的威布尔分布尺度参数和形状参数。
2.3 基于PSO算法的模型参数优化估计
由式(10)可知,n重混合威布尔分布共有3n-1个未知参数,本文基于误差平方和最小思想,在已有自动检票机实际故障数据的基础上构建非线性最小二乘参数优化估计模型:
(11)

式(11)的参数优化估计模型属于有约束模型,使用粒子群优化算法(Particle Swarm Optimization, PSO)对其进行最优参数求解,以参数优化估计模型中的误差函数作为适应度函数更新各粒子的位置和速度。为提高粒子寻优效率和减少寻优时间,使用序列最小二乘法(SLS算法)粗略估计混合威布尔分布模型的初始分布参数。具体参数估计流程见图4。

图4 混合威布尔分布的参数估计流程
3 实例验证
本文以南京地铁油坊桥车站某自动检票机2016年全年的故障失效数据为例进行实例验证,按照故障时间先后顺序统计后的故障失效数据见表2,其中机械类故障有36条,电气类故障有14条。

表2 自动检票机的故障失效数据
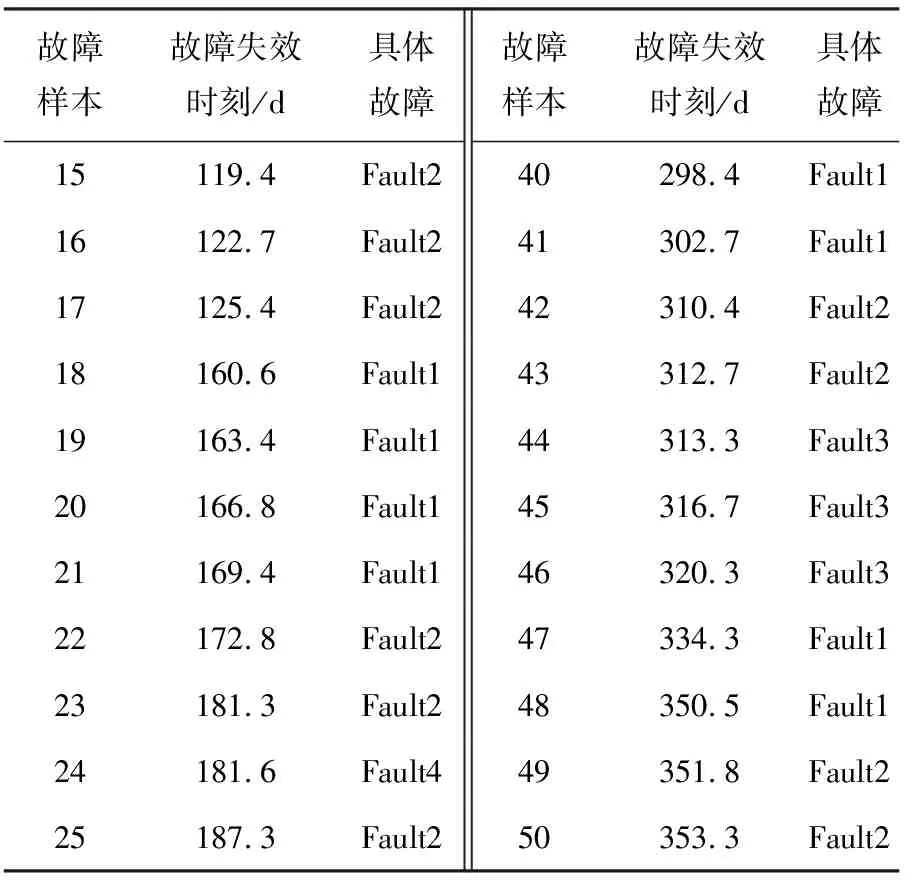
续表
考虑到地铁自动检票机同时存在机械类故障和电气类故障,本文根据式(10)建立两重混合威布尔分布模型进行可靠性分析,可靠度函数为:
(12)
3.1 PSO参数寻优
由式(12)可知共有p1、η1、β1、η2、β25个未知参数,SLS算法粗估计值为p1=0.303 1、η1=273.0、β1=5.884 9、η2=200.0、β2=1.405 0,以该估计值构造初始粒子群。将式(12)代入参数优化估计模型中得到最小化误差优化目标函数并将其作为适应度函数,设置粒子群数量为30,PSO算法迭代优化结果见图5。

图5 PSO算法的迭代优化结果
由图5可知,经过500次迭代优化后,适应度值从0.019 455下降至0.008 781,约减少55%,因此粒子群算法能有效优化混合威布尔分布的模型参数并减少模型误差。
3.2 模型误差分析
使用均方根误差(RMSE)、平均绝对百分比误差(MAPE)、皮尔逊相关系数作为各分布模型的评价指标。表3为单威布尔分布、混合威布尔分布、基于PSO算法的混合威布尔分布得到的参数估计结果及对应误差。由表3可知,混合威布尔分布的各项误差均优于传统的单威布尔分布,在多种失效模式共存的情况下具有明显优势。由于使用粒子群算法对混合威布尔分布进行参数寻优,因此基于PSO算法的混合威布尔分布的误差最低,其RMSE、MAPE分别达到了0.018 726、0.063 120。
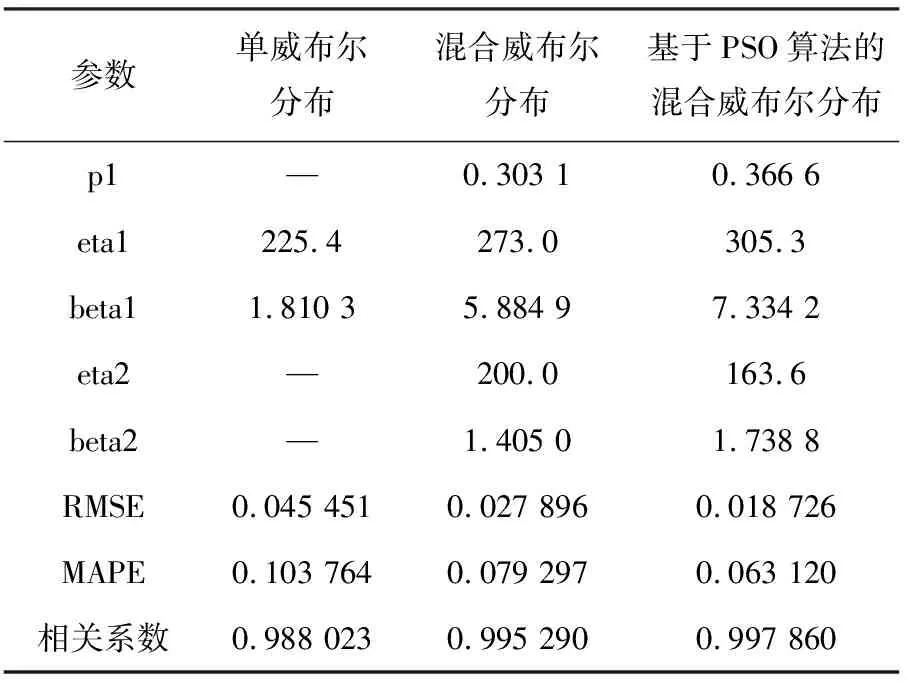
表3 三种分布模型的参数估计结果及误差
根据表3中各分布的参数估计结果绘制出对应模型的拟合曲线,见图6。由图6可以看出,基于PSO算法的混合威布尔分布能准确拟合早期、中期与后期的故障失效数据,中位秩可靠度观测值均匀分布在拟合曲线的两侧,其拟合效果最好。

(13)
表4为各分布的K-S检验结果,置信度取95%,则临界值Dm,a=D50,0.5=1.36/500.5=0.192 3。当Dmax 表4 K-S检验结果 此外,为体现基于PSO算法的混合威布尔分布的模型适用性,选取同年同站点的另一台同类型自动检票机的故障失效数据进行试验,相关误差如表5所示。由表5可知,基于PSO算法的混合威布尔分布的各项误差均为最优,K-S检验统计量Dmax最小,说明该模型能较好拟合同类型自动检票机的故障失效数据,具有一定的适用性。 表5 同类型自动检票机的模型误差 根据表3中的参数估计结果及误差,由基于PSO算法的混合威布尔分布的参数估计结果得到自动检票机的可靠度R(t)、不可靠度F(t)、失效概率密度函数f(t)分别为: 为进一步对进行自动检票机可靠性分析,分别绘制出其可靠度R(t)、不可靠度F(t)、失效概率密度函数f(t)、故障率λ(t)、剩余寿命函数u(t)的图形,见图7。由图7可知,随着服役时间的增加,自动检票机的可靠度逐渐降低,不可靠度逐渐升高,剩余寿命逐渐减少,符合设备实际运行情况和客观变化规律。失效概率密度函数曲线呈现出一定波动,在第300 d左右取得最大值,表示自动检票机运行至该时间点附近其不可靠度变化速率最快,发生故障失效的设备数量最多。此外,自动检票机在服役前期和中期性能较好且稳定运行,后期出现设备老化和耗损问题,因此其故障率在前期和中期处于较低水平,后期开始持续上升,故障率曲线整体呈上升趋势,服役时间越长,故障率越大,发生故障的可能性也越大。 (c) 失效概率密度函数 (1)本文通过对地铁自动检票机进行故障分析,探讨了其故障变化规律及故障影响因素。考虑到自动检票机内部包含机械部件和电气部件,故障失效数据存在多种失效模式,使用多重混合威布尔分布对其进行可靠性建模以提高模型拟合精度。 (2)基于误差平方和最小思想构建有约束的非线性最小二乘参数优化估计模型,使用SLS算法粗略计算分布参数初始值并以粒子群优化算法进行模型最优参数求解。 (3)通过实例验证,本文提出的基于PSO算法的多重混合威布尔分布具有一定适用性,对自动检票机故障失效数据具有更好的拟合效果,其RMSE、MAPE、皮尔逊相关系数均优于传统单威布尔分布与混合威布尔分布。本文研究结果可为自动检票机的可靠性分析及日常维护提供参考,具有一定实际意义。

3.3 可靠性分析
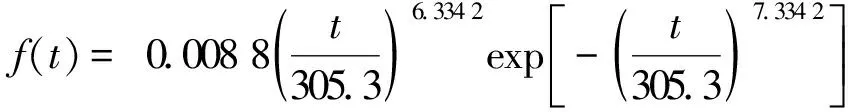

4 结论

