一种基于二元多项式的多秘密共享方案
韩妍妍 谢定邦 郭 超 赵 洪
1(北京电子科技学院通信工程系 北京 100070) 2(西安电子科技大学通信工程学院 陕西 西安 710071)
0 引 言
Shamir[1]和Blakley[2]分别基于拉格朗日插值多项式和映射几何首次提出秘密共享方案。此后,秘密共享作为现代密码学的一个重要研究方向,在门限加密、门限签名和安全多方计算等领域都有着很好的应用。近年来,随着大数据、云计算,尤其是区块链技术迅速发展而引出的密钥管理问题,秘密共享技术作为解决方法将发挥更加重要的作用。Shamir秘密共享方案[1]包括系统秘密分发和秘密重构两个算法。主要思想是将秘密S分割成若干份秘密份额,并且具有属性:(1) 任意t或大于t份秘密份额即可恢复秘密S;(2) 任意少于t份秘密份额无法获得秘密S的任何信息。秘密共享技术不仅可以防止由于单个保管者的权力过于集中而导致的权威欺骗,而且秘密的分布式管理能有效保证重要数据的安全和健壮性。
Shamir秘密共享方案中,单次秘密共享过程仅可共享单个秘密;方案一次性使用;若要共享一个新秘密,分发者必须重新计算和生成新的秘密份额,并重新下发秘密份额给所有参与者。当多个秘密需要共享时,分发者计算和传输秘密份额就会消耗大量资源导致方案效率低下。He等[3]针对上述问题提出多阶段多秘密共享方案,使用公共移位技术和单向函数可按预定顺序重构多个秘密。此后,多秘密共享方案经过不断发展,多种方案被相继提出:按预定顺序重构或任意次序异步重构的多秘密共享方案[4-7],一次并行重构多个秘密的多秘密共享方案[8-10]等。
二元多项式通常被用来构造可验证的秘密共享方案[11-13]。近年来,基于二元多项式设计的秘密共享方案扩展到了许多密码学场景,例如: 多方量子密钥交换协议[14]、秘密共享可欺骗识别方案[15]、异步多秘密共享方案[16]、图像秘密共享方案[17]等。传统秘密共享方案中,方案实际部署往往会受到非参与者的外部攻击,秘密重构的过程中必须要引入额外的密钥协商机制,进而建立重构者之间的安全通道,这使得方案变得复杂。Harn等[18]基于二元非对称多项式提出受保护的秘密共享方案(PSS),参与者收到的秘密份额不仅可以用于产生子秘密,还可产生任意参与者之间的会话密钥,不用额外的密钥协商机制就构建了参与者间的安全通道。PSS方案与Shamir秘密共享方案相比有着近似的计算复杂度,并且该方案不基于任何计算性假设,是信息论安全的,但是其方案没有扩展到多秘密共享场景。Harn等[16]第一次提出基于二元非对称多项式的多秘密共享方案, 继承了PSS方案参与者间安全通道的性质,并且是任意次序异步恢复的多秘密共享方案。Zhang等[19]指出文献[16]的多秘密共享方案无法抵御t-1个参与者内部合谋攻击,当参与者成功重构一个秘密后,t-1个参与者即可通过获得的秘密份额合谋计算未重构的所有秘密;Zhang等[19]基于二元多项式构造了多秘密共享方案,通过构造额外的二元对称多项式,生成会话密钥保证参与者间安全通道,扩展方案在满足文献[16]贡献的同时,异步恢复多秘密。但是其方案会增加分发者计算和秘密份额传输开销,而且不可抵抗半诚实参与者攻击。
本文提出基于二元非对称多项式的多秘密共享方案,方案一次可重构多个秘密,在大秘密分割共享和多秘密共享方面都有较好的应用场景;继承了文献[16]多秘密和安全通道的特性,又解决了其受到的安全攻击问题。方案可进一步设计成门限加密和门限签名算法,进而可结合当前区块链、电子投票等应用场景来推动技术发展。本文方案参与者获得的秘密份额不仅可以产生子秘密,并且可以生成会话密钥,用于保护在秘密重构过程中重构者间的信息交换。通过安全性分析,本文方案可抵抗内部合谋攻击和重构过程中的外部攻击。
1 预备知识
1.1 Shamir秘密共享
Shamir秘密共享方案包含两个算法:秘密分发和秘密重构。假设可信分发者为D,参与者集合U={U1,U2,…,Un},p是大素数,所有计算都在p阶有限域上。
秘密分发: 分发者随机选择一个t-1次单变量多项式f(x)=a0+a1x+a2x2+…+at-1xt-1modp,其中秘密s=a0∈GF(p),ai∈GF(p),i=1,2,…,t-1。D计算n个秘密份额s1=f(1),s2=f(2),…,sn=f(n),并将n个秘密份额分别通过秘密通道发送给参与者Ui(i=1,2,…,n)。
秘密重构: 任意大于或等于t个份额即可恢复秘密,假设有m(t≤m≤n)个参与者恢复秘密,参与者相互之间交换份额,获得t个份额的参与者可通过拉格朗日插值公式来重构秘密:
1.2 二元多项式
f(x,y)=a0,0+a1,0x+a0,1y+a1,1xy+…+at-1,t-1xt-1yt-1modp是一般二元多项式形式,其中ai,j∈GF(p),∀i,j∈[0,t-1]。如果系数满足ai,j=aj,i,那么称其为二元对称多项式;如果系数不满足上述情况,那么称其为二元非对称多项式。在二元对称多项式中,存在f(x,y)=f(y,x),所以分发者D可分配每个参与者秘密份额为f(vi,y)或f(x,vi),其中vi(1≤i≤n)为参与者公开的身份信息,任意参与者Ui和Uj(i≠j)间的会话密钥即为f(vi,vj)=f(vj,vi)。在二元非对称多项式中,分发者可分配每个参与者Ui(i=1,2,…,n)两个秘密份额f(vi,y)和f(x,vi),任意参与者可通过获得的秘密份额构造会话密钥f(vi,vj)或f(vj,vi)。
1.3 秘密共享同态性
Benaloh[20]首次引入秘密共享同态性的概念。定义秘密群为S,相应的秘密份额群为T。函数F为(t,n)秘密共享中T到S的映射函数,函数F将基于任意t个秘密份额{si1,sit,…,sit}的秘密S定义为S=FI{si1,sit,…,sit},其中任意t个秘密份额集合表示为I={si1,si2,…,sit}。

根据定义可知,Shamir门限秘密共享方案满足秘密共享(++) 同态性,即两个多项式f(x)、g(x)的秘密份额之和等于多项式(f(x)+g(x))之和的秘密份额。
2 本文方案
2.1 动 机
首先,考虑现有秘密共享方案在秘密重构阶段存在外部敌手时,虽然构造额外密钥协商机制可抵抗外部攻击,但其复杂性与参与重构者数量存在二次关系,在实际环境中方案复杂性高,系统运行效率低。其次,文献[18]提出的PSS方案有着单秘密共享的局限性;文献[16]虽然是PSS方案的多秘密共享扩展,但当存在t-1个重构者合谋攻击时,仅需要重构一个秘密,即可重构所有未重构的秘密;文献[19]通过额外构造二元多项式保证安全通道,增加了方案的复杂性。针对上述问题,本文提出一种新的基于二元非对称多项式的多秘密共享方案。
2.2 符号定义
p为大素数,GF(p)为p阶有限域。U={Uv1,Uv2,…,Uvn}是参与者集合,P={Pv1,Pv2,…,Pvn}是重构者集合,其中t≤m≤n。D为诚实的分发者,vi(1≤i≤n)是n个参与者公开的身份信息。{s1,s2,…,sk}为要共享的秘密集合。f(x,y)为二元非对称多项式,t为门限值。参与者获得的秘密份额为gvi(y)=f(vi,y)modp,构造会话密钥多项式为fvi(x)=f(x,vi)modp。任意参与者间的会话密钥为Ki,j=f(vi,vj)。
2.3 方案设计
2.3.1 秘密分发
遵循2.2节定义,方案初始化大素数p、GF(p)、n、t、{s1,s2,…,sk}的值。
Step1D选择vi(1≤i≤n),vi∈GF(p)作为每个参与者公开的身份信息,保证任意两个参与者vi≠vj。
Case1假如k Step2D构造如下二元非对称多项式: f(x,y)=s1+s2x+…+skxk-1+a1,0xk+…+at-k-1xt-1+ a0,1y+a1,1xy+…+at-k-1xt-1y+…+a0,h-1yh-1+ a1,h-1xyh-1+…+at-k-1,h-1xt-1yh-1modp= (s1+s2x+…+stxt-1)y0+(a0,1+a1,1x+…+at-k-1,1xt-1)y+ (a0,h-1+a1,h-1x+…+at-k-1,h-1xt-1)yh-1modp 其中f(x,y)中关于x项的系数{s1,s2,…,sk}是要共享的秘密集合。 Step3D计算秘密份额gvi(y)=f(vi,y)modp,会话密钥生成多项式fvi(x)=f(x,vi)modp,通过安全通道发送和给参与者Uvi(i=1,2,…,n)。 Case2假如k≥t: Step4构造如下二元非对称多项式: f(x,y)=s1+s2x+…+skxk-1+a0,1y+a1,1xy+…+ak-1,1xk-1y+ …+a0,h-1yh-1+a1,h-1xyh-1+…+ak-1,h-1xk-1yh-1modp= (s1+s2x+…+skxk-1)y0+(a0,1+a1,1x+…+ak-1,1xk-1)y+ (a0,h-1+a1,h-1x+…+ak-1,h-1xk-1)yh-1modp 其中f(x,y)中关于x项的系数{s1,s2,…,sk}是要共享的秘密集合。 Step5D计算秘密份额gvi(y)=f(vi,y)modp,会话密钥生成多项式fvi(x)=f(x,vi)modp,通过安全通道发送和给参与者Uvi(i=1,2,…,n)。 Step6计算h1=f(1,0),h2=f(2,0),…,hk-t=f(k-t,0),通过Shamir秘密共享方案分发给秘密重构者。 2.3.2 秘密重构 假设参与秘密重构的诚实重构者集合为{Pv1,Pv2,…,Pvm}。 Step1重构者Pvi结合身份信息vj和gvi(y),重构者Pvj结合身份信息vi和计算双方会话密钥Ki,j=f(vi,vj)。 Step2任意重构者Pvi分别计算gvi(0)=f(vi,0)modp,此时结合Shamir秘密共享方案,重构者Pvi随机构造t-1 阶单变量多项式wvi(x),其中gvi(0)=wvi(0)。 Step5假设重构者Pvj收到m-1个其他重构者发来的cvi,vj,Pvj解密cvi,vj得到dvi,vj并分以下两种情况进行秘密重构: Case1假如k f(x,0)=s1+s2x+skxk-1+a1,0xk+…+at-k-1,0xt-1modp= Case2假如k≥t: f(x,0)=s1+s2x+…+skxk-1modp= 其中f(x,0)中系数集合{s1,s2,…,sk}即为重构的多个秘密。 定理1本方案任意大于等于t个重构者可恢复秘密。 其中f(x,0)中系数集合{s1,s2,…,sk}即为重构的多个秘密。 3.2.1 安全模型 多秘密共享方案基本安全性包括: (1) 重构过程中子秘密交换的安全性;(2) 未恢复秘密的泄露安全性。故本文方案主要针对两种攻击:内部合谋攻击和外部攻击。 内部敌手是拥有秘密份额的合法参与者,内部合谋攻击是指内部敌手可单独攻击或者与其他内部敌手合谋攻击,与其他内部敌手合谋时可迅速获得一定量秘密份额进而重构秘密,通过合谋交换子秘密在不满足门限值情况下重构秘密。本文假设内部敌手不会恶意泄露秘密份额给外部攻击者。考虑到内部参与者窃取身份,本方案由于采用会话密钥加密信息,内部参与者想要冒充其他成员身份进行攻击必须拥有构造会话密钥的秘密份额多项式,而秘密份额多项式由安全通道分发,攻击者无法构造满足条件的秘密份额多项式发起攻击,故本方案抵抗内部参与者冒充身份攻击。 外部攻击是指外部敌手是没有获得合法秘密份额的外部参与者,通过伪装成合法参与者欺骗诚实参与者,收集到满足门限值的子秘密时即可成功重构秘密。本文假设分发者与参与者间存在安全通道,仅考虑秘密重构时的外部攻击,不考虑子秘密分发时的外部攻击。 3.2.2 安全性分析 定理2当保护的秘密数k 证明:方案构造的二元非对称多项式f(x,y)包含th个不同的系数,且x阶为t-1,y阶为h-1。秘密份额fvi(x)和gvi(y)分别是阶为t-1关于x和h-1关于y的单变量多项式,每个参与者即可通过其构造t+h个形如f(x,y)的线性独立方程。当t-1个参与者合谋攻击时,可建立(t+h)(t-1)个线性独立方程,此时合谋者通过gvi(y)计算还可得到t-1个gvi(0),因此合谋者总共可得到(t+h)(t-1)+(t-1)个方程,如果th>(t+h+1)(t-1),合谋者可恢复f(x,y)。故满足条件th>(t+h+1)(t-1)可抵抗内部合谋攻击。 当k≥t时,方案构造的二元非对称多项式f(x,y)包含kh个不同的系数,且x阶为k-1,y阶为h-1。秘密份额fvi(x)和gvi(y)分别是阶为k-1关于x和h-1关于y的单变量多项式,每个参与者即可通过其构造k+h个形如f(x,y)的线性独立方程。当t-1个参与者合谋攻击时,可建立(k+h)(t-1)个线性独立方程,此时合谋者通过gvi(y)计算还可得到t-1个gvi(0),同时由于h1=f(1,0),h2=f(2,0),…,hk-t=f(k-t,0)由Shamir秘密共享方案保护,t-1个参与者无法得到其信息,因此合谋者总共可得到(k+h)(t-1)+(t-1)个方程,满足条件kh>(k+h+1)(t-1)可抵抗内部合谋攻击。 同时不失一般性,满足条件th>(t+h+1)(t-1)下, 当k 定理3本方案抵抗外部攻击, 防止外部敌手获得秘密的信息。 证明:方案可抵抗外部攻击。假设分发者D与参与者间的通道是安全的,所以本方案只考虑秘密重构过程中的外部攻击。每个参与者获得的秘密份额fvi(x)和gvi(y)即是安全的,任意参与者间的密钥对Ki,j=f(vi,vj)由各自的秘密份额计算得出,且不同参与者对根据身份信息得到不同的Ki,j。在秘密重构过程中,所有秘密份额全部通过密钥Ki,j加密传输,假设外部敌手伪造身份信息参与秘密重构,但其缺少秘密份额而无法生成密钥对,从而无法与诚实重构者交换信息。因此,本方案可抵抗外部攻击。 文献[19]中指出Harn等[16]方案不能抵抗t-1个参与者合谋攻击,当所有参与者通过秘密重构过程恢复出首个秘密si=f(i,0)时,此时t-1个参与者已经从分发者发送的秘密份额获得了多项式f(x)=f(x,0)的t-1个因子,由于恢复的秘密si=f(i,0)也是f(x)的因子,进而参与者可计算出f(x),获得所有秘密s1=f(1,0),s2=f(2,0),…,sk=f(k,0)。本文方案可抵抗t-1个参与者内部合谋攻击,同时又具有文献[16]方案多秘密共享和秘密通道的性质。与文献[16]相同,本文方案重构阶段通信复杂度和计算复杂度都是O(m),其中m为重构者数。 Zhang等[19]构造了基于二元多项式的多秘密共享方案,但是分发者需要额外构造对称二元多项式来满足参与者安全通道的性质。相比Zhang等[19]的方案, 本文方案首先无须构建额外的二元多项式来满足生成共享密钥的条件,减少了分发者计算开销。其次,方案在具有一次多秘密保护和构建参与者安全通道的性质外,还可以抵抗内部合谋攻击和秘密重构过程中的外部攻击。本文方案无文献[16]中k 本文方案与文献[8-10]相比,同样是一次多秘密共享方案,本文方案不基于任何密码学假设,是无条件安全的。其次,在实际应用中,文献[8-10]秘密共享方案需要在参与者间加入密钥协商机制,构建安全通道。本文方案分发者所产生的秘密份额不仅可以用来产生子秘密,又可以构建参与者间共享密钥,提供参与者间安全通道,降低实际环境中方案部署的复杂性。同时,会话密钥可抵抗秘密重构时的外部攻击。会话密钥加密相比公钥加密速度更快,整个流程会话密钥一次性使用,保证安全性。现有一次多密方案都需要一定程度的公开值更新,本文方案在k 表1 一次多密方案对比 本文方案与文献[16]和文献[19]重构阶段计算复杂度都为O(m),其中m为参与者数,故只对比分发阶段计算复杂度,假设构造二元多项式时间为TD,秘密多项式计算时间为Tm。本文方案与文献[16]和文献[19]在秘密共享阶段通信复杂度都为O(m)。现有基于二元多项式多秘密共享方案对比如表2所示。 表2 二元多项式多秘密方案对比 Tompa等[21]指出秘密共享方案存在秘密份额伪造攻击,当内部欺骗者提供虚假秘密份额时,使得其他诚实重构者恢复错误秘密,这就引出了秘密共享方案的公平性和欺骗识别的问题。此后多个方案通过构造可验证属性,对参与者收到的秘密份额进行验证,进而解决分发者与欺骗者的虚假秘密欺骗攻击。近年来,基于二元多项式的欺骗识别方案[15-22]与可验证欺骗识别方案[23]被提出,更是体现出当前秘密共享方案的一个重要方向。结合本文方案存在的欺骗攻击问题,下一步针对欺骗攻击对本文多秘密共享方案进行优化。 本文基于二元非对称多项式提出一种新的多秘密共享方案,无须额外构建二元多项式即可构建参与者安全通道。与现有多秘密共享方案相比,无需额外的密钥协商机制,参与者获得的秘密份额既可以生成最终秘密多项式的秘密因子,又可生成任意参与者间共享密钥。通过安全性分析,本文方案可抵抗内部合谋攻击和重构过程中的外部攻击。考虑秘密共享方案是否具有秘密份额可验证等其他额外属性,是本文未来的研究与改进方向。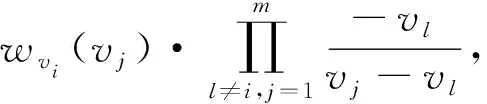
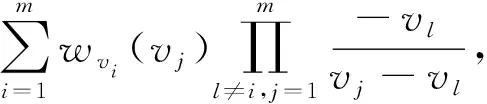

3 方案分析
3.1 正确性分析

3.2 安全模型及安全性分析
4 方案对比


5 未来工作
6 结 语

