基于因果推断肺癌患者生存时间预测方法

马真真 万亚平,2 刘 纯 周 琦

1(南华大学计算机学院 湖南 衡阳 421001) 2(中核集团高可信计算重点学科实验室 湖南 衡阳 421001)

0 引 言

肺癌作为发病率、致死率最高的恶性肿瘤,严重威胁着人类身体健康。医学资料显示:性别、吸烟等自身因素以及肺癌分期、细胞分级等与肿瘤有关的因素影响肺癌患者生存状况。如果能阐明这些病理因素与肺癌患者生存时间的因果关系,可能对评估肺癌患者的生存时间有一定的临床价值。医学上常用的统计分析方法有KaplanMeier单因素分析、COX多因素回归模型等,但回归分析会在某些情况下受限制。近年来,机器学习在医疗大数据领域取得了巨大成就,但很多情况下缺乏可解释性和稳定性。因果推断是用于解释分析的强大建模工具,可以帮助恢复数据中的因果关联,用于指导机器学习,实现可解释的稳定预测[7]。因果网络推断被认为是社会感知、流行病学因素、神经连通性和经济影响等研究的中心问题。显然,理解因果关系是实现有效控制和增强解释性的一个重要的先导步骤。

从观测数据中发现因果关系分为基于统计分析的因果推断和基于模型假设的因果推断。基于统计分析方面,文献[5]提出路径系数(Path Cofficients)的结构化定义,通过数学方法来度量因果关系。同时又提出了结构等式建模SEM(Structural Equation Modeling),目的是为了把关系规则用等式和图结合起来表示,在医学领域中应用公式如下:

y=bx+uy

(1)

式中:y表示疾病症状的程度;x表示疾病的情况;uy表示除x疾病外,其他所有可以导致y的原因。文献[12]提出了用路径分析法来确定因果关系,该方法是通过比较样本和隐含协方差矩阵,对所假设的因果关系进行统计检验,从而确定所假设的因果关系是否正确。Sun等[8]提出了利用Markov核函数在多元变量间选取最可能的假定因果方向,用来确定两个变量之间的条件依赖性。基于模型假设的因果推断方面,Shimizu等[9]提出了线性非高斯循环模型LINGAM模型,Hoyer等[10]提出了一种能处理非线性数据的加性噪声模型,Peters等[11]提出了一种基于非线性ANM的算法去解决离散数据的问题,但这些方法不能保证恢复每对变量之间的真实因果方向。后来Janzing等[3]提出了一种基于信息几何理论的因果推断算法IGCI算法。它基于输入分布和因果机制之间的独立性假设,利用信息空间中的正交性定义独立性的方法描述因果变量值之间的边缘概率分布和条件概率分布,以确定因果变量间的因果关系。另外,IGCI算法能很好地解决网络学习中存在马尔可夫等价类的问题,可以较好地控制判断率。大量实验表明,大多数高维网络数据集中,任意一个目标节点只有很少的相邻节点相连,如果一个节点表现出较强的依赖性,则该节点与目标节点可能存在因果关系。最大依赖-最小冗余(mRMR)准则[6]是因素选择方法里用来寻找因素集的重要准则。即使在高维网络下小样本数据集中,也显示出良好的可靠性和鲁棒性。

传统的机器学习回归方法构建的预测模型可能无法准确识别预测变量的全部主要因素,从而影响预测效果。为此,提出一种因果推断与深度神经网络结合的方法(MRCI-DNN)预测肺癌患者生存时间。首先利用因果推断算法构建病理因素与肺癌患者生存时间的因果网络结构图;再从因果网络图中选取影响生存时间的主要因素,建立DNN模型对生存时间进行预测。实验结果表明,基于因果推断方法筛选主要因素应用在深度神经网络预测上要优于其他选择特征方法。

1 因果方法概述

1.1 因果网络

因果网络是描述变量之间依赖关系的概率推理模型,三元变量组G=(X,E,P)常被用来表示因果网络。其中X={x1,x2,…,xn}代表有向无环图DAG中所有节点的集合,E={e(xi,xj)|xi,xj∈X}代表DAG中每两个节点间的有向边的集合,e(xi,xj)表示xi、xj间存在依赖性关系xi→xj或者xj→xi;P={P(xi|paxi)|xi,paxi∈X}是节点之间条件概率的集合,则P(xi|paxi)表示xi的父节点集paxi对xi的影响概率[4]。因果网络本质上就是联合概率分布P=(x1,x2,…,xn)的一种图表示。

定义1V结构和三角结构[15]。如图1所示,x、y、z为有向无环图DAG的3个不同节点,x、y为z的父亲节点,若x、y之间不存在直接相连的边,则该结构称为V结构。若x、y之间存在直接相连的边,则称此结构为三角结构。

(a) V结构 (b) 三角结构图1 V结构与三角结构

1.2 最大依赖-最小冗余准则

定义2最大依赖性(Max-dependenc)准则。在因素选择学习过程中,最大依赖性准则通常采用基于互信息的搜索方法来寻找与目标变量有最大依赖关系的变量集合。

最大依赖性准则具体形式为:

(2)

式中:D(y,S)表示变量y和变量S的依赖性;I(y;S)表示y与S之间的互信息大小。假设n为变量S的个数,当n=1时,式(2)等价于y与S之间的最大化互信息I(y;Si)(1≤i≤n)。若n>1,逐次向目标因素候选集增加一个变量进行增量搜索;给出k-1个变量的变量集Sk-1,则第k个变量xk须保证使得I(y;Sk-1∪xk)互信息最大化。因此有以下形式:

(3)

定义3最大依赖-最小冗余(mRMR)准则。Peng等[6]提出了一种因素选择方法,可以使用互信息,相关或距离相似性分数来选择因素。mRMR准则是理论上最佳的最大依赖性(Max-dependenc)准则的近似,其最大化所选因素和任意变量的联合分布之间的互信息。在存在其他所选因素的情况下,通过冗余来惩罚因素的依赖性,寻找与目标变量满足最大依赖的变量集合。候选因素集S与变量x的依赖程度由各个变量之间的所有互信息值的平均值定义,计算规则采取以下形式:

(4)

若采取的是每次添加一个因素进入候选因素集的选择方法,mRMR准则等价于最大依赖性准则。

1.3 基于信息几何的IGCI算法

信息几何理论提供了一个直观的途径去估算变量间的依赖关系。信息熵是对随机变量不确定性的度量。信息熵公式如下:

(5)

式中:P(xi)代表随机事件xi的概率。基于信息熵理论,Janzing等[3]提出了一种基于信息熵的因果推断方法IGCI算法。该算法在确定性关系Y=f(x)的情况下,利用信息空间中的正交性定义独立性的方法量化已知因果变量的因果强度,从而通过因果关系的不对称性来确定因果方向。该方法不须要附加噪声或后非线性模型的限制类,把二个变量之间的信息计算转化为的密度损失量,来判断变量之间的因果方向。二个变量之间的密度损失估算公式如下:

(6)

式中:H(y)和H(x)分别表示变量x、y的信息熵大小。若Cx→y<0,可以判断出x变量导致y变量;相反,若Cx→y>0,则y导致x。IGCI算法不仅可以处理确定性因果关系,而且在样本规模较小且存在低噪声的情况下,还可以获得较好的结果,对其无向图边方向推断的准确率高于其他因果推理算法。

2 基于因果推断预测流程

本文实验流程主要分为二个阶段:第一阶段基于因果推断算法分析病理因素与肺癌患者生存时间的因果关系,采用mRMR准则和IGCI算法构建完整的因果网络结构图,因果推断算法记为MRCI;在第二阶段,从因果网络结构图中选取影响患者生存时间的主要因素,利用深度神经网络(DNN)对患者生存时间进行预测。为了便于表述,本文所采用的方法记为MRCI-DNN。技术思路如图2所示。

图2 本文技术思路图

2.1 数据处理

本文收集2012年1月至2017年12月在南华大学附属南华医院就诊的695例肺癌患者病例数据作为研究对象。所选取患者病理数据均是首次确诊为肺癌,且就诊前从未进行放化疗及手术治疗。从病理数据中筛选出17种因素以及患者生存时间,数据集部分样本如表1所示。全部数据进行因子化处理,其中各节点含义用其英文名称缩写表示,非数值型因素变量赋值如表2所示。

表1 部分数据集样本

续表1

表2 非数值型因素量化

2.2 主要因素筛选

采用因果推断算法MRCI构建因果网络结构图,根据因果强度,从因果网络图中选取与患者生存时间有直接因果关系的因素作为主要因素。首先利用最大依赖-最小冗余准则(mRMR)在因素中增量搜索数据间的依赖程度,寻求与生存时间有最大依赖性的因素集,构造出有向无环图,然后结合IGCI算法对因果变量进行方向识别,最后得到完整的因果网络结构图。MRCI算法框架如图4所示。

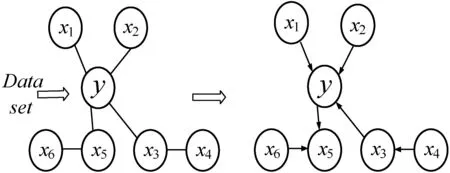
(a) 因果结构 (b) 因果网络图3 因果推断算法基本框架

步骤1给定肺癌患者数据集X={x1,x2,…,xn},分别初始化目标节点y的因素候选集S(x)={},主要因素集S(y)={}。

步骤2使用mRMR算法增量搜索与y节点依赖最大的节点xi,设置阈值m,根据依赖程度从高到低依次纳入S(x);移除大部分与目标节点y无直接因果关系的节点。

步骤3采用条件独立性测试方法移除候选节点集S(x)的非因果节点。重复步骤2-步骤3,直至所有节点迭代完。

步骤4使用IGCI算法,判定候选因素集与目标节点y之间因果方向,将影响y的因素加入S(y),即Cx→y<0。迭代所有节点,得到完整的因果网络图。因果推断MRCI算法具体描述如下:

Input: variable setX={x1,x2,…,xn};thresholdε.

Output: the casual structure ofG.

Initialization: setS(x)={},S(y)={}.

1 for eachxi∈Xdo

/*逐次寻找与y节点依赖最大的节点xm,纳入S(x)*/

employs mRMR algorithm to seek the most dependent nodesxi,

whilem≤εdo

Sm=Sm-1∪xm

thenS(x)=Sm

2 for eachxm∈S(x) do

/*利用条件独立性从S(x)选出y的因果因素*/

employs IC to remove non-causal nodes

xm∈S(x), Such that (y;xj|xm) is hold,

thenS(x)=S(x)xj

/*Repeat the above steps. */

3 for eachxm∈S(x) do

/*利用IGCI算法判别变量间因果方向*/

employs IGCI algorithm to distinguish the direction of(y,xm).

ifCx→y<0, then addxmtoS(y)

2.3 生存时间预测

第二阶段,从因果网络图中选取主要因素,利用深度神经网络(DNN)对生存时间进行预测。DNN具备多个隐藏层,网络单元间每一条链路都是一条可学习训练的因果链,使用相同网络单元,可以更好地处理复杂问题。本实验DNN预测模型以第一阶段获取的6个主要因素作为输入,其中输入层神经元个数为6,输出层神经元个数为1。通过进行大量网络深度测试和K折交叉验证,综合考虑训练精度和训练时间等因素,确定隐层为2层,隐藏层1和2神经元个数分别为64,64,每层均采用ReLU函数作为激活函数,设置Dropout以防止模型过度拟合化。深度神经网络参数设置如表3所示。此外,采用交叉验证方法把全部训练数据分为五份,随机抽取4份作为训练集,1份作为测试集,初始学习率为0.1,训练次数为500次。预测模型如图4所示。

表3 DNN参数设置

图4 预测四层DNN模型

3 实验与结果分析

主要因素筛选实验在Windows 10系统MATLAB 2017b中进行,对生存时间预测在Python 3.6.4进行。采用2012年1月至2017年12月在南华大学附属南华医院就诊的695例肺癌患者病例数据。实验第一阶段采用因果推断MRCI算法构建因果网络图如图5所示。

图5 肺癌患者各因素与生存时间因果网络图

从所构建的因果网络结构图可知,血小板与淋巴细胞比值(PLR)、中性粒细胞与淋巴细胞比值(NLR)、肺癌分期(stage)、吸烟(smoke)、肺癌分型(type)、是否接收放化疗(treat)是影响肺癌患者生存时间(livetime)的主要因素。我们还可以获悉,年龄(age)为孤立节点;肿瘤分型(type)、吸烟(smoke)、中性粒细胞数(Neu)、淋巴数(lymph)和患者性别(sex)对NLR有影响,而NLR对肿瘤大小(size)有影响;吸烟(smoke)同时影响NLR、肺癌分型(type)和肺癌分期(stage);白细胞数(WBC)除了由其包含的细胞中性粒细胞(Neu)、嗜酸性细胞(Eos)、嗜碱性细胞(Bas)、单核细胞(Mos)、淋巴数(lymph)的影响外,还受到肿瘤大小(size)、肺癌分期(stage)的影响;肺癌分型(type)、是否接收放化疗(treat)对癌胚抗原(CEA)产生影响。实验所得影响生存时间的主要因素以及因素之间的因果关系与癌症临床医学验证和现有文献分析基本一致。

第二阶段选取影响患者生存时间的主要因素S={PLR,NLR,stage,smoke,type,treat}对患者生存时间做预测。为验证本文主要因素筛选方法MRCI的有效性,分别将其于常用的特征选择方法SelectKBest以及输入全部因素预测做对比,采用SelectKBest方法挑选与患者生存时间相关性高的前六个因素T={stage,smoke,treat,WBC,PLR,NLR}。三种因素选择方法在DNN模型上性能对比如表4所示,在测试集上的预测结果分别如图6-图8所示,其中y轴表示预测的生存时间,y=x曲线表示真实生存时间。

表4 因素选择方法比较

图6 MRCI-DNN方法预测结果

图7 输入全部因素-DNN预测结果

图8 SelectKBest-DNN预测结果

由表4可知,MRCI选取主要因素预测的准确率要微优于输入全部因素预测的准确率,在误差上两者也比较接近。MRCI方法与SelectKBest方法相比,准确率上升了8.68%,估计误差分别减少了28.5%和25.2%。可以得出,MRCI方法对DNN的预测准确率有显著提升。由于SelectKBest方法选取的因素集中缺少了影响肺癌患者生存时间的主要因素,因此预测效果较差。MRCI-DNN模型的生存时间预测结果如图6所示,MRCI-DNN预测的散点图形状基本拟合y=x曲线,即在测试集上预测生存时间很大程度上与实际生存时间接近或重合。通过与另外二种方法输入预测结果的散点图比较可以看出,MRCI-DNN预测效果与输入全部因素预测效果接近,但显然优于SelectKBest方法筛选特征输入的预测效果。所以MRCI方法应用于DNN模型上具有较好的鲁棒性。从测试集中随机抽取部分样本,分别输入MRCI方法筛选的主要因素S={PLR,NLR,stage,smoke,type,treat}和输入17个全部因素进行预测,患者实际生存时间和二组因素集预测生存时间进行对比分析如表5-表6所示。

表5 实际值与主要因素预测值对比 单位:月

表6 实际值与全部因素预测值对比 单位:月

从表5-表6可以看出,将主要因素作为输入的预测值更接近实际数据,相互间误差最大为3个月,未经筛选的全部因素预测结果与实际数据误差最大为5个月。输入全部因素进行模型学习训练,实验发现采用MRCI方法筛选的主要因素权值比重大,剩余因素权重较小,更加验证了MRCI方法选择主要因素的有效性以及输入主要因素预测的准确性。这是因为因果网络推断方法寻找变量之间的因果关系时,最大化因素与生存时间之间的因果效应,最小化因素与因素之间的因果效应,利用因果约束剔除关联中的虚假关联,更准确地寻找到真正影响目标变量的主要因素。在输入全部因素进行预测时,全部因素里存在混淆变量和干扰变量,因此预测效果较MRCI-DNN预测效果较差。

由此可以看出,利用因果推断筛选主要因素的方法进行预测要优于常用的特征选择方法。常用的特征选择方法可能无法准确识别预测变量的全部主要因素,或非因素排在了主要因素前面,从而影响了预测效果。通过因果推断方法构建因果网络,可以直观地获取与预测节点有关的主要因素,且因果机制是自然属性,具有不变性,因此基于学习因果关系获得的预测模型具有一定程度的稳健性和可解释性。

4 结 语

本文针对所获肺癌患者的病理数据,提出一种基于因果推断的患者生存时间预测方法(MRCI-DNN)。采用因果推断方法筛选主要因素输入,并建立DNN网络学习模型对患者生存时间进行预测。实验结果表明,影响肺癌患者生存时间的主要因素有:吸烟、NLR、PLR、肺癌分期、接受放化疗以及肺癌分型。应用因果推断方法,对有效分析影响肺癌患者生存时间的主要因素有一定的应用价值。通过实验对比,本文采用的方法在预测效果上要优于传统机器学习方法,因此基于因果推断获得的预测模型具有一定程度的稳健性和可解释性。由于本文仅在现有数据上寻找主要因素对患者生存时间预测,数据中可能存在隐变量和一定的干扰噪声,也会影响因果分析和预测精度。因此扩大样本量,深入分析肺癌患者各因素之间的因果关系和提升预测准确度将是下一阶段的研究内容。