A bi-population immune algorithm for weapon transportation support scheduling problem with pickup and delivery on aircraft carrier deck

Fang Guo,Wei Han,Xi-chao Su,Yu-jie Liu,Rong-wei Cui

Naval Aviation University,No.188,Ermalu Road,Zhifu District,Yantai,264001,Shandong Province,China

Keywords:Carrier-based aircraft Weapon transportation support scheduling Pickup and delivery Bi-population immune algorithm

ABSTRACT The weapon transportation support scheduling problem on aircraft carrier deck is the key to restricting the sortie rate and combat capability of carrier-based aircraft.This paper studies the problem and presents a novel solution architecture.Taking the interference of the carrier-based aircraft deck layout on the weapon transportation route and precedence constraint into consideration,a mixed integer formulation is established to minimize the total objective,which is constituted of makespan,load variance and accumulative transfer time of support unit.Solution approach is developed for the model.Firstly,based on modeling the carrier aircraft parked on deck as convex obstacles,the path library of weapon transportation is constructed through visibility graph and Warshall-Floyd methods.We then propose a bi-population immune algorithm in which a population-based forward/backward scheduling technique,local search schemes and a chaotic catastrophe operator are embedded.Besides,the randomkey solution representation and serial scheduling generation scheme are adopted to conveniently obtain a better solution.The Taguchi method is additionally employed to determine key parameters of the algorithm.Finally,on a set of generated realistic instances,we demonstrate that the proposed algorithm outperforms all compared algorithms designed for similar optimization problems and can significantly improve the efficiency,and that the established model and the bi-population immune algorithm can effectively respond to the weapon support requirements of carrier-based aircraft under different sortie missions.

1.Introduction

The aircraft carrier is a floating air base capable of moving anywhere at a speed of about 700 miles per day,thus is of incomparable significance for maintaining maritime security and interests.The carrier-based aircraft it carries is sortied and recovered in a cyclic mode to perform different missions,in which weapons are the embodiment of the power of carrier aircraft and the main demand for tasks.After recovery of a group of aircraft,a series of flight deck operations need to be completed according to the technological process,including dispatching from one spot to another,inspection of each part,fueling,weapon mounting,nitrogen charging,oxygen filling,alignment of inertial navigation system,launching at the catapult and so forth[1].These operations can be classified into three stages: dispatch path planning,maintenance and service support scheduling,and sortie scheduling.In terms of scope,weapon transportation support operation runs through the entire maintenance and service support process,and its purpose is to transport and mount weapons during that process.Due to its long support period,the efficiency of weapon transportation support operation is one of the key bottlenecks restricting the sortie rate of carrier-based aircraft.

Specifically,weapon transportation support scheduling problem(WTSSP) involves transporting various types of weapons stored in the weapon storage center (WSC) on carrier deck to the weapon mounting points mainly located under the aircraft wing and then mounting the weapon.When the aircraft carrier formation encounters a change in combat missions,such as switching from a sea assault mission to an air combat mission,it is necessary to simultaneously replace the weapons mounted on the planned aircraft.This will lead to the problem studied in this paper.The WTSSP with pickup and delivery(WTSSPPD) requires that while some types of weapons are mounted,other types of weapons already mounted should be unmounted and delivered back to the WSC.This situation once occurred during the Battle of Midway in World War II and exerted a severe impact on the combat capability of the aircraft carrier formation,which motivates us to study the WTSSPPD.

Essentially,WTSSPPD has a lot in common with the vehicle routing problem (VRP) with simultaneous pickup and delivery(VRPSPD).In the VRPSPD,customers have a delivery demand or a pickup demand,but at least one customer simultaneously has pickup and delivery demand.Since extending the VRP,the VRPSPD is NP-hard and consists of two sub-problems.The first one is to assign each demand of the customer to a vehicle,and the second is to sequence the assigned demands on all vehicles.However,compared with the VRPSPD,stricter constraints are imposed on the WTSSPPD.Firstly,precedence constraints exist when a weapon mounting point as a customer has both a pickup and a delivery demand.In this case,it must first complete the pickup operation before delivery.Secondly,a handling vehicle for weapon cannot carry different types of weapons at the same time.As a result,each weapon mounting point is not limited to be visited by exactly one handling vehicle in the WTSSPPD.Moreover,there are several handling vehicles for weapons with different capacity on carrier deck.Therefore,it is imperative to make a time-saving and robust schedule which satisfy the constraints of space,resource,timing and personnel as the efficiency of weapon transportation support operation is the bottleneck of improving the sortie rate and operational management level of an aircraft carrier.

This paper focuses on the WTSSPPD,and the contributions are predominantly in two aspects.(1) We construct a comprehensive and realistic model for the WTSSPPD with the objective of minimizing the makespan,load variance and accumulative transfer time of support unit.In the model,the carrier aircraft parked on deck is regarded as convex obstacles and the path library of the handling vehicles for weapons is established based on the visibility graph and Warshall-floyd method.(2)A bi-population immune algorithm(BPIA)is proposed for solving the WTSSPPD.It expands the iterative forward/backward scheduling technique into a bi-population structure for the precedence constraints in the problem,and introduces four local search schemes and a chaotic catastrophe operator according to the characteristics of the problem.

The reminder of this paper is organized as follow.Section 2 presents a literature review of related work.In Section 3,a problem statement for the WTSSPPD is given.Section 4 lays out the construction of path library of weapon transportation.A mathematical model aiming at minimizing the makespan,load variance and accumulative transfer time of support unit is formulated in Section 5.In Section 6,the proposed BPIA is described in detail.Section 7 is devoted to present and discuss the experimental results.The last Section concludes the paper.

2.Literature review

To the best of our knowledge,there is no literature on WTSSP,let alone WTSSPPD.In view of the fact that WTSSPPD is an important part of flight deck operations,and the characteristics of WTSSPPD share many common points with VRPSPD,we investigate the research progress of scheduling of flight deck operations and VRPSPD in this section.

2.1.Scheduling of flight deck operations

Flight deck operations presents a more complex and narrower environment compared with the ground operations on the airport.Therefore,time-critical scheduling and planning must be done to fulfill mission requirements and ensure the safety of crew and equipment[2].For the dispatch path planning problem,Wang et al.studied the coordinated taxiing planning for multiple aircraft on flight deck[3]and made a comprehensive investigation on research progress for the carrier aircraft's dispatch path planning on the deck [4].For the scheduling problem of maintenance and service support,Cui et al.[5,6]and Su et al.[7]investigated the flight deck operations scheduling problem and resource configuration optimization problem at preflight preparation stage.Yuan et al.[8]and Su et al.[1,9]introduced dynamic factors into the deck support operations scheduling problem,and studied robust scheduling problems,proactive and reactive scheduling problems for it.These researches all attribute the flight deck operations to the resourceconstrained project scheduling problem,and good results are achieved under the set conditions.However,in these studies,the weapon support operation is only regarded as a process,and it only includes the operation of mounting weapon,and does not include the path planning problem of transporting the weapon from the WSC to the weapon mounting point.Besides,Luan et al.[10]studied the part transportation of aircraft carrier with stochastic demand and transportation time and designed a control strategy to realize the timely and stable supply of parts for carrier aircraft repair.As far as the sortie scheduling is concerned,Liu et al.[11]built a hybrid flexible flow shop scheduling model for sortie scheduling of carrier aircrafts from the perspective of the whole scheduling and dispatch process on deck,and proposed a doublelayer genetic algorithm.Based on a similar model,a Q-learning method is also designed for the sortie scheduling problem [12].

2.2.Significant progress in VRPSPD

Over the past few decades,the VRPSPD has evolved into a rich and active research field.As for its related mathematical formulations,two types of typical models are mainly established.The vehicle-flow model only specifies the route of the vehicle,while the commodity-flow model specifies the number of goods picked up and delivered on each arc[13].To address the challenge of VRPSPD,several exact algorithms [14—16]and heuristic methods [17—19]have been developed for small-scale VRPSPD.As the number of customers involved increases,meta-heuristic algorithms are introduced to solve VRPSPD.Bianchessi and Righini[20]described a variable neighborhood scheme combining several heuristics with local search procedure.Ai and Kachitvichyanukul[21]developed a particle swarm optimization,in which the random keys is adopted to represent the solution and a priority of matrix for vehicles is designed to serve the customers.Vidal et al.[22]proposed several effective procedures to intensify and diversify their designed genetic algorithm solutions.Integrating an array of local search schemes,Gajpal and Abad[23]improved an ant colony system for VRPSPD.In recent years,many variants of VRPSPD have been studied [13],such as the VRPSPD with time windows,the heterogeneous VRPSPD,the multi-depot VRPSPD,the green VRPSPD,the stochastic VRPSPD.

Based on the above discussions,we believe that the conclusions are possibly twofold.On the one hand,the study of WTSSPPD,which is a new research question,is to complement and perfect flight deck operations to make it more suitable for practical applications.On the other hand,the WTSSPPD studied in this paper is a large-scale problem with stricter constraints compared with VRPSPD.Consequently,it is difficult to obtain satisfactory results with exact algorithms and heuristic rules.An ideal method may be to integrate meta-heuristic algorithms and effective local search schemes.

3.Description of the problem

WTSSPPD can be classified as a variant of VRPSPD.The deck layout of the USS Gerald R.Ford aircraft carrier is illustrated in Fig.1,the WSC can be regarded as the only depot responsible for storingKatypes of weapons,and is equipped withKv types of heterogeneous handling vehicles for weapon,each type is composed ofnkhandling vehicles.A handling vehicle and several support personnel form a support unit in charge of the transportation and support operation (mounting or unmounting) of weapons.A support unit can only carry the same type of weapons in one batch.Generally,there are mainly two types of support units on carrier deck:human-powered support units and electric ones.

The weapon mounting point mainly located under the aircraft wing can be considered as a customer having a delivery demand or a pickup demand,or having both a delivery demand and a pickup demand.After the weapon is carried below the mounting point,it is lifted and mounted by the support personnel in the manual support unit,while the electric support unit completes these support activities in mechanized way.The situation is similar when unmounting the weapon.It is worth noting that there exists strict precedence constraint in a weapon mounting point if it has both a pickup and a delivery demand.For such weapon mounting point,the unmounting operation must be completed first.

For WTSSPPD,when a weapon support mission starts,support units will departure from the WSC.There are two ways to complete support operation for a support unit.First,the support unit load the weapons at WSC and deliver them to customers to mount weapons.After all the loaded weapons on the handling vehicle are mounted,the unit can choose returning to the WSC to reload weapons or going directly to unmount weapons which need to be picked up and transport them back to the WSC.In the second way,the support unit goes directly to customers that first have a pickup demand to unmount the weapons and deliver them back to the WSC.Fig.2 describes these two weapon support ways.

In summary,different from the vehicle in VRPSPD,a support unit in WTSSPPD can only transport the same type of weapons in one batch.And the capacity and support time,as well as the travel speed are different for each type of support unit to support different types of weapons.Besides,the support route of support unit is restricted by the obstacles(convex hull of aircraft,the island and the border) on carrier deck and is not a fixed route,thus it needs to be planned according to the layout of the carrier-based aircraft.

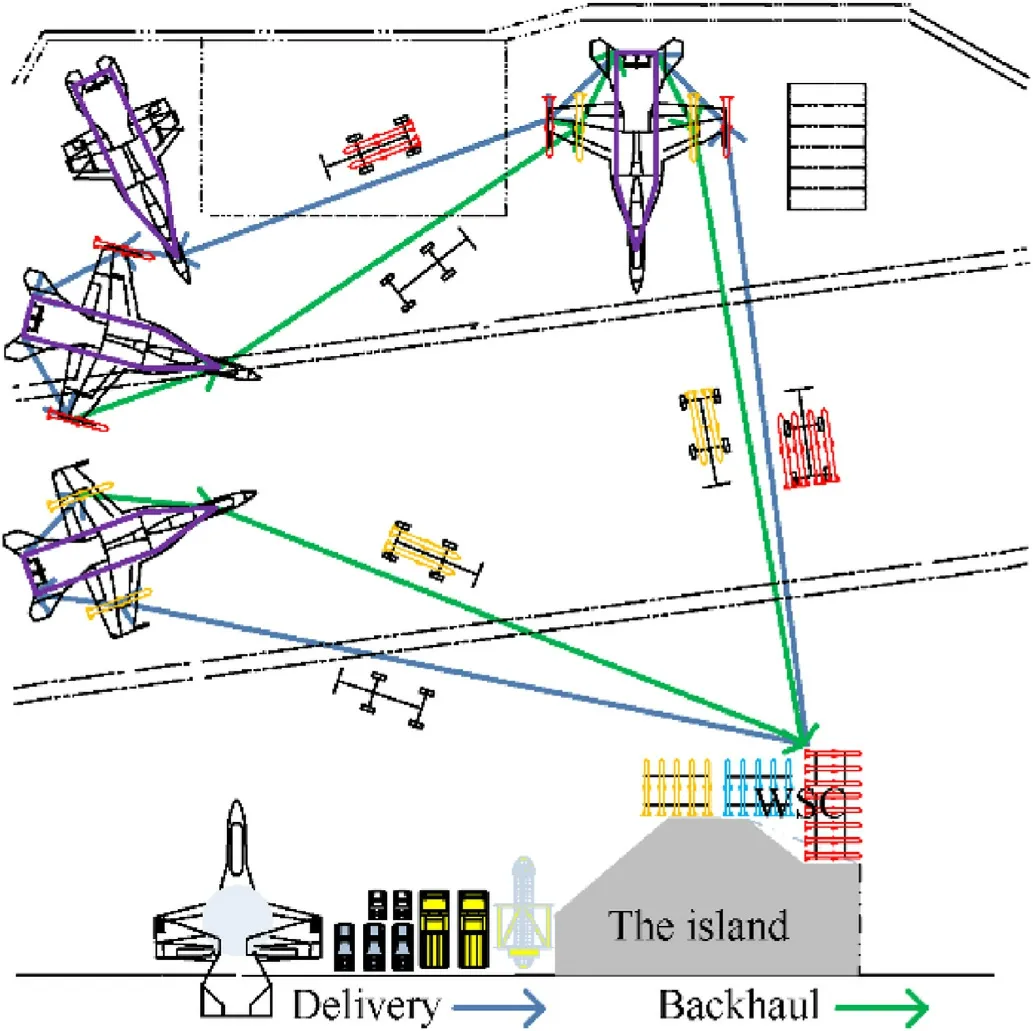
Fig.2.Two weapon support ways of support unit.

4.Path library construction of weapon transportation

Based on the shape and structure of the carrier-based aircraft,its convex hull model,depicted in Fig.3,is established.The weapon mounting points of carrier-based aircraft are numbered from right to left of the aircraft.Due to the low height below the convex hull of the carrier-based aircraft,the support unit can only travel around the convex hull shown in Fig.3,thus the carrier-based aircraft parked on deck becomes an obstacle to the transportation of the weapons.Consequently,the travel route of the support unit is not always a straight line.It is determined by the deck layout status of the carrier-based aircraft.

In order to describe the position (coordinates and azimuth angle)of the carrier aircraft at any time on deck,the position model of the aircraft shown in Fig.4 is constructed.Taking the midpoint of the two engine tail nozzles as the coordinate reference point,the angle between the vector line of the front and the midpoint pointing to the nose and the x-axis of the deck is regarded as the azimuth angle of the carrier aircraft.

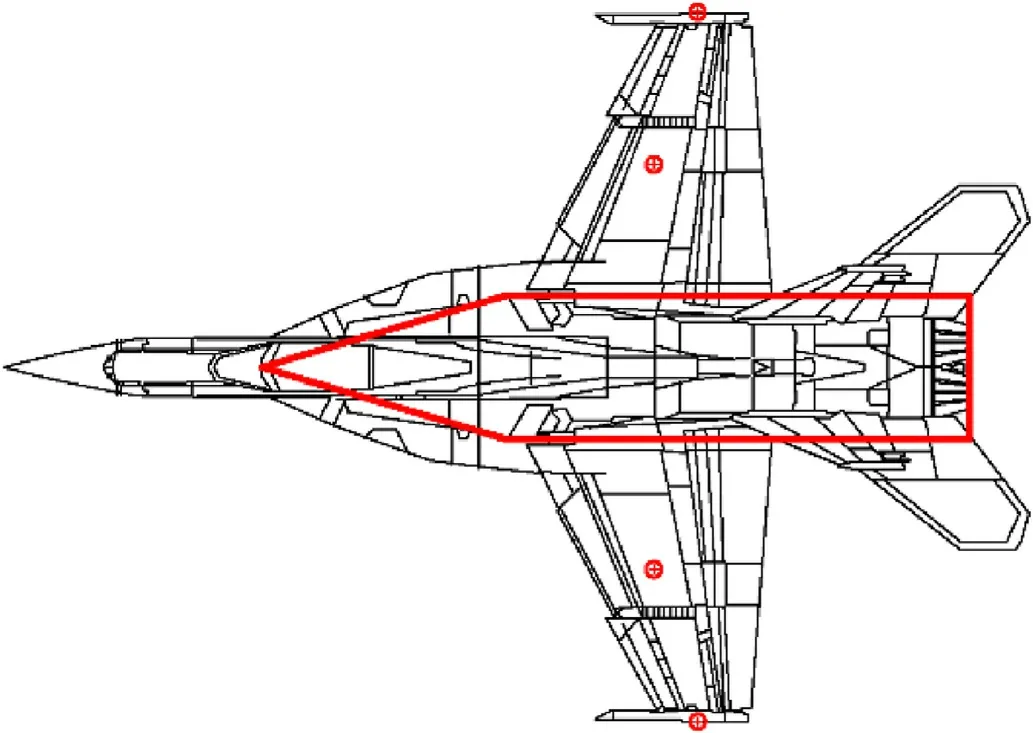
Fig.3.Convex hull model of carrier aircraft.

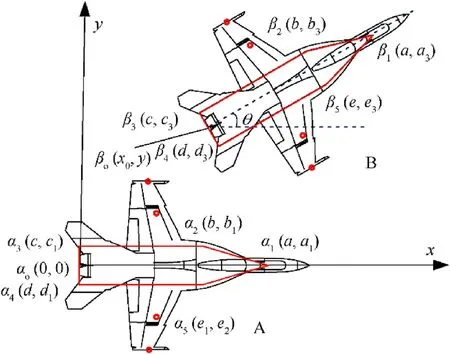
Fig.4.The position model of the carrier aircraft.

Since the dimensions of carrier aircraft are known when modeling,the coordinates of each vertex of the convex hull,as well as the coordinates of the weapon mounting points,can be described when the reference point is at the origin of the coordinates.In Fig.4,Arepresents the standard position of the carrier aircraft at the origin of the coordinates.Once the coordinates of the reference point β0(x0，y0）and azimuth angle θ of the carrier-based aircraft are known,the positionBcan be obtained by rotating and translating the standard positionA.After performing the above operations on a certain point α(x，y）on the carrier aircraft in the positionA,the coordinates of the corresponding point β(x′，y′）in the positionBcan be obtained by Eq.(1),in which T represents the transformation matrix of position conversion fromAtoB.Therefore,the coordinates of the vertices of the convex hull and the weapon mounting points of the carrier aircraft in the layout status depicted in Fig.1 can be obtained in this way from the corresponding coordinates in the standard positionA.

With good mobility,the handling vehicle for weapon can travel along any broken line on the deck,so the visibility graph[24]which is often used for path planning and real-time collision avoidance of unmanned aircraft is adopted to solve the optimal support route.Specifically,it is necessary to construct a convex hull model of all obstacles on the deck,and connect the visible vertices to form a visibility graph,and then the Warshall-Floyd method can be used to solve the shortest route between two points required.The method for constructing the weapon transportation path based on visibility graph is carried out in the following steps:

Step 1:Based on the layout status of the carrier aircraft on deck and weapon support mission of each aircraft,constructing the vertices set of convex hulls of obstacle and the set of weapon mounting points.

Step 2:Integrating all convex hull vertices,weapon mounting points and WSC form a vertex setV,and then connecting any two points inV.For the barrier-free visible line,calculating the Euclidean distance of the two points,and the distance between the two points with obstacles is defined as infinity.Finally,constructing the distance matrix W among all vertices.

Step 3:Construct a visible undirected graphG=(V，E）,whereEis the set of barrier-free visible line.

Step 4:Based on Warshall-Floyd method,calculating the shortest distance and corresponding route between two vertices required.Further,the path library among all vertices can be calculated.

5.Mathematical formulation

5.1.Problem assumptions

Based on the previous description,we make the following assumptions:

(1) The transfer time of the support unit is only related to the distance and type of support unit,and has nothing to do with the number of weapons it transports and the fatigue of support personnel.

(2) There is sufficient parking space on deck,and no space interference exists when the carrier-based aircraft wing is unfolded for mounting or unmounting weapons.

(3) The WSC stores enough weapons and can be supplemented in real time,thus the number of weapons can meet the demand of the aircraft at any time.

(4) The collision between handling vehicles for weapon is not considered,because it is easy for these handling vehicles with good mobility to avoid that situation.

(5) When customers assigned to the support unit is determined,the support will support as many customers as possible in each batch.

5.2.Notation

The relevant notations and decision variables for modeling WTSSPPD are provided in Table 1.

Table 1 The relevant notations and decision variables for modeling WTSSPPD.

5.3.The constraints of the WTSSPPD

We model the WTSSPPD as a mixed integer formulation,and the constraints can be described as follows:

Constraint 1: ∀(i，j），(e，g）∊OA，∀b∊Bkl，∀m∊Ka，∀k∊Kv，∀l∊Lvk,a support unit can only transport the same type of weapons in one support batch.

Constraint 2:∀(i，j）∊OA，∀b∊Bkl，∀m∊Ka，∀k∊Kv，∀l∊Lvk,the number of weapons a support unit transport cannot exceed its maximal capacity.

Constraint 3:∀(i，j）∊OA，∀b∊Bkl，∀m∊Ka，∀k∊Kv，∀l∊Lvk,the duration of operationOijis determined by the weapon type it needs to be mounted or unmounted and the category of the support unit.

Constraint 5: ∀(i，j）∊OA,the relation between the starting and ending time of any operation reads as

Constraint 6: ∀(i，j），(e，g）∊OA，∀b∊Bkl，∀m∊Ka，∀k∊Kv，∀l∊Lvk,the operation timing constraint in the same support batch for any support unit holds that.Note that

This constraint ensures that if operationOijis supported prior to operationOegby the same support unit in the same batch,the start time of operationOegis enforced to be larger than the completion time of operationOij.Bis a large enough positive number and it ensures that the inequality always holds even when.Here,considering the duration of weapon transportation support operations,B=10∧3is large enough.

Constraint 7: ∀(i，j），(e，g）∊OA，∀b∊Bkl，∀m∊Ka，∀k∊Kv，∀l∊Lvk,the operation timing constraint in two adjacent support batches for any support unit yields

where the value ofBis similar to the above constraint,andTransijegkis the transfer time between two operations in two consecutive support batches of the same support unit,

Constraint 8: ∀(i，j）∊OA,any operationOijis assigned to a support unit.

5.4.The objectives of the WTSSPPD

In order to increase the efficiency of weapon transportation support scheduling and ensure the safety of personnel and equipment on deck,the objective function of the WTSSPPD is set to minimize the makespan,load variance and accumulative transfer time of support unit.

(1) Minimizing the makespan

In order to ensure the completion of weapon transportation support operations as soon as possible to reduce the impact on subsequent support operations,the first optimization goal is set to minimize the makespan.

(2) Minimizing the load variance of support unit

That the support unit is in good working condition is the prerequisite to continuously and efficiently perform weapon transportation support operations.If the support operations of some support units are intensive and heavy,and the other support units are relatively idle,this kind of load imbalance among support units is not conducive to maintaining a good long-term operation status of support units.Therefore,load variance of support unit is employed as an optimization indicator to measure the load balance.

where the load of thel-thsupport unit with categoryk(k∊Kv，l∊Lvk)TBkl,as shown in Eq.(14),can be expressed as the weighted sum of operation time (mounting or unmounting weapons),transfer time and loading or unloading time of support unit.In Eq.(14),Tijegk,defined in Eq.(15),is the transfer time of a support unit between two support batch.Cij00kandC00egkrepresent the time consumed by thek-thcategory support unit from operationOijto WSC and the time from WSC to operationOeg,respectively.

(3) Minimizing the accumulative transfer time of support unit

Due to the various hazards on the deck,the frequent transfer of support personnel on the deck will not only increase a certain safety risk,but also may result in certain interference to the transfer of carrier-based aircraft and equipment on the deck.Thus,the third optimization goal of the WTSSPPD is set to minimize the cumulative transfer time of support unit.

whereTijegkis the same as that in Eq.(14).

In this paper,we combine three objectives in lexicographic order as Eq.(17)indicates,wherewi∊(0，1），Σwi=1，i∊｛1，2，3}.The Analytic Hierarchy Process(AHP)approach is adopted in evaluating a weight index for each of objective.

5.5.Determination of the weight of objective based on AHP approach

AHP is a technique developed for solving complex problems concerning multiple criteria [25].The adoption of the AHP technique is its capability to accommodate subjective factors in an organized manner [26].For this paper,three sub objectives are firstly assessed relative to each other,which then creates a hierarchy of assessments with two levels that ultimately generates numerical weights for each sub objective.

Specifically,the pairwise comparisons of three sub objectives are undertaken according to the relative importance of them on WTSSPPD,and the value results of these comparison are compiled into a pairwise comparison matrix PC as Eq.(18) illustrates.Subsequently,we calculate the weight vector w=[0.705，0.084，0.211]with the consistency ratiocr=0.056<0.100.Further details can be found in Ref.[27].

6.The proposed BPIA algorithm

6.1.The immune algorithm

The biological immune system responds to the invading antigen by generating antibodies,thereby eliminating the antigen [28].Mimicking the natural immune system,immune algorithm provides an ideal tool for combinatorial optimization problems [29].

To be specific,in immune algorithm,the objective function of the problem to be optimized is regarded as the antigen,whereas antibodies are the candidate solutions.It iteratively performs antigen recognition,antibody affinity evaluation and immunization until the termination condition is met.The antigen recognition is usually accomplished by generating a random initial population of antibodies.Antibody affinity evaluation is to calculate the affinity of each feasible solution in the antibody population.The immunization is executed on the basis of immune operator which mainly consists of clone selection and expansion,affinity maturation and receptor editing.By these operations,immune algorithm to some extent inhibits individual's degradation and fluctuation in the late evolution compared with stochastic optimization algorithm that adopts completely random optimization process [30].

The utmost important characteristics of immune algorithm are strong global optimization capability,robustness,as well as the maintenance mechanism of population diversity.And it has achieved promising results in the VRP[31]and the dynamic scheduling problem in production domain [32,33].

6.2.The proposed BPIA

This paper improves immune algorithm and proposes a BPIA for the WTSSPPD.For the sake of existing the precedence constraints in the WTSSPPD,it can also be regarded as a resource-constrained project scheduling problem (RCPSP) when considering the weapons required as resources.Hence,as a well-known local search technique for RCPSP meta-heuristics,the iterative forward/backward scheduling technique[34]is integrated into the immune algorithm to form a BPIA framework.To increase the local search capability of BPIA,four other local search schemes adapted to the WTSSPPD are also introduced in the BPIA.Besides,a chaotic catastrophe operator enlightened by the scout's mode of artificial bee colony algorithm is incorporated into the BPIA to avoid getting stuck in a local optimal solution and maintain diversity of the population.What is more,for better exploration and to ensure the diversity,a crossover operator is carried out besides a mutation operator in affinity maturation phase.Finally,we select antibodies to enter the other population based on antibody affinity and concentration criteria.

Through BPIA computation,the antibody with highest affinity will finally be selected as the solution to the WTSSPPD after implementing a predetermined number of schedule generations.Fig.5 shows the flowchart of the proposed BPIA and the detailed steps are described as follows.Note that we describe the algorithm optimization process at the antibody level,but the actual execution process is based on the antibody population.

6.2.1.Antigen recognition

Antigen recognition is to model WTSSPPD as illustrated in Section 4,and we define the affinity function as the reciprocal of the overall objective function.Based on Eq.(17),the affinity of an antibody is

6.2.2.Construct an initial population of left-justified schedule

We only initialize the population of left-justified schedule(PopL)with population sizePS.The initialization of each antibody refers to the representation of a schedule which can be seen as encoding a schedule.Up to now,activity-list representation and random-key representation are the most widespread solution representation methods[35].A priority structure between activities(operations)is necessary for solution representation and is embedded in both representations.In order to facilitate the execution of various operators in our proposed algorithm,the random-key representation is utilized in our procedure.

Usually,the random-key representation adopts a vector x∊Rnsuch thatxp∊x indicates the priority of operationp.Adapting to the characteristics of the WTSSPPD,we use a matrix to encode the antibody with size (na，nw，2）as Eq.(20) shows.

wherenadenotes the number of carrier aircraft to be supported,nwindicates the number of weapon mounting point of each aircraft,andcorrespond to operationand operation,respectively.And，∀Oij∊OAis a real number,the integer part represents the support unit for which operationOijis to be supported,and the fractional part indicates the priority of the operation.

In addition,we define a state matrix S with the same shape as A to identify whether an operation needs to be supported in a certain weapon transportation support mission.Note that the state matrix is a parameter that needs to be set for different support missions.

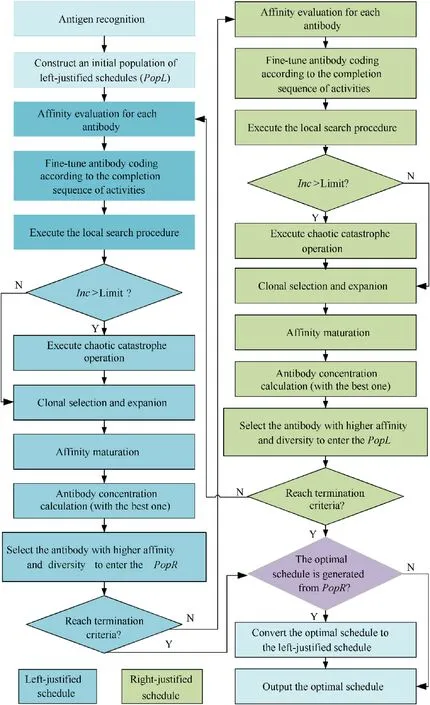
Fig.5.Flowchart of BPIA.

6.2.3.Affinity evaluation for each antibody

For antibody affinity evaluation,we first decode the antibody to generate a schedule,and then calculate the objective function and affinity.

A schedule generation scheme (SGS) is indispensable for decoding an antibody into a schedule.Alternatively,there exist two SGSs:a serial SGS and a parallel SGS.Kolisch [36]showed that the parallel SGS cannot always reach the optimal solution compared with the serial SGS.Hence,we adopt the serial SGS.The serial SGS constructs an active schedule by scheduling each operation one at a time within the precedence and resource constraints [35].And there are three disjoint task sets at each stage.The scheduled setSgincludes those tasks that have been scheduled with a start time and whose required resources are allocated.The decision setDgincludes those tasks that have not yet been scheduled and meets.The inactive tasks setUgmeetsDg.

We calculate the Hadamard product H of antibody encoding matrix A and state matrix S for antibody gene decoding,which is equivalent to setting the corresponding real numbers∀Oij∊OAin matrix A to 0 for operationsOij∊OAthat do not require to be supported.That is,

For each antibody withNoperations,the serial SGS consists ofNstages.In each stage,the serial SGS selects an operationOij∊Dgbased on the predetermined priority sequence.We may define that the smaller the fractional part ofhij，(∀hij≠0）,the higher the priority of the operationOijin left-justified schedule and the opposite is true in right-justified schedule.Then the operation is assigned to a support unit and the starting time of it is scheduled as soon as possible.Following the progress of the scheduling stage,the serial SGS gradually expands the schedule to complete the entire decoding.

However,performing the serial SGS once for an antibody is not enough to get a schedule that can be directly applied to the WTSSPD.Because it is difficult for a support unit to determine the number of weapons needing to be loaded in next support batch after completing a batch of support and returning to WSC.Consequently,we perform the serial SGS twice,and we fine-tune the antibody coding exploiting the operation completion sequence of each support unit after the first serial SGS,we additionally assume that the support unit will load weapons with the maximal capacity in the support batch of mounting in the first serial SGS.We take the PopL as an example to build a left-justified schedule,and the establishment of the right-justified schedule is similar.Note that the mounting operation (and duration) in right-justified schedule corresponds to the unmounting operation (and duration) in leftjustified schedule,the same as the loading and unloading process at WSC.

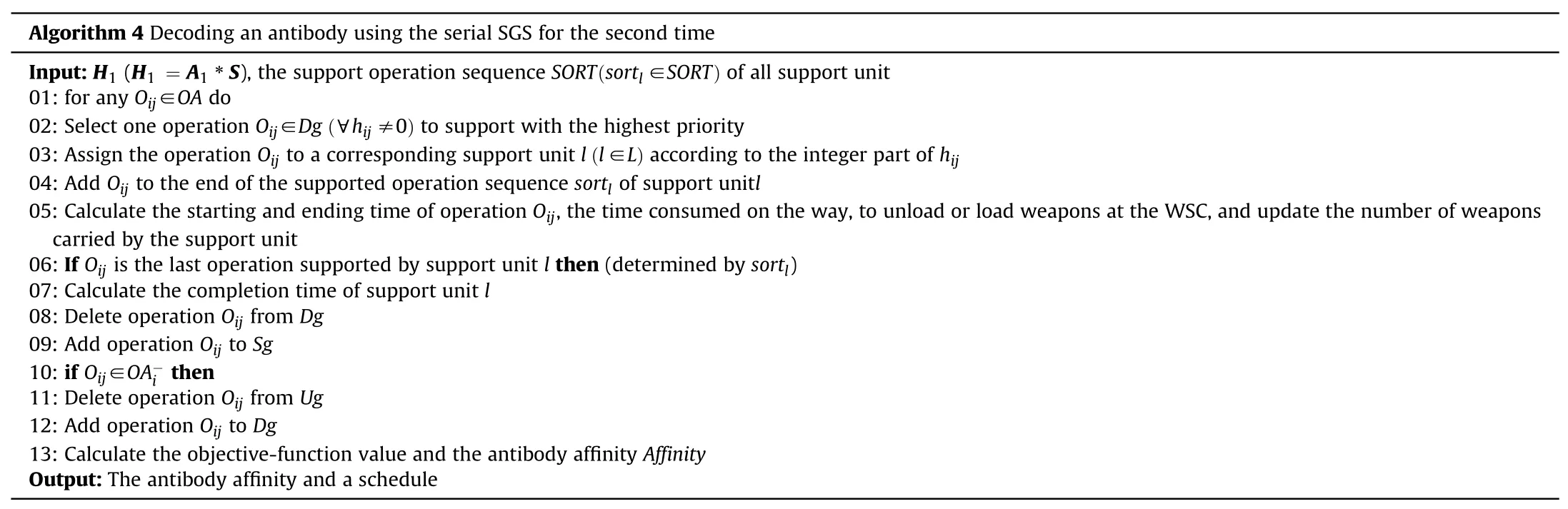
The details of these procedures are shown in Algorithm 1 to 4.

Algorithm2,contained in Algorithm 1,defines an insertable markInsertlfor each support unit to indicate the position where the newly selected operation might be able to be inserted.Insertlis a binary vector,with 1 indicating the position might be inserted by an operation and 0 indicating the position cannot.Fig.6 illustrates the detail.The condition that the newly selected operation can be inserted is that to complete the inserted operation does not affect the operations in scheduled sequence.The reason why the mark vectorInsertlworks is that the corresponding operationOijof 1 inInsertlmeets,and the support unit travels the shortest route between two weapon mounting points.Taking the first attemptin Fig.6 as an example,the starting time ofO13(O13=）can be calculated as Eq.(23) based on the constraints of the WTSSPPD.The maximum function makes it possible for the support unit to have waiting time between two operations.During the waiting time,the support unit may complete the newly selected operation without affecting the completion of subsequent operations in the support operation sequencesortl.

Fig.6.The insertion attempt process of newly selected operation.

Before performing the second serial SGS,we fine-tune the antibody coding according to the practical support operation sequence.Algorithm 3 illustrates the detailed procedures.

Then the second serial SGS,as shown is Algorithm 4,is carried out to get a schedule that can be directly applied to the WTSSPD.The most important difference between Algorithm 4 and Algorithm 1 is that the Algorithm 2 is not required,and the second is that we have to calculate the starting and ending time of specific activities in Algorithm 4.

6.2.4.Fine-tuning the antibody coding

The procedures to fine-tune the antibody coding are illustrated in Algorithm 3.The reason for these operations is that the operation support order after performing the insertion attempt scheme in Algorithm 1 is not necessarily consistent with the operation support sequence corresponding to the priority of the antibody coding.

6.2.5.Executing the local search schemes

In order to improve the local search capability of the proposed algorithm,we introduce four other local search schemes into BPIA in addition to the forward/backward scheduling technique.The first is to randomly exchange support sequence of two operations in a stochastic support unit.The second is the random exchange of an operation between two support units.The third is to select an operation from one support unit and to insert it into another support unit.When the number of population iterations is less than 20,we select the operation from the support unit with the longest completion time and insert it to the support unit with the smallest completion time.Then we randomly select two support units,and choose one operation from the support unit with the longer completion time and insert it into the support unit with the smaller completion time.The fourth local search scheme is to randomly exchange two adjacent operations between two support units.

Fig.7.A cyclic mutation example of an antibody.

6.2.6.Performing chaotic catastrophe operator

A chaotic catastrophe operator is incorporated into the BPIA with the purpose of avoiding trapping in the local optimums and enhancing population diversity.The proposed algorithm will perform the chaotic catastrophe operator if the optimal value of the antibody population is not updated after a certain number of iterations.In this operator,we define a series of operations called cyclic mutation.The three steps necessary to perform the chaotic catastrophe operator are described as following steps:

Step 1: Sort the antibodies of the population with the descending order of their affinities.

Step 2: Retain the top 10% antibodies with highest affinities directly into the new population

Step 3: The remaining 90% antibodies are generated from the last 90% antibodies using a cyclic mutation operator which is shown in Algorithm 5 and Fig.7.

6.2.7.Clonal selection and expansion

We select thencnumber of antibodies in the population with highest affinity.Thene(>nc）number of antibodies are generated from the selected antibodies using the two-tournament selection where two antibodies from the selectedncantibodies are chosen stochastically.

6.2.8.Affinity maturation

For better exploration and to ensure the diversity,a two-point crossover operator is carried out besides a mutation operator in this stage.The two operators will be performed for each clone where a higher objective-function value results in a higher performing probability[33].That of thei-thclone is calculated by Eq.(24)wherefiis the objective-function value (reciprocal of affinity)of thei-thclone,andfmax，fminis the maximum and minimum of all the clone objective-function value,respectively.Note that the crossover operator is performed first.And the antibodies on which the two operators are performed will be added to the antibody population.This guarantees that there are basically no two identical antibodies in the expanded antibody population,which further ensures the diversity of the population.

For the two-point crossover operator,we randomly select a clone different from thei-thclone,and form the two parents together with thei-thclone.Subsequently,we flatten the selected parental antibody genes,and randomly select two intersection points before and after half the length of the antibody genes,then the genes between the two points of thei-thclone is substituted with these of another clone.

The mutation operator exploited in this stage is the inverse mutation as Algorithm 6 shows.

6.2.9.Antibody concentration calculation

To reduce complexity of the algorithm,only the concentration of the antibody with the highest affinity is calculated.Specifically,we calculate the Euclidean distance of effective coding between it and other antibodies in the expanded population,and we define the concentration of the antibody with the highest affinity as the reciprocal of that distance.Thus,the concentration calculation formula is Eq.(25),where Hbestis the Hadamard product of the antibody coding with highest affinity and Hkis the Hadamard product of any antibody coding.

6.2.10.Survival selection

To effectively maintain the diversity of antibody genes in population,we select theratio%PSnumber of antibodies in the expanded population with higher affinities and (1-ratio%）PSnumber of antibodies with lower concentration,to enterPopR.

6.2.11.Computational complexity analysis

The path library construction of weapon transportation can be done offline.In addition to the random initialization complexity ofO(nanw）,the computational complexity of the proposed BPIA is mainly reflected in decoding and optimization operators.In terms of antibody,thePopLandPopRare consistent in computational complexity.The serial SGS has the complexity ofO(NnanwNs）,whereNsis the number of support unit.In the stage of fine-tuning the antibody coding,the complexity isO(Nnanw）in the worst case.The complexities of local search,chaotic catastrophe operator,affinity maturation and concentration calculation areO(N2）,O(nanw）,O(N2）andO(nanw）,respectively.Hence,the overall complexity of the proposed algorithm isO(NnanwNsNsch）,whereNschis the maximum number of schedule generation.

7.Computational results

7.1.Simulation case generation

In order to evaluate the performance of the established model and the proposed BPIA for the TSSPPD,a set of realistic instances are generated based on the USS Gerald R.Ford aircraft carrier.Three typical mission cases of weapon transportation support cases are introduced.

Mission Case 1: 14 aircraft,parking at A1 to A14 (shown in Fig.1),are assigned for weapon support operations for Type II and Type III weapons,at the same time 8 aircraft,parking at A1 to A8,have been mounted with 4 weapons with Type I which must first be unmounted and delivered back to the WSC.This is a small-size WTSSPPD.

Mission Case 2:20 aircraft,parking at A1 to A20,are assigned for weapon support operations for Type II and Type III weapons,at the same time 10 aircraft,parking at A1 to A10,have been mounted with 4 weapons with Type I which must first be unmounted and delivered back to the WSC.This is a medium-size WTSSPPD.

Mission Case 3: 26 aircraft,parking at A1 to A26 in Fig.1,are assigned for weapon support operations for Type II and Type III weapons,at the same time 10 aircraft,parking at A1 to A10,have been mounted with 4 weapons with Type I which must first be unmounted and delivered back to the WSC.This is a large-size WTSSPPD.

For all the mission cases,there are two types of support units driven by manpower(M)and electricity(E)on deck,their numbers are 6 and 3,respectively.Number these support units from 1 to 9.Time consumption for the two types of support units to unmount a weapon with Type I,mount a weapon with Type II and Type III is presented in Table 2,and the maximum capacity of the two types of support units to carry the three types of weapons is shown in Table 3.Of the four weapon mounting points of each carrier aircraft for all the mission cases,two on the outer side need to be mounted weapons with Type II,and two on the inner side need to be mounted weapons with Type III.

7.2.Parameter setting of the proposed BPIA

The combination of different parameters may directly affect the performance of the proposed algorithm,so the Taguchi method[37]is employed to determine the optimal parameter set.Four different factors critical to the proposed BPIA with three different levels(see Table 4)for the proposed BPIA are tested.The orthogonal array used in this study isL9(34）.Each parameter combination is independently tested 10 times in each of the above three mission cases.And in each test,the proposed algorithm terminates after 10,000 schedule generations.The average response value (ARV) is defined as the average values of the objective-function value as shown in Eq.(26),wherefklis thel-thobjective-function value ink-thmission case generated by the BPIA.

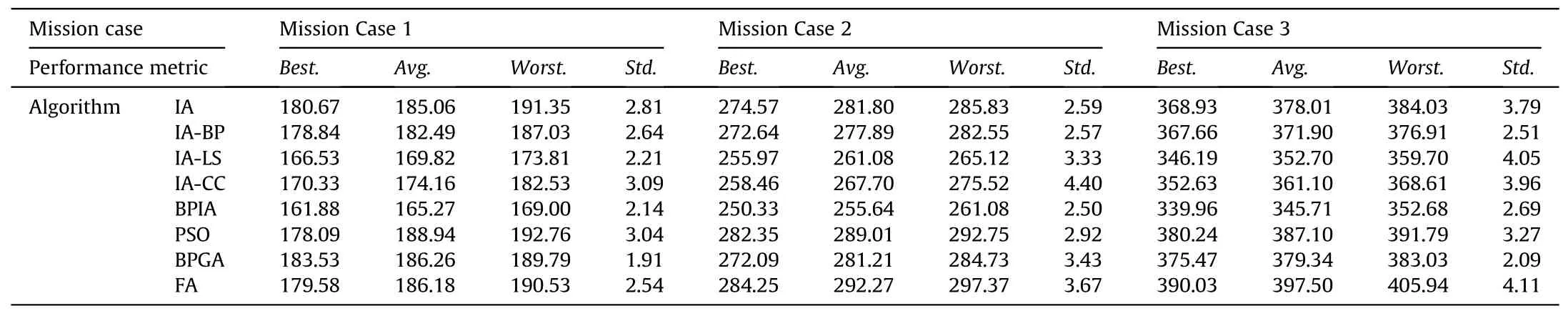
Table 6 Comparison of experimental results.

Table 2 Time consumption of different support unit for supporting different weapons(min).

Table 3 Capacity of support unit for different type of weapons.

Table 4 Combination of parameter values.

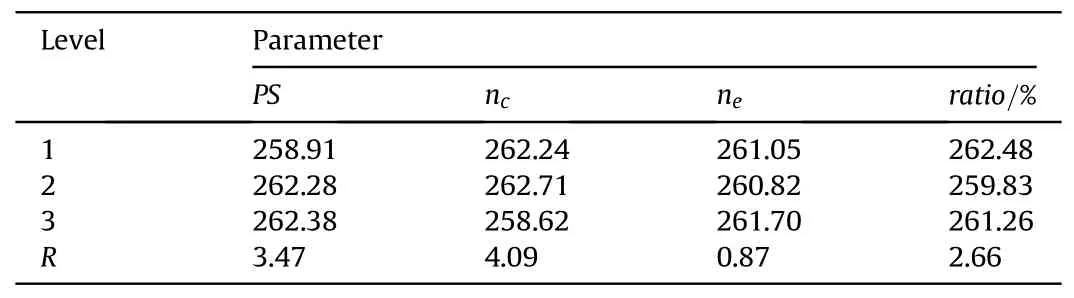
Table 5 Response table for average ARV of each parameter.

Fig.8.The best evolutionary convergence curves of the experimental algorithms in Mission Case 1.

The response for average ARV of each level of different parameters is shown in Table 5,in whichRis the range of average ARV for each parameter.A larger range value indicates a higher influence of the corresponding parameter on the solution.Thus,it is easy to findncis the utmost significant parameter for the BPIA,followed byPS,ratioandne.Based on the minimal average ARV,the best combination of parameters isPS=20,nc=20,ne=40,ratio=70%.

7.3.Experimental comparisons and discussion

To verify the performance of the proposed BPIA for WTSSPPD,experimental comparisons are carried out in three mission cases.As far as we know,the existing literature rarely studies the optimization problem similar to the WTSSPPD.The comparison algorithms exploited in this section includes a bi-population genetic algorithm (BPGA) [35]for RCPSP,a particle swarm optimization(PSO)[21]for solving the VRPSPD,and a firefly algorithm(FA)[38]for solving the VRP.Besides,we introduce the proposed optimization operators one by one on the basis of immune algorithm to verify the effectiveness of the proposed operators.The immune algorithm is abbreviated as IA,the immune algorithm combined with forward/backward scheduling technique is abbreviated as IABP,the immune algorithm combined with four local search schemes is abbreviated as IA-LS,the immune algorithm combined with a chaotic catastrophe operator is abbreviated as IA-CC.The parameters of these four algorithms are the same as the proposed BPIA and same SGS and decoding scheme are used.The parameters for executing the chaos catastrophe operator in BPIA and IA-CC are set: the population invalid iteration thresholdLimit=5,and the number of cyclic mutation (Algorithm 5) operationsnw=3.The parameters related to objective-function value calculation are set:wl=[0.8，0.3],wt=[0.6，0.1],γ=[1，0.5],and the time of unloading and loading a weapon at WSC is 1 min.

All algorithms are coded using Spyder 5.0.5 (Python 3.7) on a personal computer with an Intel® Core™i7 processor and 16 GB RAM.Each algorithm is run independently 20 times with the maximal schedule generation numberNs=10000 in each mission case.The performance of each algorithm is evaluated by calculating the optimum(Best.),average value(Avg.),worst value(Worst.)and standard deviation (Std.) of the 20 objective-function results.The comparison results are shown in Table 6.And the optimal evolutionary convergence curve of the 8 algorithms on Mission Case 1 that is taken as example is depicted in Fig.8.

It can be seen from Table 6 that the proposed BPIA for all cases significantly outperforms other algorithms inBest.,Avg.andWorst.In addition,Std.obtained by BPIA is only larger than that of the BPGA in Mission Case 1 and 3 and better than that obtained by other algorithms.This proves,to some extent,that the forward/backward scheduling technique helps to achieve robust scheduling results.

Compared with the basic immune algorithm,each algorithm developed by the introduction of one of key operators has improved the performance in terms of results,which lays out that these operators can effectively enhance the performance of the immune algorithm on WTSSPPD.Comparisons among the results obtained by IA-BP,IA-LS and IA-CC in three mission cases show that the chaotic catastrophe operator and local search schemes can greatly improve the global optimization performance of immune algorithm,and also can prove that the forward/backward scheduling technique can effectively improve the robustness of immune algorithm although it does not significantly enhance the algorithm's global optimization ability.

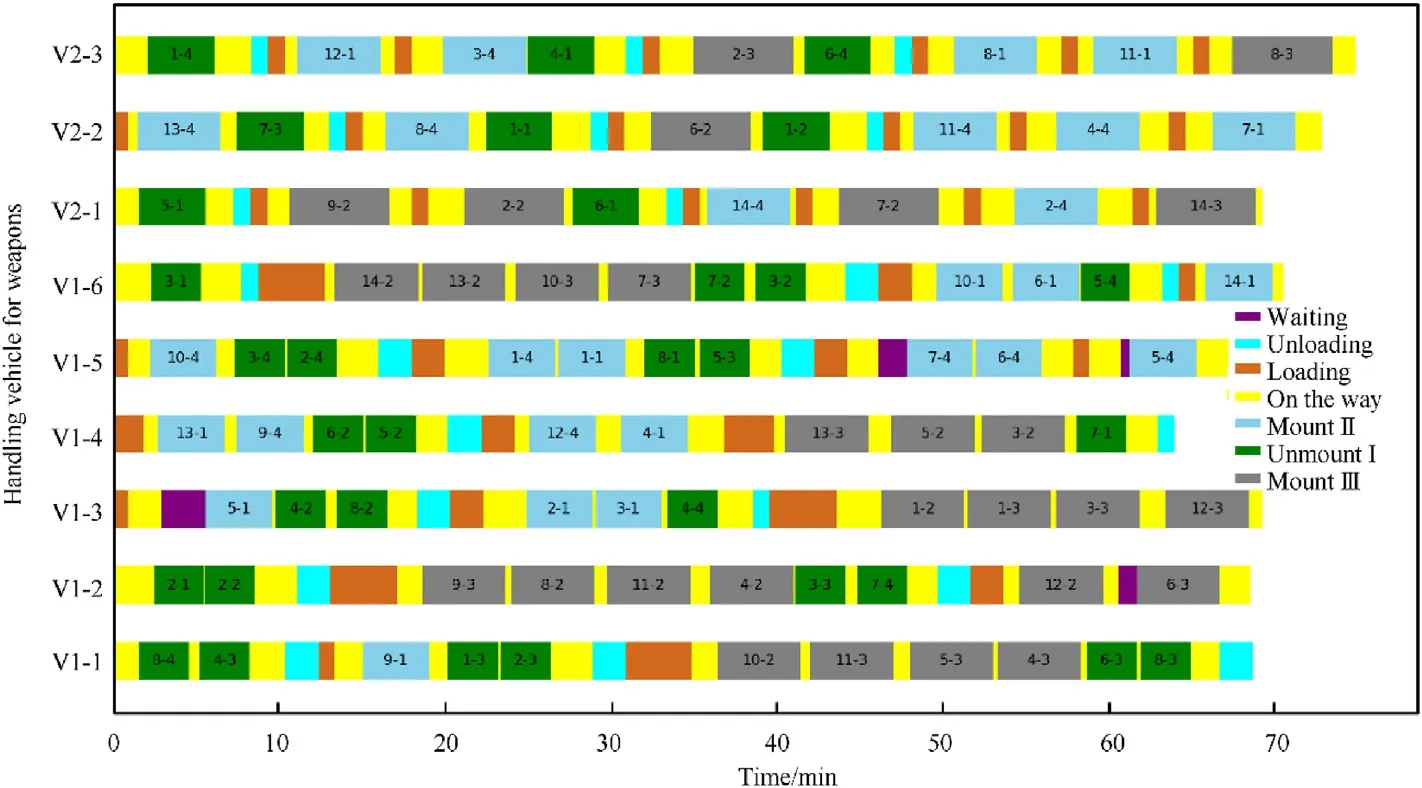
Fig.9.The Gantt chart of the optimal schedule generated by BPIA in Mission Case 1.

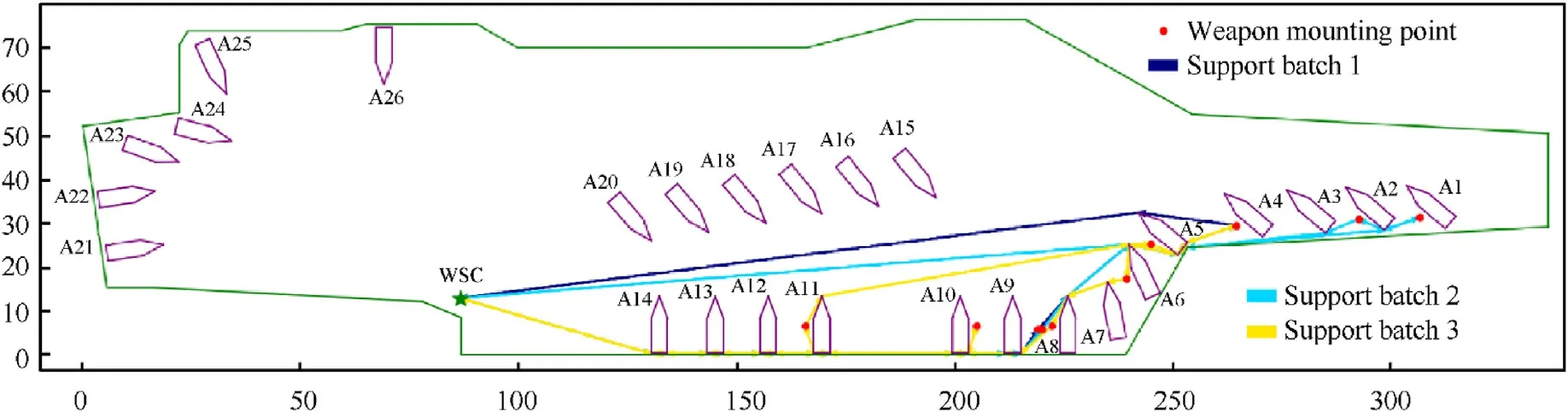
Fig.10.Support path example of a support unit.

As for other three comparison algorithms,their performance on WTSSPPD is not much different and is far inferior to BPIA.In smallscale WTSSPPD,their performance is comparable to IA and IA-BP.With the expansion of the scheduling scale,their performance,relative to BPIA,decreases rapidly.For PSO and FA,there is no scheme to deal with the precedence constraints in WTSSPPD,such as the insertion attempt in Algorithm 2.These absences usually will result in a long waiting time for support unit.Although the BPGA can handle the precedence constraints in WTSSPPD,its global optimization capability is insufficient.

The optimal running results of all algorithms are shown in Fig.8.From Fig.8,it is obvious that the proposed BPIA outperforms other algorithms in view of the results on WTSSPPD.It is also noteworthy that the local search schemes and the chaotic catastrophe operator in the proposed algorithm can significantly reinforce global search capability,and the IA-BP easily falls into a local optimal solution.As for other four algorithms,their optimization capabilities on WTSSPPD have defects to varying degrees.

The Gantt chart of the optimal schedule generated by the proposed BPIA in Mission Case 1 is shown in Fig.9.In the figure,thexaxis is the time course,and they-axis represents the type and number of the handling vehicles equipped by the corresponding support unit.For instance,V1-3represents the third handling vehicle in the first category.The colored boxes marked with numbers indicate the process of weapon support operations performed by the support unit.The green box indicates the process of unmounting Type I weapons,the sky-blue box indicates the process of mounting Type II weapons,and the gray box indicates the process of mounting Type III weapons.Boxes without numbers indicate the preparation process of weapon support operations.Chocolate color box indicates that the support unit is loading weapons at the WSC,cyan box indicates the process of unloading weapons on the WSC,yellow box indicates that the support unit is transporting weapons on deck,and purple box indicates that the support unit is waiting at the weapon mounting point for mounting weapons.The number marked on the box indicates the location of the weapon support operation.For example,the number 8-4 marked on the green box in the lower left corner of the graph indicates the support unit is performing an unmounting operation at the 4th weapon mounting point of the 8th carrier aircraft.

In Fig.9,the specific support progress of each support unit is presented,and it takes about 75 min to complete all weapon support operations in Mission Case 1.At the same time,it deserves our attention that in the optimal schedule,the support unit tends to perform the same number of weapons support operations as the maximum carrying capacity of the handling vehicle for weapon in each support batch.In addition,the waiting time of support units is rarely found in the optimal schedule.Thirdly,the number of operations done by each support unit is relatively even.In other word,the load balance of support unit is good.Based on these phenomena,it may be concluded that to optimize the objectives set in the paper can generate an efficient schedule.

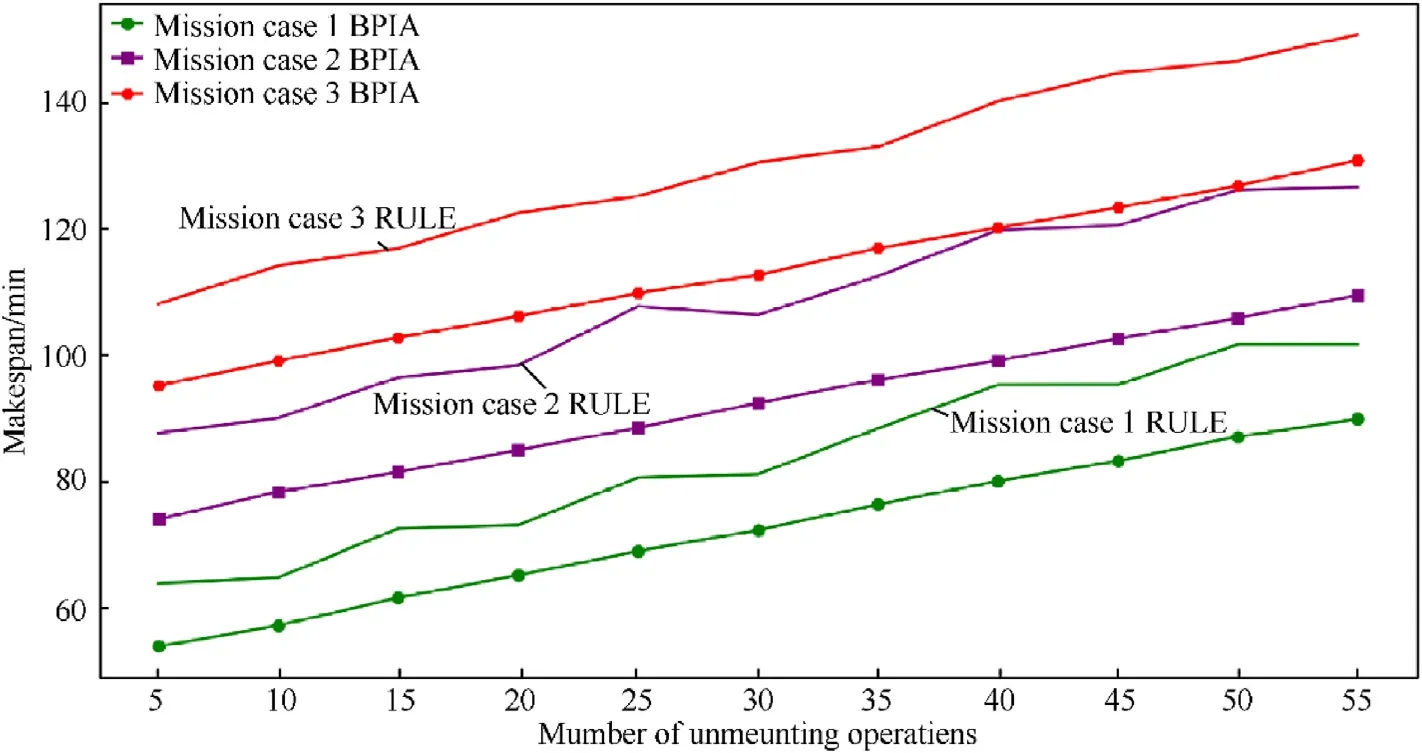
Fig.11.Completion time curves in three mission cases.

Based on the optimal schedule and the weapon transportation path library,taking support unitV1-1in Fig.9 as an example,its support path is presented in Fig.10.In Fig.10,the purple pentagon represents the previously established convex hull model of the carrier aircraft.The support unit carries out three batches of weapon support operations whose support path meets the deck obstacle constraints,and the support unit travels the shortest path when transferring between any two operation locations.

7.4.Analysis of number of unmounting operations

Previous research has been dedicated to maintaining the lasting support capability of the support unit.Sometimes,however,completing the weapon support task quickly is the first.Therefore,we consider the impact of the number of weapons that need to be unmounted on the completion time of support unit without paying attention to the other two objective functions.Based on above mission cases,we set the range of the number of weapons to be unmounted from 5 to 55,and the value interval is 5.In addition,we employ the support rule(RULE)used in practice as a comparison.In RULE,the support unit first completes weapon unmounting operations,and then performs weapon mounting operations of a single carrier-based aircraft one by one.The experimental results are presented in Fig.11,in which the result of the proposed algorithm is the average of ten runs.

In Fig.11,different mission cases correspond to different sortie missions,in each of which different quantities of unmounting operations result in different weapon support tasks.It can be seen that in all three mission cases,the mission completion time of weapon support task obtained both by BPIA and RULE,has a linear relationship with the number of unmounting operations,rather than the exponential.Specifically,compared to the result obtained by RULE,the result of the BPIA is more linear,and the completion time obtained by the BPIA is shorter than that of RULE under the same number of unmounting operations in the same mission case.At the same time,we also notice that the completion time obtained by RULE rises in steps with the number of unmounting operations,which might be accounted for by the number of support unit.To sum up,we conclude that the proposed model and algorithm can generate a quick support schedule under different sortie missions,and effectively handle the demand of carrier-based aircraft weapon support tasks.

8.Conclusion and future work

In this paper,we address the WTSSPPD and establish a comprehensive model.The novelty of our model mainly lies in three aspects.(1)The carrier aircraft parking on deck is regarded as convex obstacle to the handling vehicles for weapons and support personnel.(2)There exists the precedence constraint between two operations in a weapon mounting point that has both a pickup demand and a delivery demand.(3) We consider the time of loading or unloading weapon at WSC according to the number of weapons.The model aims at minimizing the makespan,load variance and accumulative transfer time of the support unit.The three objectives are integrated in a lexicographic order based on the AHP.To solve the model effectively,we firstly construct a path library of weapon transportation through visibility graph method and Warshall-Floyd method.Then a BPIA is proposed for the WTSSPPD to generate schedule.In the algorithm,random-key solution representation and serial SGS are employed.Besides,a forward/backward scheduling technique,local search schemes and a chaotic catastrophe operator are incorporated into our proposed algorithm.Experimental results and comparison with multiple algorithms highlight that the proposed algorithm can achieve promising results.Ultimately,we analyze the impact of number of unmounting operations,and conclude that the model established and the algorithm proposed in this paper can well deal with the requirements of weapon support task under different sortie missions.

In the future,two directions might be studied intensively.On the one hand,more efficient methods are expected to be considered for the WTSSPPD.On the other hand,an array of uncertain factors may affect the WTSSPPD,thus the dynamic scheduling methods should be taken into consideration.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors are grateful for the financial support of the National Natural Science Foundation of China (No.52102453).