岩溶塌陷区埋地管道的挠度和应力分析*
李乔楚,庄 波,李联合
(西南石油大学,成都 610500)
0 前 言
由于埋地输气管道与岩土直接接触,不可避免地受到岩土活动的影响[1]。我国西南一带岩溶面积占地区幅员面积的三分之一以上[2-3],地震、滑坡等地质灾害频发,降水量较大,极易引发岩溶塌陷导致埋地管道变形、悬空甚至断裂。
国内外相关学者针对土体塌陷作用下埋地管道的力学响应开展了一系列研究。为了研究不均匀地层沉降对埋地管道受力变形的影响,E.Winkler[4]提出“Winkler 弹性地基梁理论”,此理论以弹性梁模拟埋地管道,将管道周边土体积视为具有一定拉压刚度且相互独立的弹簧。高田至郎[5]将穿越沉陷区与非沉陷区的管道均视为弹性地基上的连续梁模型,得到了地层沉陷作用下埋地管线力学分析的简化计算公式。高惠瑛[6]提出采用三次曲线方程模拟沉陷区域管道的力学特征,弥补了高田至郎计算公式不能完全适用最大沉陷发生在沉陷区域边缘有限远处时的问题。1998 年,Luo和Peng[7]以具有刚性接头的薄壁管道作为研究对象,采用梁模型模拟了管道在地层沉陷作用下的力学响应特征。王小龙[8-9]基于Winkler弹性地基梁理论,建立了埋地管道在局部悬空时与土壤相互作用的力学模型。陈阿锋[10]考虑到前人的研究大多针对刚性管道,而柔性管道由于不具备抗弯刚度所以在受力特性、破坏形式上存在特殊性,因此基于材料力学中的悬索受力模型模拟埋地柔性管道。王晓霖[11]以大柔度钢制管道作为研究对象,建立三维力学分析模型,基于概率积分法对开采沉陷区埋地管道沿线地表的下沉趋势进行预测。Kouretzis[12]考虑到不同延展性能对管道力学响应存在一定影响,采用双曲线方程模拟不同材质管道在地层沉陷影响下的力学特征。Gregory C.Sarvanis[13]利用等效静态模型计算沉降管道的横向变形长度,提出了一种土层错动作用下管道最大应变的简化计算公式。
Winkler 弹性地基梁通过“土弹簧”模拟管周土对管道的力学作用,由于其具有简捷易懂、便于工程应用等优点,因此已被国内外学者应用于土体塌陷区埋地管道的力学分析。但弹性地基梁模型的求解存在两个假定条件:一是假设管道与土体具有相同的沉陷量,二是要求变量x趋于无穷大,即模型仅适用于最大塌陷点发生在距离塌陷区域边缘无穷远处的情况。然而在实际土体塌陷过程中,土体和管道均会发生大变形,且最大塌陷点往往发生在塌陷区域边缘外侧的有限范围内,因此将塌陷区域埋地管道视为弹性地基梁模型的方法在适用性上存在一定的局限性。与此同时,现有研究涉及岩溶塌陷这一特殊地质灾害的较少,但近年来在各种自然或人为因素影响下岩溶区域埋地管道时常遭受土体塌陷作用。鉴于此,本研究建立岩溶塌陷区埋地管道的力学分析模型,针对非塌陷影响区和塌陷影响区分别采用Winkler 弹性地基梁和弹性基础上的连续梁开展分析,结合变形协调方程探讨埋地管道的挠曲变形,并进一步从管道载荷、轴向应力、环向应力和径向应力四个方面提出等效应力的计算方法,通过与ABAQUS 有限元模拟结果进行对比,验证计算方法的有效性,以期弥补采用弹性地基梁模型模拟塌陷区埋地管道不符合实际情况的缺陷,并在满足精度要求的同时简化岩溶区埋地管道工程的力学分析过程。
1 岩溶塌陷区埋地管道力学响应理论解析法
岩溶塌陷是指在具备岩溶洞隙、一定厚度松散盖层以及地下水活动等基本形成条件的基础上,地下岩溶土洞在重力、地震以及人为因素等多重影响下逐步向上发育扩展直至顶板承受载荷超过强度极限,最终顶板破裂、土洞坍塌的现象。随着顶板坍塌破裂,岩溶覆盖层土体不断向土洞内下陷,并对塌陷区域上部一定范围内的埋地管道造成影响,即存在相应的岩溶塌陷影响区长度lty,通常在沙土中取塌陷量大于0.01 倍岩溶覆盖层厚度的管道长度,在粘土中取塌陷量大于0.1 倍岩溶覆盖层厚度的管道长度进行分析[14]。
岩溶塌陷范围伴随着顶板裂口的逐步发育而不断扩展,在此过程中塌陷土洞两侧的非塌陷影响区管道受到未下陷土体的支撑作用,因此可将此区域视为Winkler 弹性地基梁。在岩溶塌陷过程中,覆盖层土体的塌陷范围随着土洞顶板裂口的发展而逐步扩大,从力学角度看,即土洞上部的塌陷影响区管道在竖直方向上受到的支撑力逐渐减小,并以地下岩溶土洞为中心呈现出“中间大、两头小”的连续变形特征,因此可将塌陷影响区管道视为弹性基础上的连续梁,以弥补采用弹性地基梁模型模拟塌陷区埋地管道不符合实际情况的缺陷。假定岩溶塌陷区埋地管道的变形及受力特征沿塌陷区域中心对称,以未变形管道的中心轴线为x轴构建全局坐标系,建立埋地管道简化力学模型,如图1 所示。

图1 埋地管道简化力学分析模型
1.1 非岩溶塌陷影响区域埋地管道力学分析
因所构建的力学解析模型以塌陷区域中心对称,故以右侧的非塌陷影响区域管道为例开展力学分析。基于Winkler 弹性地基梁理论,可将B点外侧管道视为右侧无限长度的弹性地基梁,单位长度管道受到上覆土体压力、管道自重、输送介质质量构成的均布综合荷载设为q(x),通过施加弯矩MB与剪力QB模拟塌陷影响区域管道对B点的力学作用,以B点为圆心、管道轴线为x轴构建局部坐标系x' -y',非塌陷影响区域埋地管道力学解析模型如图2 所示。

图2 非塌陷影响区域埋地管道力学解析模型
设定非塌陷影响区域埋地管道的变形特征遵循曲线y=f(x),则管道上侧均布的土体载荷总集度为
基于弹性力学理论,在均布综合荷载q0(x')、弯矩M(x')、剪力Q(x')三者耦合影响下,非塌陷影响区域管道的挠度y'及管—土间的相互作用压力ps(x')遵循以下力学关系
将式(1)代入上述力学方程,通过进一步推导可以得出
式中:E——管道弹性模量,Pa;
I——管道惯性矩,m4;
D——管道外径,m;
t——管道壁厚,m。
1867 年,国外学者Winkler 基于力学解析提出:理想化土体表面任意一点的受力大小与此点的位移存在线性关系,即为Winkler弹性地基梁假设。基于此假设可将管—土间的相互作用压力表示为ps(x')=Ky',将其代入式(5)可推导得出
式中:K——地基弹性抗力系数,N/m3。
由于B点外侧的非塌陷影响区域管道被视为右侧无限长度的弹性地基梁,当假定此区域仅受到弯矩MB及剪力QB的作用而不考虑均布综合荷载产生的影响时,式(7)可转化为
通过齐次微分方程分析,非塌陷影响区域埋地管道挠度方程的通解可表示为
式中:λ——特征系数,λ=;
c1、c2、c3、c4——方程待定系数。
岩溶塌陷对埋地管道的力学作用由塌陷中心向两侧逐渐减弱,故当x→∞时,岩溶塌陷引起的管道位移可近似为0,将此边界条件代入微分方程即可反推得到方程通解的待定参数c1=c2=0,此时式(9)可转化为
当塌陷影响区域右侧边界B点仅受到弯矩MB的作用而不考虑剪力QB及均布综合荷载产生的影响时,式(2)及式(4)可转化为
将式(10)的导数代入(11)即可反推得到通解的待定参数c3=-MB/2λ2EI,c4=MB/2λ2EI,此时得到管道挠度方程的一个特解为
依据λ=消除参数EI,式(12)可转化为
当塌陷影响区域右侧边界B点仅受到剪力QB的作用而不考虑弯矩MB及均布综合荷载产生的影响时,式(2)及式(4)可转化为
将式(10)的导数代入(14)即可反推得到通解的待定参数c3=QB/2λ3EI,c4=0,此时得到管道挠度方程的另一个特解为
依据λ=消除参数EI,式(15)可转化为
当非塌陷影响区域管道仅受均布综合荷载作用时,可得管道挠度方程的第三个特解为
联立式(13)、(16)和(17)对应的三个特解,即可得式(8)的解为
令x=x'+lty/2,y=y',则将非岩溶塌陷影响区域埋地管道的挠度方程由局部坐标系转至全局坐标系,即当x≥lty/2 时,埋地管道的挠度方程可表示为
此时B点右侧非岩溶塌陷影响区域埋地管道任意截面的转角θ、弯矩M以及剪力Q可表示为
由于岩溶塌陷区埋地管道的变形及受力特征沿塌陷区域中心对称,即当x≤-lty/2 时,A点左侧非岩溶塌陷影响区域埋地管道任意截面的转角θ、弯矩M、剪力Q可表示为
非岩溶塌陷影响区域边界A、B两点的挠度和转角可表示为
1.2 岩溶塌陷影响区域埋地管道力学分析
岩溶塌陷区埋地管道的变形及受力特征沿塌陷区域中心对称,且塌陷影响区域管道与非塌陷影响区域管道在交界点处满足力学连续性,通过弯矩MB与剪力QB模拟非塌陷影响区域对塌陷影响区域的力学影响,并利用简支支座代替剪力,以A点为圆心、管道竖向下沉后的中心轴线为x轴构建局部坐标系x" -y",即x" =x+l/2,y"=y-yB,塌陷影响区域埋地管道力学解析模型如图3所示[15]。

图3 塌陷影响区域埋地管道力学解析模型
当塌陷影响区域管道仅受到均布综合荷载Qu作用时,可得管道挠度方程的一个特解为
当塌陷影响区域管道右侧边界B点仅受到弯矩MB作用时,可得管道挠度方程的另一个特解为
当塌陷影响区域管道左侧边界A点仅受到弯矩MB作用时,可得管道挠度方程的第三个特解为
联立式(28)、(29)、(30)对应的三个特解,即可得到塌陷影响区域埋地管道挠度方程的解为
此时岩溶塌陷影响区域埋地管道任意截面的转角θ、弯矩M以及剪力Q可表示为
岩溶塌陷影响区域边界A、B两点的挠度和转角可表示为
基于变形协调理论,塌陷影响区域管道与非塌陷影响区域管道在交界点处满足力学连续性。由式(26)及式(36)可得,交界点A和B处的管体挠度相同,此时为了保证转角符合连续性条件,只需令式(27)及式(37)对应的数值相等,即
根据式(35)可得B点的剪力QB为
将式(39)代入(38)即可得到B点的弯矩MB为
综上所述,通过保证塌陷影响区域及非塌陷影响区域交界点处管道挠度y、转角θ、弯矩M、剪力Q的数值一致性可以实现岩溶塌陷区埋地管道力学性能的连续性。
1.3 岩溶塌陷区埋地管道等效应力分析
1.3.1 管道荷载分析
单位长度管道受到的上覆土体压力、管道自重、输送介质质量可简化为方向竖直向下的均布综合荷载,即
式中:Qu——管道承受的均布综合荷载,N/m;
q1——管道上覆土体压力,N/m;
q2——管道自重,N/m;
q3——输送介质量,N/m。
管道上覆土体压力q1[16]可表示为
式中:γ——土壤的容重;
K0——横向土压力系数,对于粘性土取为0.65;
H——管道埋深,m;
D——管道外径,m。
管道自重q2可表示为
式中:A——管道横截面面积,m2;
ρp——管材密度,kg/m3;
d——管道内径,m。
对于埋地燃气管道,输送介质质量q3表示为
式中:P——管道内压,MPa。
1.3.2 管道轴向应力分析
图4 所示为岩溶塌陷区埋地管道轴向应力,参照已经发现的地层塌陷区域埋地管道轴向力的作用规律[17],在实际管道工程中,当塌陷土体长度不超过50 m 时,轴向力对管道力学响应的影响可以忽略不计。本研究的岩溶塌陷范围均未达到上述数量级,因此可不考虑轴向力对埋地管道等效应力产生的影响。

图4 岩溶塌陷区埋地管道轴向应力示意图
在岩溶塌陷过程中,由于管道沿线土体的下沉幅度存在差异,埋地管道随土层错动承受弯矩作用并在管道轴向发生弯曲变形,由弯矩作用引起的管道轴向应力可表示为
式中:σat1——弯矩作用引起的管道顶部轴向应力,Pa;
σab1——弯矩作用引起的管道底部轴向应力,Pa。
在日常运行工况下,埋地管道为了输送介质还将承受内压产生的力学作用,将内压引起的轴向应力代入式(45),即可得到岩溶塌陷区埋地管道的轴向应力计算公式
式中:σat——管道顶部的轴向应力,Pa;
σab——管道底部的轴向应力,Pa;
D——管道外径,m;
υ——管道泊松比;
t——管道壁厚,m。
1.3.3 管道环向应力分析
图5为内压作用下埋地管道环向应力 ,由管道内压作用引起的环向应力可表示为
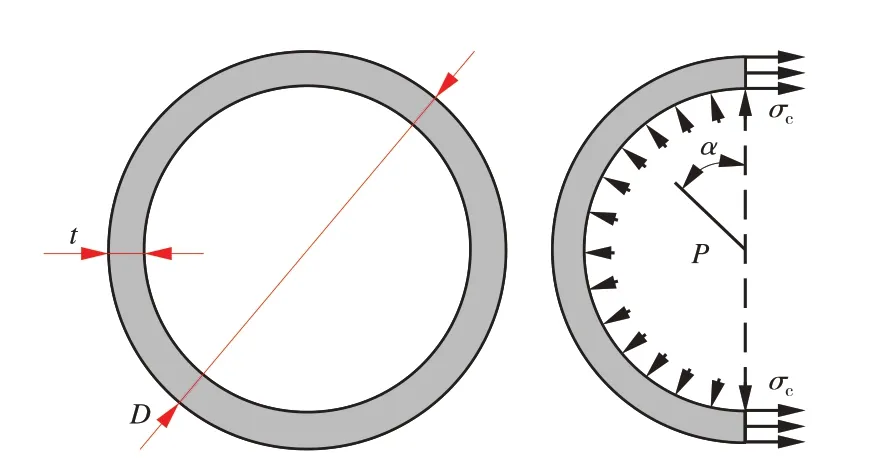
图5 内压作用下埋地管道环向应力示意图
1.3.4 管道径向应力分析
图6为内压作用下埋地管道径向应力,径向应力沿着管径方向由内向外作用于管道,由管道内压作用引起的径向应力可表示为
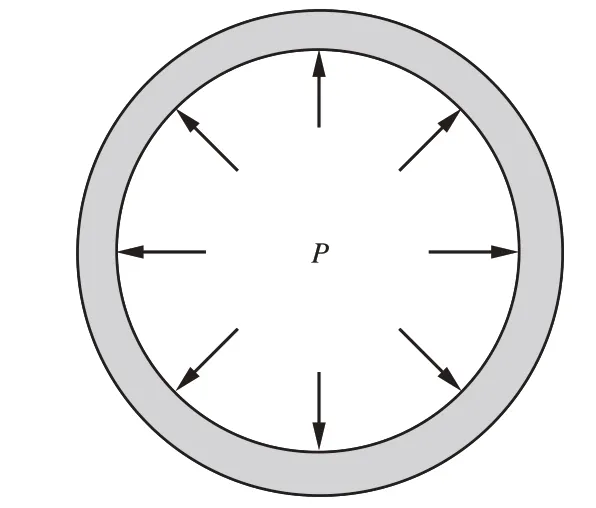
图6 内压作用下埋地管道径向应力示意图
综合上述,通过分析埋地管道轴向、径向、环向的应力,结合Von Mises 屈服准则即可得到岩溶塌陷区埋地管道的等效应力计算公式
式中:σMt——管道顶部的Mises 等效应力,Pa;
σMb——管道底部的Mises等效应力,Pa。
2 算例分析
贵州某岩溶区段位于纳雍—开阳东西向构造带与织金北东向构造带的交汇处,近年来在矿山无序开采、地下洞穴发育、持续强降雨及地震活动等多重因素影响下,每年发生明显地面塌陷40 余次,并呈现出增加趋势。该区段内运行有一埋地燃气管道,管道材料为PE80,密度为950 kg/m3,管径为200 mm,壁厚为18.2 mm,内压为0.4 MPa,瞬态松弛模量为578.71 MPa。
为了验证本研究算法结果的准确性,基于ABAQUS 软件构建了图7 所示的岩溶塌陷区埋地管道有限元模型[18],采用4 节点Shell 单元、8 节点3D-Solid 单元分别对管道和土体进行离散建模,管—土采用3D-Contact非线性接触,重力加速度取9.8 m/s2。由于PE 管道具有粘弹性特性,基于Prony级数建立PE80 管材的本构方程[19]。考虑到岩溶区域地质结构复杂多变,将土体模型简化为素填土、粉质粘土以及基岩三种典型土层,选用Mohr-Coulomb 模型描述岩溶土体的非线性特征。由于PE 管道与管周土在法向和切向两个维度产生力学作用,采用“硬接触”描述法向行为,基于“罚函数”描述切向行为,摩擦系数设置为0.3。当岩溶土体塌陷长度为5 m、6 m、7 m、8 m、9 m 和10 m 时,基于弹性地基梁理论解析和基于ABAQUS 数值模拟得到的管道最大Mises等效应力数值见表1。

图7 岩溶塌陷区埋地管道有限元模型

表1 岩溶塌陷区埋地管道最大Mises等效应力
由表1 可知,岩溶塌陷区埋地PE 燃气管道最大Mises 等效应力的理论解析结果与基于ABAQUS有限元分析的数值模拟结果的平均相对误差为5.23%(<10.0%),处于可接受范围内,由此说明采用本研究算法开展岩溶塌陷区埋地管道的力学反应分析是合理的,在满足精度要求的同时可以简化岩溶区埋地管道工程的力学分析。
3 结 论
(1)通过构建的简化管-土相互作用理论模型开展岩溶塌陷作用下埋地管道的力学分析,与其他方法相比具有概念简单、计算方便、便于工程应用等优点。但现有研究中常用的Winkler 弹性地基梁假设管道与土体具有相同的沉陷量,且不适用于最大塌陷点发生在塌陷区域边缘外侧有限范围内的情况,本研究通过将塌陷影响区管道视为弹性基础上的连续梁,从而解决采用弹性地基梁模型模拟塌陷区埋地管道不符合实际情况的问题。
(2)通过与仿真结果进行对比分析,证明本研究方法的计算结果比较合理,能够在满足精度要求的同时简化埋地管道的力学分析,因此可用于岩溶区埋地管道的工程实践。但以上研究均是建立在一定约束前提下,对管土参数及边界条件进行了假设或简化;与此同时,由于弹性梁理论自身的局限性,其往往无法准确反映管道进入塑性阶段的力学行为,因此理论解析结果需要通过结合具体管材的强度极限数值开展有限范围内的力学响应研究。未来此领域为了开展更为深入的研究,建议将理论解析法与数值模拟法、试验分析法等联合使用。

