高超声速变构型飞行器气动布局优化设计
罗世彬 岳航 刘俊
(中南大学航空航天技术研究院 湖南省长沙市 410083)
更高、更快、更远一直是航空航天飞行器发展的主旋律,一般认为,来流空气流速Ma>5 为高超声速气流,飞行速度Ma>5 的飞行器为高超声速飞行器。因其具备前瞻性、牵引性和战略性的特点,高超声速巡航飞机、侦察机、空天飞机乃至高超声速客机已经成为新世纪航空航天的技术前沿之一,随着对水平起降的需求不断提升,实现宽域飞行是高超声速飞行器的重要发展方向与设计目标[1-2]。
在较宽的速域范围内,不同飞行条件的设计点下的飞行器展现出不同的布局特点,现阶段高超声速飞行器主要采用的典型布局方案主要有:升力体、翼身融合体、乘波体等[3],这些构型普遍具有着大展弦比、大长细比、大后掠角的布局特征,重点考虑了在高超声速阶段的气动特性,往往无法满足亚声速、跨声速、超声速状态的性能要求,一旦偏离设计状态气动性能急剧恶化。从不同飞行速域和任务类型飞行器之间的布局差异以及宽速域飞行器的设计难点问题中可以看出单一、固定的外形很难满足宽速域范围内多设计点的气动性能要求[4]。因此,合理的变构型设计可以有效的解决不同设计点下飞行器的设计矛盾。
随着高超声速飞行器外形越来越复杂以及变形需求的提出,外形设计需要兼顾诸多的限制和约束条件,对气动布局设计方法提出了更高的要求。随着计算方法和计算机技术的快速发展,根据最优化理论自动求解的方式进行气动外形设计的方法被广泛关注,这种方法的关键是将设计过程完全自动化,通过数学优化理论结合气动评估方法自动求解气动布局设计问题[5]。气动布局自动优化设计技术正因为具有智能性和相对更强的设计能力,被广泛应用于处理复杂的气动布局设计问题。
1 数值方法验证
1.1 数值方法
本文采用三维可压缩Navier-Stokes 方程组求解飞行器周围流场。雷诺平均N-S 方程的三维守恒形式可以用以下积分形式来表示[6]:
其中Q,FC,Fv的定义如下所示:
式中,ρ表示为控制体内气体的密度;u、v、w分别表示为控制体内气体在x、y、z三个方向的速度;E表示为控制体内空气的能量;nx、nv、nz分别表示为控制体内微元面 的外法向单位向量在x、y、z三个方向的分量;p表示为该微元面上的压强;H表示为控制体内气体的总焓;Vr表示为沿控制面微元的法向速度;Vb表示为微元面的法向运动速度。
1.2 验证计算模型
本节选取公开文献[7]中的空天飞机模型作为计算模型,通过数值模拟结果与风洞试验数据对比分析,验证本文高超声速外流场数值计算方法的有效性和准确性。空天飞机模型的长度为290mm,宽度为184.8mm,高度为58mm,具体尺寸如图1所示。

图1:空天飞机风洞试验模型及三维物理模型
空天飞机风洞试验的边界条件为:Ma=8.03,单位雷诺数为Re=1.13×107,总压7.8MPa,总温为893K,数值计算条件与风洞试验条件一致。
不同攻角下的升力系数和阻力系数与实验数据对比如图2 和图3所示,与风洞试验数据吻合较好。本文采用的数值方法能够有效的模拟高超声速飞行器的外流场特性,数值计算结果具有较高可信度。

图2:升力系数随攻角的变化

图3:阻力系数随攻角的变化
2 优化设计方法
目前,基于CFD 技术的气动布局优化设计技术主要有以下四个关键环节:
(1)对优化问题进行分析提出优化模型,建立优化方案;
(2)几何外形参数化和网格自动生成技术;
(3)基于GPU 的高效CFD 数值模拟方法;
(4)基于代理模型的高效优化算法。
2.1 几何外形参数化
本文的优化设计系统采用基于NURBS(Non Uniform Rational B-spline)非均匀有理 B 样条基函数的三维FFD 参数化方法[8]。FFD 方法的控制体内几何外形(表面网格点)全局坐标与正则坐标系下局部坐标转换关系的表达式为:
其中,Pi,j,k为控制点的全局坐标,Wi,j,k为与控制点Pi,j,k所对应的权重系数;Ni,p,Nj,m,Nk,n是NURBS 基函数NI、NJ、NK分别为3 个方向控制点的最大序号。
2.2 网格变形方法
网格自动生成技术主要分为网格重构和网格变形技术。网格重构技术的特点是外形参数化和网格重构是两个相对独立的步骤,对拓扑结构没有严格要求,参数化处理相对灵活,复杂外形适应能力强,但由于每次外形变化都要重新划分网格,因此效率相对较低。网格变形技术是直接或间接地对物面网格或者空间网格进行扰动变形,不需要进行网格重造,只需要在优化开始时提供初始网格。
本文采用课题组自主研发的基于代理模型和贪心算法(Greedy Algorithmg)的通用网格变形软件MeshDeform 对空间流场计算网格进行网格变形。
采用径向基函数网格变形方法[9],其基本形式如下:
2.3 基于GPU的CFD数值模拟方法
本文在对飞行器进行CFD 数值模拟时,采用一套基于GPU 的高效CFD 数值模拟程序,该程序求解雷诺平均NS 方程,有限体积空间离散、k-w SST 湍流模型,AUSMPW+迎风格式,数值模拟方法的有效性已经过在前文进行验证。
2.4 基于代理模型的高效优化方法及流程
本文的优化环节采用课题组开发的基于代理模型的通用优化程序,它可以求解任意单目标、加权系数的多目标、Pareto 多目标的无约束、多约束优化问题。采用拉丁超立方试验设计方法(LHS)在单目标优化设计空间中生成初始样本点,然后通过外部interface 程序计算得到单目标函数的初始样本点的响应值。根据前述的飞行器优化设计方法,构建基于代理模型的单目标三维气动外形优化设计系统[10],如图 4所示。

图4:基于代理模型优化设计流程图
3 气动布局优化设计
3.1 优化问题分析
如图5 所欧式,高超声速飞行器在巡航状态下小展长、大弦长的气动外形会降低巡航状态横向的稳定性,而在飞行器爬升阶段,由于飞行器飞行高度不高,大气密度较大,应尽可能降低翼面积、展长等参数,充分考虑飞行器承受的大动压和降低气动阻力。为了满足飞行器加速爬升小展长、大弦长和高超声速巡航阶段展长与机翼面积的设计要求,本文采用伸缩翼的变构型设计[11]。

图5:变展长高超声速飞行器气动外形示意图
选取来流马赫数Ma=3,飞行攻角α=4°作为助推爬升阶段的优化设计点,巡航状态的优化设计点为来流马赫数Ma=6,飞行攻角α=8°。飞行器单目标优化以外翼收回小展长状态阻力系数最小为优化目标。约束条件为:
(1)外翼收回状态升力系数不减;
(2)高速巡航段外翼展开阶段飞行器升阻比不减。优化设计的数学模型如下:
图 6 给出了设计变量的示意图,选取变构型高超声速飞行器机翼上的控制点作为优化设计变量,在机翼上下表面各取30 个设计变量[12],且选取的控制点仅沿y轴方向移动。

图6:设计变量示意图
3.2 优化结果与分析
图 7 给出了目标函数的收敛曲线,纵坐标为优化设计的目标值,即飞行器外翼回收段的阻力系数,优化总共进行了近180 次迭代寻优,在第137 次迭代后找到了最优设计点,优化后的气动外形和初始外形的对比图如图 8所示。
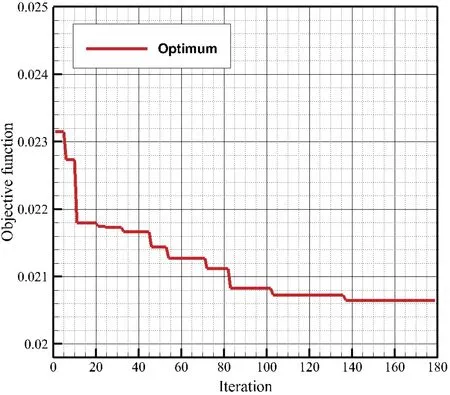
图7:目标函数收敛曲线
表 1 为优化外形与初始外形的气动力系数对比,可以看出,与初始外形相比,优化外形在外翼回收升力系数基本保持不变,阻力系数减小了0.001238,相对减少量为5.6%;外翼展开高速巡航段升力系数和阻力系数相对于初始外形变化较小,其升阻比增加了0.005,相对增加量为0.12%,在外翼回收阻力系数的同时并没有降低高超声速外翼展开状态的气动性能。
4 结论
本文结合FFD 几何外形参数化、径向基函数网格变形技术、基于GPU 的CFD 数值模拟方法、代理模型优化算法等优化设计方法,气动布局优化设计系统,利用该系统进行了气动布局优化设计。以外翼回收段飞行器的阻力系数最小为目标,外翼回收段升力系数和高速巡航段升阻比不增为约束条件,优化后外翼回收段阻力系数减小5.6%,约束条件得到满足。优化结果证明了本文方法的有效性。

