基于OpenMP技术探究并行体与并行数目对运行效率的影响
付颖
(黔南民族职业技术学院大数据与电子商务系 贵州省黔南布依族苗族自治州 558022)
1 OpenMP技术概述
1.1 OpenMP技术
从计算机发明之初,到现如今的人工智能的出现,计算机的快速发展已成为很多领域的核心力量。在本世纪的头10年,利用空气冷却技术制成的集成电路,其散热能力已经达到了该器件的极限。因此,通过不断加快集成电路的速率来提升处理性能的方法已经不再适用,既然计算方法对改善计算机处理性能有推动作用,那么继续发掘更强的计算机处理能力就是迫切且必要的,所以人们在研发新一代计算机的进程中,并行技术起着关键性的作用。并行技术是指在同一时间内,增添运算量的处理技术。然而在目前的发展过程中,并行软件的进展,极大程度上地滞缓于并行技术体系结构的进展;并行技术的使用,也极大程度上地较滞缓于并行技术的发展[1]。
随着并行技术的发展,市面上出现了形式不同的并行模型。比如基于程序构建的模型(CSP、Linda 等),基于问题阐述的模型(GAMMA、UNITY 等),基于并行理论的模型(PRAM、BSP 等)和硬件结构抽象模型(又称为自然模型)。而硬件结构的抽象模型又分为同享储存的模型和语言(PVP,SMP 等)在 Pthreads、OpenMP等环境下进行内存同享编程,讯息传送的模型和语言(适于MPP,Cluster 等)在MPI、PVM 等环境下进行分布式内存编程;数据并行的模型和语言(适合 MPP/Cluster上完成 SPMD 操作)在 Fortran、HPF 等环境下编程[2]。
OpenMP 技术是一种用于共享内存并行系统的多线程程序设计方案,支持的编程语言含C、C++和Fortran[3]。OpenMP 技术提供对并行算法的高层抽象描述,特别适合在多核CPU 机器上的并行程序设计,程序员课通过在源代码中添加专门的编译指示来表明自己的编程意图,由此编译器可以自动地将程序进行并行化,并在必要之处加入同步互斥以及通信。当选择忽略这些编译指示时,或者编译器不支持OpenMP 技术时,程序又可退化为通常的程序(一般为串行),代码仍然可以正常运作,只是不能利用多线程来加速程序执行[4-5]。
1.2 相关概念
串行计算:传统意义上的编程计算,指计算过程只能够按照计算机的执行顺序进行的计算,在同一个时刻中计算机只能进行一次运算。
并行计算:是一种快速的计算方式,是相对串行计算而言的,我们又把这种计算方式称为平行计算。传统的串行计算由“指令”与“数据”两部分构成,在代码施行时,内存空间是采取“独立应用和占有”的方式,而且在代码运行期间所有的运算都仅限于此。而并行计算,则是将计算相对独立的分配给不同节点的进程,通过它们自己独立的操作进行系统调度,享受独立的CPU和内存资源(即共享内存),进程中通过消息传递实现讯息的交换。它是一种一次能够施行多个命令的算法,是一个能够在同一时间内利用各种不同的计算方式求解计算问题的历程,是一种有效的提高计算速率和处理能力的运算方法。其根本思想是使用多个处理器来解决同样的问题。换言之,就是将问题分成几个部分,每个部分由一个单独的处理器进行解决的运算历程[6-7]。
进程:一个具有独立功能的程序关于某个数据集合的一次运行活动,是CPU 资源分配的最小单位。
线程:建立在进程的基础上的一次程序运行单位,被包含在进程之中,是CPU 调度的最小单位,也是进程中的实际运作单位。
并行体:并行计算的数据规模。
并行数目:并行计算的次数。
加速比:同一个任务在单处理器系统和并行处理器系统中运行消耗的时间的比率,用来衡量并行系统或程序并行化的性能和效果。
1.3 编译环境
在本文中所以涉及到的计算的软件环境是:64 位windows7 操作系统和CodeBlocks(版本13.12.0.0)编译器,编程语言:C、C++和OpenMP,硬件环境是:Intel(R)Core(TM)i3_2375M 的双核CPU(1.50GHz,1.50GHz),4G 内存,AMD Radeon HD 7450M 与Intel(R)HD Graphics 3000 双显卡(基本上已经是很落后的硬件环境,这种设备的机器能够在跳蚤市场以十分低廉的价钱获得),编译优化参数为-O2。
2 基于OpenMP技术探究并行体对运行效率的影响
本节在保持并行数目不变的情况下,改变数据规模的大小,基于OpenMP技术探究并行体对运行效率的影响。
以欧拉计划[8]145 题为例。欧拉计划是由Colin Hughes 发起的一个解题网站,目前这个网站包含了400多道难度不同的数学题,题目序号的增加与难度呈正相关,每一个问题都有相应的讨论社区,而且每个问题都可以在 1 分钟内通过计算机程序获得。
145 题的题目内容为:某些正整数n 有这种特殊的特征:N 和N 取“相反”相加以后的全部的位都是奇数。例如:36+63=99 或者409+904=1313,我们把这些特殊的数字作为可反数,因此36,63 等这些数都是可反数。但是在N 和N 取“相反”的最前端都不能有0,一千以内共含120 个可反数,问10 亿(即109)以内共含几个可反数?
利用计算机进行编程计算,可得到上述问题的正确答案为:60872。求解的串行计算伪代码为:

通过实际计算,改变并形体的大小,取三次平均耗时,得到串行计算的运算时间如表1所示。
接下来,采用并行(并行数目为2 次)编译方式,对上述欧拉145 题进行求解。将上述的串行伪代码改写为基于OpenMP 技术的并行伪代码:
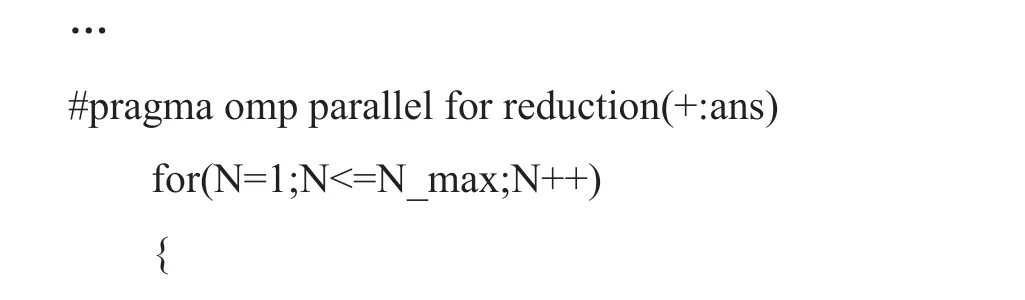

在测试环境近似相同且保证运算结果相同的情况下,改变并形体的大小,取三次平均耗时,可得到并行计算(并行数目为2 次)的运算时间如表2所示。

表2:欧拉计划145 题并行计算所耗时长
表3给出了欧拉计划145题串行计算与并行计算(并行数目为2 次)的加速比。显然,随着并形体的变化,即数据规模的不断增加,只有极少数情况下规模越大加速比越小,绝大部分情况下加速比与并形体规模大小呈正相关。

表3:串行计算与并行计算的加速比
通过表1 和表2 以及表3 的结果对比,直观地显示出了基于OpenMP 技术并行计算的优越性。在保持并行数目不变的情况下,随着并行体的规模逐步增大,并行计算对运行效率的影响越大,并行计算的优势体现得越明显。
3 基于OpenMP技术探究并行数目对运行效率的影响
本节在保持并行体不变的情况下,即设置并行体中的数据规模相同,改变并行数目的次数,基于OpenMP技术探究并行数目对运行效率的影响。
以蒙特·卡洛法[9](Monte Carlo)求解π值为例。蒙特·卡洛法也称为计算机的模拟方法,在20所示40年代由乌拉姆和J.冯·诺伊曼提出的一种基于“随机数”的计算方式。其根本思想是,当一个问题是某个事件发生的概率,或某个随机变量的数学期望时,它们能够通过一些“测试”,求出该事件的概率或者这个随机数的平均值,并以此来作为该问题的解。
利用蒙特·卡洛法求解π 值的串行伪代码如下:


通过该方法进行编程计算,得到的最大随机数为:32767。由蒙特·卡洛算法模拟出的半径为1 的1/4 圆的面积为:0.785428,计算出的pi 值为:3.14171。
在测试环境近似相同的情况下,分别在并行数目取1次(即串行计算)、取2次一直取到183次进行计算测试,其运算结果如表4所示。

表4:蒙特·卡洛法求解π 值计算所耗时长
由表4 的结果,得到并行数目与计算耗时关系如图1所示。
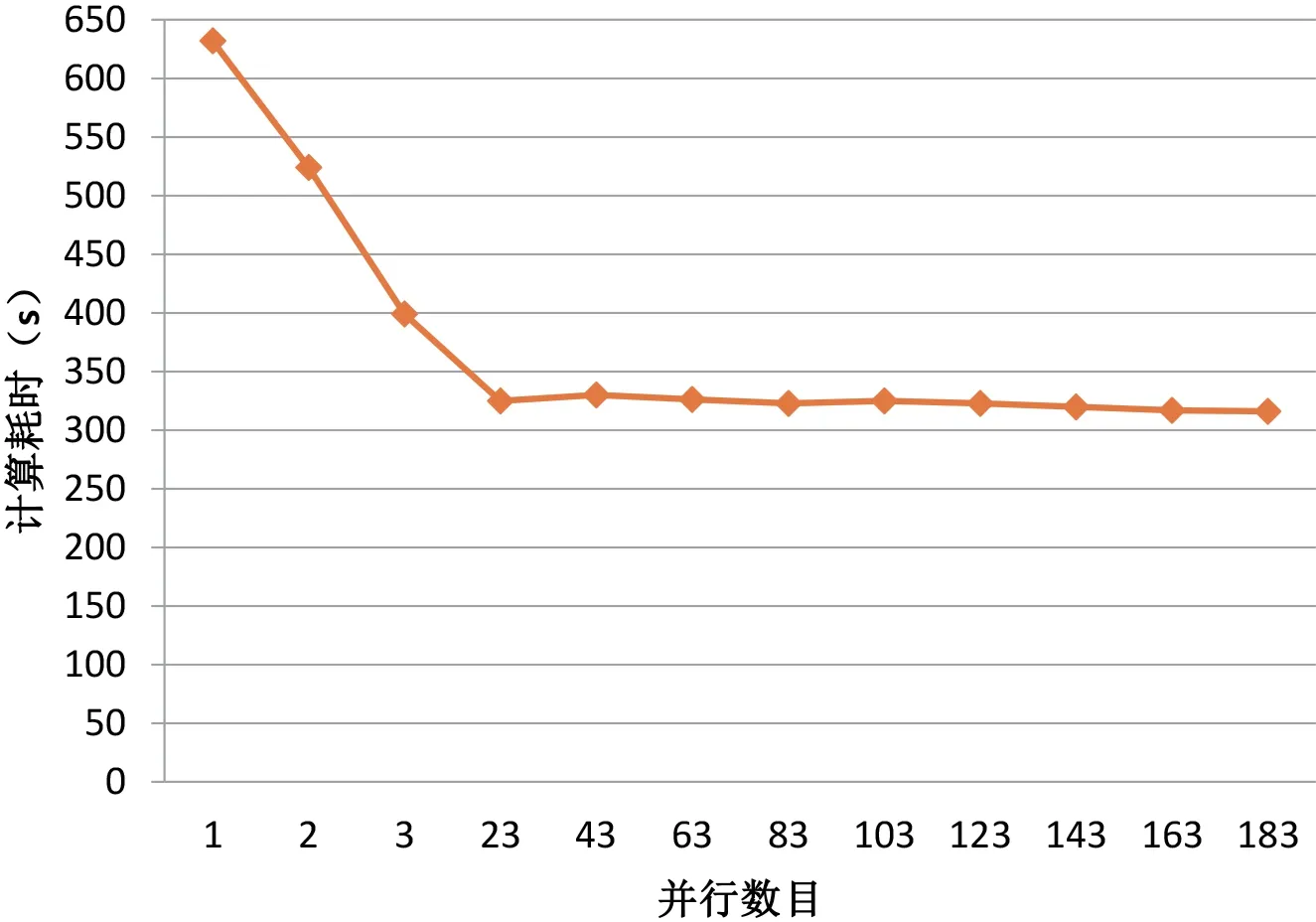
图1:并行数目与计算耗时的关系
通过表4 和图1 结果显示了,在保持并行体规模不变的情况下,且在CPU 物理极限范围内,并行数次数越高,并行计算对运行效率的影响越大,所需耗时越短,优势越显著,较好地体现了基于OpenMP 技术并行计算的优越性。
4 结语
本文基于OpenMP 技术进行并行计算,采用控制变量法的思想,以欧拉计划145 题为例,探究了并行体对运行效率的影响;以蒙特·卡洛法求解π 值为例,探究了并行数目对运行效率的影响。通过实际算例与原有串行方法相比较,验证了基于OpenMP 并行计算的优越性。但是,本文给出的两个计算实例,测试时运行环境只是相近,而非完全一致,系统中其他程序对测试结果还是造成了一定程度的干扰,且计算规模都稍偏小,大规模的并形体对运行效率的影响还需要进一步的研究。其次,测试的计算机(双核四线程)CPU 线程有限,并行数目也比较受限,多线程的并行数目对运行效率的影响还需要进一步的研究。

