基于改进蚁群算法的工业机器人路径规划研究

朱 敏, 肖 阳, 臧昭宇

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

路径规划是机械臂运动规划领域的重要研究课题之一,是指在已知的环境下,按照某种方法找出一条从起点到终点的无碰撞路径[1-4]。考虑到机械臂工作环境的日益复杂,路径规划的作用也越来越重要,许多智能优化算法也已经应用于相关领域中,如RRT算法[5]、人工势场法[6]、A*算法[7]、遗传算法[8]等。其中,蚁群算法[9]具有正反馈的特点以及并行计算的优势,已被广泛应用于解决路径规划等问题。为了进一步提高蚁群算法在机械臂路径规划中的效果,国内学者对蚁群算法进行了适当优化,文献[10]在蚁群算法中引入粒子群算法对其部分较优解进行变异和交叉操作,得到了更优的解;文献[11]采取改进的信息素更新策略和“惯性原则”完成最优操作路径的搜索;文献[12]提出建立可视域搜索空间和采用自适应调节挥发系数策略来加快蚁群算法的收敛速度;文献[13]结合人工势场法中强化目标路径的优点,提升蚁群算法的收敛能力,并有效缩短了算法的迭代次数。

本文提出一种改进的蚁群算法,将蚁群划分为外层蚁群和内层蚁群,分别设计不同的启发函数来提高搜索效率,并引入安全因子提高机械臂运动的安全性,先利用外层蚁群在无信息素的状态下规划出一条参考路径,增强该路径上的初始信息素浓度,优化信息素初值,同时改进信息素更新规则并对信息素浓度加以限制,进一步提升内层蚁群的全局寻优能力,搜索得到的最优路径经由一系列运算和约束得到机械臂的位姿集合,再导入到虚拟机械臂中,由机械臂的运动仿真实验可知,本文改进蚁群算法能为机械臂在不同环境中规划出一条符合运动要求的避障最优路径。

1 机械臂运动学建模

本文以品牌型号为IRB1600的六自由度串联工业机械臂为研究对象,相应的D-H参数见表1所列,机械臂的各个连杆坐标系如图1所示。

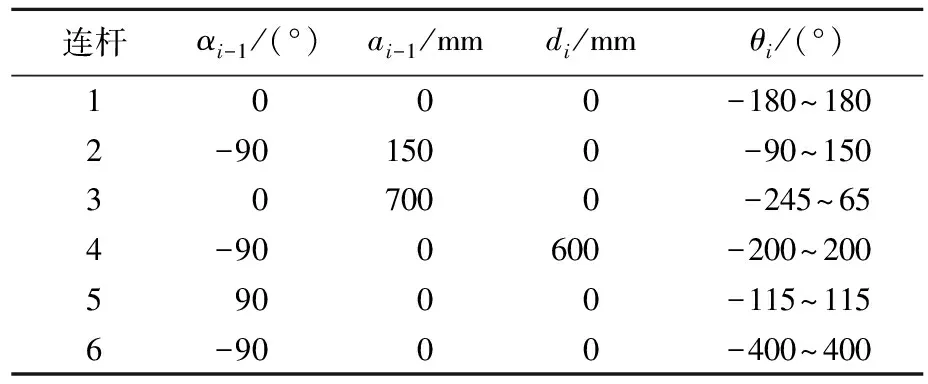
表1 IRB1600的D-H参数

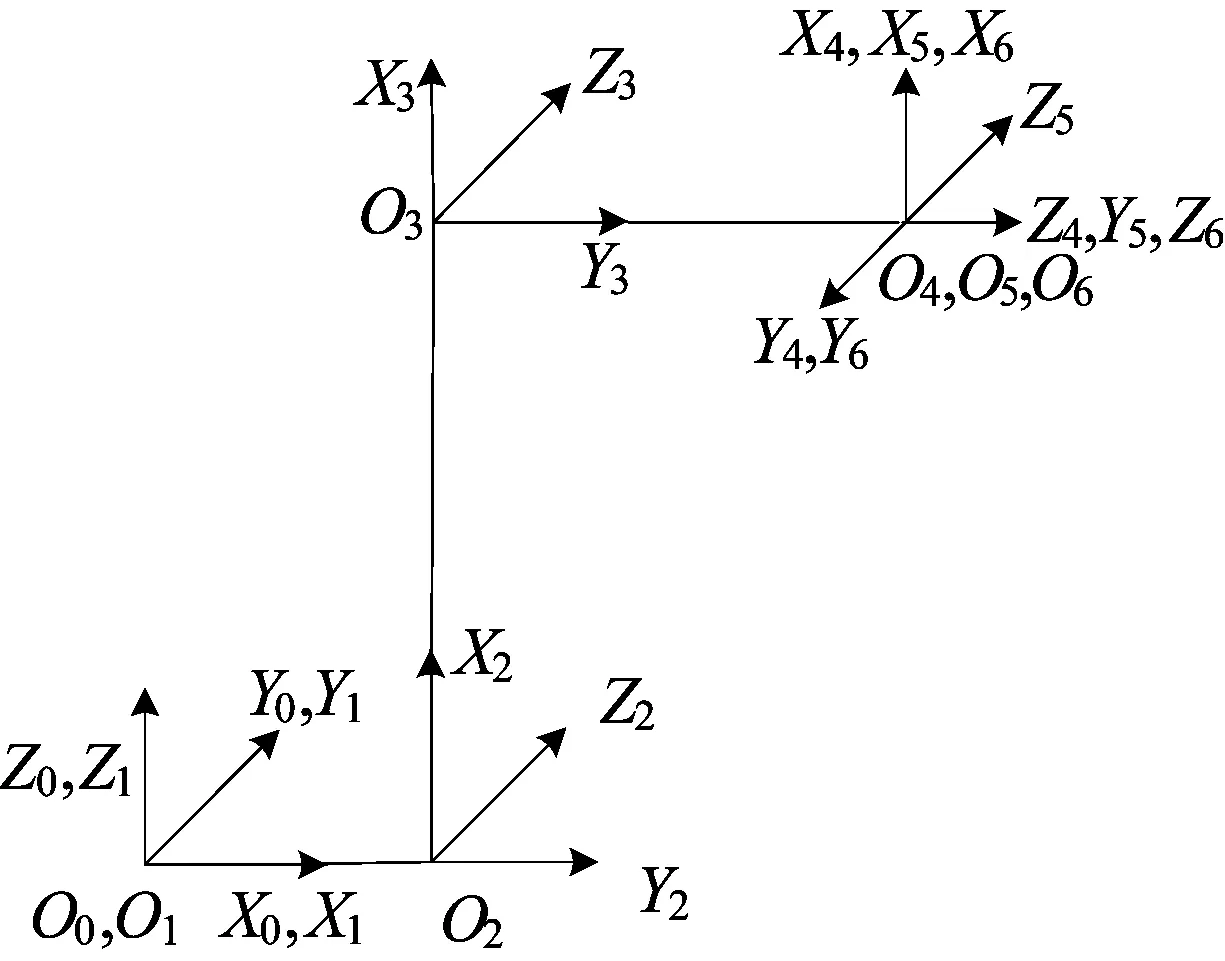
图1 IRB1600的连杆坐标系

表1中:αi-1为连杆扭转角,是相邻轴线在同一平面内的夹角;ai-1为连杆长度,是关节轴i-1与关节轴i之间公垂线的长度;di为连杆偏距,是沿2个相邻连杆公共轴线方向的距离;θi为关节转角变量,是两相邻连杆绕公共轴线旋转的夹角。则坐标系{i}相对于坐标系{i-1}的变换矩阵为:

(1)

(2)

其中:n、o、a为3个列向量,表示机械臂的姿态;p为机械臂末端的三维坐标。

2 碰撞检测

在实际工作环境中,障碍物多为不规则物体,建模难度高,本文采用长方体包络法简化障碍物,具体做法是将不规则的障碍物用体积最小的长方体包裹起来。

假设机械臂关节i和关节i+1处的坐标分别为Pi(xi,yi,zi) 和Pi+1(xi+1,yi+1,zi+1),则连杆li所处直线的方向为M=(xi+1-xi,yi+1-yi,zi+1-zi)。以长方体平行于x轴的上平面N为例,P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)、P4(x4,y4,z4)为上平面N上的4个顶点,通过计算可得到平面N的法向量K=(k1,k2,k3)。若K·M=0,则表示直线与平面N平行;若K·M≠0,则表示直线与平面N相交,必定存在交点P0(x0,y0,z0)。交点若为碰撞点需满足以下约束条件:首先交点在平面N的内部;其次交点处于连杆线段上。由以上约束可得到如下公式:

(3)

3 基本蚁群算法

蚁群算法在第1次迭代时通过启发信息寻找起始点到目标点的可行解并分泌信息素,之后的搜索过程又受到信息素的吸引,形成正反馈,逐渐找到全局最优目标并收敛。

3.1 状态转移概率

状态转移是指蚁群的移动,需要先计算蚂蚁的状态转移概率再按轮盘赌选择下一步前往的位置,公式如下:

(4)

其中:集合{allowed}为第k只蚂蚁下一步所能选择的路径节点集合;α为反映信息素在蚂蚁选择路径的相对重要程度的参数;β为反映启发式信息在蚂蚁选择路径的相对重要程度的参数;τij(t)为连接节点(i,j)之间的信息素浓度;ηij(t)为连接节点(i,j)上的启发函数,取为1/dij。

3.2 信息素的更新规则

信息素的更新是指量化人工蚂蚁在路径上分泌的信息素及进一步模拟自然界中信息素的挥发过程,公式如下:

(5)

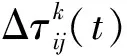
4 改进蚁群算法

基本蚁群算法有以下缺点:每个路径节点的初始信息素相同且启发值之间也不存在明显差异,因此致使蚁群盲目搜索,难以找到全局最优解。为了解决上述问题,本文进行如下改进:

考虑到障碍物的复杂程度和工作空间的大小,将蚁群进行划分,即

(6)

q=m-p

(7)

其中:p为外层蚁群数量;q为内层蚁群数量;Vobstacle为障碍物所占体积;Vworkspace为工作空间大小;m为蚂蚁总数量。

4.1 设置安全因子

根据机械臂能否安全到达,对三维空间内各离散点计算安全值,即

(8)

其中:Safe(Pi)为当前节点Pi搜索域内的安全点;Pi+1为待选节点;S为搜索区域内各离散点的安全因子。若离散点处于障碍物外且机械臂各连杆均未与障碍物发生碰撞,则将该点设为安全点,将其值设为1;否则将其值设为0。

4.2 外层蚁群启发函数设计

对于外层蚁群来说,需要在无初始信息素的前提下规划出合理路径,因此本文在设计外层蚁群启发函数时需考虑待选节点与目标节点距离的影响,其启发函数为:

(9)

其中:djg为当前计算的待选节点到目标节点的距离;min(djg)为所有待选节点到目标节点距离的最小值。

4.3 内层蚁群启发函数设计

鉴于A*算法寻路速度较快,其启发式成本由采用估价函数f(n)表示,通过f(n)来指导节点的扩展与搜索,每一次都是搜索从起点到终点之间使得f(n)最小的路径,估价函数方程为:

f(n)=g(n)+h(n)

(10)

其中:g(n)为从起点到当前节点的实际路径代价;h(n)为从当前节点到终点的预估路径代价。

因此,将A*算法的估价函数用作内层蚁群的启发式信息,以便于搜索全局最优路径,加快收敛速度;同时,将安全因子也添加到内层蚁群算法的启发函数中,改进后的启发函数为:

(11)

4.4 信息素不均匀分布

(12)

4.5 信息素更新规则的改进

为提升算法的收敛速度、获得最优路径,在更新蚁群信息素时引入狼群的猎物分配机制[14],狼群猎物分配机制的原理是在完成狩猎后,善于狩猎且身体强壮的狼会获得大量食物,而身体瘦弱的狼只能分得少量食物,这样整个狼群才能有更高的几率在下一次狩猎时捕获猎物,经过多次迭代,该狼群的生存能力逐渐被提高。因此,借鉴狼群的猎物分配机制改进信息素更新规则,最短路径上的信息素浓度会增加,同时最长路径上的信息素浓度降低,突出不同路径信息素的差异化,从而提高了蚂蚁中优质种群的生存能力,改进后的信息素更新公式为:

τij(t+1)=(1-ρ)τij(t)+

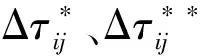
(13)

其中:Lbest、Lworst分别为每次蚁群到达目标节点的最优路径和最差路径;δ、ω分别为每次搜索时找到最优路径和最差路径的蚂蚁数量。

4.6 信息素浓度限制

经过上述改进,蚁群算法的收敛速度得到了提高,但会造成部分路径上的信息素浓度过高,进而降低算法对其他路径的选择,导致搜索出现停滞,为了防止这种情况产生,借鉴最大最小蚂蚁系统将信息素的浓度范围限定在τmin～τmax之间,具体公式为:

(14)

4.7 算法实现流程

(1) 初始化算法参数,设置起点和终点以及安全因子。

(2) 按(6)式和(7)式蚁群分为外层蚁群和内层蚁群,分别设计不同的启发函数。

(3) 先由外层蚁群在无信息素状态下进行搜索,将搜寻到的最优参考路径转化为初始信息素的强化值,由(12)式空间内各点信息素初始分布。

(4) 再由内层蚁群进行路径寻优,记录每次循环的最优路径。

(5) 按(13)式对信息素进行更新,并按(14)式限定信息素浓度范围。

(6) 判断循环次数是否达到最大值,若达到,则对搜索到的最优路径进行碰撞检测;否则跳转到步骤(4)。

(7) 若没有发生碰撞,则输出路径,结束;若发生碰撞,则跳转到步骤(3)。

算法实现流程如图2所示。

5 仿真分析

5.1 改进的蚁群算法规划路径的平稳性

本文使用MATLAB 2018a软件,在CPU为corei5-4210U,运行内存为8 GB的Win10计算机上进行实验。算法中各参数设置如下:α=1,β=5,ρ=0.9,Q=100,m=50,N=100。为验证使用本文改进的蚁群算法在不同复杂障碍环境下规划出的路径平稳性更好,分别使用本文改进蚁群算法、文献[12]算法以及基本蚁群算法,在如下3种复杂环境下模拟机械臂末端执行器进行路径规划。

路径规划结果如图3所示,在3种复杂度不同的环境下,使用本文改进蚁群算法均可以为机械臂规划出一条符合运动条件限制的避障路径,根据不同障碍物环境下规划的路径来看,使用本文改进的蚁群算法比文献[12]算法和基本蚁群算法规划出的路径拐点更少,而且搜索到的路径长度也相对优于其他2种算法。因此,使用本文改进的蚁群算法规划路径的平稳性要优于文献[12]算法和基本蚁群算法。

5.2 改进蚁群算法路径规划的高效性

为进一步验证本文对基本蚁群算法改进的高效性,在环境3的条件下,分别用本文改进的蚁群算法、文献[12]算法和基本蚁群算法模拟机械臂末端的运动规划路径,3种算法均进行20次仿真,统计结果见表2所列。3种算法处于最优路径长度的收敛曲线如图4所示。

表2 3种算法仿真20次结果统计

图4 3种算法最优路径收敛曲线

依据以上数据可知,使用本文改进蚁群算法模拟机械臂末端进行路径规划,比其他2种算法所得的平均路径代价更优,收敛速度也更快,且在多次仿真中规划出的路径稳定性更好,显著地提高机械臂在路径规划中的效率。

为进一步验证本文改进蚁群算法的可行性,使用RobotStudio软件中的IRB1600机械臂进行模拟实验,仿真过程如图5所示。

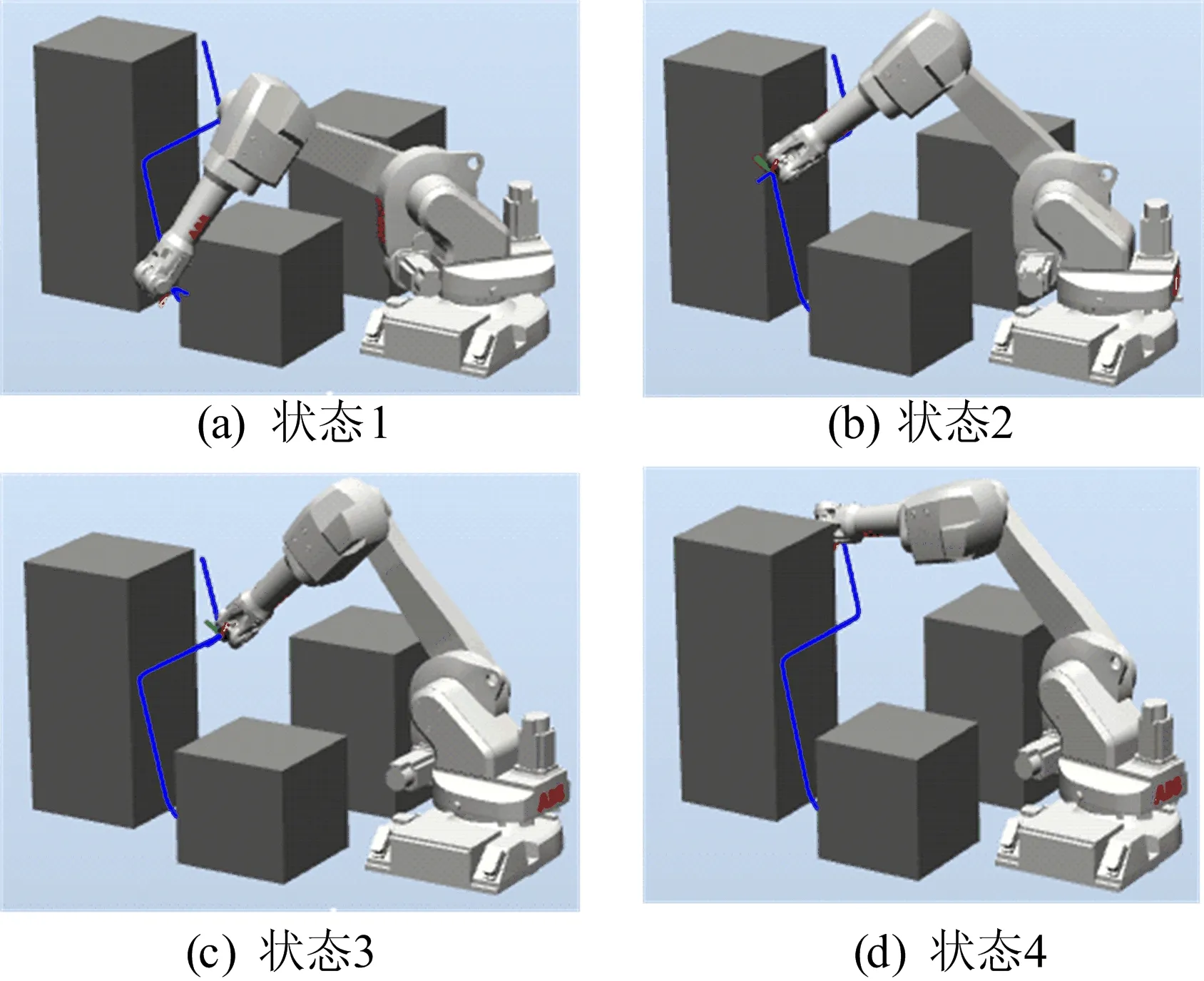
图5 机械臂避障仿真过程

由图5可知,机械臂本体未与障碍物发生接触,体现了本文碰撞检测算法的有效性。由以上仿真实验可知,使用本文改进的蚁群算法对机械臂进行路径规划时,能够为机械臂搜索到一条避免碰撞且能满足运动要求的路径。

6 结 论

针对蚁群算法在机械臂路径规划中存在的问题,如搜索路径过长、收敛速度慢等,本文对蚁群算法作如下改进:将蚁群分为外层蚁群和内层蚁群,分别设计不同的启发函数,并引入安全因子提高机械臂运动过程的安全性,利用外层蚁群初始化信息素,引导内层蚁群进行全局寻优,在更新信息素时引入狼群的猎物分配原则,限制部分路径信息素浓度于合理范围内。改进的算法通过在MATLAB和RobotStudio中的仿真验证,结果表明改进后的蚁群算法在收敛速度上,路径代价相比基本蚁群算法和文献[12]算法具有明显的优势,而且在机械臂仿真中表现良好,可以快速地为机械臂规划一条最优路径。