一种基于人工蜂群算法的多目标路径决策方法

侯 帅 关文玲 副教授 余钢杰

(天津理工大学 环境科学与安全工程学院,天津 300384)

0 引言

随着中国经济的快速发展,城市里的各类建筑逐渐增多,这些建筑大多内部结构复杂,通道树形交叉,路径复杂度较高,火灾疏散时需要大量绕行,而且这些建筑内可燃物种类多、数量大,极易发生大面积立体火灾,建筑内,尤其是人员密集的建筑内一旦发生火灾,扑救和人员疏散难度大,极易造成群死群伤的严重后果。因此,如何在火灾发生后将建筑内的人员安全地疏散出去是一个值得关注的问题。

规划应急疏散路径本质上可以看作是一个最短疏散路径问题,是求两节点间边的权重最小加和[1],学者已将多种算法应用于规划应急疏散路径中。例如,刘敏等[2]提出一种改进的量子蚁群算法用来优化疏散路径,在不需要强大处理资源的情况下,大量减少疏散时间;Kurdi等[3]通过引入平衡疏散算法,提出一种确保多出口情况下行人安全疏散的算法,解决疏散中的拥挤问题。然而,大多数研究都仅仅将疏散效率和拥挤度作为优化目标,忽略了火灾燃烧产物对人员的影响,因此,近年来许多学者将火灾风险和路径复杂度作为路径规划模型的优化目标。例如,Mirahadi等[4]基于火灾的位置与建筑结构的脆弱性定义每个房间的风险值,使用Dijkstra算法计算出最低风险路径;曹祥红等[5]提出一种用于火灾疏散路径动态规划的新型改进蚁群算法,并通过CO浓度、环境温度、拥挤度影响的当量距离改进启发函数,将逃生人员快速安全的指引向安全出口;巩慧等[6]结合实际场景信息,利用几何拓扑学方法对Dijkstra算法进行路径平滑度处理,降低路径复杂度,有效提升所规划路径的质量。

基于以上研究,本文将火灾风险、路径长度以及路径复杂度作为优化目标,旨在进一步提高火灾中人员疏散的安全性与效率。同时,Dijksra算法是使用最为广泛的算法之一[7],许多研究都将Dijkstra算法等传统算法应用在疏散领域。但Dijkstra算法和A*算法等传统算法并不适用于有多个终点的路网的路径规划问题,同时也不适用于解决一些较为复杂的数学模型,如A*算法每个节点的运算量大、时间长,随着节点数目的增加,算法搜索效率会降低,尤其是在面对复杂场景时,将很难规划出路径。人工蜂群算法(Artificial Bee Colony,ABC)是一种控制参数少、搜索效率高的种群算法,在解决更复杂的路径规划问题方面具有相当大的潜力,如Khamis等[8]提出基于随机方法的ABC算法对多房间布局的建筑出口位置进行优化,利用基于社会力模型的人群疏散模型避免人群密度过高,以实现疏散时间最小化。因此本文选用ABC算法对多目标模型求解,最终可得出同时考虑了火灾风险与疏散效率的最优疏散路径,保障逃生人员安全的同时大幅提高疏散效率,为人员疏散研究提供一些新思路。

1 疏散模型构建

1.1 应急疏散网络的构建

在逃生过程中,路径的选择是一个多目标的优化问题,需要权衡许多因素。从图论的角度来看,建筑物内错综复杂的通道形成一个连接的网络图,这里的通道被视为网络中的连接弧,通道之间的交叉点视为节点,连接弧代表节点之间的连接。定义应急疏散网络为无向图G(V,E) ,其中V为节点集合,E为弧线集合。定义v1,v2,…,vn为网络中的节点,即V={v1,v2,…,vn},其中vn为目的节点,vs为源节点;(vi,vj) 代表节点vi与节点vj之间的弧;Lij为节点vi和vj之间的实际距离。

1.2 逃逸代价的计算

窒息性气体和高温是火灾中的主要致命因素[9]。其中,一氧化碳(CO)是最主要的窒息性气体,甚至可能是受害者死亡的最主要原因[10]。火灾中的烟雾扩散开以后,会降低逃生路径中的可见度,延误逃生时间。人群过度拥挤也会增加逃生人员在火灾现场的停留时间,且会大幅增加踩踏事故的概率。这些风险因素随着火灾发展到一定程度后,会对人群造成巨大伤害甚至死亡,因此逃生人员有必要避开这些高危区域。本文设置关于风险因素的禁行阈值,模型将不会考虑风险因素达到禁行阈值的路径。通过查阅AcuteExposureGuidelineLevelsforSelectedAirborneChemicals,确定10min的AEGL-3标准值(1.7e-3mol/mol)作为CO的禁行阈值[11],在含有此浓度以上的CO环境中超过8min就会有生命危险;而温度的禁行阈值则是通过计算人体在不同温度下的最高耐受时间确定的[12],最终确定为120℃,人体在此环境温度下最大耐受时间只有7min;当人群密度≥4人/m2时,人与人之间的行走就会发生接触,出现停滞[13],因此关于拥挤度的禁行阈值设置为4人/m2;当减光系数大于1.2m-1时,周围环境几乎就是完全黑暗的,因此本文使用1.2m-1作为可见度的禁行阈值。体现在图论中,则是去除某风险因素超出禁行阈值的弧,利用剩下的网络结构搜寻最优路径。

当风险因素水平低于所设置的禁行阈值时,本文将讨论使用逃逸代价判断其对疏散效率的影响。在火灾中,单纯使用实际距离计算最短路径显然是不合理的,因此本文使用2节点间的逃逸代价作为计算依据,计算逃逸代价最小的路径。由于逃生时各通道内的人群密度变化较快,因此本文对于拥挤度这项风险因素的考虑是仅设立禁行阈值,而不将其作为逃逸代价参考的依据。结合火灾的动态扩散影响,加入权重修正因子,将传统的物理距离转为疏散逃逸代价:

(1)

式中:

Wij—人员从vi到vj所需要付出的逃逸代价,受路径的长度和风险水平影响;

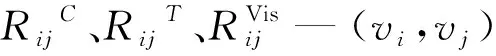
权重修正因子α1,α2,α3∈[0,1],且α1+α2+α3=1,这些修正因子分别代表CO浓度、温度和可见度在Rij中的相对重要程度。

基于前人研究,根据不同温度、CO浓度水平下试验得出的人体忍耐时间数据[14],提出逃逸代价系数RijC、RijT的量化方式。因温度和CO浓度分别在40℃和1e-4mol/mol时开始明显影响人体行动,将该2项数值作为各疏散影响量化研究的起点,低于这个水平的温度和CO浓度将被视为可接受风险,在逃逸代价系数中体现为0。用Matlab软件进行Logistic曲线拟合,同时为了所得值更加同质化而进行特殊处理,得出了新的RijC、RijT的量化方式。

(2)

(3)

式中:

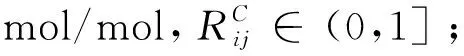
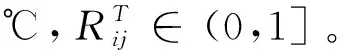
在Jin等[15]实验中,在减光系数小于0.35m-1时,烟雾对人员行动速度几乎没有影响;随着减光系数的增大,人员的行走速度逐渐变慢;当减光系数大于1.2m-1时,人们不得不在黑暗的环境中用手沿着墙壁行走。Jin将无刺激烟气的减光系数值与对应的人员步行速度值拟合,得到减光系数对人员行动速度的影响系数表达式,本文参考此关系式,将其转换为减光系数与疏散代价系数之间的关系,见公式(4)。其中KC为减光系数。

(4)

1.3 单目标路径规划模型

本文中的逃逸代价受路径长度与路径中的风险水平影响,逃逸代价最小的路径在一定程度上兼顾疏散安全性与效率,为逃生人员选择最小逃逸代价路径的ModelⅠ如下所示。

(5)

S.t

(6)

(7)

xij=0,1,i=1,2,…,n,j=1,2,…,n

(8)

式中:

f1—所选疏散路径的逃逸代价;

F1—所有疏散路径中最小的逃逸代价;

xij—模型中的决策变量,当(vi,vj)包含在疏散路线中时,xij=1;当(vi,vj)不包含在疏散路线中时,xij=0。

式(5)是ModelⅠ的总目标,即选择逃逸代价最小的路径;式(6)通过限制xij的值来保证路径的可行性;式(7)可以避免路径中存在循环路径;式(8)是决策变量xij的数值约束。

研究表明,在应急网络中,大多数的拥挤和恐慌都发生在弧的交叉处[16],即路径交叉处。路径的复杂度可以表达为所选择的疏散路径中包含弧的数量,所含弧的数量越少,所需要经过的路段也就越少,则路径复杂度越低。考虑路径复杂度的ModelⅡ可以表达如下:

(9)

S.t．

(5)—(8)

式中:

f2—所选疏散路径的复杂度;

F2—所有疏散路径中最低的路径复杂度。

1.4 多目标路径规划模型

解决多目标问题的常用手段是加权法,转换为一个单目标问题进行研究。实际上,加权法和理想点法都可以有效地求解多目标非线性问题的Pareto最优解,本文使用加权理想点法来处理多目标问题。Pareto最优解可以通过下面的ModelⅢ得到。

(10)

式中:

F—关于逃逸代价和路径复杂度的综合动态权值;

γ1、γ2—逃逸代价和路径复杂度的权重修正因子,分别表示逃逸代价和路径复杂度的相对重要程度,γ1≥0,γ2≥0,γ1+γ2=1,γ1和γ2变化,f1和f2也会出现相应的递增或递减;

2 人工蜂群算法求解模型

人工蜂群算法将蜂群分为采蜜蜂、观察蜂和侦查蜂,每一次搜索过程中采蜜蜂和观察蜂先后开采蜜源,即寻找最优解,而侦查蜂则观察是否陷入局部最优,若陷入局部最优则随机搜索其他可能的蜜源。求解ModelⅢ的人工蜂群算法如下:

(1)算法参数初始化。随机生成SN个蜜源(等于采蜜蜂的数量),参数limit初始为0,迭代终止次数为1。随机产生某个蜜源的公式如下:

vxy=vmin,y+rand(0,1)(vmax,y-vmin,y)

(11)

式中:

vxy—第x个蜜源的第y维度值,x∈{1,2,…,SN},y∈{1,2,…,D};D代表最高维度值。

vmax,y、vmin,y—第y维的最大值和最小值。

(2)计算蜜源适应度。人工蜂群算法一般通过较大的适应度值指引算法向全局最优化,fx是待解问题的目标函数值,适应度函数用公式(12)表示:

(12)

适应度可以理解为优化问题的目标函数,本文的适应度函数设计为:

(13)

(3)重复以下步骤,直到满足终止条件。

(4)新蜜源的更新搜索。采蜜蜂记录当前最优的适应度值,并在当前蜜源的邻域内展开搜索,搜索新蜜源的公式为:

(14)

式中:

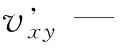
vk—邻域蜜源,k∈{1,2,…,SN},且k≠x;

φxy—[0,1]之间的随机数。

得到新蜜源以后,根据贪婪算法,比较新旧蜜源的适应度值,选择优者。

(5)当所有的采蜜蜂完成搜索以后,会把解的信息fitx与观察蜂分享。观察蜂根据概率Px(轮盘赌法)选择跟随的采蜜蜂。

(15)

观察蜂开采过程与采蜜蜂一样,利用式(14)寻找新蜜源,并保留适应度值更优者。每个蜜源拥有参数limit,当蜜源更新被保留时,limit+1;反之,limit不变。因此limit可以统计出某个蜜源被更新的次数。如果某蜜源的参数limit=10时,那么就认为该解陷入局部最优,该蜜源就会被舍弃,该蜜源对应的观察蜂转变为侦查蜂,通过式(11)随机产生一个新蜜源代替原蜜源。

3 实例分析

该算法可根据火势蔓延动态调整和优化路线,为了验证所提出的算法,设计以下案例进行研究。完成火灾模拟软件Pyrosim中建筑模型搭建后,得出某建筑结构图,如图1。在其内部的通道内均匀地布置CO、温度采集器,鉴于人群的平均高度,采集器的检测高度设置为1.6m。起火点设置于通道交叉处,进行模拟后得到整个火灾过程中CO质量浓度、温度、能见度随时间变化的数据。

图1 某建筑结构示意图Fig.1 Schematic diagram of a building structure

建立应急疏散网络模型,节点3、20为目的节点,以节点19为例寻找最优逃生路线(图2中以深色线条代表)。从图2(a)可以看出,在没有火灾影响的情况下,节点19的最优逃生路线为19→11→4→5→6→3。运行火灾动力学模拟工具(Fire Dynamics Simulator,FDS),加载火灾数据后,路线11→4的危险性增加,路线4→5达到禁用标准,使用ABC算法重新规划最优路线,如图2(b)。节点19的最优逃生路线由19→11→4→5→6→3改为19→11→12→7→8→9→6→3,避开了危险路线11→4→5。随着火势的蔓延,不可用的通道增多。如图2(d)所示,火灾发生120S后,路线再次发生变化,节点19的最优逃生路线改为19→11→12→7→8→13→14→17→16→20。这验证了所提出的路径优化算法用于考虑火灾蔓延对疏散路线影响的可行性。

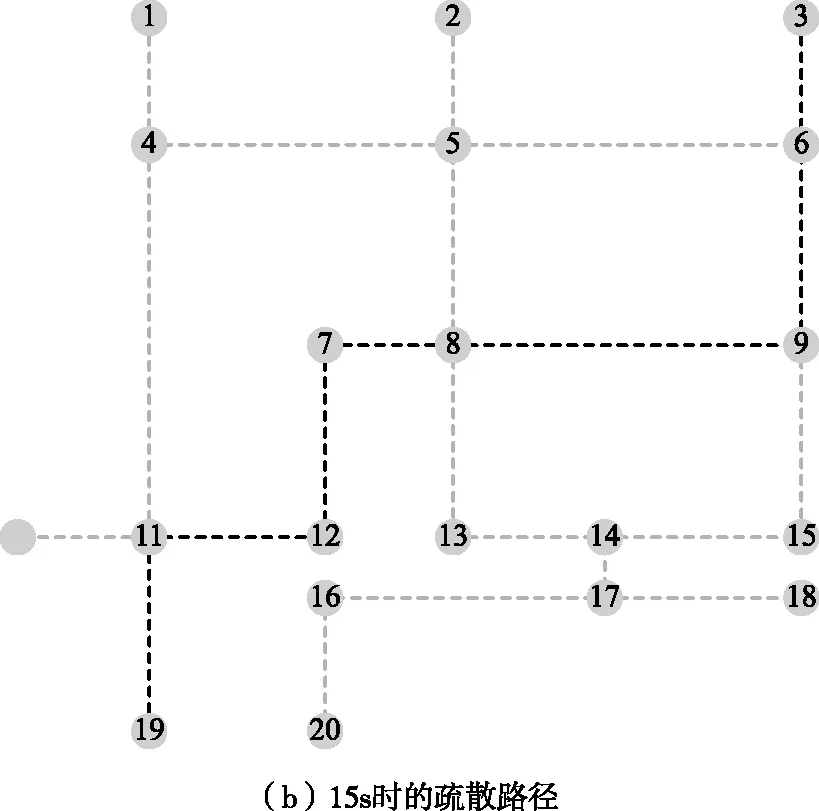
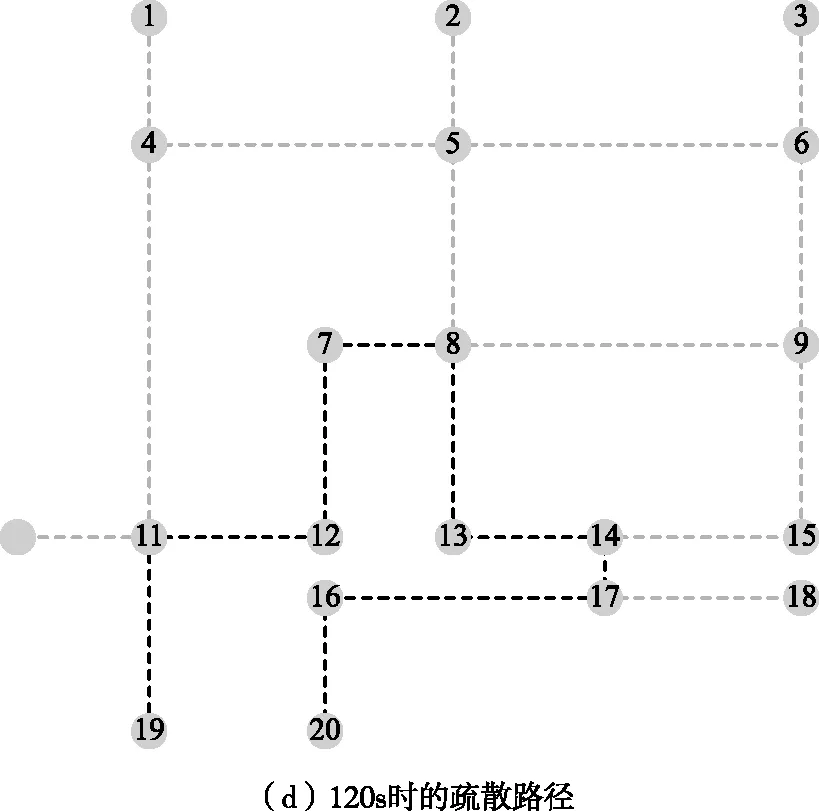
图2 随时间变化的最优疏散路线Fig.2 Optimal evacuation routes over time

4 结论

本文从应急人员疏散的角度出发,以疏散过程中的安全及效率为目标,提出一种考虑逃逸代价和路径复杂度的多目标路径规划模型,并利用ABC算法对模型进行求解。最后以某建筑作为案例进行研究,在Pyrosim中搭建模型,得出最优疏散路径。可以发现,得出的最优疏散路径可以很大程度上避免火灾的侵害,随着烟气的扩散,相应的最优路径也在动态调整。同时,风险因素水平达到禁行阈值的路径将不会被考虑,在很大程度上保障了人员的生命安全。

但是本文所考虑的风险因素并非全面,例如没有对人员参数进行考虑。人具有主观能动性,复杂的火灾现场情况多变,人员疏散需要对人员构成、人员数据以及恐慌心理等因素进行考虑,这也是未来需要进行的下一步工作。