基于Tsallis熵的两点法确定明渠断面流速分布及数值模拟验证

唐皓东，周义仁

（太原理工大学水利科学与工程学院，太原 030024）

0 引 言

迄今为止，中外研究者对明渠紊流流速分布进行了大量的研究与实验，提出了众多描述明渠流速分布的方法与公式。Knelegne将平板边界层理论应用到明渠流，得到明渠流动对数流速分布规律，并给出对数率公式[1]，虽然能够近似的表示流速分布，但无法描述横断面最大流速位于水面下的情况；Coles在明渠中引入尾流函数概念，采用对数和尾流律的线性组合来确定明渠流速分布[2]，Nezu等研究了光滑壁面水槽均匀紊流，认为粘性底层内的流速为线性分布，过渡区外的流速为对数公式和尾流律[3]，但直至今日，对公式中尾流强度系数的取值没有一致的结论；孙东坡通过分析矩形明渠流速分布理论，建立了明渠沿垂线流速的分布公式和沿横向流速的乘幂函数分布公式[4]，虽然整体流速曲线较对数率更加准确，但靠近渠底部分精度不高；胡云进利用三维紊流数学模型在多种工况下进行试验，得出明渠底部内区和明渠外区，分别符合对数分布定律和抛物线分布的结论[5]，但在水面和渠底附近仍有较大误差。上述这些公式存在泛用性较差的缺点，涉及参数较多导致计算结果存在较大误差，在需要精确计算断面流速时难以应用。

随着信息熵的不断发展，有学者将熵的概念引入明渠流动中，提出基于熵的流速分布公式。Chiu引入香农熵的概念，以熵为基础应用最大熵原理推导出明渠断面流速分布公式，该流速公式能够描述纵向最大流速发生在水面或水面下时的垂向和横向流速变化[6,7]；Moramarco通过将一维分布应用于二维截面中的每个垂直剖面，得到二维速度分布[8]；Moramarco和Singh研究表明平均流速和最大流速确定的熵参数为常数，不依赖于水流流态，只与渠道形状、糙率等几何特性有关[9]；Luo和Singh提出用Tsasllis熵替代Shannon熵推导明渠流速分布，并得到基于Tsallis熵的流速分布公式[10]；Cui和Singh使用标准x-y坐标系，得到二维速度分布方程，应用非线性方程计算累计概率分布，推导出基于Tsallis熵的明渠二维流速分布[11,12]。虽然基于熵的流速公式能够表示断面流速分布，但公式中熵参数的计算需要利用河道历史测量资料，具有较大的局限性，本文基于Luo和Cui等人关于Tsallis熵的流速分布的研究，对熵参数G进行推导得到广义熵参数Gp，进一步提出两点法确定断面横纵向流速分布的方法，弥补了Tsallis熵流速公式在没有历史测量资料时无法应用式的缺点。

1 基于Tsallis熵的明渠二维流速分布公式的推导

Tsallis熵推导明渠流速分布需要以下几个步骤：①引入Tsallis熵；②确定速度累计分布函数；③确定约束条件和最大熵原理；④纵向流速分布的推导；⑤横向流速分布的推导；⑥计算断面最大流速。

1.1 Tsallis熵

将渠道横截面顺水流方向时间平均流速u看作随机变量，u为横截面任意一点的速度值，f(u)是速度u的概率密度函数，umax为截面最大速度，速度分布的Tsallis熵H可以写作[10]：

式中：m为实数；当m＞0，H(u)是个凸函数。u的取值范围为0～umax，f(u)的取值范围为0～1。

1.2 速度的累计分布函数

由于边界条件等因素的影响，明渠紊流常伴随有和主流方向垂直的横向环流，也称为二次流[13]，在二次流影响下，明渠最大流速可能发生在水面以下，这种现象称为dip现象[14]，越靠近边壁的位置最大流速越远离水面，这种现象在河道中普遍存在。为了更好的表示明渠二维流速分布，Chiu建立与y-z坐标系相关的r-s坐标系[6]，如图1所示，其中r与速度值有唯一的一一对应关系，曲线s则是曲线r的正交轨迹。时间平均速度由u表示，速度沿等值线无变化，流速最小的壁面流速值趋于零，对应于r等于r0的值，速度最大值由umax表示，对应于r等于rmax，umax可能出现在水面或水面下。速度u随空间坐标r从r0到rmax的变化而单调增大，但不一定随河床高度y的变化而单调增大。图中h表征截面几何结构的系数，h的取值范围为-D＜h＜+∞，当断面宽深比较大时，h＞0，h没有任何物理意义，它只是一个有助于形成图1等压线模式坐标系的系数，umax出现在水面；当断面宽深比较小时，h＜0，|h|代表水面下umax的实际深度。如果h非常大，等压线是平行的水平线，此时速度仅随y变化，r接近y∕D，这种情况往往发生在宽深比较大的渠道中。

图1 速度分布与曲线坐标系Fig.1 Velocity distribution and curvilinear coordinate system

Chiu将横截面中速度的累计概率分布表示为：

则概率密度函数表示为：

为了用y和z坐标表示二维速度分布，chiu和chiou推导出了一组从r-s坐标到y-z坐标的表达式[15]：

当h≤0：

当h＞0：

Yang等人[14]提出用矩形明渠流速分布的倾角修正测量定律来描述dip现象，公式为：

式中：ymax表示断面最大流速到河床的距离；D表示断面水深；α表示倾斜修正系数；z表示流速点距离边壁的距离。

对河道中心线z=b，则，由此可以推导出：

1.3 约束条件和最大熵原理

根据最大熵原理，水流稳定时，流速的概率分布趋于熵最大，可以利用最大熵原理选择f(u)。需要从观测的流动中得到有关流动特性的约束条件，自然渠道流动中需要满足质量、动量、能量守恒定律，这些定律可以用来构造约束条件，为了得到速度分布，需要应用质量守恒，总概率和质量守恒的约束条件表示为：

式中：um是横截面平均速度，等于Q∕A，这里的Q是过水断面流量，A是过水断面面积。

基于上述两个约束条件构建Tsallis熵H的拉格朗日函数L，其中λ0和λ1是拉格朗日乘子。

方程L对f(u)求偏导：

得到速度的最小偏差概率密度函数f(u)[10]：

1.4 纵向流速分布的推导

由式（14）进一步推导：

计算拉格朗日乘子λ1和λV的方法很困难，在Chiu的速度方法中，定义了熵参数M[6]，以降低计算难度，它也可以作为表征和比较各种速度分布模式的指标。Moramarco的研究表明，熵参数M与河段的曼宁糙率系数、水力半径、宽深比等水力和几何特性有直接关系[9]，因此使用熵参数时不需要再重复考虑这些参数对水流的影响。在熵参数M的基础上，Cui提出的熵参数G[16]也具有同样的性质，可以通过以下方式定义：

经过研究实测资料，确定G符合以下公式：

则渠道横截面纵向流速u的表达式可以表示为：

对于同一渠道，参数G值和m值不随过水断面流量变化而变化，因此同一渠道中可确定一组G、m参数来表示断面流速分布情况[17]。

1.5 横向流速分布推导

从r-s坐标系可以看出，熵的理论不仅适用于纵向流速分布，也同样适用于横截面横向流速分布的推导。不同于纵向流速分布公式，横向流速分布公式需要重新确定的G与m值。结合公式（4），同一水深时流速最大值出现在渠道中心线，则累计概率分布公式Fp(u)可表示为：

式中：z为流速点距离渠道边壁的距离；b为渠道边壁到渠道中心线的距离。

在纵向流速分布中，同一断面不同流量下使用相同的熵参数G，而在横向流速分布中需要重新定义熵参数，um与umax的比值有较大的取值范围，因此可对G进行推广，对任意小于1的两个速度比均满足G函数。则通过公式（17）推导出广义熵参数Gp的取值：

式中：uz为横向流速曲线的任一点速度值；uc为与uz同一水深渠道中心线处的速度值；Gp为广义熵参数。

根据对称性原则，容易得到渠道横截面横向流速up的表达式：

通过测量已知uz，取up=uz可求得与Gp相对应的mp。

1.6 确定断面最大流速

已知流速uc与其相对水深y、最大流速点的位置h，带入公式（2）～（5）可计算出F(uc)，并通过简单验证可知，Gp、mp同样满足纵向流速分布公式，可求得断面最大流速公式：

结合计算结果可得纵向流速分布公式。

在Cui的推导的纵向流速分布函数中，熵参数G通过断面平均流速um和最大流速umax计算得到，m值根据经验取值为3，但该m值并不能广泛地应用在不同渠道中，在无历史实测资料的渠道中无法应用，而新推导的Gp、mp可以通过少量实测资料进行确定，大大简化了测量过程。

本研究将通过两点法推导并验证矩形渠道断面的横纵流速分布情况。由于实测时水流流速波动范围大，难以准确测量，且靠近边壁时流速测量困难，断面各点流速测量不完整，无法准确地描述横断面流速分布，而数值模拟软件能够精确计算不同工况渠道各点流速值，能更好地分析断面流速分布。因此，本文先通过实测资料验证数值模型的可靠性，再使用模型的模拟流速与基于Tsallis熵的流速公式计算流速进行对比分析，验证基于Tsallis熵流速公式的准确性。

2 数学模型介绍

2.1 控制方程及紊流模型

明渠流动属于三维不可压缩流动，基于连续方程和动量方程：

式中：ρ为流体密度；p为修正的压力；ui、uj为流速分量，i=1,2,3、j=1,2,3；xi、xj为坐标分量。

明渠水流基本为紊流，本文用雷诺时均（RANS）的数值模拟方法求解时均N-S方程组。明渠流动受到二次流的影响较大，为降低数值模拟的计算误差，研究采用RNGk-ε双方程模型对雷诺方程组进行封闭，湍动能k输运方程和湍动耗散率ε输运方程如下：

式中：μ为分子黏性系数；μt为紊流黏性系数，它的表达式为：，其中Cμ为经验常数，Cμ=0.084 5；Gk为由平均速度梯度引起的湍动能产生项；其中η0=4.377，β=0.012；常数αk=αε=1.39，C1ε=1.42，C2ε=1.68。

2.2 计算网格与网格无关性验证

建立宽0.27 m，高0.3 m，长15 m的矩形渠道模型，利用ICME CFD前处理软件对渠道模型进行网格划分，水流在渠道壁面附近存在边界层，需要对边界层区域进行网格加密。为避免计算过程中网格疏密程度对计算结果造成影响，对计算区域的网格进行了网格无关性验证。分别采用20万网格、30万网格、40万网格对渠道进行了模拟，以实现对网格的无关性验证。对3种网格模拟时采用的方法均相同，待计算稳定后，比较距离进水口10 m位置的断面的中心线流速分布曲线，在保证模拟精度的同时尽可能减少网格数量，确定最优网格尺寸，减轻计算量，计算结果如图2所示。

由图2可知，20万网格与后两种网格数量计算结果有明显差异，可以认为当计算网格数达到30万时，就能够满足网格无关性要求。因此在对不同工况下模拟明渠流动时均采用30万网格，此时，边界层第一层网格取0.001 m，增长速度为1.2，网格数量总计30 767个。

2.3 边界条件和数值方法

采用有限体积法对控制方程进行离散，速度压力耦合采用SIMPLE算法，湍动能和湍动能耗散率的离散格式均采用二阶迎风格式，其他项离散均采用QUICK格式。进口边界设为速度进口，上边界和出口边界为压力出口；壁面边界采用标准壁面函数法处理边界；计算残差设为10-6，计算步长设0.005 s。

自由液面的模拟采用VOF模型，该模型是一种表面跟踪技术，主要应用在各相不混溶的情况，各相流体共享动量方程，通过相分数描述各相。利用VOF模型可以准确得到明渠水流的水气交界面。

2.4 模型验证

为验证数学模型的可靠性，在实验室对矩形渠道进行了实测对比分析。测流实验在水流大厅矩形渠道中进行，光滑矩形渠道长15 m，宽0.27 m，高0.3 m。实验时通过阀门控制不同的来水流量，为保证边界层充分发展并形成均匀流，在水槽进出口布置多孔板减少水面波动，并选取进水口后10 m处为测量断面。实验渠道在流量为0.072 9 m3∕s的工况下流动平稳，本实验选用该流量作为参考进行计算，分别测量同一断面z∕b=0.4和z∕b=1的两条竖线上四点的流速情况，与模拟流速进行对比，如表1所示。

表1 Q=0.072 9 m3/s时流速计算值与实测值对比Tab.1 Q = 0.072 9 m3·s-1 flow velocity calculation value and the measured value comparison

由表1中8组流速关系对比，流速实测值和模拟值之间的平均误差均在±2%以内，表明该数学模型和选用参数有较高的模拟精度，可以认为该模型模拟的参数真实可靠。

3 结果分析

由式（20）可知，任意水深的两测量点流速分别为uz和uc，可求得广义熵参数Gp，已知uz所在位置，则通过公式（19）计算出Fp(uz)的值，将uz、uc、Gp和Fp(uz)带入公式（21），计算得到mp的值，由此确定横向流速公式；将uc和F(uc)带入公式（18），可计算出断面最大流速umax，确定断面中心线流速公式。

通过计算结果分析同一深度z∕b和G的关系，如图3所示，当z∕b＞0.5时，Gp值逐渐趋近于最大值，由流速分布情况可知此时uz∕uc趋近于1，使得mp值的计算结果趋近于1，无法正确得到横向流速分布，因此，通过两点法确定渠道断面流速分布时，第一点选取渠道中点，第二点选取0＜z∕b＜0.5范围内的任意一点。

图3 同一水深位置z∕b与Gp的关系Fig.3 Relationship between z∕b and Gp at the same water depth

在实测流量为0.072 9 m3∕s时，渠道水深为0.223 m，断面最大流速umax=1.41 m∕s，以相对水深y∕D=0.476为例，此时中心点流速uc=1.4 m∕s。

当0.5＜z∕b＜1时，同一水深不同测点流速相差过小，使得计算存在较大误差，因此选用0＜z∕b＜0.5范围内的流速测量值进行计算。断面中心位置从壁面到中心线流速变化更明显，因此选用y∕D=0.476作为测量水深。计算不同z∕b条件下的参数Gp，mp和断面最大流速umax计算，如表2所示。

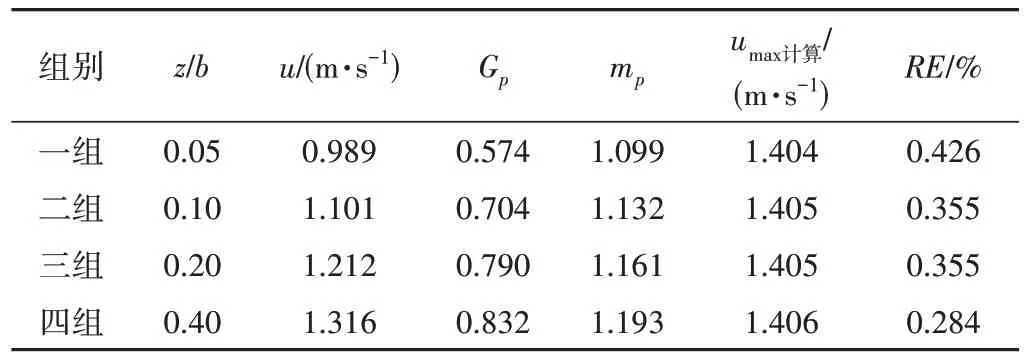
表2 相对水深为y∕D=0.476时不同z∕b条件下Gp、mp、umax计算计算结果Tab.2 Calculation results of Gp, mp and umax计算 under different z∕b when relative water depth is y∕D=0.476

图4、图5为分别利用1～4组流速点得到的流速分布图像，结果表明，在同一水深位置，取与边壁距离不同的两点测量流速，求得的Gp，mp均满足横向流速公式，由公式（21）可计算出横向不同位置的流速。各组计算的最大流速误差均小于±1%，即得到的两个参数同样适用于纵向流速公式。

图4 相对水深为y∕D=0.476时各组计算的横向流速分布图Fig.4 The transverse velocity distribution of each group when the relative water depth is y/D=0.476

图5 相对水深为y∕D=0.476时各组计算的断面中心线流速分布图Fig.5 The velocity distribution of the center line of the section calculated by each group when the relative water depth is y/D=0.476

取z∕b=0.484位置的纵向流速分布，计算不同相对水深y∕D条件下的参数Gp，mp和断面最大流速umax计算，如表3所示。

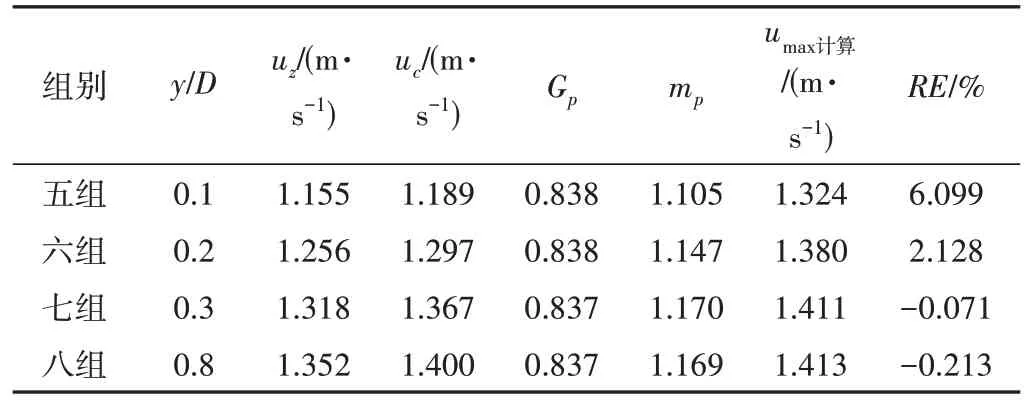
表3 z∕b=0.484时不同相对水深y∕D条件下Gp、mp、umax计算计算结果Tab.3 Calculation results of Gp, mp, umax计算 at different relative water depths y∕D when z∕b = 0.484

图6、图7为分别利用5～8组流速点得到的流速分布图像。图6表明，在与边壁距离相同但水深不同的位置取两点测流速，求得的Gp，mp均满足横向流速公式。图7表明，在计算纵向流速时，当相对水深y∕D＜0.3时，中心点流速过小，无法正确计算出断面最大流速，计算结果存在较大误差，当相对水深y∕D＞0.3时，计算结果有较高的精度。

图6 z∕b=0.484时各组计算的横向流速分布图Fig.6 The transverse velocity distribution of each group when z∕b=0.484

图7 z∕b=0.484时各组计算的断面中心线流速分布图Fig.7 The velocity distribution of the center line of the section calculated by each group when z∕b = 0.484

综上所述，两点法推算矩形渠道流速分布有着较高的准确度，满足灌溉渠道精确测量要求，新建立的r-s坐标系不受矩形边壁形状的制约，对于到梯形、U型等渠道也同样适用，因此，本文推导的流速公式广泛适用于各类灌溉渠道。

4 结 论

（1）本文通过讨论Tsallis熵在明渠流速分布上的应用，分析了明渠流速分布，对参数G和m进行了进一步推导，提出广义熵参数Gp，并利用实测资料推算出Gp与对应的mp，提出确定断面流速分布的新方法，通过实测资料和数值模拟验证，结果符合预期。

（2）利用Gp替代G，提高了流速公式的应用范围，解决了熵参数G只能通过断面平均流速和最大流速的比值确定的缺点，使得在无断面历史实测资料的情况下，可通过两点法确定参数值，得到断面流速分布情况。

（3）当0＜z∕b＜0.5时，同一水深下包括中心点在内的两点流速可计算出参数Gp和mp的值，能够准确表示断面横向流速分布。当0.3＜y∕D＜1时，通过横向两点流速计算的参数均能正确表示渠道中心线流速分布。