注意力机制和CNN结合的雷达辐射源个体识别
杨海宇,郭文普,康 凯,何婧媛,2,边 强
(1.火箭军工程大学 作战保障学院, 西安 710025;2.延安大学 数学与计算机科学学院, 陕西 延安 716000)
0 引言
辐射源个体识别(special emitter identification,SEI)是一项重要的电子情报活动,目的是利用与之相关联的脉冲无意调制(unintentional modulation on pulse,UMOP)识别雷达辐射源个体[1]。这一目的是通过精确测量雷达发射机硬件制造差异对雷达个体影响来实现的。不同辐射源之间的特征可用于识别雷达个体,并区分同一类型同一批次的雷达辐射源个体,称为雷达辐射源个体识别[2]。
在文献[3]中,孙德刚等人使用辐射源的瞬态信号进行特征提取,他们认为瞬态信号对SEI通常有特殊的射频指纹,因为当发射机打开或关闭过程中,信号被瞬时状态影响,如功率放大器的非线性特性导致UMOP。虽然这种方法是可行的,但准确地检测其瞬态信号是困难的,特别是在非合作通信中,瞬态特性很容易受到非理想和复杂信道条件的影响,难以捕获[4]。此外,瞬态信号对具有相同型号和同一批次的发射机识别性能较差[5]。文献[6]提出基于时域瞬态信号的雷达辐射源识别方法,引入了多层雷达辐射源识别概念,包括雷达功能识别、模型识别和特定辐射源识别,达到了较好的识别效果,但是建模的计算成本较大。然而,与瞬态信号相比,稳态信号的使用提供了更稳定的射频指纹特性。文献[7-10]提供另外一种研究思路,将稳态信号转换到其他信号域,如利用小波变换、希尔伯特-黄变换和双谱分析等方法提取出独特且稳定的指纹特征进行个体识别。然而,基于小波变换的识别算法难度在于小波函数的选取,基于双谱和希尔伯特-黄变换的个体识别方法均存在高维特征问题,徐书华[7]提出了基于局部积分双谱的个体识别技术,张静雯[9]提出了基于希尔伯特-黄变换的个体识别技术,但只是解决了从高维到低维特征的问题,缺乏对信号指纹特征提取。文献[11]提出了一种环线积分双谱(surrounding-line integral bispectrum,SIB)方法提取无意相位调制特征的方法。文献[12]提出了一种新的雷达SEI方法,该方法对采集到的雷达脉冲进行精确的时间对准和相干积分,以提高信噪比,从而有效地识别信号上的UMOP,使用基于变分模态分解技术提取与UMOP相关的特征。所提出的技术在真实雷达数据集上得到了较好的验证,但计算复杂度较高,所需时间较长。
近些年,深度学习在辐射源个体识别方面起到显著效果。文献[13]使用原始同相/正交(in-phase/quadrature,I/Q)数据作为卷积神经网络(convolutional neural network,CNN)输入,提出的方法省去预处理过程,较为高效。文献[14]提出了一种识别发射器的方法,使用CNN来估计每个发射器的I/Q不平衡参数。潘祎伟[15]构建了一个深度残差网络来学习希尔伯特谱图像中反映的视觉差异,有效地解决了退化问题,提高了效率和泛化能力。龚佳亮等[16]提出了一种基于信息最大化生成对抗算法,解决了未标记数据集的监督和半监督方法不兼容问题。文献[17]提出了一种基于压缩双谱和CNN(compressed bispectrum CNN,CB-CNN)的特定辐射源识别算法,利用压缩双谱法预处理原始信号,识别结果具有更高的精度。刘高辉等[18]利用深度置信网络识别分类通信辐射源个体,识别率仅达到80%。文献[19]使用一维时间序列信号训练3层长短期记忆(long short-term memory,LSTM)网络,简化了预处理过程。曲凌志等[20]提出一种结合双层注意力机制(attention mechanism,AM)和残差网络的通信辐射源个体识别方法,和残差神经网络相比,效果明显提升。文献[21]提出了一种使用双谱-拉东变换和混合深度模型(bispectrum-radon transform hybrid deep model,BRT-HDM)的方法,所提出的BRT特征在表示UMOP方面优于传统特征。文献[22]提出了一种基于脉冲图像和CNN(pulse waveform images CNN,PWI-CNN)的方法,PWI实现了将时域波形转换为二维图像,该方法在识别截获雷达脉冲信号中调制样式不确定的雷达个体方面优于现有方法。总的来说,现有方法在解决雷达辐射源个体识别问题上,抗噪性能、识别准确率和识别速度有待提高。
为解决雷达辐射源个体识别准确率低、抗噪性能差、训练时间长的问题,本文提出一种注意力机制和卷积神经网络(attention mechanism convolutional neural network,AM-CNN)结合的雷达辐射源个体识别算法,将自我注意力机制模块引入CNN网络,虽然AM-CNN算法在其他领域有着广泛应用,但是该算法在雷达辐射源个体识别领域相比于其他算法有着更为显著的效果,AM-CNN算法既能保留CNN网络的深层特征提取性能,又能检测与个体识别关联性更强的特征,可以有效解决雷达辐射源个体识别问题。
1 基本理论
1.1 系统模型
雷达发射机的任务是为雷达系统提供一种满足特定要求的大功率射率发射信号,经过馈线和收发开关并由天线辐射到空间。通常分为脉冲调制发射机和连续波发射机。这里主要围绕常用的主振放大式发射机展开分析。主振放大式发射机的组成如图1所示,主要由射频放大链、脉冲调制器、固态频率源及高压电源等组成。对于脉冲雷达而言,在定时脉冲的作用下,各级功率放大器受对应的脉冲调制器控制,将频率源送来的发射激励信号进行放大,最后输出大功率的射频脉冲信号[23]。

图1 主振放大式发射机的组成Fig.1 Composition of main vibration amplification transmitter
功率放大器是发射器主要硬件之一,其非线性系统响应特性是发射器特定属性的主要原因之一,也称为指纹信息。一般采用泰勒多项式信号模型表示每个发射器的独特非线性特征。对于发射器k,功率放大器的输出信号表示为:
(1)

sn=xnej2πnfT
(2)

图2展示了具有k个发射器的雷达辐射源个体识别系统,该系统根据不同的泰勒多项式系数提取雷达辐射源信号所携带的个体指纹信息来区分不同的个体。
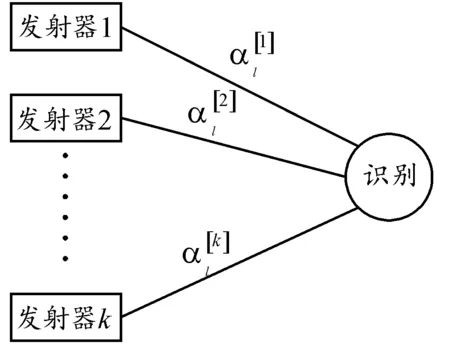
图2 雷达辐射源个体识别系统Fig.2 Radar emitter individual identification system
1.2 双谱估计
双谱是处理非平稳、非线性雷达辐射源信号的有力工具。设xm是一个真实的非平稳信号。基于高阶谱分析(higher-order spectral analysis,HOSA)理论,双谱分析是三阶累积量的二维傅里叶变换。在高阶谱中,双谱的阶数最低,计算量最少。本文中使用双谱估计间接法[24],计算步骤如下。
步骤1将原始数据集xm分为k段,每段含M个点。
步骤2设x(k)(0),x(k)(1),…,x(k)(M-1)为第k段数据,计算各段的三阶累积量的估计值:
(3)
式(3)中:k=1,…,K,M1=max{0,-i,-j};M2=min{M-1,M-1-i,M-1-j}。
步骤3取所有段的三阶累积量的平均值作为整个观测数据组的三阶累积量估计,即:
(4)
步骤4计算双谱估计:
(5)
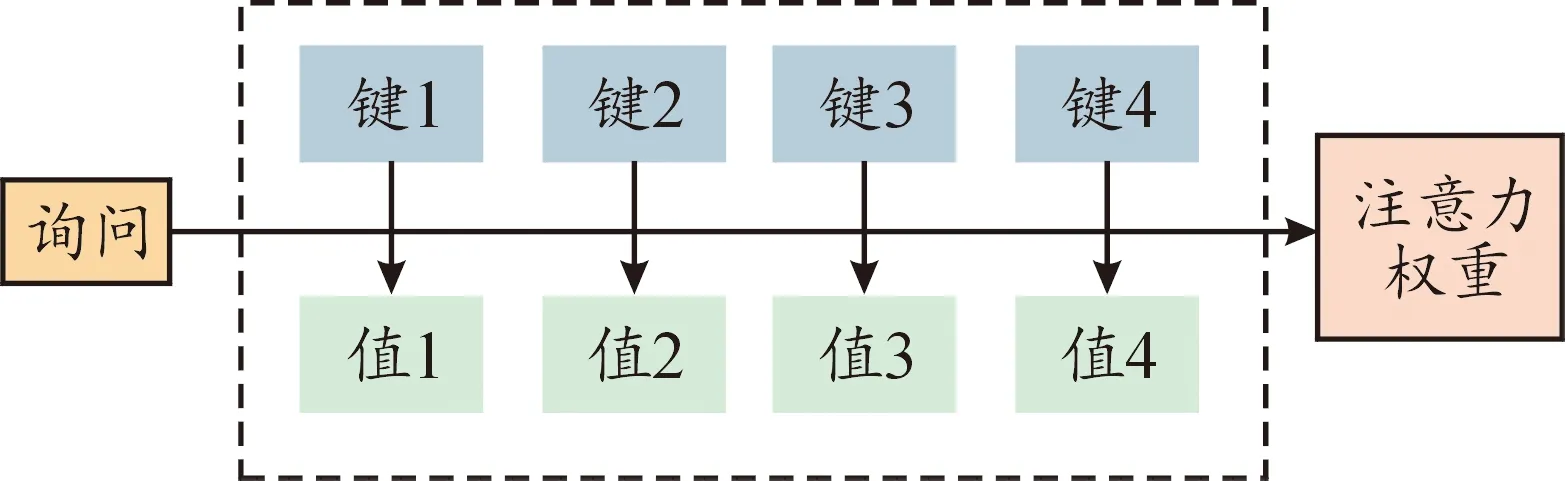
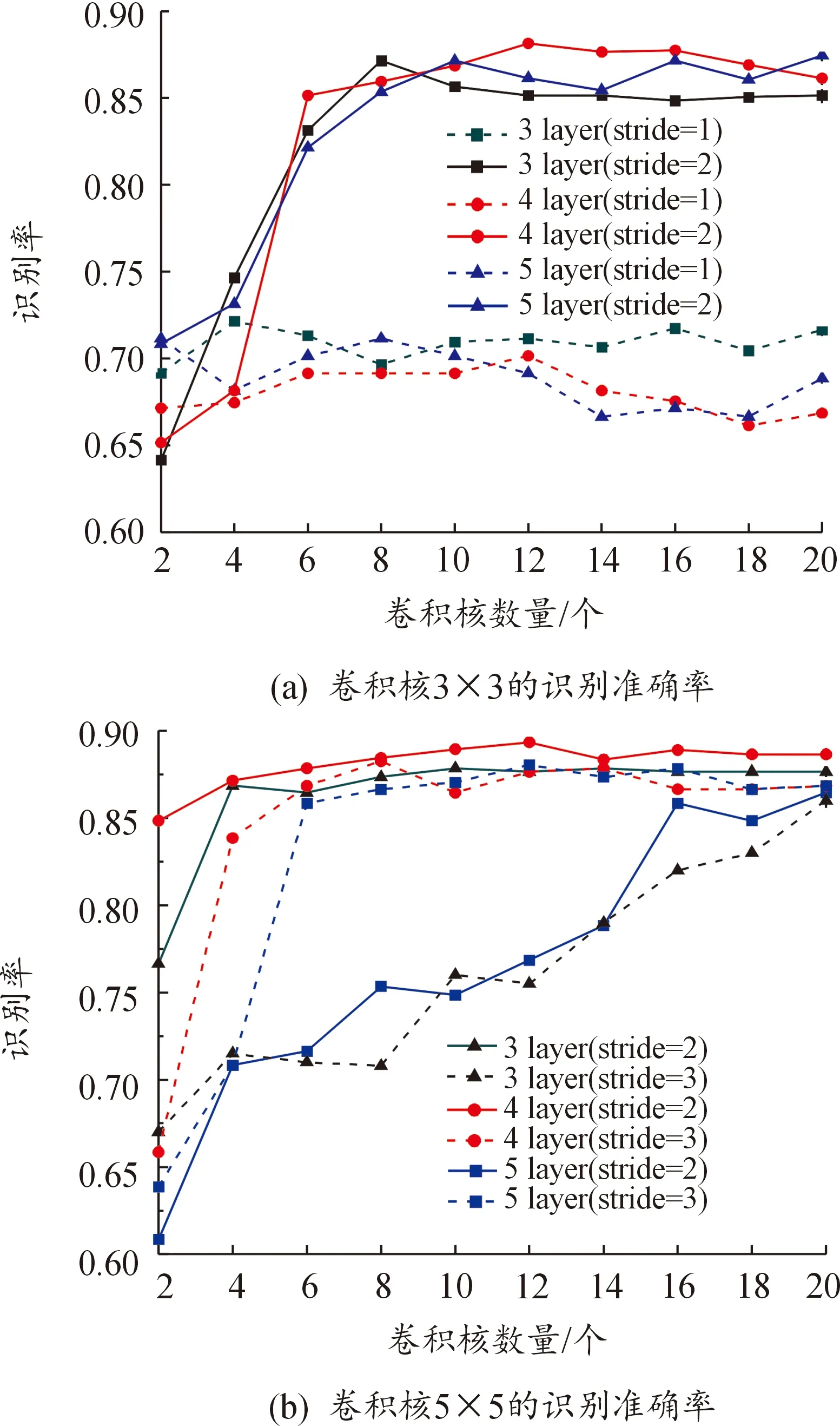
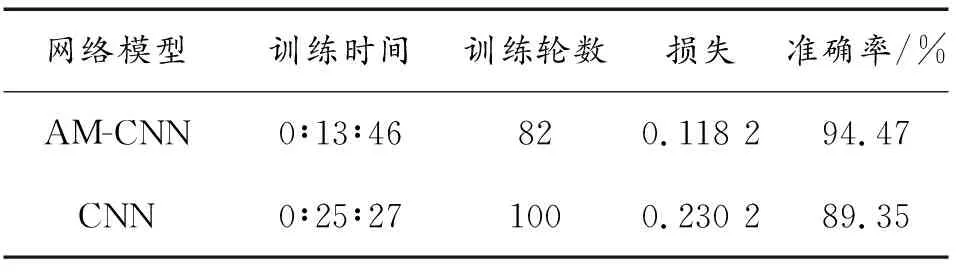
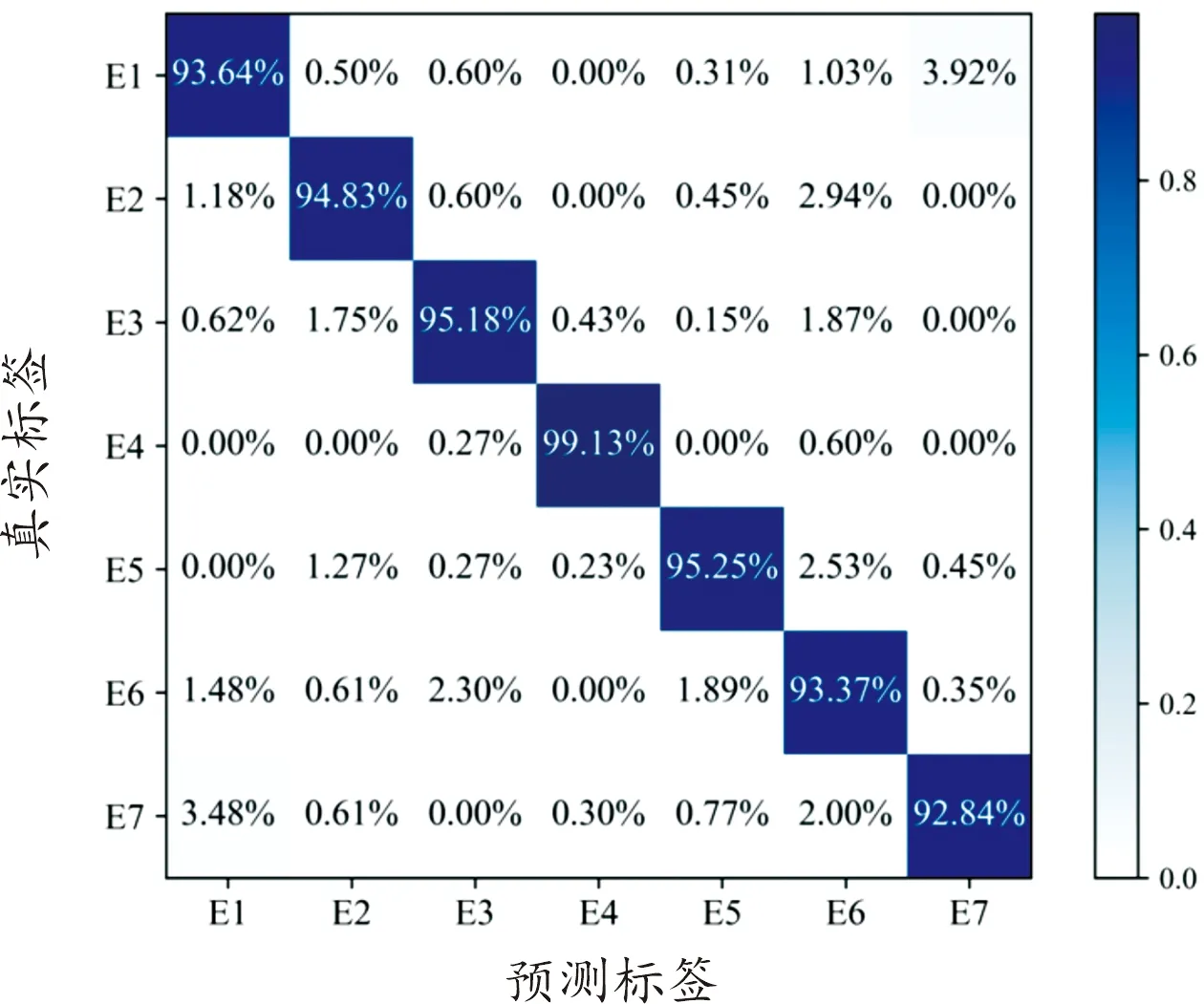
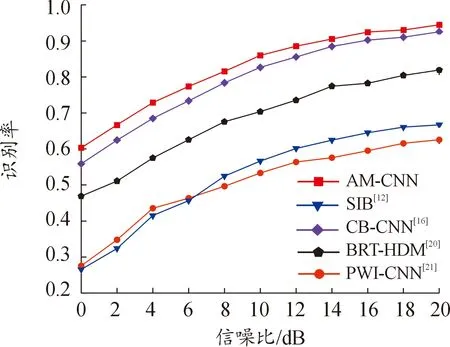
式(5)中:L 图3展示了一个使用Matlab HOSA工具箱双谱函数生成分辨率为256×256的雷达信号双谱图示例,它是一个雷达辐射源的双谱图。使用此类双谱图作为AM-CNN网络模型的输入。 图3 双谱图Fig.3 Bispectrum image 近年来,注意力机制不断应用在深度学习中的图像识别领域,从本质上讲,深度学习中注意力机制和人类选择性视觉的注意力机制相似,从当前所有信息中选择更关键的信息[26]。在深度学习网络模型中输入雷达辐射源个体的双谱图时,当图像数量越多,网络训练会出现过拟合现象,注意力机制可以有效解决这个问题。 注意力机制的本质思想就是将雷达信号双谱图中的元素构成一系列(“键”“值”)对,然后给定识别结果中某一元素的“询问”,通过计算此“询问”和不同“键”之间的相关性,得出每个“键”所对应“值”的权重系数,然后对其加权求和,最终得到注意力数值。从而实现输入信息与识别结果快速、高效地匹配。注意力机制原理如图4所示。 图4 注意力机制原理Fig.4 Principle of attention mechanism 注意力机制原理可以归纳为以下3步计算过程。 步骤1计算各元素权值的相似度得到权重,即: yi=X(Q,Ki) (6) 步骤2使用Softmax函数对步骤1结果归一化,并突出重要元素的权重,即: (7) 步骤3最后将上一步得到的关注元素权重与加权后各元素的权值进行加权求和得到注意力权重,即: (8) 雷达辐射源个体识别不同于传统的个体识别任务,它对识别精度和时间要求较高,为了提升CNN网络对雷达辐射源个体的识别准确率,减少识别时间,本文中从卷积层数、卷积核数量、卷积核大小、卷积核步长和引入自我注意力机制等5个方面对网络进行优化,以达到更好的识别效果。 卷积层数是影响深度学习模型性能的重要原因之一。通常情况下,卷积层越多,网络提取特征越明显,个体识别性能越好。但是,雷达信号数据特征的抽象水平较低,网络的层数没有必要过多,加之,深度网络具有复杂度高、训练效率低的特点,在一定程度上会影响模型参数更新的速度。因此,需要对卷积层数进行优化。 卷积核可以提取特定数据的特征,多个卷积核可以提取多种特征,从而提高识别精度。但是,雷达信号特征相对较少,卷积核数过多会导致网络冗余,影响到整个网络训练的结果。小卷积核的参数少,计算量小,但小卷积核无法完全提取雷达辐射源信号的双谱特征。卷积核通常以一定步长移动,为防止特征信息丢失,步长一般小于卷积核大小。较小的卷积核步长可以充分提取指纹特征,但会出现拟合现象,减少模型泛华能力。 将注意力机制模块引入现有的网络模型中,在保持原有网络模型的基础上,减少网络的识别时间,提高识别准确率。 AM-CNN网络采用简单有效的网络结构,包含4个二维卷积层、1个注意力机制层、1个全连接层。具体网络模型如图5所示。 图5 AM-CNN模型Fig.5 AM-CNN model 二维卷积层包括卷积层、批归一化(batch normalization,BN)层、激活函数层和池化层。在卷积层中,卷积核大小为5×5,卷积核数量为12,步长为2。在网络中引入BN层,可以加速网络的收敛速度,同时,允许使用较大的学习率,让网络训练变得更加容易。激活函数层使用LeakyReLU函数,目的增加非线性度。池化层选择最大池化层,大小为3,步长为1。在全连接层之前加入自我注意力机制模块。用注意力单元检测CNN输出特性,将更大限度地提高分类识别效果。最后通过Softmax层输出分类结果。损失函数采用categorical_crossentropy,优化器采用Adam,学习率初始设置为0.001,batch_size大小为64,训练轮数为100轮,设置EarlyStopping,防止在测试集上测试误差上升,避免继续训练导致过拟合问题。 具体算法流程如下: 步骤1将原始信号分解为k段,每段含M个点。 步骤5利用双谱特征图作为AM-CNN模型输入进行训练,得出最优的网络权值并保存模型。 步骤6同步骤1~步骤4计算测试集的双谱特征图。 步骤7利用训练好的AM-CNN模型识别测试集。 本文中所使用的数据集参照2.1节系统模型生成7个雷达辐射源个体,泰勒多项式的阶数为3,具体系数见表1[17],雷达辐射源信号的调制样式为线性频率调制,载波频率为20 MHz,采样频率为10 MHz,带宽为10 MHz,脉冲重复周期1 ms,脉冲宽度为200 μs。通过添加高斯白噪声改变信噪比,采用Matlab仿真生成实验数据,信噪比由0~20 dB间隔2 dB,共11种信噪比,各信噪比下不同雷达辐射源的样本数量为2 000个。对于7个辐射源使用标签E1,E2,…,E7。将数据集按7∶3的比例划分,1 400个样本用于训练数据,600个样本用于测试数据。 表1 不同雷达辐射源个体的泰勒多项式系数Table 1 Taylor polynomial coefficients of different radar emitters 实验采用的测试平台为Intel Core i9-9900,NVIDIA GTX2080Ti。本文中神经网络模型是在TensorFlow 2.4.0平台上搭建的,学习框架采用Keras 2.3.1,编译器为PyCharm2021.3.1 x64,编程语言为python 3.6。 图6展示了卷积层数、卷积核数量、卷积核大小、卷积核步长对识别率的影响。在图6(a)中,卷积核大小设置为3×3,步长分别设置为1和2,在图6(b)中,卷积核大小设置为5×5,步长分别设置为2和3,训练具有不同卷积层数和不同卷积核数的CNN网络,训练后的最优模型用于识别测试集。 图6 不同卷积核分析Fig.6 Different convolutional kernel analysis 根据图6可以得出以下结论: 1) 不同的参数对识别性能有显著影响。当卷积核步长为1时,模型重复计算数据中的噪声,使得泛化能力较差。因此,总体识别率较低,且随卷积核数的变化而波动。当卷积核步长为2时,可以在一定程度上避免噪声的影响,可以有效地提取信号指纹特征。 2) 当卷积核大小、步长和卷积层数固定时,识别率随着卷积核数增加而增加,提取信号指纹特征越充分,当增加到一定数量后,识别率趋于平稳,不会再继续提高。 3) 从实验结果可以得出,卷积层数为4,步长为2时,对卷积核数变化的鲁棒性最强,识别性能最好。当卷积层数和步长继续增加,会导致特征维数减少,提取特征不充分,从而影响识别率。 4) 当卷积层数为4,步长为2时,卷积核为5×5的网络识别性能优于卷积核为3×3的网络,其中,当卷积核大小为5×5,卷积核数为12时,其识别率最高,达到89.35%。 综上所述,卷积层数、卷积核数量、卷积核大小、卷积核步长对识别结果均有影响,通过实验结果得出最优的CNN参数:卷积核大小为5×5,卷积核的步长为2,卷积层的数量为4,卷积核的数量为12。 在优化后的CNN网络模型基础上,探究注意力机制是否能进一步提升CNN网络对雷达辐射源个体的识别速度和准确率,实验结果如表2所示。 表2 注意力机制对网络分类能力的影响Table 2 The effect of attention mechanism on network identification ability 由表2可知,在优化的CNN网络模型基础上,引入注意力机制的AM-CNN模型与原CNN模型相比,训练轮数减少18轮,损失函数较低0.12,训练时间减少一半,识别准确率提升5%。 为了检验AM-CNN算法对雷达辐射源个体的识别能力,本小节采用混淆矩阵对7个模拟雷达辐射源个体的识别准确率进行具体分析。 由图7可知,对7个模拟雷达辐射源个体进行实验,辐射源E4的识别效果最好,辐射源E1和E7的错分概率较高,这是由于泰勒多项式系数的差异对辐射源个体识别的影响。可以得出,不同阶数的系数对辐射源个体的影响是不同的,阶数越高对识别效果影响越小,反之,阶数越低,影响越大。整体来说,识别准确率在92.84%~99.13%,达到较好的识别水平。 图7 混淆矩阵Fig.7 Confusion matrix 为了进一步验证该方法的有效性,将AM-CNN方法与现有4种方法进行比较,包括文献[12]中SIB方法、文献[16]中CB-CNN方法、文献[20]中BRT-HDM方法和文献[21]中PWI-CNN方法。具体实验结果如图8所示。 图8 5种方法的不同信噪比识别准确率图Fig.8 Identification accuracy of five methods with different signal to noise ratio 由图8可知,就识别率而言,随着信噪比增大,AM-CNN算法的识别性能随之提高,相较于其他4种算法,AM-CNN算法有较好的表现。在6 dB以上时,识别率超过80%,在20 dB,识别率达到了94.47%。结果表明,AM-CNN算法可以利用雷达发射机输出的稳态信号识别辐射源个体,这主要是AM-CNN模型有效地提取了雷达辐射源信号的双谱特征,更好地抑制了高斯噪声,并且具备强大的自学习能力以及对雷达辐射源信号指纹特征地充分提取,因此具有较高的识别率,但在实测数据集的性能方面需要进一步提高。 在CNN的基础上,结合注意力机制,通过调节卷积核的大小、步长、数量和卷积层的数量等参数优化网络模型。实验结果证明,本文中提出的AM-CNN算法相较于CNN算法,识别准确率提高了5%,训练时间缩短一半。在不同信噪比条件下能够有效识别7种雷达辐射源个体,与现有方法对比,AM-CNN算法具有抗噪性能好、识别准确率高的特点,有效提升了对雷达辐射源个体的识别能力。
1.3 注意力机制
2 AM-CNN模型
2.1 CNN模型优化
2.2 AM-CNN模型及参数设置

2.3 算法流程

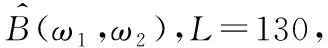
3 实验与结果分析
3.1 实验数据

3.2 实验对比与分析
3.3 性能评估
3.4 对比分析
4 结论

