基于刚度匹配的电磁轨道发射器减振优化

任师达,冯 刚,刘少伟,胡 静,李腾达

(1.空军工程大学 防空反导学院, 西安 710051; 2.火箭军工程大学 基础部, 西安 710025)

0 引言

电磁发射技术是一种运用电磁力将弹体加速至超高声速的新兴武器发射技术[1-4]。该技术能够突破传统火药发射的速度极限,并通过控制激励脉冲电流实现对出膛速度的精确控制。在电磁轨道发射器发射过程中,电枢的超高速滑动将导致电磁轨道发射装置产生剧烈振动,严重影响发射器的发射效能和使用寿命[5-8]。因此在实际工程应用中,通常采用弹性支撑装置对电磁轨道发射器进行紧固,以达到减振的目的[9-11]。

针对电磁轨道发射装置的振动与减振优化问题,国内外学者开展了大量研究。Tzeng等认为电磁轨道发射器的动态响应是由电枢移动磁压力所导致的,其推导了动态载荷下发射器的振动控制方程,分析了不同材料、几何形状以及轨道截面下的临界速度[12];Daneshjoo K等建立了动态载荷下电磁轨道发射器轨道的振动控制方程,根据各项参数求得临界速度和外载荷作用下的轨道变形[13];Nechitailo N V等开发了2种解析算法求解电磁轨道发射器的临界速度和动态变形量[14];田振国等提出采用合理复合层占比的复合轨道能够改善轨道的动态响应[15]。这些研究大都采用均布载荷和电枢匀速运动来求解,简化后的动力学模型存在着一定的误差,以及对于电磁轨道发射器具体的减振优化结构的研究也比较少。

本文基于支撑结构刚度匹配对电磁轨道发射器进行了减振优化,建立了轨道-弹性支撑结构模型,分析了绝缘体结构的力学特性,探讨了轨道-弹性支撑结构的刚度匹配关系。提出2种减振结构:针对双层复合绝缘体的结构设计,基于响应面法进行了刚度匹配实验,建立了响应面模型,分析了变量灵敏度并根据条件约束进行了结构刚度匹配选择;针对轴向多刚度弹性支撑的结构设计,建立了轴向多刚度弹性支撑模型,仿真分析了轴向多刚度弹性支撑的减振性能。

1 轨道-弹性支撑结构模型

1.1 模型的建立

电磁轨道发射器基本结构示意图如图1所示,其中由外围封装、绝缘体以及螺栓预紧件共同组成的弹性支撑用于抵抗轨道变形,保持枢轨之间的有效滑动电接触。同时弹性支撑在轨道发射过程中还需要面对瞬时变化的发射工况,尤其是在临界速度条件下,对轨道振动有着重要影响,对其结构进行优化设计,有利于缓解轨道振动。

图1 电磁轨道发射器结构Fig.1 Cross section diagram of electromagnetic rail launcher

在建立的发射器结构基本有限元模型中,发射器的口径为20 mm×35 mm,轨道的几何参数为1 000 mm×30 mm×10 mm,螺栓预紧力为1.2 MN,电枢与轨道的材料参数如表1所示。其中,弹性支撑材料选择环氧树脂(玻璃钢),其弹性模量为各向异性,分别为45、10、10 GPa。

表1 电枢与轨道材料参数Table 1 Material parameters of armature and rails

1.2 绝缘体结构的力学特性分析

电磁轨道发射器静荷载下绝缘体的受力情况如图2、图3所示。由图2、图3分析可知,在电磁轨道发射器静荷载下,绝缘体主要受到外围封装上的螺栓预紧件施加的压应力以及电枢过盈导致轨道变形的挤压应力。在绝缘体外表面,支撑结构尖角处存在规律性的应力集中现象,其与外围封装的预紧件分布位置及大小有关;在绝缘体内表面,电枢加载对应位置有明显的应力集中,其与电枢过盈量以及轨道材料刚度有关。

图2 静荷载下绝缘体外表面受力Fig.2 Stress on external surface of insulation under static load

图3 静荷载下绝缘体内表面受力Fig.3 Internal surface stress of insulation under static load

图4、图5分别为电磁轨道发射器在临界速度时刻绝缘体的受力情况。

图4 临界速度时刻绝缘体外表面受力Fig.4 Stress on external surface of insulation at critical speed

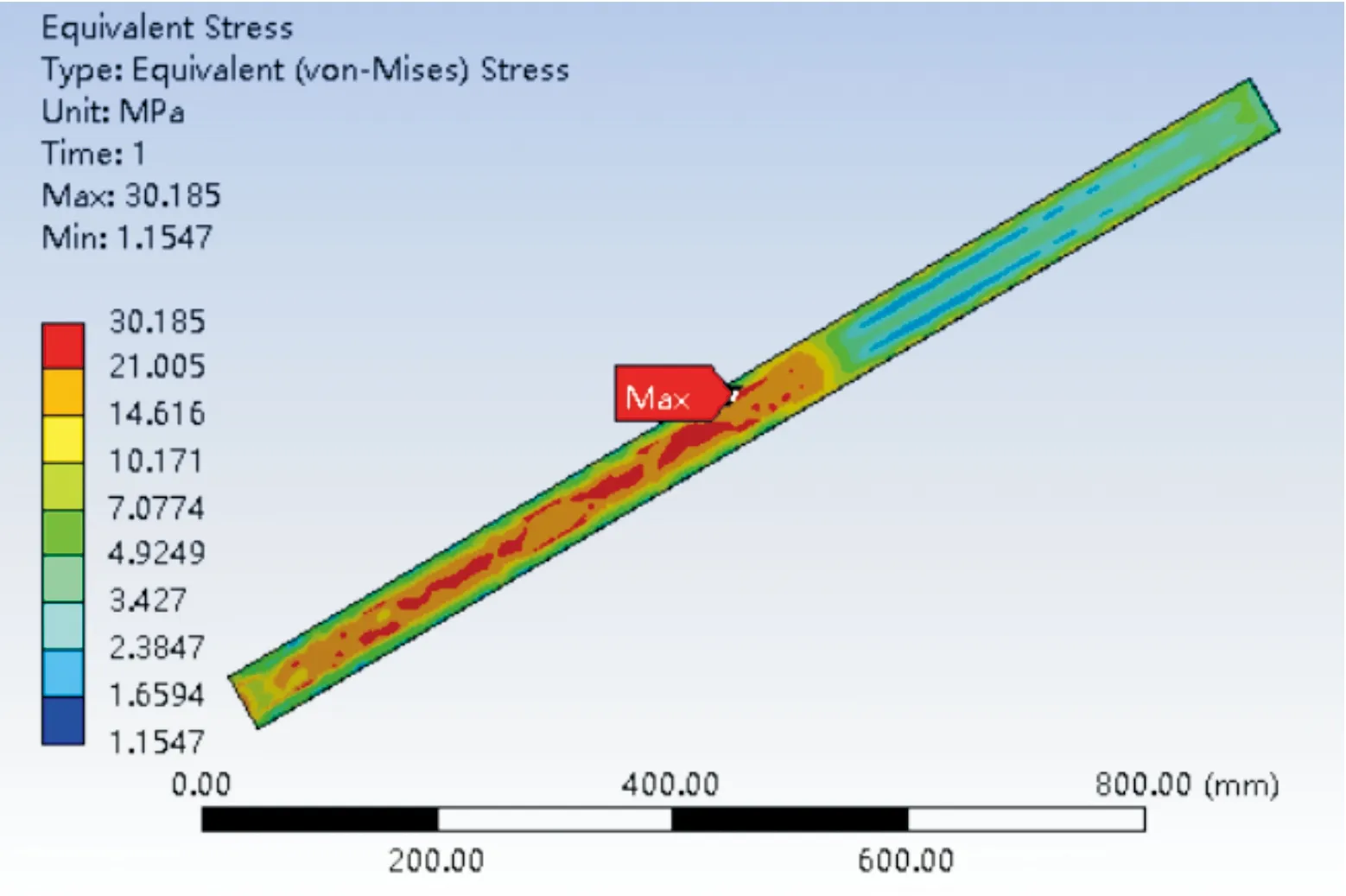
图5 临界速度时刻绝缘体内表面受力Fig.5 Stress on inner surface of insulation at critical speed

由图4、图5分析可知,在电磁轨道发射器发射过程中,绝缘体除了受到外围封装上的螺栓预紧件施加的压应力以外,还受到电枢过盈、轨道所受电磁排斥力以及轨道振动等因素导致轨道变形的挤压应力。可以看出,临界速度时刻,绝缘体主要是在轨道通流部分对应位置处受到轨道电磁排斥力的挤压作用,并且在电枢所处对应位置达到应力集中最大值,为30.185 MPa。

1.3 轨道-弹性支撑的刚度匹配关系

在电磁轨道发射器的振动中,轨道与弹性支撑作为主体结构,其在轨道-支撑结构切向受力最为显著,因此在设计过程中,主要考虑轨道与弹性支撑结构的材料在切向上的刚度匹配关系。

定义轨道与弹性支撑结构的刚度匹配关系为

(1)

在对弹性支撑结构的减振优化过程中,引入了轨道与弹性支撑结构的刚度匹配系数,从而控制整个发射器的刚度匹配关系。在刚度匹配设计中,目标函数为轨道的临界速度更大,振动响应最小,且使优化得到的发射器结构满足刚度要求、强度要求、变形约束。

其具体定义如下:

1) 刚度要求。按照轨道材料、弹性支撑材料的可用刚度作为约束边界,并研究不同刚度比下的轨道-弹性支撑结构对减振优化效果的影响。

2) 强度要求。要求在大载荷作用下发射器结构不发生材料失效,以工程上常用的最大许用应变准则来判定是否失效,同时要求发射器结构均能够满足拉、压、剪切的设计许用值。

3) 变形约束。要求在大载荷作用下,依然满足枢轨的良好电接触,保证接触压力满足“1A/g”准则[16]。

2 双层复合绝缘体结构设计

为了同时较好地满足发射器的横向稳定性和垂向弹性,双层复合绝缘体结构采用内外两层不同力学特性的材料,其提供的横向和垂向刚度能够较好地满足发射器结构在各个方向上的力学性能要求。

双层复合绝缘体结构的刚度受到内外两层材料的弹性模量影响,需要分析各层材料的弹性模量和刚度之间的匹配关系,通过选择合理的材料弹性模量以达到较好的刚度匹配关系,从而起到减振的最终目的。

2.1 双层复合绝缘体结构模型

图6为双层复合绝缘体结构示意图,即将原绝缘体结构划分为两层,为便于仿真分析,设定每层的尺寸相同,只对两层绝缘体材料的刚度匹配关系进行分析。

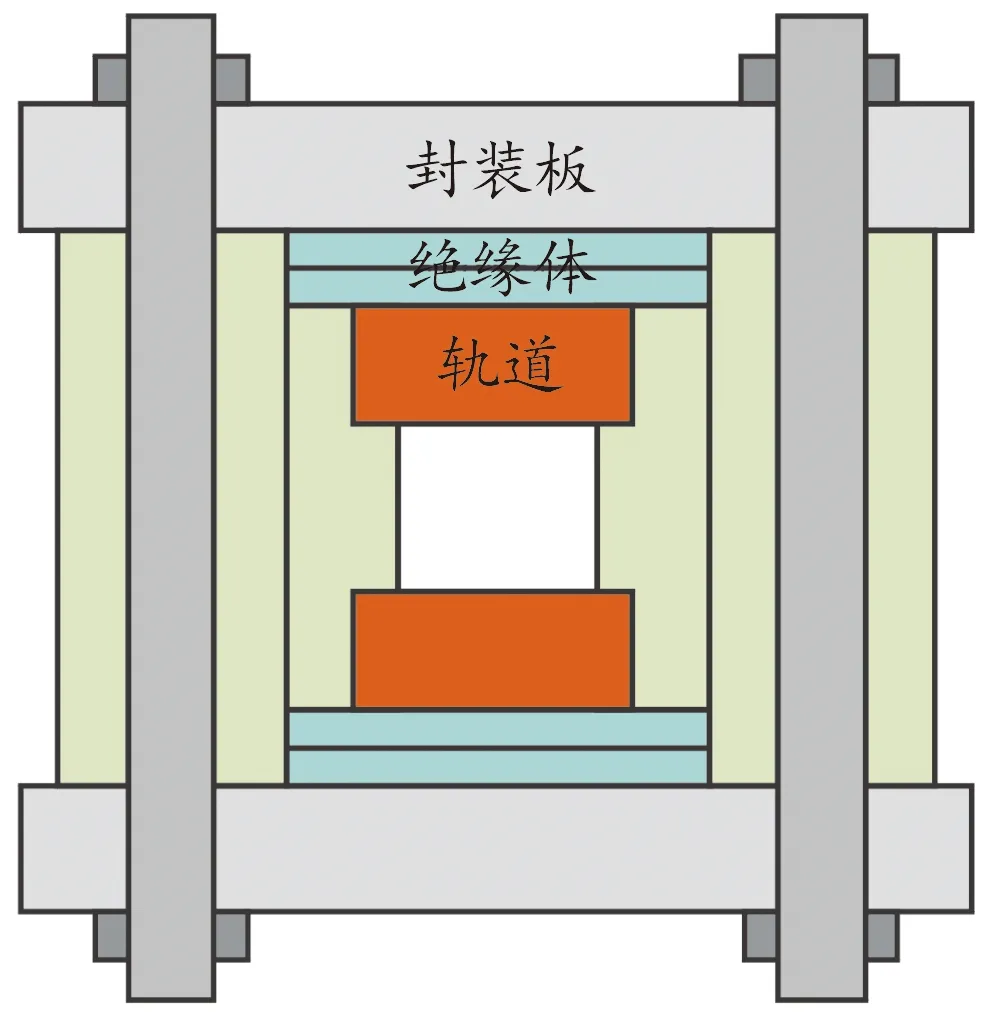
图6 双层复合绝缘体结构示意图Fig.6 Structural diagram of double-layer composite insulator

2.2 基于响应面法的刚度匹配试验

双层复合绝缘体结构应具备合适的刚度以控制轨道在不同方向上的垂向位移与挠曲变形,但是若刚度过大也会导致轨道振动过程中应力集中及磨损加剧,这无疑会影响轨道的使用寿命。绝缘体结构材料的力学性质是影响轨道刚度的重要因素,本节通过分析绝缘体结构材料的弹性模量与轨道整体刚度之间的联系,建立拟合曲面来确定最佳的弹性模量组合以匹配预计的轨道刚度。

在发射器有限元模型中,双层复合绝缘体结构之间采用实体粘结处理,具备良好的整体性。在电磁轨道发射器发射过程中临界速度时刻轨道产生共振,此时轨道上的变形与应力集中现象最为严重,对发射器轨道的强度要求很高,这就要求绝缘体紧固提供一定的限制支撑作用,起到减振的目的。对于双层复合绝缘体结构的刚度匹配分析需要在临界速度时刻进行,满足该时刻的刚度强度要求的刚度匹配关系能够起到较好的减振作用。

响应面法(response surface methodology)是一种统计学方法,通过设计综合实验来对一个复杂系统的输入与输出之间的函数关系进行分析。其在实验数据的基础上,将预计目标的实验数据进行拟合,得到变量与响应之间的函数关系,最终可通过变量与响应之间的拟合函数关系构造出响应曲面,得到预计目标响应值所对应的变量组合水平[17]。

响应面法具有多种不同的实验方法,但针对双层复合绝缘体结构而言,变量取2种紧固材料的弹性模量,变量较少。BBD(box behnken design)试验方案的试验次数较少且能够保证求解出的变量组合水平在许可范围内,比较适合于双层复合绝缘体结构的刚度匹配优化,因此采用BBD试验方案进行设计优化。

通过试验将内外两层绝缘体材料的弹性模量作为离散变量,即在试验过程中使内外两层材料的弹性模量同时变化。内外两层绝缘体材料的弹性模量取值如表2所示(其中En为内层绝缘体材料弹性模量,Ew为外层绝缘体材料弹性模量),共9种变量组合。

表2 内外两层绝缘体材料的弹性模量取值Table 2 Values of elastic modulus of inner and outer insulator materials

将各变量组合对应的材料参数输入有限元模型,可以计算出对应的临界速度时刻轨道的最大垂向位移dc和最大剪切应力τh。表3为各变量组合对应的试验结果。

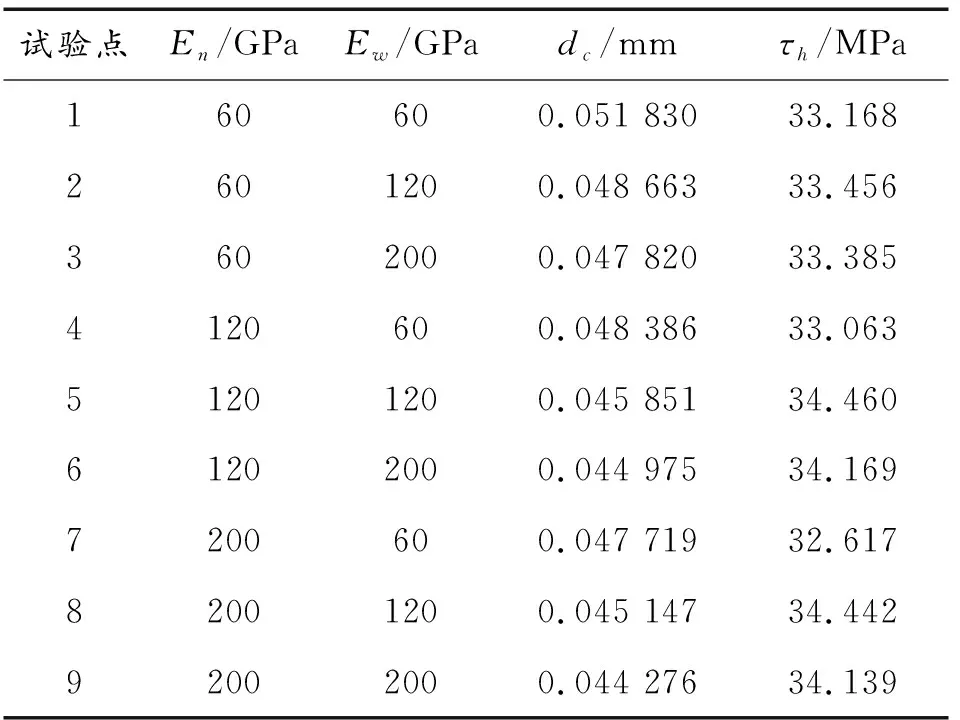
表3 各变量组合对应的试验结果Table 3 Test results corresponding to each variable combination

2.3 响应面模型建立与求解

为了建立电磁轨道发射器的振动特性与双层复合绝缘体结构材料的弹性模量之间的关系,根据表3中的试验点所对应的临界速度时刻轨道的垂向位移和最大剪切应力的响应值,并按照试验点的试验变量与响应值之间的关系建立双层复合绝缘体结构刚度匹配的二次多项式响应面模型。

响应面模型可以表示为

(2)

其中:Ym(X)(m=1,2)为临界速度时刻轨道的垂向位移dc和最大剪切应力τh;X=(A,B)T为设计变量的列向量;xi和xj(i,j=1,2)为设计变量的各分量;a0,ai,aii和aij为待定系数,aii为xi的二次效应,aij为xi和xj之间的交互作用效应。

式(2)可改写为

Ym(X)=DmBm+εm

(3)

其中:Dm为有9组试验点组成的设计变量矩阵;Bm为响应面模型中的未知系数矩阵,εm为误差项矩阵。

采用最小二乘法对响应面模型进行求解,即

(4)

由式(4)可得双层复合绝缘体结构刚度匹配的响应面模型,临界速度时刻轨道的垂向位移dc和最大剪切应力τh的响应面模型具体表达式分别为:

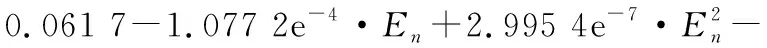
2.561 4e-8·EnEw

(5)

6.041 3e-5·EnEw

(6)

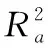
(7)

(8)

(9)

(10)

fz=M-1

(11)

(12)

fc=M-N

(13)

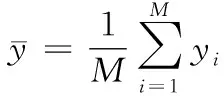
(14)

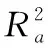
表4 响应面模型的误差分析Table 4 Error analysis of response surface model

2.4 变量灵敏度分析

为了研究内外层绝缘体结构的弹性模量对响应的影响,假设当设计变量由S1变化为S2时,轨道的振动响应由M1变为M2,则该设计变量的灵敏度定义为

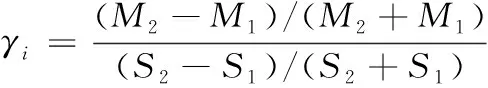
(15)

其中,γi(i=1,2)分别为设计变量对临界速度时刻轨道的垂向位移dc和最大剪切应力τh的灵敏度。

当对某一设计变量进行计算的时候,另一变量应取初始值,则令内外两层绝缘体材料的弹性模量的初始值均为60 GPa,计算结果如表5所示。

由表5可知,内层绝缘体材料的弹性模量对临界速度时刻轨道的垂向位移dc和最大剪切应力τh外的影响较外层绝缘体材料的弹性模量更大。对于轨道变形,增大内外层绝缘体材料的弹性模量均能够减小临界速度时刻轨道的垂向位移。对于轨道所受应力,内层绝缘体材料的弹性模量对最大剪切应力的灵敏度为负,外层绝缘体材料的弹性模量对最大剪切应力的灵敏度为正,即内层绝缘体材料的弹性模量越大,临界速度时刻轨道的最大剪切应力越小,而外层绝缘体材料的弹性模量越大,临界速度时刻轨道的最大剪切应力反而越大。内外层绝缘体材料的弹性模量对2个响应值的影响规律,应结合响应曲面,具体分析。

表5 设计变量对响应值的灵敏度Table 5 Sensitivity of design variables to response values

2.5 结构刚度匹配选择

2个响应值与设计变量的拟合曲面和等高线图如图7、图8所示。

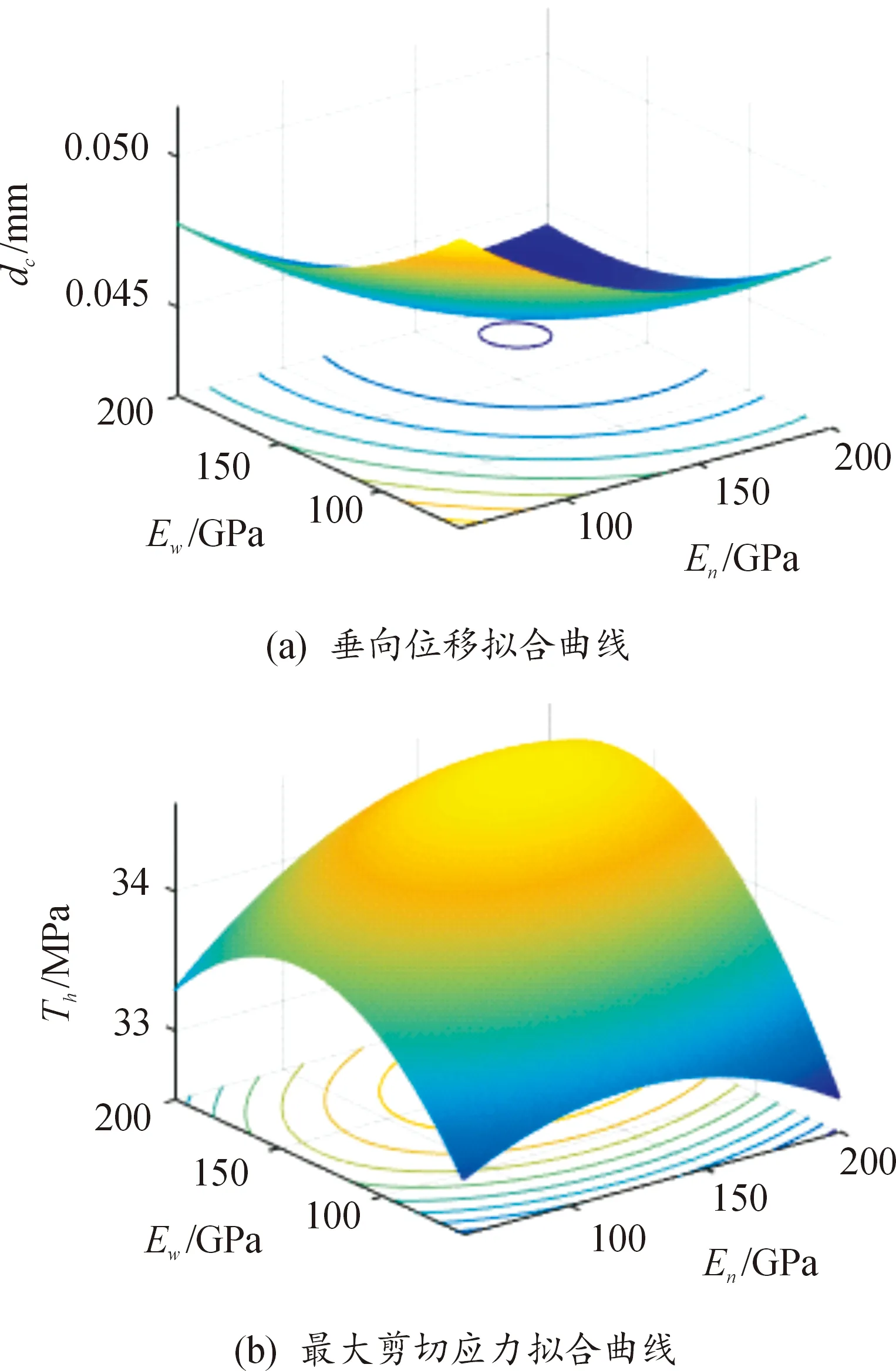
图7 2个响应值与设计变量的拟合曲面Fig.7 Fitting surface between two response values and design variables

结合变量灵敏度分析和拟合曲面变化趋势可知,临界速度时刻轨道的垂向位移dc与内外层绝缘体材料的弹性模量呈负相关,最大剪切应力τh与内外层绝缘体材料的弹性模量之间的关系变化较为复杂,其受外层绝缘体材料的弹性模量的影响较小。将等高线进行叠加之后,得到同时满足较小轨道垂向位移和较小最大剪切应力的取值区域,如图8中的阴影部分所示。En取值范围约为[90 GPa,200 GPa],Ew取值范围约为[0,80 GPa]。因此,在支撑结构的刚度匹配选择中,内外层绝缘体材料在弹性模量范围内取值时,双层复合绝缘体结构相比于原绝缘体结构具有更好地缓解轨道振动损伤的功效。

图8 等高线叠加图Fig.8 Contour overlay

3 轴向多刚度弹性支撑结构设计

3.1 弹性支撑结构的轴向多刚度分析

文献[9]中李腾达等提出的基于身管紧固的减振优化方法,发现身管紧固的方式会导致在紧固位置出现应力集中的负效应。轨道应力随着紧固的位置分布有较明显的波动,对轨道的强度有较高的要求,这无疑将对电磁轨道发射器的发射稳定性造成不良的影响。由此引申出整体、连续的预紧方案设想,但在工程中较难实现。

基于以上分析与设想,在弹性支撑结构的优化设计中,认为在轴向上由弹性支撑结构对轨道振动响应剧烈的位置提供更强刚度的支撑从而起到减振效果,是一种可行的方案。

对于不同电枢速度段的导轨,其对应位置的弹性支撑刚度的要求也不相同,初步将弹性支撑结构分为不同刚度的3段。其中高刚度段需同时覆盖共振和大变形范围。应用ANSYS软件对其结构进行模态叠加分析,得到轨道上下表面线变形云图如图9所示。

图9 轨道上下表面中线变形云图Fig.9 Cloud diagram of the deformation of the center line of the upper and lower surfaces of the rail

很明显,轨道大变形区域主要集中在de段(d点距起始段270 mm,e点距离起始段670 mm),据动力学仿真可知,电枢通过此段导轨的速度范围为1 093～1 557 m/s,跨越了临界速度1 448 m/s。因此de段满足高刚度段需求。

3.2 轴向多刚度弹性支撑结构模型

依据上述分析,建立轴向多刚度弹性支撑结构模型如图10所示。

图10 轴向多刚度弹性支撑结构示意图Fig.10 Schematic diagram of axial multistiffness elastic support structure

在距轨道起始端270 mm处400 mm长的区域采用较高刚度的弹性支撑材料,支撑2的刚度是支撑1、支撑3的2倍。

3.3 仿真结果分析

图11是单刚度下后半轨道多个位置挠度变化。图12是多刚度下后半轨道多个位置挠度变化。图13是单刚度下后半轨道多个位置振动加速度变化。图14是多刚度下后半轨道多个位置振动加速度变化。图15是2种结构下轨道各位置的最大剪切应力对比。

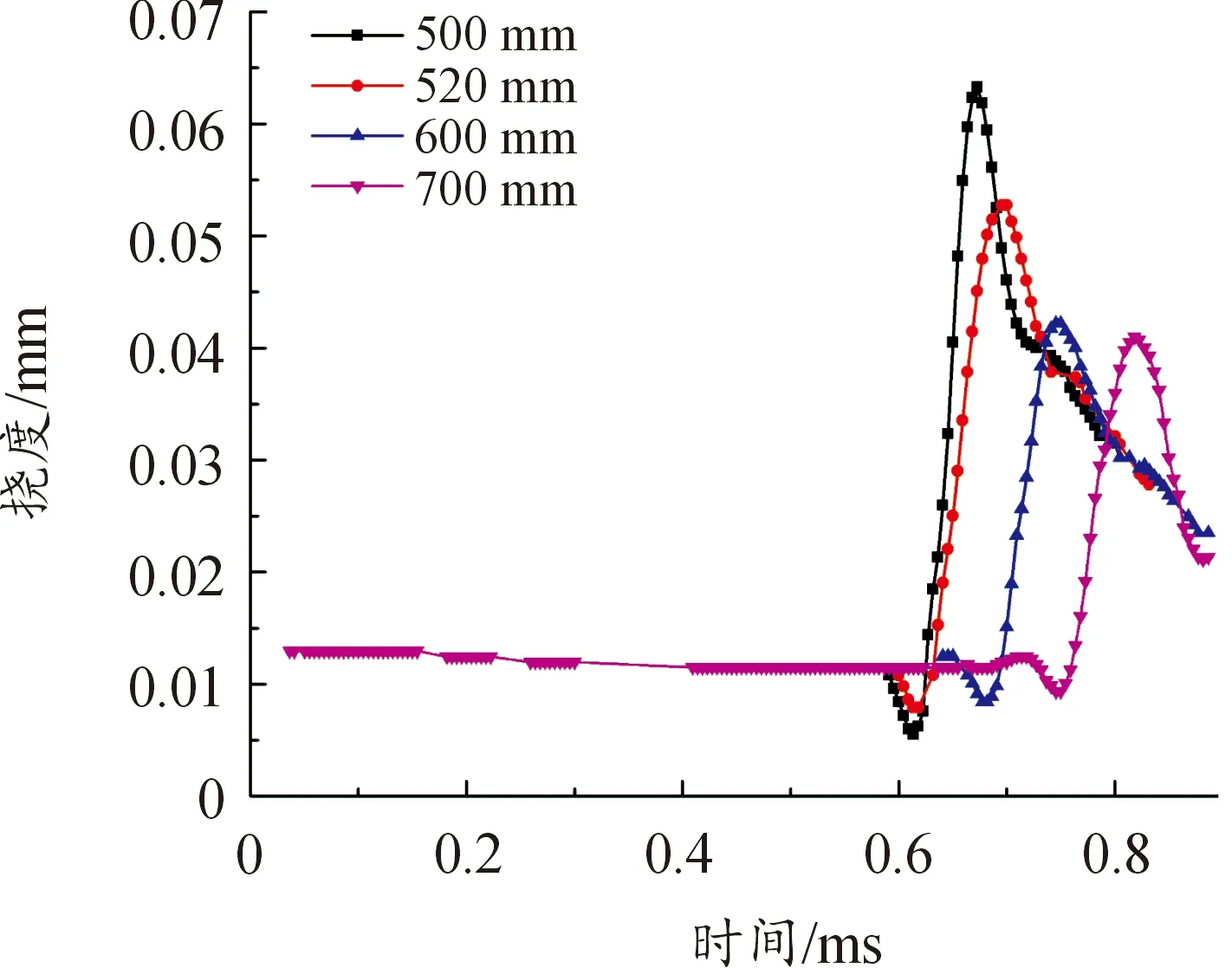
图11 单刚度下后半轨道多个位置挠度变化Fig.11 Deflection changes at multiple positions of the rear half rail under single stiffness

图12 多刚度下后半轨道多个位置挠度变化Fig.12 Deflection changes at multiple positions of the rear half track under multi stiffness

图13 单刚度下后半轨道多个位置振动加速度变化Fig.13 Variation of vibration acceleration at multiple positions of rear half rail under single stiffness

图14 多刚度下后半轨道多个位置振动加速度变化Fig.14 Variation of vibration acceleration at multiple positions of rear half rail under multi stiffness

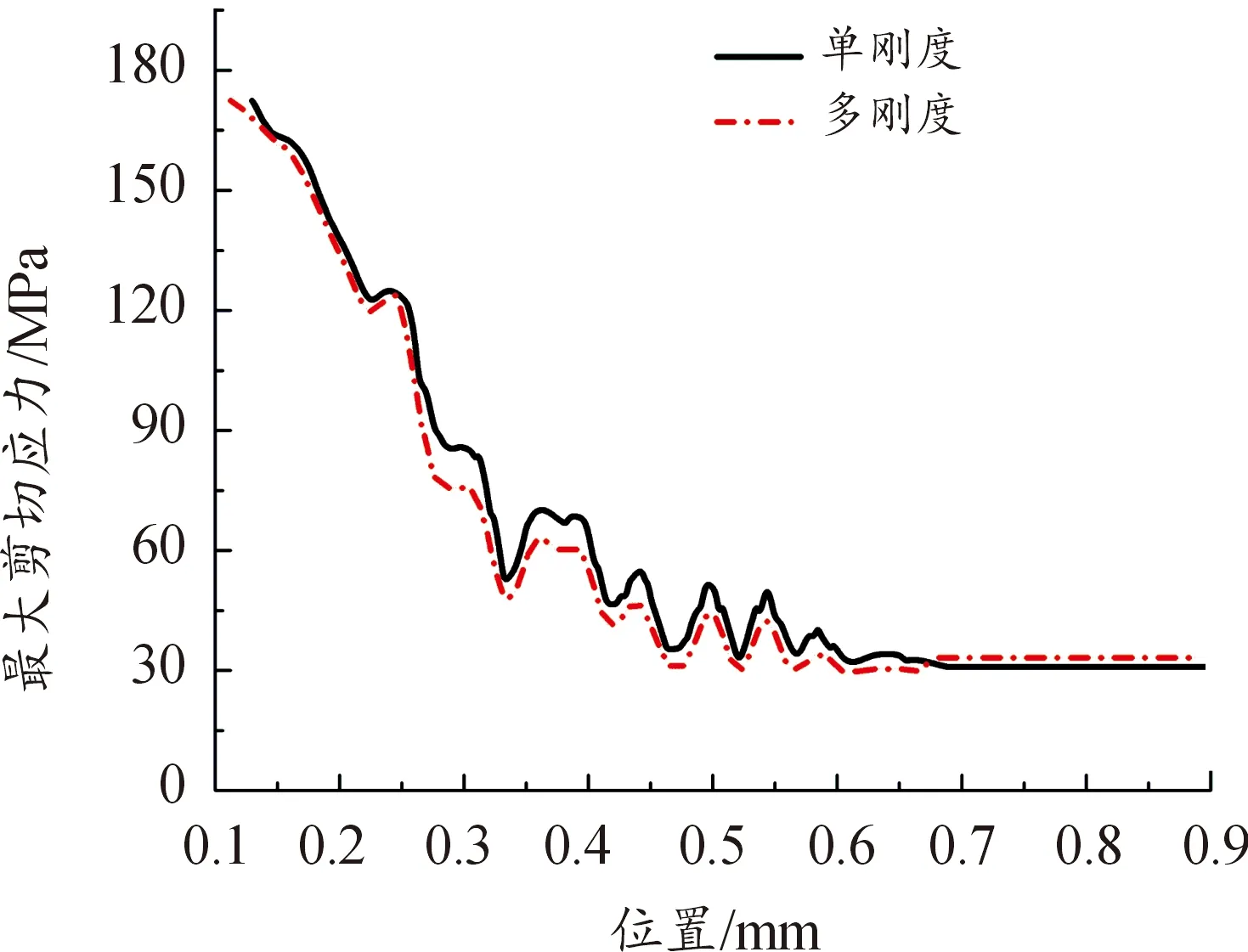
图15 2种结构下轨道各位置的最大剪切应力Fig.15 Maximum shear stress at each position of rail under different stiffness structure

由图11—图14可得,电枢在经过高刚度段时,该段轨道的挠度和振动加速度均较单刚度结构要小,其中4个位置处的峰值均有明显的降低。其中,轴向多刚度弹性支撑结构在高刚度段(500 mm处)的挠度峰值由单刚度时的0.0621 mm降低到了0.050 6 mm;轴向多刚度弹性支撑结构在高刚度段(500 mm处)的振动加速度峰值由单刚度时的9.3×10-5mm/s2降低到了7.3×10-5mm/s2。而当电枢通过高刚度段后,电枢前方的轨道振动挠度有所回升,振动加速度也开始有所波动,但仍未达到单刚度结构时的幅值,可见轨道振动放大的时刻得到了相应的延后。因此,采用轴向多刚度弹性支撑结构能够增强轨道刚度,有效地提高轨道的临界速度,使轨道发生明显振动波动的时刻延后,从而达到保持发射稳定性和延长发射器使用寿命的目的。

由图15可得,轴向多刚度弹性支撑结构下的刚度增强段所对应的最大剪切应力相较于单刚度结构有着明显地减小。可见,通过局部增强弹性支撑结构能够减小轨道的挠度变形,降低轨道所受的剪切应力,从而缓解轨道受到电枢的局部冲击,以及对轨道材料的强度要求。

通过对轴向多刚度弹性支撑结构下轨道的振动响应进行仿真分析,增强原临界速度段对应的弹性支撑刚度,能够有效地提高轨道的振动临界速度,从而减少轨道发生振动的时间,增强发射稳定性,延长轨道的使用寿命。

4 结论

通过对电磁轨道发射器振动特性和减振方法的研究,得到了发射过程中轨道的动力学响应规律,设计了2种具有工程应用价值的减振优化结构,能有效缓解轨道的振动损伤。主要结论如下:

1) 在对弹性支撑结构的减振优化过程中,通过引入轨道与弹性支撑结构的刚度匹配系数控制发射器刚度匹配关系,从而起到减振的最终目的。

2) 在双层绝缘体减振设计方案中,根据刚度匹配选择规律,当内层绝缘体材料弹性模量En为[90 GPa,200 GPa];外层绝缘体材料弹性模量Ew为[0,80 GPa]时,该方案相比于单层绝缘体结构具有更好的减振功效。

3)在轴向多刚度的减振设计方案中,采用三段不同刚度的弹性支撑结构能够有效提高了轨道的临界速度,减少振动时间,以达到延长发射器使用寿命的目的。