三维变分数值气象预报在弹道解算中应用研究

景银华,李 岩,陈 霖

(南京理工大学 能源与动力工程学院, 南京 210094)

0 引言

俄乌战争表明火炮仍是现代战争的主战武器,其低成本、快速响应和远距离精准打击能力是现代战场的迫切需求。在远程打击中气象是影响火炮射击精度的主要因素,在战时如何短时间内获取准确的气象数据已成为当前远程火炮快速射击的重点研究内容之一。数值气象预报提供网格化气象数据[1],能够涵盖全弹道段,可以实时预测射击时刻的气象数据,受环境限制小,这些优点使得其已然成为军事气象监测和保障的重要途径。

目前数值天气预报仍存在精度不足的问题,其应用于弹道解算中同探空气球获取的气象数据仍有一定差距,其重要误差来源之一是初始场误差[2-3],目前主流的减小初始场误差的方法是利用初始时刻的气象观测资料和背景场信息运用特定的资料同化方案进行改善[4]。WAHL D T[5]在改进有控弹药无人驾驶仪的过程中,在弹道解算环节引入数值天气预报,发现此方法可能够提升海军火炮的作战效能。张朝林等[6]对各种资料利用三维变分算法进行同化效果评估,指出对改进预报结果影响最大的为常规探空资料,地面常规观测资料作用次之。张利红等[7]对来源不同的探空观测资料基于三维变分算法进行同化分析,得出同化的探空资料数量越多,背景场改善效果越明显。资料同化能够进一步改善初始场,减小气象预报结果误差,这也使得数值天气预报在保障弹道解算速度的同时,能进一步提高弹道解算轨迹和落点的准确度。

本文中使用三维变分同化NCEP ADP全球高空观测天气数据,结合GFS再分析资料通过WRF进行气象预报,并将应用于有风状态下的6自由度弹道解算中,提出一种基于数值对比和弹道落点分析的方法,对资料同化在弹道解算用数值天气预报中的改善效果进行分析。

1 模型构建

本文中参考文献[8]构建了6自由度刚体弹道模型,此弹道模型在有风条件下的弹道方程为:

(1)

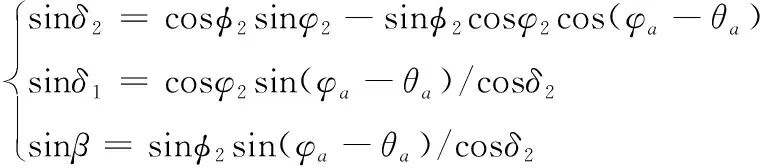
(2)

式(1)、式(2)中,各符号意义同文献[8]。

从方程推导及计算过程中可以看出,在远程打击中,随着弹丸飞行时间的增长,气象因素对弹丸飞行状态的影响也逐渐增大,本文中主要考虑气压、气温、湿度、风速及风向等气象要素。气压直接影响空气密度,随高度增大气压变低,弹丸所受空气阻力减小,射程增大。气温一方面通过改变空气密度进而影响气动力和气动力矩的计算来影响弹道,另一方面通过改变声速和阻力系数影响弹道,并且在阻力系数曲线的上升段和下降段,其影响不同[9]。湿度,一方面通过改变发射药和火炮等的性能而影响射击精度,另一方面通过影响各弹道高的空气密度大小,从而影响弹丸的飞行状态。风速和风向可以通过矢量分解为横风和纵风,进而影响弹道的计算。其中纵风会使火炮在水平射程上产生偏差,横风会使火炮产生侧向偏差。

数值天气预报(WRF)能够输出包括大气要素、陆地要素、土壤要素、海洋要素等在内的206个气象要素[10],相对于高空探测方式获取的气象数据要素更加完善多样。但是影响弹道解算的气象要素如气压、虚温、风速及风向不能通过WRF直接输出,因此本文中利用WRF输出的气象要素进行转换后获取上述弹道解算所需的气象诸元。

2 数值天气预报及同化方法

2.1 数值天气预报流程

本文中基于WRF及WRFDA平台,同化NCEP ADP全球高空及观测天气数据,进而获取外弹道计算所需要的气象要素。数值天气预报的一般流程如图1所示。

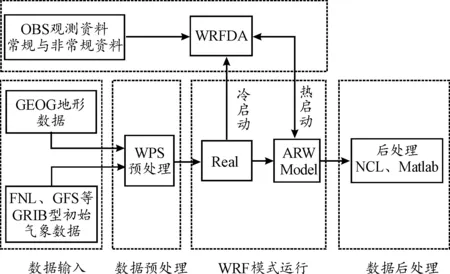
图1 数值天气预报流程图Fig.1 Flow chart of numerical weather forecast

数值天气预报包括数据输入、WPS预处理、WRF模式运行及数据后处理等4个部分。WPS模块整合地形数据和初始边界数据,将输入的大气数据进插值到对应的网格上,WRF模块实现对未来大气状态的预报,后处理模块使用NCL等软件对其输出数据进行处理,如插值绘图。

2.2 三维变分同化及气象诸元转换

图1中WRFDA负责资料同化工作,用于同化各种观测资料。数据同化一般有2种方案:一是使用REAL为同化生成初始条件,更新侧边界条件后进行预报,该方法称为冷启动;二是热启动,也称循环同化,从WRF的预报文件开始同化,更新下边界后进行同化,并更新侧边界后进行预报。目前资料同化方法有变分同化和Kalman滤波法等,由于三维变分法对计算机资料要求相对较低,能较为简单方便地同化各种新型的观测资料[11],因此本文中选用三维变分方法探究冷热启动2种同化方案对弹道解算用数值天气预报的影响。

变分同化的目的是:通过用模式的动力结构的约束来确定接近观测资料的模式的初始场,解的最优性可以用表示模式解和观测资料差异的目标函数来衡量[12]。可定义如下的目标函数为:

(3)

式中:x为大气分析场的状态向量;xb为背景向量;y0为观测向量;B为背景误差协方差矩阵,其水平协方差由递归滤波表示,垂直协方差由经验正交函数模拟;E为观测误差;F为观测算子的H的协方差矩阵;H为将模式分析变量变换到观测空间的观测算子。

在式(3)中,当J(x)中的x=xa时,取得最小值,即为分析值,有:

▽xJ(xa)=0

(4)

通过最小化目标函数及目标函数的梯度来调整初估场分析值,最后即可得适合模式的最优解。但是WRF输出的气象要素并非外弹道计算需要的气象条件,因此需要对输出的数据进行空间插值及格式转换[13]。WRF模式输出的变量可参见文献[14],其与外弹道诸元的转换关系为:

风速的值由纬向风U和经向风V合成确定,即:

(5)

风向的值由纬向风U和经向风V角度分解得到,即:

(6)

海拔高度的值由扰动位势高度PH和基准态位势高度PHB换算得到,即:

(7)

气压的值由扰动气压P和基准态气压PB换算得到,即:

p=P+PB

(8)

虚温的值由扰动气压P、基准态气压PB、扰动位温T和露点温度TD计算得到,单位为K,在弹道学当中虚温的计算公式为:

τ=(1+0.608q)·t

(9)

式中:q为气象学中的比湿,t为气象学中的气温。气温的值由扰动位温T、扰动气压P和基准态气压PB计算得到,有:

(10)

比湿q是湿空气中水汽质量与湿空气的总质量之比,可以通过水汽压E得到,有:

(11)

式(11)中,水汽压E是空气中水汽的分压强。本文当中选用的是改进马格纳斯(Magnus)经验公式计算得到,即:

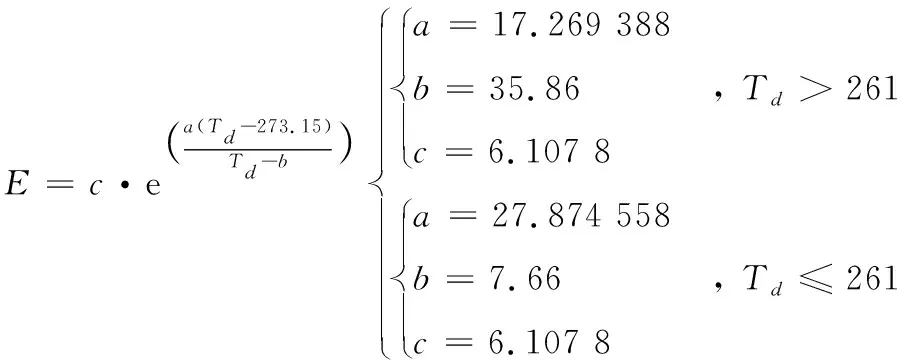
(12)

式(12)中,Td为露点温度,露点温度可以通过WRF模式直接输出。最后将式(10)—式(12)代入到式(9)中,可以得到外弹道计算中所需要的虚温的值。

2.3 弹道解算所用气象要素误差分析

对WRF输出的数据进行转换,对其能否应用于弹道解算,可以利用均方根误差和平均绝对误差来比较数值天气预报结果的误差大小和幅度[15]。

(13)

(14)

其中:每个格点样本高度层为i;样本第i个高度层的气象计算值为Fi;样本第i个高度层的实测气象值为Oi;每个高度层的权重系数为Wi。在不考虑炮射条件的情况下,假设各气象层的权重系数相等,即令W1=W2=…=Wn=1/n。

当CRMSE与CMAE联用时,可以判断数值模式是否存在较大误差。若2个值相差较大,表示模式存在较大误差,有一定的不稳定性;若2个值相近,则表示数值模式的误差分布相对均匀,则数值气象预报结果能够直接应用于弹道解算之中。

3 弹道计算与验证

以2022年夏季某日0点(世界时)开始预报为例,本文利用WRF预测数据及应用同化后的预测进行数值对比,相关参数条件及数据基础如下。① WRF模式预报区域为东北某地区,其中心坐标为北纬47.5°,东经124.5°,预报时间设置为12 h。模式水平方向上采用单重网格结构,格点数为121×121,格点间距为5 km,垂直方向上分为121层,模式顶层气压为1 000 Pa,积分步长为30s。② 陆面静态数据使用美国地质勘探局(USGS)提供的地形数据;初始边界数据使用NCEP发布的分辨率为0.25°×0.25°的GFS再分析资料;选取的观测资料为NCEP ADP全球高空观测天气数据;对比真值数据为中国国家高空气象站定时值观测资料。

3.1 资料同化对气象诸元的改进效果分析

对比同化前后的预报结果可以发现,利用观测资料对初始场进行调整后,预报结果的气压、虚温及风速都发生了改变。表1列出了气压、虚温、风速等3个要素观测值和模拟值之间的均方根误差及平均绝对误差。从表1中可看出,风速和虚温的MAE值和RMSE值接近,相关性强;气压MAE和RMSE的值相关性强,但存在一定差距,也说明气压数据存在一定系统误差。由此可见,数值天气预报结果中虚温和风速条件的误差较小,气压条件的误差相对较大但误差很稳定,能够适用于弹道解算中。

表1 3种预测结果与观测值之间误差分析Table 1 Error analysis between the three predict results and the observed values

图2—图5分别是气压、虚温和风速、风向在垂直方向上预测值与实测值的对比图。

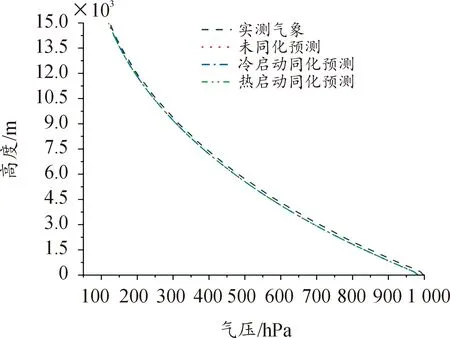
图2 3种预测及实测值在气压上的垂直分布Fig.2 Vertical distribution of three simulated and actual air pressures

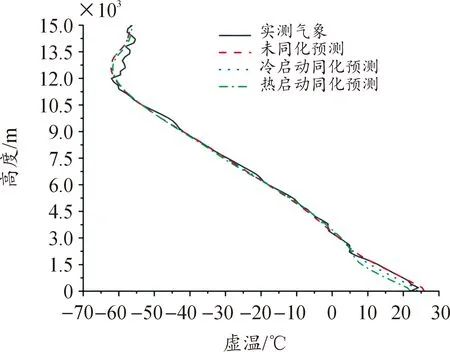
图3 3种预测及实测值在虚温上的垂直分布Fig.3 Vertical distribution of three simulated and actual temperatures

图4 3种预测及实测值在风速上的垂直分布Fig.4 Vertical distribution of three simulated and actual wind speeds

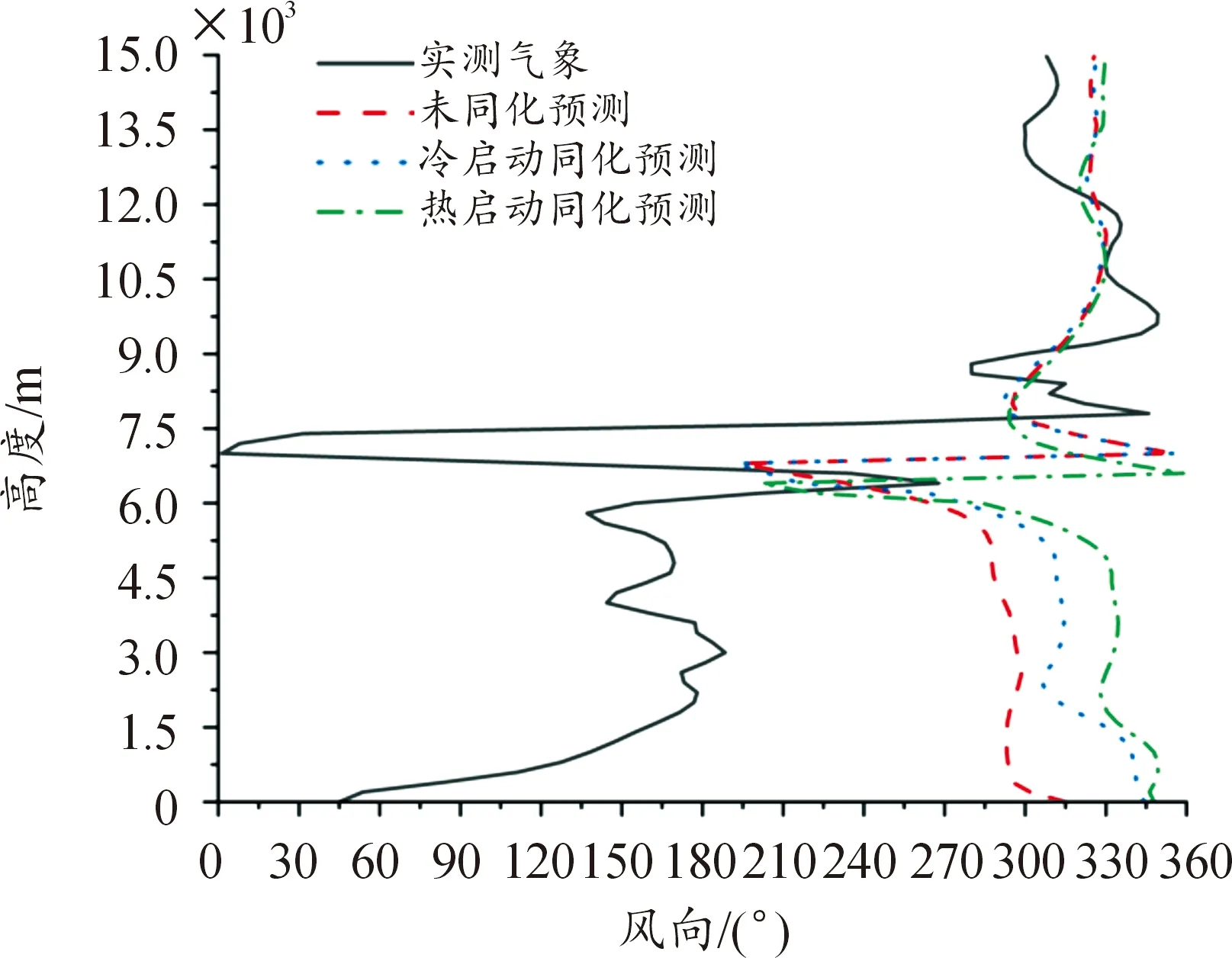
图5 3种预测及实测值在风向上的垂直分布Fig.5 Vertical distribution of three simulated and actual wind directions

从图2—图5中可看出,3种预测值在垂直方向上趋势一致,但与实测值有一定差距。同化试验对气压模拟改善不显著,预测值总体偏低;对温度而言,在2 km以下低空及12 km以上高空,预测值与实测值有所差异,预测值偏低,在其余高度,预测值与实测值接近;对风速而言,3种预测差别不大,但在不同高度上表现不同,低层冷启动同化预测预测值更接近观测值,随着高度的增加,热启动同化预测的优势显现更接近实测值;风向作为记录风吹来的气象要素,数值变化呈圆形循环,其360°变化的特征导致了风向预测的难度。同化试验对风向的预测效果较差,6 km以下低层3种预测值均与实测值偏离较大,随高度增加,预测效果逐渐接近实测值。

3.2 资料同化在弹道解算的应用效果分析

本文中利用WRF输出的气象数据进行弹道计算,并与该时刻实测弹道数据进行对比。实验炮射选用某口径榴弹,炮射条件为820 m/s的初速,47°的射角,0°的射向。弹道轨迹及弹道落点图如图6、图7所示。

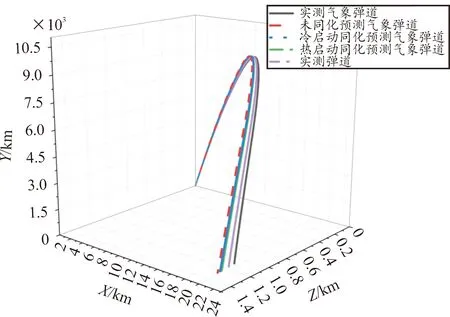
图6 弹道轨迹图

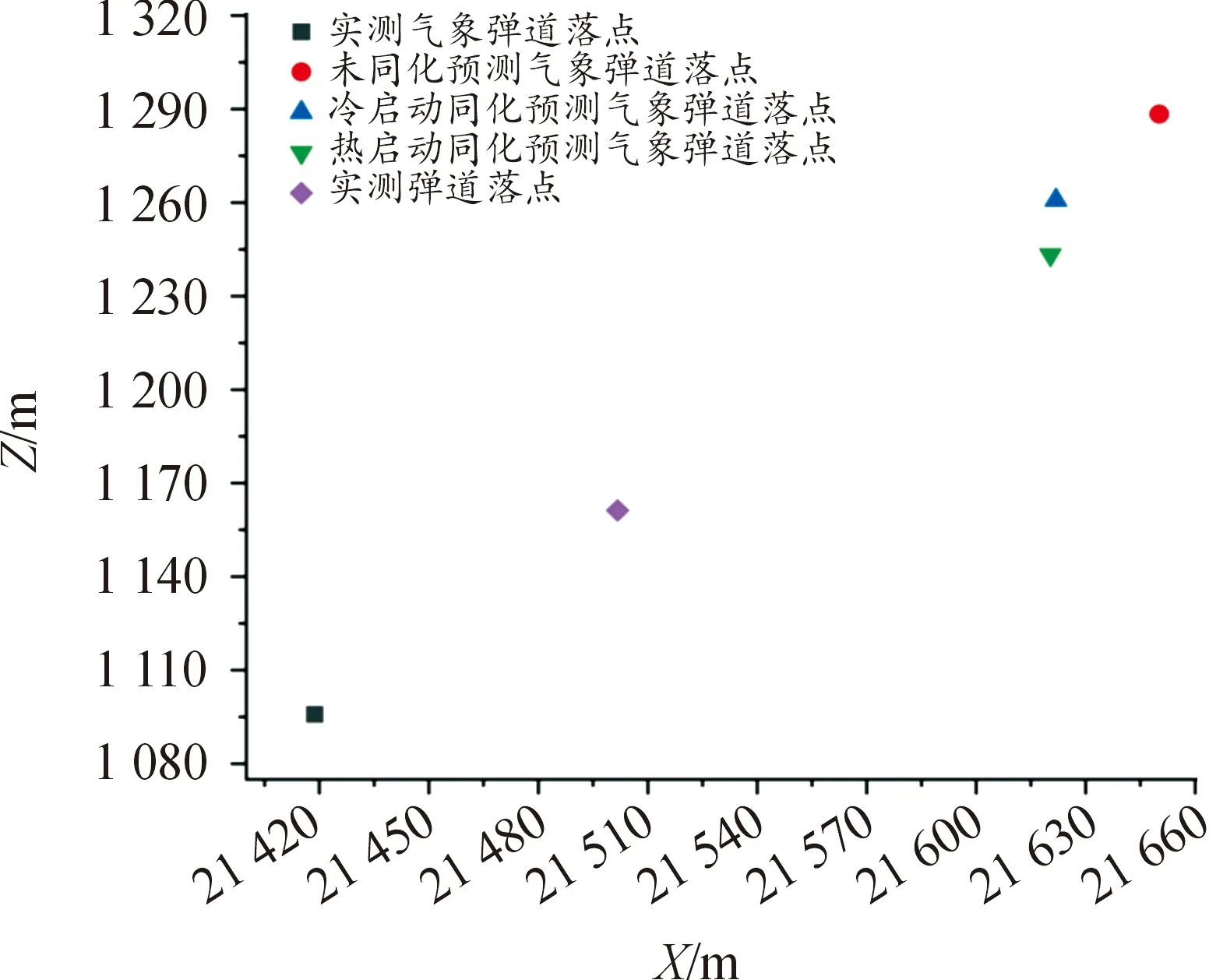
图7 弹道落点分布图Fig.7 Ballistic simulation landing point distribution

由图6、图7可以看出,4组弹道预测轨迹与实测弹道轨迹接近,其中实测气象弹道与热启动同化预测弹道落点最为接近实测弹道落点。由于弹道在末端的偏差较大,误差影响程度明显,故以降弧段弹道轨迹做放大对比分析,结果如图8所示。

图8 降弧段平面对比图Fig.8 Plane comparison of descending arc segment

为了更直观分析,表2列出了各预测弹道与实测弹道参数对比数据。表2中的“-”表示预测弹道比实测弹道更靠近炮位坐标原点。从表2可以看出:相比实测气象数据,应用数值天气预报对弹道落点的解算准确度仍有不足。在3条预测气象弹道中,应用热启动同化的气象预报结果弹道落点与实测落点更为接近。与应用未同化的数值预报的弹道计算相比,应用了热启动同化的数值预报的弹道计算X方向射程的预测相对误差减小了约0.14%,其与实测弹道的射程差为118 m;Z方向侧偏的预测相对误差减小了约3.89%,其与实测弹道的Z方向偏差为81 m,提升了数值预报应用于弹道解算的精度。

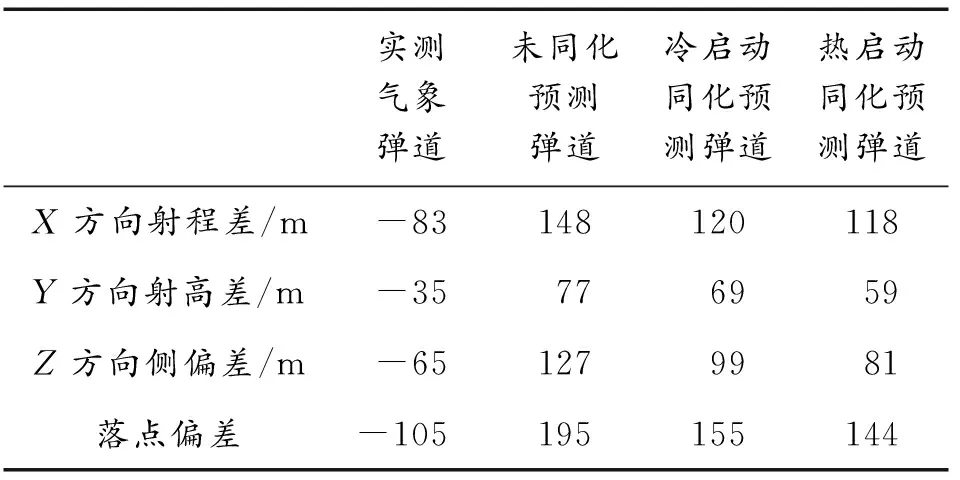
表2 弹道参数对比数据Table 2 Ballistic parameter comparison

4 结论

在弹道解算中,应用不同资料同化方法对气象预报结果的改进效果有所差异。数值天气预报在准确度上与实测气象有一定差距,但其在实时性上优于实测气象,能快速获取天气预报结果。本文中研究结果可以为提升弹道解算用数值天气预报的预报速度及准确度提供一定的理论参考。