首届宇宙新星选拔大赛开幕

大力

大赛组委会积极采纳群众意见，值得鼓励。但说实话，他们提供的两个方案，我根本没看出有啥区别呀！

失之毫厘，谬以千里！“推选一个星球”和“各选一个星球”涉及两种不同的计数原理。

加法原则

加法原则的核心是“分类”。假设事件A有m种产生方式，事件B有n种产生方式，则事件A或B则有m+n种产生方式。

乘法原则

乘法原则的核心是“分步”。完成一件事需要分成2个步骤，做第一步有a种方法，做第二步有b种方法，那么完成这件事共有 a×b 种方法。

我相信你们都听懂了吧？！

听懂了才怪……

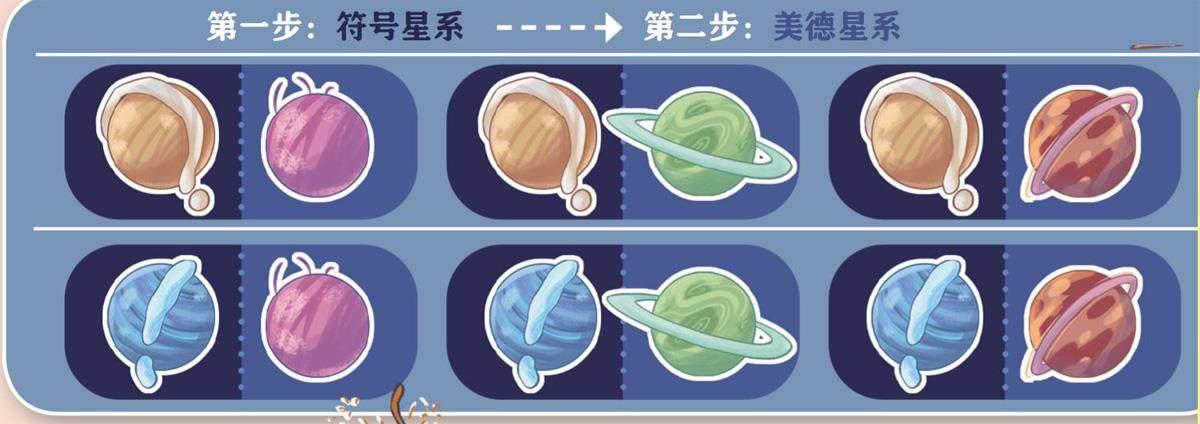
第一种方案是从两大星系中选取一个星球作为大奖得主。大家要么是从符号星系的2个星球里选，要么是从美德星系的3个星球里选。

大奖得主共有2+3种（即5种）可能，这种方案涉及加法原理。

那第二种方案呢？

第二种方案是从两大星系中各选一个星球作为大奖得主。大家需要分两步完成推选，因此会用到乘法原理。大奖得主共有以下6种可能：

画重点

有个简单的小技巧来区分两者，就是看看能不能一次性完成这件事，如果能一次性完成就用加法原则，不能就用乘法原则。

我好像悟到了！

比如我有2件深色外套、3件浅色外套，那么我就有5种选择方案。我只选1次就行，因此用加法原理。

如果我有2件上衣、3条裤子，那么我就有6种选择。因为我必须得用上衣搭配裤子，所以要选2次，因此用乘法原理。

孺子可教也！

到了中学，你们会接触到一个数学术语“排列组合”。我们刚才提到的“加法原理”和“乘法原理”就是排列组合的基础。

排列是什么呢？简单来讲，就是把事物排在一起，构成一列，计算共有多少种排法。组合呢，就是从整体中选取部分元素进行组合，然后计算有多少种组合方式。

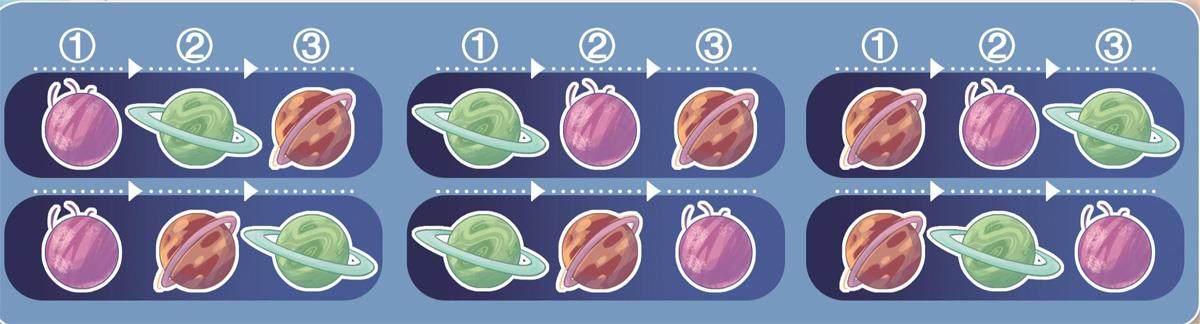
“有顺序”和“无顺序”是区别二者的重要准则，比如美德星系的组合只有1种，即聪明星球、善良星球和正义星球。但如果排列它们的出场顺序，就有6种可能：

很简单对不对？但我们在日常生活中常常发现更为复杂的情况：我们在做一件事情时，往往有几类不同的方法，而在每一类方法中，还要分步完成。那么，完成整件事情既要排列又要组合。

问题来了

假设出场节目有10个，分别是5个唱歌节目、3个舞蹈节目、2个相声节目，且舞蹈节目不能连续出场，那么一共能排出多少种出场顺序？

您说慢点儿……

要不我们一个个排？

哈哈哈，我被自己出的题难倒了，还是降低一下难度吧！让每个星球随便出一个节目，共有几种出场顺序呢？

解决这一问题我们用到的是乘法原理，出场顺序可能性共计5×4×3×2×1=120种。这是一个较为简单的排列问题。

为了增进宇宙民众的友谊，我们让这5个星球两两组合表演节目，那么又有多少种组合方式呢？

只要在1次选择中两两配对，就属于组队成功，因此我们用到的是加法原理，即有4+3+2+1=10种组队可能。这是一个较为简单的组合问题。

可怕的例题来了

1.在排5个星球的节目单时，问号星球和聪明星球作为承办方，必须出一个星球第一个表演节目，共有几种排节目单的方法呢？难度：★★★

2.为了更好地展示宇宙的精神面貌，每个星球各派出2名选手参赛。如果让这10名选手两两组合表演节目，那么共有多少种组合方式呢？难度：★★★★