镜片的棱镜效果与处方棱镜的计算方法探析

张丙寅　肖虹

众所周知，镜片由无数个棱镜组合而成。正球面透镜是由无数个基底相对的三棱镜旋转而成，且两者基底朝向光心；负球面透镜是由无数个顶相对的三棱镜旋转而成，且两者基底朝向边缘。透镜对光线的偏折作用称为透镜的棱镜效果，透镜上任意一点的棱镜效果就是位于该点所具有的棱镜度。在专业教学与实际工作中，视光师经常采用Prentice规则来计算棱镜度的大小[1～2]（如公式1）。

P=CF 公式1

在使用Prentice规则计算棱镜度时，为了让初学者更简易地掌握并判断棱镜度方向，可以将棱镜度和距离用矢量来表示，并对球面透镜、柱面透镜、球柱面透镜的棱镜效果进行矢量计算，从而能够通过符号判断棱镜方向。同时利用棱镜效果公式，进一步推导眼镜定配中制作移心棱镜时移心量的计算方法。

1 球面透镜的棱镜效果

如图1所示，计算球面透镜Q点的棱镜效果时，以光心O点为原点，建立直角坐标系，先确定Q点的坐标为（x，y），即视心在镜片的坐标位置。将Q点棱镜度作为矢量进行计算时，则应以Q点为原点，建立直角坐标系，Q点指向光心O点为距离矢量C，该矢量在坐标系中可以分解为水平分量CH和垂直分量CV，坐标为（-x，-y）。使用Prentice规则计算Q点的棱镜效果时，可以采用以下公式。

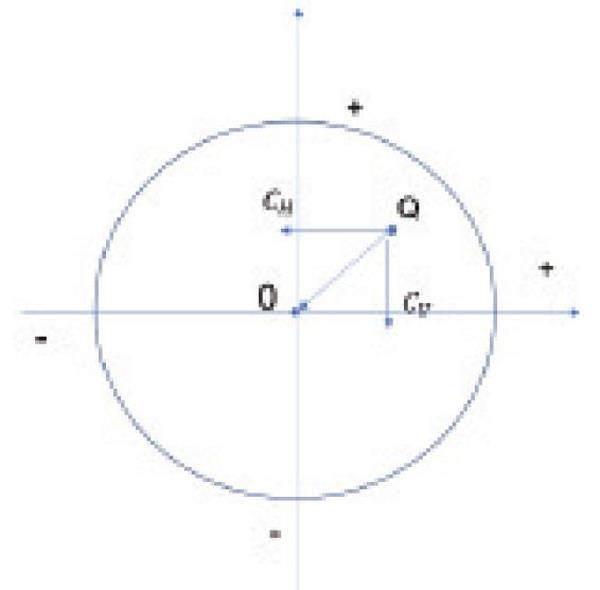
图1

P_H=C_HF=-xF 公式2

P_V=C_VF=-yF 公式3

注：P_H：Q点透镜棱镜屈光力的水平分量；P_V：Q点透镜棱镜屈光力的垂直分量；F：球面透镜的屈光力。

使用360°标示法来表示棱镜度方向，将360°标示法放在以Q点建立的直角坐标系里，从而计算得到P_V和P_H的数值，其符号含义如下所示：

P_H>0，底向0°；P_H<0，底向180°

P_V>0，底向90°；P_V<0，底向270°

使用视光学中棱镜基底4个基本方向（底向上BU、底向下BD、底向内BI、底向外BO）表示时，根据公式2、3可知，当计算的“-F”为正时，棱镜方向与x、y的坐标方向一致，当“-F”计算为负时，棱镜方向与x、y的坐标方向相反。

2 柱面透镜的棱镜效果

图2

如图2所示，由于柱面透镜轴向屈光力为0，轴上无棱镜，在垂轴方向屈光力最大，所以棱镜效果只发生在垂轴的方向[3]。计算柱面透镜Q点的棱镜效果时，以光心O点为原点，建立直角坐标系，确定Q点的坐标为（x，y），柱面透镜轴与x正半轴夹角为柱镜轴位β。根据几何关系，使用公式4计算Q点到柱面透镜轴的垂直距离。

C=y cosβ-x sinβ 公式4

计算Q点棱镜度时，以Q点为原点，建立直角坐标系，Q点到柱面透镜轴的垂直距离矢量在水平方向分量和垂直方向分量分别以公式5、6进行计算。

C_H=-（y cosβ-x sinβ）×cos（π/2+β）=（y cosβ-x sinβ）×sinβ=C sinβ 公式5

C_V=-（y cosβ-x sinβ）×sin（π/2+β）=-（y cosβ-x sinβ）×cosβ=-C cosβ 公式6

Q点到柱面透镜轴的垂直距离矢量表示为Csinβ、-Ccosβ，因此使用Prentice规则计算Q点的棱镜效果时，可以采用以下公式。

PH=CF sinβ 公式7

PV=-CF cosβ 公式8

注：PH：Q点透镜棱镜屈光力的水平分量；PV：Q点透镜棱镜屈光力的垂直分量；F：柱面透镜的屈光力。

使用360°标示法表示棱镜度方向，棱镜符号表示方法与球镜表示方法相同。使用视光学中棱镜基底4个基本方向（底向上BU、底向下BD、底向内BI、底向外BO）表示时，根据公式7可知，当Fsinβ、-Fcosβ为正时，棱镜方向与Q点的坐标方向x、y一致；当Fsinβ、-Fcosβ为负时，棱镜方向与Q点的坐标方向x、y相反。

通过公式7推导水平方向的棱镜度，可以得到以下两个公式。

P_H=CF sinβ=（y cosβ-x sinβ）×sinβ×F=-F×sin2β×x+F sinβcosβ×y 公式9

P_H=F×sin²β×x 公式10

由公式9可知，其与公式10计算水平方向棱镜度不同，这是因为公式10混淆了球面透镜和柱面透镜的棱镜效果计算方法[4]，柱面透镜的棱镜效果只能发生在垂轴方向，所以使用Prentice规则中的C也指的是Q点指向柱面透镜轴的垂直距离，因此，视光师在实际工作中使用公式9计算水平方向棱镜度更准确。

同理，通过公式8推导出垂直方向的棱镜度，如公式11所示。

P_V=-CF cosβ=-（y cosβ-x sinβ）×cosβ×F=-F×sinβcosβ×x+F cos2β×y公式11

3 球柱面透镜的棱镜效果

计算球柱面透镜的棱镜效果时，将球柱面透镜分解为球镜和柱镜的形式[5]进行计算后再求和，也可以将球柱面透镜分解为两个正交柱镜的形式进行计算后求和，计算出来的棱镜方向判断与球镜片相同。

P_H=-F_S×x+（y cosβ-x sinβ）×sinβ×F_C公式12

P_V=-F_S×y-（y cosβ-x sinβ）×cosβ×F_C公式13

注：F_S：球面透镜的屈光力；F_C：柱面透镜的屈光力。

4 移心棱镜的计算方法

在视光学理论中，根据处方棱镜大小，通过将镜片的光学中心移动到偏离瞳孔中心位置，从而在镜片视心位置产生棱镜效应，称为移心棱镜。

移心棱镜的水平和垂直方向的移动距离也是通过Prentice规则计算后得到。移动距离矢量以瞳孔中心为原点，即以视轴为原点建立直角坐标系，Q点指向光心的距离矢量C，其坐标表示为（x，y），可以发现该坐标与以光心O点建立坐标的数值相等，方向相反，再利用公式14、15计算后得到x、y的数值。

x=P_H/F 公式14

y=P_V/F 公式15

同理，斜轴球柱透镜移心棱镜以视轴为原点，建立直角坐标系，此时与以光心O点建立坐标的数值相等，方向相反，因此公式12、13可以变换为公式16、17。

P_H=F_S×x+（-y cosβ+x sinβ）×sinβ×F_C=F_C×sin²β×x-F_C×cosβ×sinβ×y  公式16

P_V=-F_S×y-（y cosβ-x sinβ）×cosβ×F_C=-F_C×sinβ×cosβ×x+F_C×cos²β×y公式17

令：

A=F_C×sin²β 公式18

B=F_C×cosβ×sinβ 公式19

C=F_C×cos²β 公式20

将公式18、19、20带入公式16、17，得到公式21、22。

x=（C×P_H+B×P_V）/F_C公式21

y=（B×P_H+A×P_V）/F_C公式22

计算斜轴球柱移心棱镜的移心量时，可以使用公式21、22推算得之。

需要注意的是，对于单纯斜轴柱面透镜，由公式7、8可知，水平方向棱镜与垂直方向矢量以及轴位存在以下关系（如公式23），从而得到C的大小，但由公式4无法推导出x、y的数值。如果轴位在水平或垂直方向上，则垂轴方向棱镜为0，距离为0，可以计算出移心量的大小。

P_H/P_H=-tanβ 公式23

5 结论

通过以上公式推导，对于镜片的棱镜效果和棱镜移心量的计算，笔者得出以下结论：

a. 可以利用公式2、3计算球面棱镜某一点的棱镜大小，并根据符号进行棱镜方向的判断；

b. 在实际工作中，视光师应使用公式9、11来计算斜轴柱面透镜的棱镜效果，而非使用公式10进行计算；

c. 计算移心棱镜移心量时，是以视轴为原点建立的直角坐标系，因此Q点指向光心的距离矢量C，其坐标与以光心为原点建立的直角坐标系的坐标方向相反；

d. 计算斜轴球柱移心棱镜的移心量时，推荐使用公式21、22进行计算；

e. 对于单纯斜轴柱面透镜形成的移心棱镜，很难通过公式确定x、y的数值。

参考文献

[1] 王静.棱镜眼镜棱镜度和棱镜基底取向检测方法的探讨[J].计量与测试技术，2009，36（05）：28-29+31.

[2] 朱嫦娥.移心棱镜眼镜的三种制作方法之比较分析[J].中国眼镜科技杂志，2020（09）：112-115.

[3] 张萍辉.快速确定三棱镜镜片的加工中心[J].中国眼镜科技杂志，2017（01）：101-103.

[4] 谢银月，李湘宁.自动焦度计定量计算式的研究[J].上海理工大学学报，2013，35（02）：161-164.

[5] 眼镜光学技术[M].人民卫生出版社，朱世忠，余红，2019.

作者单位：1.天津职业大学

2.天津市康视标准眼镜有限公司

本研究成果为天津市科技特派员入驻天津市康视标准眼镜有限公司时，与企业共同完成。由天津职业大学科学研究基金项目（项目编号：20181108）资助。