利用蒙特卡罗模拟评估医用电子直线加速器非均整模式的光子束软化特性
陈蕾 李长虎 傅玉川 韩纪锋


摘要:本文利用蒙特卡罗模拟评估不同能量、不同射野下医用电子直线加速器非均整模式(Flattening Filter Free, FFF)光子束的软化特性. 基于本院的Varian Edge加速器的组件参数和测量数据,利用通用蒙卡程序EGSnrc/BEAMnrc构建6 MV均整模式(Flattening Filter, FF)、6 MV FFF和10 MV FFF下的机头模型,使用EGSnrc/DOSXYZnrc程序模拟获得5 cm×5 cm和10 cm×10 cm射野下的百分深度剂量(Percentage Dose Depth, PDD)和横向剂量离轴比(Off Axis Ratio, OAR),与测量数据进行比较,确定不同模式的源参数;在此基础上模拟三种光子束模型在上述两种射野射野条件下非均匀模体(水-骨-肺-水)内的PDD,并对其相空间文件进行能谱分析,评估FFF光子束的软化特性. 三种光子束模式在非均匀模体内的PDD趋势相似,但在小野时扰动更大,FFF模式相较于FF模式,包含更多的低能光子和更少的机头散射;在低能、小野时,6 MV FFF模式的光子束软化特性带来的剂量影响与6 MV FF模式相比并不明显,但在高能、大野时,光子束软化特性逐渐明显. 相对于FF模式,FFF光子束具有更陡峭的剂量跌落,尤其在小野、低能时,使其在临床治疗上具有明显的优势;但在大野、高能时,FFF光子束出现明显的软化特性,尤其是在低密度区,需要谨慎考虑临床计划方式的选择.
关键词:光子线;蒙特卡罗模拟;非均整模式;EGSnrc;能谱;射束软化
收稿日期: 2023-03-03
基金项目: 四川大学华西医院临床新技术项目(医临新2021-314号);四川省科技计划重点研发项目(2020YFS0274)
作者简介: 陈蕾 (1998- ),女,四川资阳人,硕士研究生,主要研究辐射物理与医学物理. E-mail: chenlei2020@stu.scu.edu.cn
通讯作者: 傅玉川. E-mail: ychfu@hotmail.com
Evaluation of photon beam softening characteristics in flattening-filter-free mode of medical electron linear accelerator by Monte Carlo simulation
CHEN Lei1,2, LI Chang-Hu1, FU Yu-Chuan1, HAN Ji-Feng2
(1. Radiotherapy Physics & Technology Center, Cancer Center, West China Hospital, Sichuan University, Chengdu, 610041, China;2. Key Laboratory of Radiation Physics and Technology, Ministry of Education; Institute of Nuclear Science and Technology, Sichuan University, Chengdu 610064, China)
Monte Carlo simulations were used to evaluate the photon beam softening characteristics of medical electron linear accelerators operated in flattening filter-free mode (FFF)under different energies and field sizes. Using the parameters of the Varian Edge accelerator and measured data in our hospital, a 6 MV flattening filter (FF), a 6 MV FFF, and a 10 MV FFF model in the accelerator head were constructed using the general Monte Carlo program EGSnrc/BEAMnrc. Using EGSnrc/DOSXYZnrc, three modes were characterized based on percentage depth dose (PDD)and off-axis ratio (OAR), which were compared with simulation data to determine source parameters. By using the above models, we obtained PDDs for three modes of inhomogeneous phantoms (water-bone-lung-water)in two field sizes, and the energy spectrum was calculated from phase space files, then the FFF photon beam softening properties were analyzed. In the inhomogeneous phantom, the PDD trends of the three photon-beam modes are similar, but the fluctuations are greater at small fields. In contrast to FF mode, FFF mode contains more low-energy photons and less head scattering. At low energy and small field, photon beam softening caused by the 6 MV FFF mode does not bring about a noticeable dose effect, however, at high energy and large field, the beam softening effect is gradually apparent. FFF photon beams have a steeper dose drop than FF beams, especially at small fields and low energy, which makes them evidently advantageous in clinical settings; however, at large fields and high energies, FFF photon beams appear to have significant softening characteristics, particularly in low-density areas, requiring careful consideration of the choice of clinical planning modality.
Photon beam; Monte Carlo simulation; Flattening filter free; EGSnrc; Energy spectrum; Beam softening
1 引 言
传统的医用电子直线加速器中,均整器(Flatten Filter, FF)是初级准直器和监测电离室之间的重要组成部分,可以使射束产生均匀的注量. 然而,随着逆向计算和更加适形的放疗技术的出现[1],如调强放射治疗(Intensity-modulated radiation therapy, IMRT)和立体定向放射治疗(Stereotactic Radiosurgery, SRT),FF已经不再是必要的[2]. 较多的医用电子直线加速器已经提供了非均整(Flatten Filter Free, FFF)模式,如Varian TrueBeam、Elekta Versa HD和Siemens Artiste等. 相比于FF光束,FFF光束具有不同的光束轮廓、光子能量光谱和头部散射特性等[3].
蒙特卡罗(Monte Carlo, MC)算法[4]是一种被广泛认可的准确的剂量计算方法,适用于复杂加速器和患者模型的计算. 尤其是在复杂患者几何形状和组织异质性的情况下,MC算法表现出其优势[5]. 针对不同能量下FFF模式的剂量学特性已经有较多研究[6-9].这些研究表明,FFF模式可以提高剂量率,减少头部散射和中子污染,改善野外剂量和减小半影大小.而这些特性与射束的软化密切相关. 除此之外,由于去除FF后,FFF模式的光子能谱发生改变,商用计划系统的剂量算法也需要对这种不均匀性进行校正[10,11]. 然而,目前对于FFF模式光子束软化特性的分析和评估的研究还较为有限.
本文旨在基于四川大学华西医院Varian Edge加速器的组件参数和测量数据,使用通用MC程序EGSnrc内包含的BEAMnrc/DOSXYZnrc软件包[12]构建6 MV FFF模式、6 MV FF模式和10 MV FFF模式下的加速器模型,计算它们在非均匀模体内的剂量沉积,并进行能谱分析,评估和比较不同射野和不同能量下医用电子直线加速器FFF光束的软化特性.通过以上研究,人们可以更好地理解光子线的物理特性.这为临床计划设计和剂量学比较提供了参考.
2 材料与方法
2.1 医用电子加速器MC模型构建
基于EGSnrc的软件包BEAMnrc/DOSXYZnrc
对6 MV FF模式、6 MV FFF模式和10 MV FFF模式的光子束进行模拟. 加速器机头中各组件及参数参考Varian官方数据库和Varian Edge加速器. 为建立准确的MC模型,辐射源需要选择合适的射束能量、光斑大小和平均角展[13,14]. 模型的源参数选择,通过不断试错调整后获得,具体流程如下.
首先,使用BEAMnrc程序模拟医用直线加速器的头部和光子束. 图1显示了6 MV FF模式的MC模型,其中包括靶、初级准直器、真空窗出口、均整器、监测电离室、灯光野镜和次级准直器等组件.FFF模型将FF去除,6 MV FF模式和10 MV FFF模式分别以一块0.2 cm和0.8 cm厚的铜片替代[3,15]. 6 MV FFF模型和6 MV FF模型的靶设置相同,为铜和钨共同组成,而10 MV FFF模型的靶为更厚的单一的铜,其余组件设置相同. 分别模拟获得三个模型在射野尺寸(Field Size)为5 cm×5 cm和10 cm×10 cm,距离辐射源100 cm处的相空间文件. 对于所有模拟,运行获得包含约1×109个粒子数的相空间文件.
然后,使用DOSXYZnrc计算源皮距(Source to Surface Distance,SSD)100 cm时,48 cm×48 cm×35 cm均匀水模体内的剂量分布,体素大小为0.2 cm×0.2 cm×0.2 cm. 由BEAMnrc生成的相空间文件将被用作DOSXYZnrc程序中的粒子源,模拟粒子数均为1×109,未重复使用相空间文件,其他参数设置与BEAMnrc程序一致.
最终获得三个光子束模型在两个射野下的百分深度剂量(Percentage Depth Dose, PDD)曲线与离轴比(Off-Axis Ratio, OAR)曲线,其中PDD均在最大剂量点归一化,OAR在中心轴处归一化. 然后与测量数据比较验证,当差异在临床可接受范围内时,确定为最佳模型,具体比较方法参考2.3.
2.2 使用非均匀模体的模拟设置
参考Onizuka等人[16]设计的非均匀模体来评估射束软化. 设置非均匀模体沿z方向包括四个部分:水 (4 cm),骨组织 (2 cm),肺组织 (5 cm)和水 (24 cm).x和y方向尺寸大小一致,非均匀模体尺寸为24 cm×24 cm×48 cm,如图2所示. 利用通过模拟验证后获得的三个光子束模型的相空间文件作为DOSXYZnrc程序的入射源,模拟在该模体下的剂量沉积,获得PDD曲线进行比较.z方向体素尺寸为0.2 cm,x和y方向的体素大小随模拟射野大小调整以提升模拟效率.模拟粒子数均为1×109,不确定性小于0.5%.
2.3 MC模型验证与数据分析方法
基于相同尺寸的三维水箱,采用灵敏体积0.125 cc的电离室探测器测量了Varian Edge加速器三种光子束模式在上述两个射野下,SSD 100 cm时的PDD和深度为10 cm时的OAR,与MC模拟结果通过局部剂量百分偏差进行比较,验证模拟的准确性[17],如式(1)所示.
ΔD=(Dsim-Dref)/Dref×100 (1)
其中,ΔD为局部剂量百分偏差;Dsim是通过MC模拟计算的剂量;Dref则是通过参考方法或测量获得的剂量. 具体模型验证结果参考3.1.
然后,获得三种光子束模式在非均匀模体内不同射野下的PDD曲线,并用EGSnrc/BEAMDP程序对6 MV FF模式和6 MV FFF模式的相空间文件处理,获得能谱和注量分布,分别以最大值为标准,进行归一化处理.
2.4 MC模拟一般参数设置
在BEAMnrc程序和DOSXYZnrc程序中的一般MC参数设置一致. 光子和电子截止能量分别设置为0.01 MeV (PCUT)和0.7 MeV (ECUT),电子截断值设置为2 MeV (ESAVE),电子步长算法为PRESTA-II,电子边界算法为PRESTA-I. 并且,采用了方差减少技术,采用轫致辐射方向分裂(Directional Bemsstrahlung Splitting, DBS)方法增加计算效率[18],分裂数为1000,分裂直径与射野大小一致. 模拟在个人计算机上进行,配置为:操作系统Ubuntu 20.04.5 LTS x86_64, CPU型号Inter core i7-10700 (16)@ 4.8 GHz,GPU型号NVIDIA GeForce GT 730.
3 结 果
3.1 MC模型验证
为了获取完整加速器模型的源参数,需要先调节入射电子能量,然后再调节光斑大小,最后调整射束平均角展. 在光斑大小调整过程中,为了简化模拟,将x和y两个方向的半高全宽(Full Width at Half Maximum, FWHM)设置为一致.
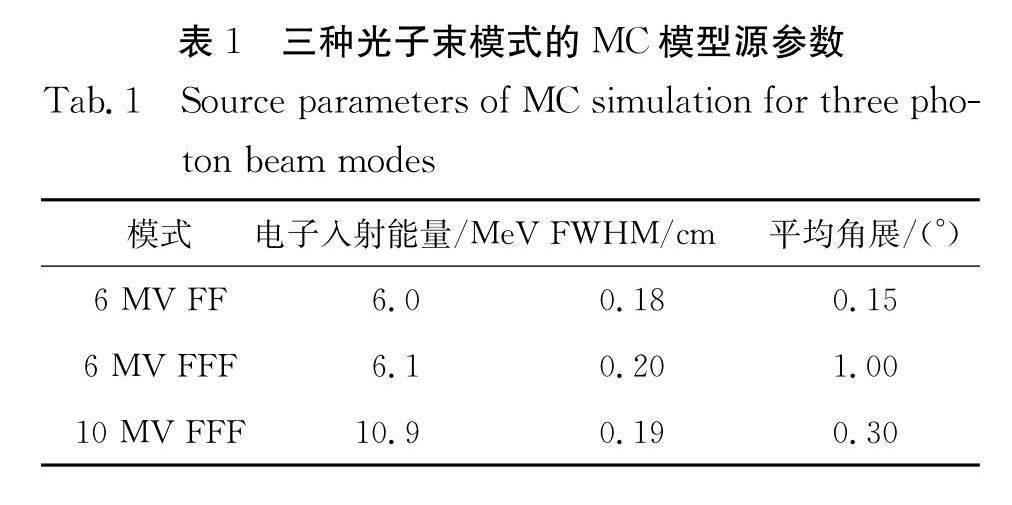
对三个光子束模型的源参数进行调整,直到与水箱测量数据具有一致性,最终源参数如下表1所示. 图3和图4分别展示了三个光子束模型模拟获得的PDD、OAR曲线与测量值的比较. 结果表明,模拟数据与测量数据之间具有较好的吻合度,PDD的百分偏差均小于5%,OAR平坦区的百分偏差均小于1%,都在临床可接受范围内. 10 cm×10 cm射野条件下,三个光子束模型的D20/D10的模拟值与测量值的百分偏差分别为0.96%(6 MV FF)、0.2%(6 MV FFF)和1.0%(10 MV FFF). 因此,可以得出结论,MC模型的构建是准确可靠的.
3.2 三种光子束模式在非均匀模体内的PDD
图5展示了三种光子束模式在非均匀模体内5 cm×5 cm和10 cm×10 cm射野内的PDD,以及6 MV FF模式和6 MV FFF模式PDD的绝对差异,重点关注了它们在剂量建成区的表现和不同深度的PDD差异. 结果表明,在两种射野下,三种光子束模式的PDD都呈现出相似的变化趋势,即在进入骨组织之前呈上升趋势,离开骨组织后呈下降趋势,但在小野(5 cm×5 cm)时还可以看到PDD在从肺组织进入水之后,有轻微的上升趋势.
相比于6 MV FFF模式,6 MV FF模式的PDD曲线始终更高,二者的最大剂量点位置相近,分别为1.3 cm(6 MV FFF)和1.5 cm(6 MV FF). 在剂量建成区,可以发现6 MV FF模式的表面剂量低于6 MV FFF模式,在10 cm×10 cm射野深度1 mm处分别约为50.25%(6 MV FFF)和40.95%(6 MV FF). 随着深度的增加,可以观察到6 MV FF模式水-骨和骨-肺交界面的PDD差异更大. 同时,随着射野逐渐增大,6 MV FFF模式相对于6 MV FF模式的PDD差异也逐渐明显.在离开骨组织后,在10 cm×10 cm射野内,二者的差异更加明显.
相比于6 MV FFF模式,10 MV FFF模式的PDD曲线更加曲折,其最大剂量点位于2.2 cm,比6 MV FFF模式更深,但其表面剂量更低,在10 cm×
10 cm射野深度1 mm处约为36.12%. 当剂量达到骨组织和肺组织后,可以看到10 MV FFF模式的PDD更加明显的跌落,其下降的斜率比6 MV FFF模式更大,并且在进入水组织后,5 cm×5 cm射野内的PDD上升更加明显.
3.3 FF模式和FFF模式的能谱比较
图6展示了在SSD 100 cm处,6 MV FF模式和6 MV FFF模式在5 cm×5 cm和10 cm×10 cm射野下的相对能谱和能量注量分布. 可以发现,6 MV FFF模式的相对能谱分布在两个射野下基本一致,并且具有更多的低能光子分布,特别是在低能量(<1.1 MeV)下. 当射野增大时,低能光子比例会轻微增加. 但6 MV FF模式的能谱在射野增大后,会发生右移,并且可以看到在5 cm×5 cm射野下的高能光子注量略高于10 cm×10 cm射野.
4 分析与讨论
通过对6 MV FFF模式和6 MV FF模式能谱的分析,可以发现去除FF后,FFF模式中低能光子增加,高能光子减少,射束的平均能量更低,会出现更软和峰值更靠前的能谱. 随着射野的增大,光子的横向散射增加,从而导致低能光子的增加. 相比之下,FF模式中机头散射随着射野的增大而增加,导致高能光子逐渐减少,低能光子增加[19]. 这种区别会导致FFF模式的剂量梯度更陡峭,剂量累积区域的剂量下降更快. 虽然在6 MV FFF模式下更多剂量沉积在表面,表面剂量增加,但随着射束能量的增加,这种陡峭的剂量梯度会破坏带电粒子的横向平衡,从而导致表面剂量的低估. Fogliata等人[20]也观察到相同的表面剂量趋势.
在均匀介质中,光子束的剂量分布相对均匀,但在非均匀介质中,如患者身体,横向平衡可能无法完全建立,特别是在不同组织之间的界面处[21,22]. 因此,采用非均匀模体可以更明显地观察到光子束的软化特性. 在骨组织和水的交界处,PDD迅速上升,可能是高能光子束会产生大量低能后向散射电子和缺乏带电粒子平衡[23,24],使得水中的剂量增加. 此外,在骨组织中,由于FFF束中缺少FF,会加剧高Z材料的对剂量沉积的影响,因此可以观察到FFF模式的PDD跌落更加明显,特别是在10 MV FFF模式中. 在骨组织和肺组织的交界处,浅层的骨组织会有较高的PDD,因为在肺组织内带电粒子的横向平衡更难达到,这会导致骨-肺交界处出现较大的差异. 然而,当射野较大时,由于散射和横向平衡效应的增加,这些差异会逐渐减小. 而在肺组织内,带电粒子的横向平衡不足,导致剂量显著降低,因为在肺组织中产生的电子范围比本研究中所定义的体素长度更长,导致很多电子将剂量沉积在射野之外. 并且,在采用FFF光子束时,由于较少的机头散射,随着射野的增大,光束软化的效应变得更加明显,导致其PDD相比于FF模式更低,并且在高能中更加明显. Teke等人[25]和Onizuka等人[16]在其MC模拟的 PDD曲线中观察到了同样的趋势.
光子束软化效应是放射治疗中必须考虑的重要因素.它会影响剂量计算和目标体积中的剂量分布,同时还会影响组织的放射生物学反应. 因此,治疗计划中考虑光束软化效应是非常重要的. 对比不同光子束在非均匀模体内的剂量沉积,发现6 MV FFF模式和6 MV FF模式在非均匀模体内的剂量沉积差异在小野范围内并不明显. 因此,在进行小野治疗时,6 MV FFF模式具有较少的机头散射,快速的剂量跌落,尤其是在进行SBRT治疗时,可以在保证治疗效果的同时,对危及器官有更好的保护. 但在较大射野和高能时,光子束软化更加明显,在非均匀模体内的剂量沉积与FF模式相比也有明显差异,尤其是在低密度区域. 因此,在制定临床计划时,需要仔细考虑对FFF模式的使用,包括射野大小与能量的选择.
5 总 结
本文采用能谱分析和MC模拟方法,研究了医用电子直线加速器中6 MV FF、6 MV FFF和10 MV FFF模式在非均匀模体内的剂量沉积,并评估了FFF光子束在不同能量、不同射野和不同介质下的软化特性. 研究结果表明,相对于FF模式,FFF光子束具有更快的剂量跌落,尤其在小野、低能时,优势更加明显. 然而,在大野、高能时,FFF光子束的软化特性更加明显,尤其在低密度区,需要谨慎考虑临床计划方式的选择.
参考文献:
[1]Cho B. Intensity-modulated radiation therapy: a review with a physics perspective [J]. Radiat Oncol J, 2018, 36: 1.
[2]Georg D, Kn??s T, McClean B. Current status and future perspective of flattening filter free photon beams [J]. Med Phys, 2011, 38: 1280.
[3]Xiao Y, Kry S F, Popple R, et al. Flattening filter-free accelerators: a report from the AAPM therapy emerging technology assessment work group [J]. J Appl Clin Med Phys, 2015, 16: 5219.
[4]邓力, 李刚. 粒子输运蒙特卡罗模拟现状概述[J]. 计算物理, 2010, 27: 791.
[5]Popescu I A, Shaw C P, Zavgorodni S F, et al. Absolute dose calculations for Monte Carlo simulations of radiotherapy beams [J]. Phys Med Biol, 2005, 50: 3375.
[6]韩俊杰, 陈立新, 朱金汉, 等. Varian Edge均整和非均整模式下6 MV和10 MV光子线能谱研究[J]. 中国医学物理学杂志, 2018, 35: 997.
[7]Feng Z, Yue H, Zhang Y, et al. Monte Carlo simulation of beam characteristics from small fields based on TrueBeam flattening-filter-free mode [J]. Radiat Oncol, 2016, 11: 30.
[8]Sushma N, Kaginelli S, Palanivel S, et al. Verification of surface dose for flattening filter and flattening filter free beams in beam-matched medical linear accelerators[J]. Asian Pac J Cancer Prev, 2021, 22: 2577.
[9]Kajaria A, Sharma N, Sharma S, et al. Monte Carlo study of unflattened photon beams shaped by multileaf collimator [J]. J Biomed Phys Eng, 2019, 9: 137.
[10]Robinson J, Opp D, Zhang G, et al. Evaluation of inhomogeneity correction factors for 6 MV flattening filter-free beams with brass compensators [J]. J Appl Clin Med Phys, 2013, 14: 3990.
[11]Muralidhar K R, Pangam S, Srinivas P, et al. A phantom study on the behavior of Acuros XB algorithm in flattening filter free photon beams [J]. J Med Phys, 2015, 40: 144.
[12]Kawrakow I, Walters B R B. Efficient photon beam dose calculations using DOSXYZnrc with BEAMnrc[J]. Med Phys, 2006, 33: 3046.
[13]Almatani T, Hugtenburg R, Smakovs A. A Monte Carlo model of an agility head for a 10 MV photon beam [J]. J Taibah Univ Sci, 2022, 16: 300.
[14]韩俊杰, 庄永东, 刘小伟. 医用直线加速器入射电子束能量的快速模拟确定[J]. 核技术, 2020, 43: 15.
[15]Kry S F, Vassiliev O N, Mohan R. Out-of-field photon dose following removal of the flattening filter from a medical accelerator[J]. Phys Med Biol, 2010, 55: 2155.
[16]Onizuka R, Araki F, Ohno T, et al. Accuracy of dose calculation algorithms for virtual heterogeneous phantoms and intensity-modulated radiation therapy in the head and neck [J]. Radiol Phys Technol, 2016, 9: 77.
[17]Kry S F, Titt U, Ponisch F, et al. A Monte Carlo model for calculating out-of-field dose from a Varian 6 MV beam [J]. Med Phys, 2006, 33: 4405.
[18]Shanmugasundaram S, Chandrasekaran S. Optimization of variance reduction techniques used in EGSnrc Monte Carlo codes [J]. J Med Phys, 2018, 43: 185.
[19]Javedan K, Feygelman V, Zhang R R, et al. Monte Carlo comparison of superficial dose between flattening filter free and flattened beams [J]. Phys Med, 2014, 30: 503.
[20]Fogliata A, Fleckenstein J, Schneider F, et al. Flattening filter free beams from TrueBeam and Versa HD units: evaluation of the parameters for quality assurance [J]. Med Phys, 2016, 43: 205.
[21]Yani S, Rhani M F, Haryanto F, et al. Inhomogeneity effect in Varian Trilogy Clinac iX 10 MV photon beam using EGSnrc and Geant4 code system[C]. Beijing: The 6th Asian Physics Symposium (APS), 2015.
[22]Siebers J V, Keall P J, Nahum A E, et al. Converting absorbed dose to medium to absorbed dose to water for Monte Carlo based photon beam dose calculations [J]. Phys Med Biol, 2000, 45: 983.
[23]Chow J C L, Owrangi A M. A surface energy spectral study on the bone heterogeneity and beam obliquity using the flattened and unflattened photon beams [J]. Rep Pract Oncol Rad, 2016, 21: 63.
[24]Reynaert N, Crop F, Sterpin E, et al. On the conversion of dose to bone to dose to water in radiotherapy treatment planning systems [J]. Phys Imag Radiat Oncol, 2018, 5: 26.
[25]Teke T, Duzenli C, Bergman A, et al. Monte Carlo validation of the TrueBeam 10XFFF phase-space files for applications in lung SABR [J]. Med Phys, 2015, 42: 6863.
[26]Murakami Y, Magome T, Matsubayashi F, et al. Evaluation of organ-at-risk dose reduction with jaw tracking technique in flattening filter-free beams in lung stereotactic body radiation therapy [J]. Phys Med, 2019, 61: 70.
[27]Wu J X, Song H C, Li J, et al. Evaluation of flattening-filter-free and flattening filter dosimetric and radiobiological criteria for lung SBRT: a volume-based analysis [J]. Front Oncol, 2023,13: 1108142.
引用本文格式:
中 文: 陈蕾, 李长虎,傅玉川, 等. 利用蒙特卡罗模拟评估医用电子直线加速器非均整模式的光子束软化特性[J]. 四川大学学报: 自然科学版, 2023, 60: 064003.
英 文: Chen L, Li C H, Fu Y C, et al. Evaluation of photon beam softening characteristics in flattening-filter-free mode of medical electron linear accelerator by Monte Carlo simulation [J]. J Sichuan Univ: Nat Sci Ed, 2023, 60: 064003.

