基于时间序列分析的环境γ辐射剂量率数据预处理方法研究及评估

白帆　李雪贞　马国学等

关键词：数据预处理;环境γ 辐射剂量率;时间序列;特殊数据检测;LSTM

中图分类号：X830. 3 文献标识码：A

辐射环境质量数据来源于多种监测设备，由环境γ 辐射剂量率数据、气象数据及各类监测数据等共同组成时序多元数据集。这些传感器连续数据间隔时间短，因此在短期内数据规模极大且含有噪音，由于传统的手工数据清洗方法成本高、效率慢，因此基于时间序列的数据预处理方法成为研究的热点。

与此同时，特殊数据检测也是数据挖掘的重要部分。特殊数据是指与其他数据分布有较为显著不同的数据对象，也被称作离群点，我们通常可以通过检测离群点得知离群点产生的因素，精确的数据可以帮助我们更有效地对特殊数据进行检测及分析，提高检测效率。

早在19 世纪，统计学家就已经对检测数据中的特殊数据值展开了研究，并随着时间的推移，研究出多种基于统计的特殊数据检测技术。常见的有3 倍标准差准则、箱线图等传统统计方法，以及由Box 和Jenkins 于20 世纪70 年代初提出的自回归移动平均模型、由Facebook 提出的Prophet 模型等时间序列预测方法[1] 。随着机器学习的不断发展，许多基于传统机器学习的方法被提出，例如基于二元线性的支持向量机、基于决策树的随机森林、基于距离的K-最近邻、具有噪声的基于密度的聚类方法、局部离群因子检测方法等聚类模型[2] ，Dorothy Denning 在1986年提出了第一个入侵检测系统的特殊数据检测模型，通过机器学习来进行特殊数据检测的方法被广泛应用。而当前主流的特殊数據检测算法通常基于深度学习技术，按照使用的监督信息可以分为有监督方法、无监督方法、半监督方法。例如自动编码器、生成式对抗网络[3] ， 长短期记忆网络[4] （LSTM） 等。有监督模型通常根据现有特殊数据标签学习，对数据更为精确地进行预测分类。由于LSTM 具有学习长期依赖关系的能力，可以更好地适应多元时间序列数据，本文主要探究有监督LSTM 的特殊数据检测模型。

本文涉及的数据类型包括γ 辐射剂量率数据及气象数据，以某地区某时段γ 辐射剂量率的逐时数据为例，研究数据预处理方法对特殊检测结果带来的影响，将详细介绍使用到的数据预处理技术，包括：辐射剂量率数据和气象数据的解析、数据频率的转换、时序数据去噪、剂量率数据及气象数据的完善、数据标准化处理等，并利用基于LSTM 的有监督特殊数据检测算法对数据预处理的结果从准确率、精确率、召回率、F1-分数方面进行评估，进一步提升辐射自动监测数据的筛选与优化。

1 数据预处理

为确保γ 辐射剂量率数据反馈的准确性，更加可靠真实地反应地区辐射环境水平，我们从数据的分析目标出发，通过探究数据分布、应用数据去噪、数据清洗及数据变换等数据预处理方法[5-6]消除原始数据中可能存在的测量噪声等造成的误导监测，为最终算法提供优质数据，使得其成为使算法发挥最佳性能的必要部分。

1. 1 数据分析

监测传感器数据是时间序列数据的典型实例。对数据进行统计学分析，通过计算平均值、标准差、峰值、偏度等统计值和数据正态分布的拟合情况来了解辐射剂量率数据的统计特征及分布状态，以便于根据数据特性选择合适的数据预处理方法，并分析时间序列数据背后隐藏的信息，理解序列模式的行为。

1. 2 数据集成

1. 2. 1 合并剂量率数据与气象数据 根据气象探测器与剂量率探测器地理位置坐标，将同一区域的气象监测数据与剂量率监测数据对应时间索引相结合，完善数据，便于结合剂量率与气象数据相关性进行分析及数据挖掘。

1. 2. 2 填充时间序列

检查时序数据是否为等间隔数据，依据原始数据时间索引间隔（30 s） 填充时间戳，缺失数据用空值暂时填充，删除重复时间戳。

1. 3 数据清洗

1. 3. 1 改变变量类型

时间序列是一组按照时间发生先后顺序进行排列的数据点序列。本文所处理的数据均基于时间序列，这里将原始数据索引规范为时间序列，并对变量（剂量率、电池电压、γ 辐射监测仪高压、温度、湿度、气压、雨量、风向、风速、感雨） 的数据类型进行转换，其中湿度与风向属于离散变量、感雨为分类变量（二值变量）、其他均为连续变量，为便于对数据进行分析及后续检测工作，统一转换为浮点数。

1. 3. 2 规定数据范围

本文所使用到的数据集为辐射剂量率数据与对应同步时间的气象数据，由于人为因素及自然因素均会引起剂量率数值的变化，因此在对于剂量率变化的分析研究中，可以将监测器数据及气象数据视作变量，即电池电压、γ 辐射监测仪高压、温度、湿度、气压、雨量、风向、风速、感雨等。由于来源不同，因此获取的时间无法简单地同步，数据中可能会存在数据范围不统一、数据存在少量缺失值等问题。因此，针对变量单位不统一造成的数值范围不统一，需要依具数据变量的固定单位，对数据的数值范围进行调整。

1. 3. 3 数据去噪

时间序列本身具有非线性和信噪比高的特点，采用传统的高斯去噪、中值滤波等方法往往存在诸多缺陷。由于离散小波变换（DWT）在高频信号降噪方面的应用广泛，因此通常采用离散小波变换，选择紧支撑、具有对称性、与信号波形相似的小波对时序数据进行降噪[7] 。离散小波变换公式如下[8] ：

式中， α 代表比例因子， β 代表定位因子， e（λ） 为连续时间信号并非离散信号。根据设定阈值，保留大于阈值的系数，再进行反向离散小波变换来重建信号，获得降噪后的信号。

1. 3. 4 数据缺失值处理

根据本文实验数据集的特性，对于部分相关性不强以及无关的特征值列，为保证分析的准确性，可以通过删除法将其去除。对于剩余特征值的行缺失数据，若通过删除缺失值的方式对缺失值进行处理，对原始数据的子集进行挖掘，很可能造成分析结果由于基于局部产生偏差。因此，我们主要采用基于填充技术的插补法，避免了删除法的弊端，使得数据集中的重要信息得以保留。为保证插补值的准确性，从缺失数据时间间隔的限制、变量自身特性、变量间的相关性以及与时间序列的关系等不同方面出发，对行缺失数据进行填补。主要变量类型可分为以下三种：

（1）辐射剂量率数据：由于辐射剂量率与其他变量间存在关系，且与时序变动有很强的趋势，因此我们可以优先采用冷卡填充的方法，选择与缺失对象特征最为相似的第一个对象并进行填充，即在所有样本中测量不同特征值之间的欧式距离进行分类，选择与待填充样本在特征空间中的1个最近邻，再对剩余剂量率数据采用线性插值法进行填充。

（2）监测器数据：监测器数据由γ 辐射监测仪高压及电池电压组成。由于监测器数据与其他变量相关性较弱，因此基于电压本身随时间变化的特性，我們根据缺失时间点前后时段相邻最近的数据，采用线性插值法对缺失时间点处的γ 辐射监测仪高压及电池电压进行填充。

（3） 气象数据：气象数据由温度、气压、湿度、雨量、感雨、风向、风速组成。由于变量间相关性较强，且随时间波动，我们采用时序中最基本的就近插补法，替换缺失值为缺失时间点之前或之后最近的观测值，对温度、气压、湿度、雨量、感雨、风向、风速进行填充，再对剩余气象数据采用线性插值法进行填充。

1. 4 数据变换

为了解决可能存在的站点数据采样周期不统一、采样周期过小而导致数据量巨大、采样周期过大而研究过程需要更小采样周期等问题，须依具研究需求将数据变频为高级别或低级别周期，即降采样或增采样。为了控制数据规模，降低模型训练开销，提高运算效率，通常选用降采样的方式。一般情况下降采样有最大值采样、平均值采样和区域采样及随其区域采样等。我们通过对比30 秒频率数据采用平均值求采及最大值求采至5分钟频率数据后辐射剂量率的数据变化曲线，发现若划分5 分钟长度时间窗口进行数据平均会造成单点极大值在临近时间段的平均，降低数据的明显差异，因此，我们需要采用划分5 分钟长度时间窗口进行数据最大值的采样方法以保证检测长时间段内持续的特殊情况。

1. 5 数据转换

由于不同变量的评价指标不同，具有不同的量纲，数据数值间的差别可能很大，为了消除指标之间的量纲和取值范围差异对数据分析结果的影响，需要对数据进行标准化处理，即将数据按照比例缩放，使之落入一个特定的区间，以便于后期对数据的分析及处理。根据算法及模型的选择，通常我们需要在数据预处理中或者模型中选择不同标准化方法对数据进行标准化处理。常用的标准化方法主要有离差标准化，z-score 标准化等。

2 特殊数据检测

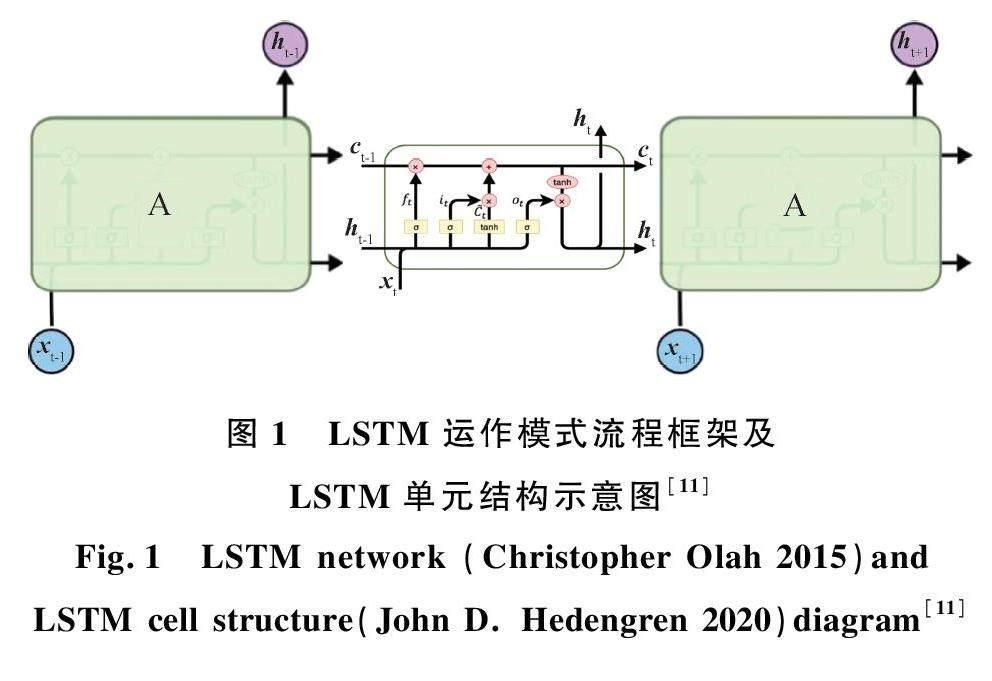
LSTM 是一种特殊的递归神经网络[9] ，由于具有长期学习依赖关系的能力，非常适合预测时间序列数据，也常被用于监测变量集体水平上的特殊数据检测。LSTM 通过对训练集数据进行训练，按照固定时间步长生成预测器，来预测下一时间点的辐射剂量率特征，对预测误差信号的分布概率进行估计，选取阈值，按照预测误差区分正常数据与特殊数据[10] 。

如图1 所示，LSTM 架构由LSTM 单元组成，每个LSTM 单元包含输入节点、输出节点及由许多智能节点组成的隐藏层。A 代表一个完整的LSTM 单元，接受序列当前时间节点的输入向量xt ，输出当前隐藏状态向量ht ， 并传递至下一单元[11] 。

每个LSTM 单元包含三个门，即遗忘门、输入门和输出门。这些门使 LSTM 网络能够不断地重置、写入和读取单元格，可被表示为式（4）：

3 性能评估指标

为了评估特殊数据检测算法的性能，我们以算法检测出来的正确样本为主，平衡正负样本关系，主要评估算法的准确率、精确率和召回率以及F1 分数。TP （True Positive） 表示真正样本数，TN（True Negative ） 表示真负样本数， FP （ FalsePositive）表示假正样本数，FN （False Negative） 表示假负样本数[8] 。

准确率（Accuracy） 是最为常见及直观的评价指标，是全部样本中被预测正确的样本概率，对全部正负样本结果中的预测准确程度，表达式为式（5）：

4 实验结果及评估

4. 1 数据集简介

本文所用到的辐射剂量率及相关监测数据均由监测站点提供，所有站点均布设辐射剂量率连续监测设备及微型气象站，提供γ 辐射剂量率数据及风向、风速、温度、湿度、气压、雨量和感雨等气象数据。数据时间范围为2019 年1 月1 日0 时到2020 年1 月1 日0 时。另外，在特殊数据检测实验中，用到的测试数据来源于A 站带人工标注标签数据，数据时间范围为2019 年1 月1 日0 时到2021 年1 月1 日0 时。

由于监测站点间地理位置差距较大，各监测站点本底剂量率数据存在明显差异，某时段逐时辐射剂量率如图2 所示。因此本论文对不同站点的数据分布状态及数据情况进行了统计分析，表1为其中5 个监测站点辐射剂量率的分布情况，从中可以看出各站辐射剂量率监测数据偏度均大于1. 5，分布不对称、形态偏斜、高峰陡峭，呈偏态分布。其中B 站辐射剂量率统计分布示例如图3所示。

4. 2 数据降噪结果

小波分析库PyWavelets 提供了众多可供选择的小波族， 例如Haar （ haar）、Daubechies （ db）、Symlets （sym）、Coiflets （coif）、Biorthogonal （bior）等。每个小波族下有不同的系数，共127 个小波基函数。其中多贝西小波（Daubechies Wavelet）是最常使用到的小波转换，主要应用在离散型的小波转换，通常使用在信号分析、信号压缩跟噪声去除。为保证通过离散小波变换（DWT）后的去噪结果仍保留原始时序数据的规律性等特性以及特殊数据的突出部分，我们选用db38 的结果进行去噪。图4 展示出A 站某时段进行离散小波变换降噪后的剂量率变化与原始时序数据对比。可以看到，经过降噪后的剂量率变化曲线变得更为平滑，噪声数据减少，可以更加明显地区分正常数据与特殊数据，进而有效地避免了噪声数据对特殊数据检测效果的影响。

4. 3 实验设置

在特殊数据检测模型建模时使用A 站2019—2020 年带人工标注标签数据集（正常数据标签为0，特殊数据标签为1），按照0. 7、0. 15、0. 15 的比例将数据集随机划分为独立的训练集、测试集、验证集。利用训练集与验证集建立模型并优化，通过测试集预测标签结果与实际标签从准确率、精确率、召回率、F1-分数方面进行评估。

LSTM 模型输入数据为Z-score 标准化变换后的数据，输入维度为：（样本数量，时间步长，特征数量），将每个时间点的输入当作该点数据全部特征的集合，即7 维向量，包含剂量率值、气压值、温度值、湿度值、雨量值、风向值、风速值;时间步长设置为1，表示每个时间点的结果由前1 个时间点来进行预测。因此，模型的输入维度为：（样本数量，1，7）。

LSTM 模型激活函数为tanh，循环激活函数为sigmoid。通过RMSprop 优化器进行模型优化。为了让模型可以快速收敛到最优解，且在训练后期更加稳定，采用动态学习率在学习中进行调整。初始学习率设置为0. 1，当评价指标F1-分数在连续10 个epoch 后不再提升时，则减少学习率至原学习率的0. 1 倍， 直到学习率降低到最小值0. 001。

基于A 站预处理后带标签的数据训练模型，通过网格搜索对RMSprop 学习效率等模型参数进行选择。在实验过程中，我们对模型的超参数进行调优，选择隐藏层大小为256，设置batch 尺寸为128，epoch 数量为50。在模型对训练数据进行训练过程中，对每个epoch 通过F1-分数来评估模型在训练集和验证集上的性能，如图5 所示。对训练好的模型通过准确率、精确率、召回率、F1-分数来对模型进行评估。并且进行更精细的调优，例如尝试不同数量的LSTM 隐藏单元等方法，进一步提高模型的检测性能。

4. 4 性能评估

A 站2019 年某时段及该时段部分放大辐射剂量率数据预处理可视化如图6 所示，可以看到，预处理后的数据对缺失数据进行了有效填充，且保留了原频率时序数据波动特征，平滑了剂量率时间序列曲线。

同时，基于A 站2019—2020 年带人工标注标签数据，我们通过对特殊数据算法的评估，研究数据预处理步骤对基于LSTM 特殊数据检测算法性能的影响，实验结果列于表2。该表为LSTM 二分类模型5 次运行结果的平均表现，通过表2 可以得出，原始数据在经过数据清洗、数据变换后，应用LSTM 模型后的准确率、精确率、召回率及F1-分数均存在提升，其中精确率、召回率与F1-分数提升幅度较大， 分别提高了58. 8%、237. 3%、176. 6%。

为了进一步探究数据预处理是否会对特殊数据的预警产生影响，实验将原始数据及预处理后数据分别通过检测模型，对比得到的特殊数据与实际人工标注的特殊数据，并基于时间序列绘制经模型检测出的辐射剂量率特殊数据散点图，如图7 所示。图中，以测试集中人工标注的特殊数据为标准，对模型检测出的特殊数据与人工标注的特殊数据重合点比例进行放大，可以更直观的展示出，经预处理后的数据相较于原数据带入模型后，检测出的正确特殊数据更多，更为精确。我们不失一般性地选取一组不同输入的模型检测结果（即测试集的原数据与预处理数据分别输入模型后检测出的特殊数据），并将它们与测试集中的人工标注特殊数据进行比较，检测出的特殊数据关系如图8 韦恩图所示。在测试集30 711 条数据中，人工标注的特殊数据数量为3 967 条，原数据输入模型后检测出的特殊数据数量为2 338 条，正确检测出特殊数据共1 140 条，精确率为28. 74%，召回率为48. 76%;预处理数据输入模型后检测出的特殊数据数量为4 329 条，正确检测出特殊数据共2 492 条，精确率为62. 82%，召回率为57. 57%，明显优于原数据作为模型输入数据得到的检测结果， 通过评估此组模型不同输入的检测结果，可以看出经预处理后的数据更适合作为检测模型的输入数据，检测效果更好。另外，预处理数据与原数据输入模型后检测出的特殊数据重合率占原数据检测结果的64. 97%，其中88. 51%为正确检测出的特殊数据，表明数据预处理并不会降低预警的灵敏度。因此，我們得出结论，数据预处理可以有效地提高数据质量，且数据预处理并不会对特殊数据的预警产生影响。

5 结论

本文介绍了基于时间序列分析的数据预处理步骤，包括数据统计分析、数据清洗、数据变换及转换处理，并对环境辐射剂量率数据集进行了数据预处理及特殊数据检测实验研究，通过无预处理的原始数据及预处理后的辐射剂量率特殊数据检测结果进行评估，结果表明，经过预处理后的数据应用于LSTM 特殊数据检测模型后，在准确率、精确率、召回率及F1-分数方面都有所提高，这说明应用适当的预处理可以有效提高特殊数据检测结果及数据质量，为后续数据挖掘及特殊数据分析提供有力帮助。在后续研究中，我们可以通过多个方面对数据预处理方法进行优化，其中，对缺失值的处理是影响数据预处理效果的重要部分，我们可以根据经验及多次实验增加更为细化的填充规则，例如，设置更为准确的缺失值填充方法的时间间隔限制，采用不同的机器学习及时间序列预测方法等。