基于无监督学习的编码衍射成像方法研究
石保顺 吴一凡 练秋生


摘 要:
编码衍射成像旨在利用衍射强度图样重建原始图像,而现有基于人工设计先验的编码衍射成像算法大都在低信噪比下成像质量低。通过基于深度神经网络学习的深度先验能够解决上述问题,但有监督学习需要大规模样本对,不利于实际应用。针对这一问题,本文提出一种基于无监督学习的编码衍射成像方法。该方法结合双数据保真项、卷积稀疏编码模型和深度图像先验模型构建了能够融合互补先验的优化模型,并利用交替优化方法对其进行有效求解。实验结果表明,提出的方法能够在低信噪比下仅通过单幅编码衍射强度图样重建出高质量的图像。
关键词:
计算成像;衍射成像;无监督学习;深度图像先验;卷积稀疏编码
中图分类号: TP391.41, O436 文献标识码: A DOI:10.3969/j.issn.1007-791X.2023.01.006
0 引言
编码衍射成像作为相位恢复领域的一个研究热点,在生物学[1]、医学[2]、光学[3-4]及天文学[5]领域有着广泛应用。编码衍射成像系统在观测物体后加入随机相位板对物体结构信息进行调制,通过探测器记录编码衍射图样(Coded diffraction patterns, CDP)。由于采样设备的限制,探测器只能记录衍射图样的强度值,导致测量的数据丢失了相位信息。因此通过CDP重建原始图像是一个高度不适定的非凸、非线性问题,如何对该问题进行有效求解是一大挑战。
解决该非凸优化问题的一个思路是通过数学方法构建较好的初始解并利用基于梯度的迭代算法进行求解,主要代表算法有WF (Wirtinger flow)算法[6]、TWF (Truncated wirtinger flow)算法[7]、TAF (Truncated amplitude flow)算法[8]等。该类方法未利用先验信息,导致重建高质量图像需要多幅编码衍射图样。为解决该问题,基于人工设计先验的算法利用图像固有先验信息进行编码衍射成像,例如基于稀疏性的衍射成像算法[9-13]及基于非局部相似性的衍射成像算法[14-17]等。Tillmann等[9]利用图像在自适应字典下的稀疏性,提出了DOLPHIn算法用于编码衍射成像。Chang等[10]通过构造全变差正则项引入梯度稀疏性来提高相位恢复的重建质量。Shi等[11]提出了一种正则化与交替投影框架相结合的编码衍射成像算法,有效地将BM3D (Block matching and 3D collaborative filtering)框架下的稀疏性引入到圖像重建中。Katkovnik等基于物体相位和振幅在变换域的稀疏性,结合GS (Gerchberg-Saxton)[18]算法提出了能够进行像素分辨率衍射成像的SPAR (Sparse phase amplitude reconstruction)[14]算法及亚像素分辨率衍射成像的SR-SPAR (Super-resolution sparse phase amplitude retrieval)[15]算法。上述基于人工设计先验的编码衍射成像算法利用的先验是通过解析方法刻画的,难以充分描述所有图像的统计分布信息。因此,利用人工设计先验的编码衍射成像算法的重建质量有很大提升空间。
近些年,深度学习技术引起了学者们的广泛关注,该技术能够利用大规模数据集和深度神经网络强大的表示能力学习对训练数据集最优的网络模型[19-20]。Hand等[21]提出了一种基于生成先验的相位恢复框架,证明了在相位恢复任务中利用生成模型的策略优于基于稀疏性的相位恢复算法。针对相位恢复问题,Morales等[22]提出了一种端到端的方法,该方法通过联合学习谱初始化和深度神经网络参数来解决相位恢复问题。上述基于有监督学习方法训练的深度神经网络对特定信噪比是最优的,但对其他信噪比是非最优的。因而,在不同信噪比下,上述方法需要重新训练深度神经网络,灵活性较差。为弥补该不足,即插即用方法将事先训练好的深度高斯去噪器引入到优化过程中。其中Metzler等[23]将卷积神经网络去噪器引入到去噪正则化(Regularization by denoising, RED)[24]框架提出了prDeep算法,Shi等[25]利用图像与去噪图像的相似性提出了能够融合深度去噪器先验的稀疏表示正则化模型,有效提高了编码衍射成像的成像质量及分辨率。
上述编码衍射成像网络或深度高斯去噪器都采用有监督的学习方式进行学习,泛化能力较差,并且深度神经网络训练需要大规模数据集。为解决该问题,Ulyanov等[26]提出一种称为深度图像先验(Deep image prior, DIP)的无监督深度学习框架。图像的统计分布可以由深度神经网络结构本身所表征,基于该观测,DIP能够仅通过退化图像学习网络参数并表征图像。DIP的提出为深度学习提供了一种新的思路,即无监督学习,其参数并不需要通过大量的外部数据集进行学习。然而,DIP框架存在过拟合的问题,解决该问题最直接的方式是早停技术,但最优的早停迭代次数难以精确获得。为弥补该不足,Cheng等[27]提出了基于随机梯度Langevin动力学进行后验推断的DIP,该方法不需要早停技术就能够获得满意解。为进一步提升DIP求解图像反问题的性能,学者们将传统先验与DIP相结合以提升重建质量,例如Sun等[28]将即插即用先验与DIP相结合,解决了由过拟合导致的DIP算法重建质量低的问题。Cascarano等[29]将梯度稀疏性与DIP相结合进行了高质量的图像复原。Mataev等[30]通过引入RED模型,将非局部相似性与DIP相结合提出了DeepRED算法,该算法较原始RED和DIP算法的性能具有显著提升。
上述无监督学习方法针对线性、凸问题取得了较好的效果,但当采用无监督学习方法求解编码衍射成像等非线性、非凸优化问题时,仍存在以下挑战:1)现有基于深度图像先验的方法并未充分利用图像固有先验信息,如何挖掘并利用互补的图像先验信息提升重建质量是一大挑战;2) DeepRED算法能够利用互补先验知识进行图像重建,但估计图像过程中并未充分挖掘测量数据包含的待重建图像信息。为解决这两个问题,受卷积稀疏编码(Convolutional sparse coding, CSC)[31-32]及双数据保真项在单曝光压缩成像[33]领域成功应用的启发,本文通过双数据保真项、卷积稀疏编码模型和深度图像先验模型提出一种基于无监督学习的编码衍射成像算法。在本文提出的方法中,CSC模型通过线下训练好的卷积字典表示图像,DIP通过退化图像优化深度神经网络的参数,实现深度神经网络的“线上”训练。两者有效结合,理论上能够有效融合互补先验知识。双数据保真项有利于进一步挖掘编码衍射强度图样中的信息,辅助DIP框架中参数的无监督学习。因此,与现有编码衍射成像算法相比,本文提出的算法有望在低信噪比情况下仅通过单幅编码衍射图样重建更高质量的图像。
3 分析与讨论
3.1 实验细节与参数设置
测试图像如图1所示。其中前6幅是prDeep算法软件包(https://github.com/ricedsp/prDeep)中大小为512×512的标准化灰度图像。后14幅图像来源于细胞图像库(The Cell Image Library: http://www.cellimagelibrary.org/home),每幅原始细胞图像被裁剪为512×512的标准化灰度图像。
算法的参数通过经验调整设置,具体地,实验过程中将外循环设置为i=40次,每次循环中DIP内循环设置为2i次。使用ADAM作为优化器,学习率初始值设置为0.001。投影次数J在信噪比(Signal-to-noise ratio, SNR)为5 dB,10 dB和15 dB三种情况下分别设为2,2和4。DCD-DIP算法其他参数设置如表1所示。本文通过小波域估计算法[42]对噪声标准差进行估计,并采用与文献[11]输入噪声标准差相同的的计算方式,即输入标准差为估计标准差乘以常数Q。
所有算法都在同一个四元随机掩模条件下进行实验与比较。所有实验均采用随机初始值,随机种子固定。本文采用峰值信噪比(Peak signal to noise ratio, PSNR)和結构相似性(Structure similarity index measure, SSIM)作为评价算法重建性能的客观指标,PSNR值越高,说明图像重建质量越高;SSIM值越高,说明两幅图像的相似程度越高。所有实验均在Intel Core i9-10850k@3.60 GHz、内存64 GB、NVIDIA GTX 3080Ti GPU的硬件平台上进行。
3.2 双数据保真项对重建结果影响分析
为分析双数据保真项的有效性,本节将仅利用DIP框架的成像算法、单数据保真项的成像算法及本文提出的采用双数据保真项的DCD-DIP算法进行编码衍射成像实验,并对实验结果进行对比。对于单数据保真项的成像算法,去除式(8)中的第一项,ρ设为1并将其他参数调制最优,其参数如表2所示。图2中给出了在不同信噪比下三种算法重建测试图像平均PSNR值和SSIM值的比较。从图中可以看出,本文所提出的采用双数据保真项的DCD-DIP算法在重建质量及结构相似性上明显优于另两种算法,说明其能够充分利用互补先验知识,挖掘测量数据包含的图像信息进行图像重建。
3.3 低信噪比下多种编码衍射成像算法的比较及分析
为验证本文算法在低信噪比下的有效性,本节在不同信噪比下与现有编码衍射成像方法进行对比。在信噪比分别为5 dB、10 dB和15 dB时,将本文提出DCD-DIP算法与DOLPHIn[9]、BM3D-prGAMP[17]、SPAR[14]和prDeep[23]算法重建图像的性能进行比较。表3给出了20幅测试图像在不同信噪比下利用上述五种算法进行图像重建的平均PSNR值和SSIM值。由表3可知,本文所提出算法在不同信噪比下的PSNR值和SSIM值均明显高于对比算法。DOLPHIn算法在CDP数量较少以及低信噪比的情况下重建性能较差。BM3D-prGAMP和SPAR算法利用图像的非局部相似性及相似块的稀疏性,能够获得比DOLPHIn算法高的重建质量。prDeep算法通过有监督训练的去噪器利用深度先验进行重建,其重建质量优于基于BM3D的成像算法,但在信噪比较低情况下重建质量仍然较差。而本文提出的算法通过融合互补的先验知识,采用双数据保真项充分挖掘单幅编码衍射强度图样中的信息,较上述四种对比算法的性能具有显著的提升。
为进一步说明算法的有效性,图3~5展示了信噪比分别为5 dB,10 dB,15 dB时,不同算法重建Pollen、Alcea Rosea、Butterfly图像的视觉效果及部分放大效果图。由重建图像及放大部分可以看出,DOLPHIn算法的重建图像中存在着明显的块效应;BM3D-prGAMP算法的重建图像缺失了大量细节且存在伪影;SPAR算法重建图像细节较好,但伪影较为明显;prDeep算法重建图像较为平滑,导致大量的细节丢失。本文提出的DCD-DIP算法重建图像视觉效果较好,保留了大量细节信息,有效消除了块效应和伪影。综上所述,DCD-DIP算法在不同信噪比下均表现出了良好的性能。
3.4 收敛性分析
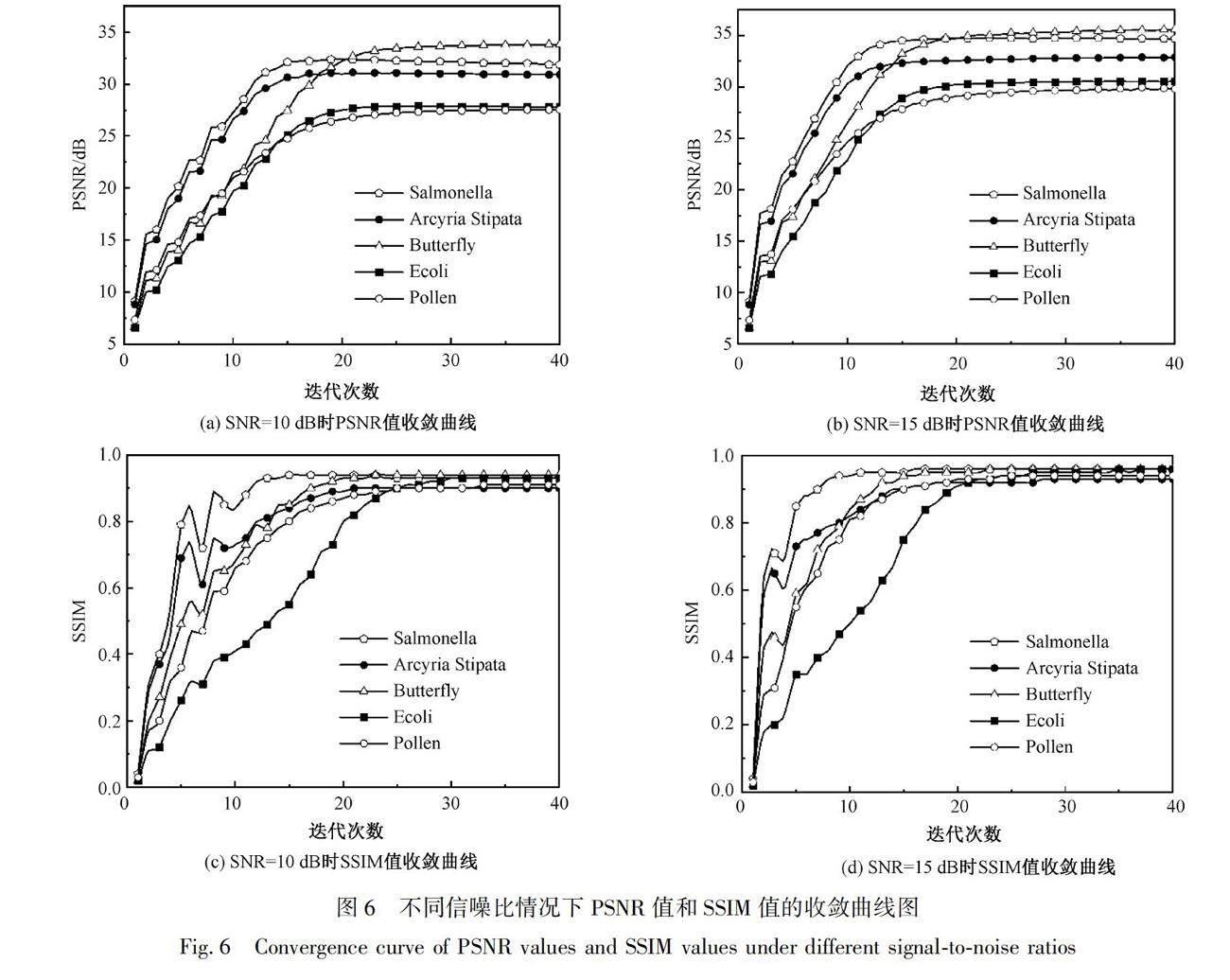
提出的DCD-DIP算法求解的是一个非凸优化问题,虽然能够取得较好的重建效果,但很难从理论上严格证明其收敛性。为说明该算法具有良好的收敛性能,图6给出了在信噪比10 dB和15 dB情况下获得的PSNR值和SSIM值随迭代次数变化的曲线图。从图6中看出PSNR值和SSIM值随着迭代次数的增加呈不断上升直至平稳的趋势,SNR=10 dB时经25次迭代PSNR值和SSIM值趋近于平稳,SNR=15 dB时迭代到20次时趋近于平稳。由此可以说明DCD-DIP算法具有良好的收敛性能。此外,从图中可以看出,SSIM值在第1次到第10次迭代过程中存在波动。由于求解优化问题本身的非凸性,收敛曲线存在波动是合理的。
4 结论
本文将深度卷积稀疏编码与深度图像先验模型相结合,利用双数据保真项提出了一种面向编码衍射成像的无监督学习算法。该算法无需样本标签及大规模数据集,仅通过单次观测的编码衍射强度图样就能够同时实现低信噪比下的高质量图像重建及深度神经网络参数的优化。提出的算法能够融合互补先验知识,实验结果表明该算法重建质量优于现有编码衍射成像算法。
参考文献
[1] WU J, LU Z, JIANG D, et al. Iterative tomography with digital adaptive optics permits hour-long intravital observation of 3D subcellular dynamics at millisecond scale[J]. Cell, 2021, 184(12): 3318-3332.
[2] AKCAKAYA M, TAROKH V. Sparse signal recovery from a mixture of linear and magnitude-only measurements[J]. IEEE Signal Processing Letters, 2015, 22(9): 1220-1223.
[3] MILLANE R P. Phase retrieval in crystallography and optics[J]. Journal of the Optical Society of America A, 1990, 7(3): 394-411.
[4] SHECHTMAN Y, ELDAR Y C, COHEN O, et al. Phase retrieval with application to optical imaging: a contemporary overview[J]. IEEE Signal Processing Magazine, 2015, 32(3): 87-109.
[5] JAGANATHAN K, OYMAK S, HASSIBI B. Sparse phase retrieval: uniqueness guarantees and recovery algorithms[J]. IEEE Transactions on Signal Processing, 2017, 65(9): 2402-2410.
[6] CANDS E J, LI X D, SOLTANOLKOTABI M. Phase retrieval via wirtinger flow: theory and algorithms[J]. IEEE Transactions on Information Theory, 2015, 61(4): 1985-2007.
[7] CHEN Y X, CANDS E J. Solving random quadratic systems of equations is nearly as easy as solving linear systems[J]. Communications on Pure and Applied Mathematics, 2017, 70(5): 822-883.
[8] WANG G, GIANNAKIS G B, ELDAR C Y. Solving systems of random quadratic equations via truncated amplitude flow[J]. IEEE Transactions on Information Theory, 2018, 64(2): 773-794.
[9] TILLMANN A M, ELDAR Y C, MAIRAL J. DOLPHIn—Dictionary learning for phase retrieval[J]. IEEE Transactions on Signal Processing, 2016, 64(24): 6485-6500.
[10] CHANG H B, LOU Y F, NG M K, et al. Phase retrieval from incomplete magnitude information via total variation regularization[J]. SIAM Journal on Scientific Computing, 2016, 38(6): A3672-A3695.
[11] SHI B S, LIAN Q S, HUANG X, et al. Constrained phase retrieval: when alternating projection meets regularization[J]. Journal of the Optical Society of America B, 2018, 35(6): 1271-1281.
[12] CHANG H B, MARCHESINI S. Denoising poisson phaseless measurements via orthogonal dictionary learning[J]. Optics Express, 2018, 26(16): 19773-19796.
[13] 練秋生, 李颖,陈书贞. 融合多种小波与全变差正则化的相位恢复算法[J]. 光学学报, 2018, 38(2): 298-305.
LIAN Q S, LI Y, CHEN S Z. Phase retrieval algorithm fusing multiple wavelets and total variation regularization[J]. Acta Optica Sinica, 2018, 38(2): 298-305.
[14] KATKOVNIK V, EGIAZARIAN K. Sparse superresolution phase retrieval from phase-coded noisy intensity patterns[J]. Optical Engineering, 2017, 56(9): 094103.
[15] KATKOVNIK V, SHEVKUNOV I, PETROV N V, et al. Computational super-resolution phase retrieval from multiple phase-coded diffraction patterns: simulation study and experiments[J]. Optica, 2017, 4(7): 786-794.
[16] KOCSIS P, SHEVKUNOV I, KATKOVNIK V, et al. Single-shot pixel super-resolution phase imaging by wavefront separation approach[J]. Optics Express, 2021, 29(26): 43662-43678.
[17] METZLER C A, MALEKI A, BARANIUK R G. BM3D-PRGAMP: Compressive phase retrieval based on BM3D denoising[C]//Proceedings of the IEEE International Conference on Image Processing, Phoenix, AZ, USA, 2016: 2504-2508.
[18] GERCHBERG R W, SAXTON W. A practical algorithm for the determination of phase from image and diffraction plane pictures[J]. Optik, 1972, 35(2): 237-246.
[19] 姜萬录, 李振宝,雷亚飞,等.基于深度学习的滚动轴承故障诊断与性能退化程度识别方法[J].燕山大学学报,2020,44(6):526-536
JIANG W L,LI Z B,LEI Y F, et al.Deep learning based rolling bearing fault diagnosis and performance degradation degree recognition method[J].Journal of Yanshan University,2020,44(6):526-536.
[20] 李林祥,袁毅,温淑焕.基于BAU-Net的高分辨率遥感图像中建筑物的分割提取 [J].燕山大学学报,2021,45(4):335-342.
LI L X,YUAN Y,WEN S H.BAU-Net for buildings segmentation in high resolution remote sensing images[J].Journal of Yanshan University,2021,45(4):335-342.
[21] HAND P, LEONG O, VORONINSKI V. Phase retrieval under a generative prior[C]//Proceedings of the International Conference on Neural Information Processing Systems, Montréal,Canada, 2018: 9154-9164.
[22] MORALES D, JEREZ A, ARGUELLO H. Learning spectral initialization for phase retrieval via deep neural networks[J]. Applied Optics, 2022, 61(9): F25-F33.
[23] METZLER C A, SCHNITER P, VEERARAGHAVAN A, et al. prDeep: Robust phase retrieval with a flexible deep network[C]//Proceedings of International Conference on Machine Learning, Stockholm, Sweden, 2018, 80: 3501-3510.
[24] ROMANO Y, ELAD M, MILANFAR P. The little engine that could: regularization by denoising (RED)[J]. SIAM Journal on Imaging Sciences, 2017, 10(4): 1804-1844.
[25] SHI B S, LIAN Q S, CHANG H B. Deep prior-based sparse representation model for diffraction imaging: a plug-and-play method[J]. Signal Processing, 2020,168:107350.
[26] LEMPITSKY V, VEDALDI A, ULYANOV D. Deep image prior[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 2018: 9446-9454.
[27] CHENG Z Z, GADELHA M, MAJI S, et al. A Bayesian perspective on the deep image prior[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 2019: 5438-5446.
[28] SUN Z D, LATORRE F, SANCHEZ T, et al. A plug-and-play deep image prior[C]//Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Toronto, ON, Canada, 2021:8103-8107.
[29] CASCARANO P, SEBASTIANI A, COLOMBA C M, et al. Combining weighted total variation and deep image prior for natural and medical image restoration via ADMM[C]//Proceedings of theInternational Conference on Computational Science and Its Applications, Cagliari, Italy, 2021: 39-46.
[30] MATAEV G, ELAD M, MILANFAR P. DeepRED: Deep image prior powered by RED[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 2019.
[31] GARCIA-CARDONA C,WOHLBERG B. Convolutional dictionary learning: a comparative review and new algorithms[J]. IEEE Transactions on Computational Imaging, 2018, 4(3): 366-381.
[32] 熊嬌娇,卢红阳,张明辉,等. 基于梯度域的卷积稀疏编码磁共振成像重建[J]. 自动化学报, 2017, 43(10): 1841-1849.
XIONG J J, LU H Y, ZHANG M H, et al. Convolutional sparse coding in gradient domain for MRI reconstruction[J]. Acta Automatica Sinica, 2017, 43(10): 1841-1849.
[33] MENG Z Y, YU Z M, XU K, et al. Self-supervised neural networks for spectral snapshot compressive imaging[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 2021: 2622-2631.
[34] LIU J M, SUN Y, XU X J, et al. Image restoration using total variation regularized deep image prior[C]//Proceedings of International Conference on Acoustics, Speech and Signal Processing, Brighton, UK, 2019:7715-7719.
[35] KINGMA D, BA J. Adam: a method for stochastic optimization[C]//Proceedings of International Conference on Learning Representations, San Diego, USA,2015.
[36] TOFIGHI M, KOSE K, CETIN A E. Denoising using projections onto the epigraph set of convex cost functions[C]//Proceedings of the IEEE International Conference on Image Processing, Paris, France, 2014: 2709-2713.
[37] ZHANG J, ZHAO C, ZHAO D B. Image compressive sensing recovery using adaptively learned sparsifying basis via L0 minimization[J]. Signal Processing, 2014, 103: 114-126.
[38] BRISTOW H, ERIKSSON A, SIMON L. Fast convolutional sparse coding[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 2013: 391-398.
[39] WOHLBERG B. Efficient convolutional sparse coding[C]//Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 2014: 7173-7177.
[40] FU X Y, ZHA J Z, WU F, et al. Jpeg artifacts reduction via deep convolutional sparse coding[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 2019: 2501-2510.
[41] ZHENG H Y, YONG H W, ZHANG L. Deep convolutional dictionary learning for image denoising[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 2021: 630-641.
[42] DING F, CAO T J. Application of daubechies wavelet transform in the estimation of standard deviation of white noise[C]//Proceedings of the Second International Conference on Digital Manufacturing & Automation, Zhangjiajie, China, 2011: 212-215.
Research on coded diffraction imaging method based on unsupervised learning
SHI Baoshun1,2, WU Yifan1,2, LIAN Qiusheng1,2
(1. School of Information Science and Engineering,Yanshan University,Qinhuangdao,Hebei 066004,China;
2. Hebei Key Laboratory of Information Transmission and Signal Processing,Yanshan University,Qinhuangdao,Hebei 066004,China)
Abstract:
Coded diffraction imaging aims to reconstruct the original image by utilizing the intensity of diffraction patterns. However,in the case of low signal-to-noise ratios,most of the existing coded diffraction imaging algorithms based on hand-crafted priors usually suffer from low-quality reconstructions.
The aforementioned problem can be solved by using the deep priors based on deep neural network learning.However, supervised learning methods need massive sample pairs, which is impractical for applications. To address this issue, a coded diffraction imaging method based on the unsupervised learning is proposed in this paper. An optimization model which can fuse complementary priors is formulated by combining the double data fidelity terms, convolutional sparse coding, and deep image prior models.Meanwhile,the alternating optimization method is utilized to solve the optimization model effectively. Experimental results show that the proposed method can reconstruct high-quality images only from single intensity of coded diffraction pattern at low signal-to-noise ratios.
Keywords:
computational imaging;diffraction imaging;unsupervised learning;deep image prior;convolutional sparse coding

