高中数学函数内容单元复习课教学建议

梁慧敏　孙天娇　张涛　李春兰

【摘 要】数学单元复习课在高中数学教学中发挥着至关重要的作用，它是继新知识学习后，对知识的进一步升华与凝练，是对新知识熟能生巧的过程。“题海战术”式的数学单元复习课不符合当前“双减”背景下的教学要求。张奠宙先生曾多次在其文章中强调上好数学复习课的必要性，本文结合张奠宙先生关于数学单元复习课的教育思想，以人教版高中数学（A版）必修第一册第三章“函数的概念与性质”的单元复习课为例，给出数学单元复习课的六条教学建议。

【关键词】张奠宙；单元复习课；函数；数学教育思想

一、引言

2021年7月国家正式颁布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》，其中提出“大力提升教育教学质量，确保学生在校内学足学好”，那么减轻学生负担的根本在于提高学校教育教学的质量。在高中数学课堂中，单元复习课一直以来都对提升教育教学质量起着至关重要的作用。追溯历史的脚步，我国伟大的教育家孔子早在几千年前就强调了复习的重要性——“温故而知新，可以为师矣”。在实际教学中，许多一线教师往往把数学单元复习课看作是简单的习题课来讲授，以高强度、大容量的解题训练为主。显然，“题海战术”式的复习课已经不能适应当前“双减”背景下的教学要求。数学单元复习课不是简单地回顾前面所学的知识，而是通过复习达到融会贯通、举一反三、温故知新的效果，并促进学生数学核心素养的培养，以适应当前“双减”背景的教学要求。

早在2010年，张奠宙先生等就指出当时复习课中存在的许多弊端，如“公开课中难见好的复习课，大多是大容量、快节奏、高密度的解题训练课”。［1］叶立军等指出复习课不是简单的炒冷饭，而是对学生认识的继续、深化和提高。［2］杨汉鑫也指出了现在高中数学复习课中存在的一些问题，如教师缺乏“科学方法”，在复习课上只是简单分析知识点，然后以大量习题训练为主等。［3］单元复习课不能单纯地变成高强度的解题训练课，不能只是简单的分析而缺乏对知识的整体梳理，更不能忽视学生的自主思考及思维能力的培养。要想更好地改进单元复习课，就要找到根源问题，对症下药。

二、数学单元复习课及其作用

（一）数学单元复习课

单元复习课与新授课、习题课等课型在教学目标、教学方式等方面均有较大的不同。数学单元复习课是指根据学生的认知特点和规律，在一个单元教学之后，对所学知识进行系统复习整理的课型。单元复习课的目的是巩固、梳理已学知识、技能，通过对知识的复习整理，帮助学生对所学知识形成结构化认知，提炼数学知识的思想方法，达到对知识的融会贯通。

张奠宙先生等指出，数学知识的认识过程包含“前半段”和“后半段”。［4］单元复习课即“后半段”的学习，应重视反思、辨析、欣赏、提炼数学思想方法等。故教师在进行数学单元复习课教学时要做到：塑造学生的系统知识结构；促进学生形成理性批判、反思等思维；培养学生的探索发现精神；用数学美的内在力量影响学生，体现数学科学的教育性。

依据信息加工心理学，学生的学习是信息加工的过程，主要包括注意过程、短时记忆、编码、长时记忆及信息的提取等五个部分。其中，信息提取的过程是记忆内容梳理、重建的过程，而不是简单的复述。针对学生在学习的过程中不可避免的遗忘现象，信息加工“激活理论”认为，信息要先被激活，才能提取。而信息不能被激活的情况有三种［5］：第一，学生对知识间的联系掌握得不紧密；第二，对信息加工的深度不够；第三，缺乏对知识的联想而不能提取信息。

由信息加工理论出发，可以总结出，在新知识的学习过程中，知识的习得与记忆主要在新授课中进行，而知识的信息提取亦不可或缺，此时就需要单元复习课充分发挥其功能与价值。首先，在单元复习课中应构建整体知识结构体系，以加强知识间的联系。其次，通过融入数学思想方法，加深学生对知识的理解深度，促进信息加工。最后，采用多种数学表征形式，以多种表征的方式提升学生对知识的联想能力，促进学生的信息加工。复习课不是简单的炒冷饭，不能生硬地把数学知识直接传授给学生，而应在其中添加数学美、数学思想方法等数学的“调味剂”。

（二）数学单元复习课的作用

随着新课改的不斷推进与完善，形成了以核心素养为导向的教学目标，反映了新时期对人才培养的要求。对教师而言，上好一节数学单元复习课需要重视数学知识的整体性、系统性以及知识之间的关联性，并合理地规划和安排数学单元复习课。例如，在高中函数概念的复习课中，再次强调函数概念是由初中“变量说”到现在的“集合—对应说”，帮助学生建立关于函数概念的整体知识体系。建立这样的整体知识体系不仅有利于提高课堂效率，培养教师的教学技能，提升教师的专业素养，而且通过不断优化数学单元复习课教学还可以达到促进教师自我发展的目的。此外，在数学单元复习课教学中，教师可以及时发现学生的知识盲点与困惑，掌握学生的学习情况，针对学生掌握不到位的知识进行着重讲解。

对学生而言，数学单元复习课可以帮助学生更加全面地掌握数学单元知识点，建立知识间的联系，由点及面，横向、纵向地深入拓展，从而对知识有更加深入的了解。此外，在单元复习课上采用总结单元典型例题的方法，而不是采用“题海战术”的方式，能够更加有效地提高课堂教学质量，减轻学生的学习负担，并且通过学习相应的数学思想方法，还可以提升学生的数学核心素养。

三、数学单元复习课教学建议

张奠宙先生针对复习课存在的问题，提出了好的数学单元复习课应涉及以下六个方面：一是整体知识框架；二是使用数学思想方法；三是数学本质；四是各种数学表征；五是美学欣赏；六是人文背景。［6］基于此，本文以“函数的概念与性质”这一单元复习课为例，给出数学单元复习课的教学建议。通过对高中函数的概念与性质的复习，学生能经历完整的函数概念抽象过程，掌握其中蕴含的数学思想和方法，形成良好的问题解决能力、思考问题的习惯等。

（一）构建整体知识框架

复习课的重点是帮助学生总结知识并做进一步的巩固提升，所以构建数学单元整体知识框架是数学单元复习课中必不可少的环节。通过构建整体知识框架可以呈现单元知识间的内在联系，加强学生对本单元内容的整体认识，形成清晰的思维脉络。

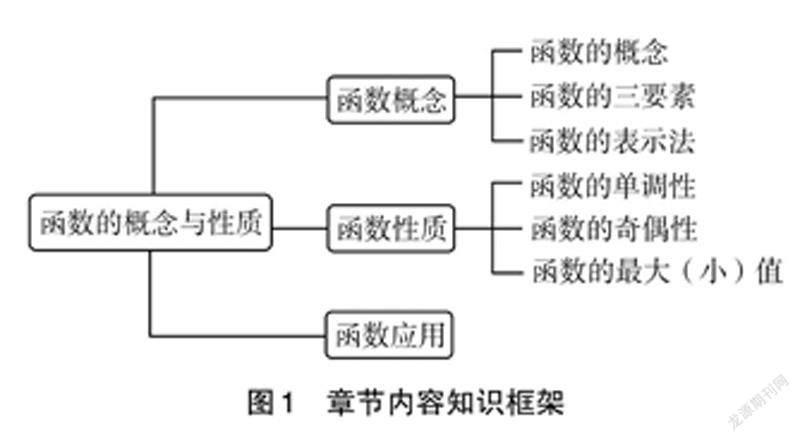
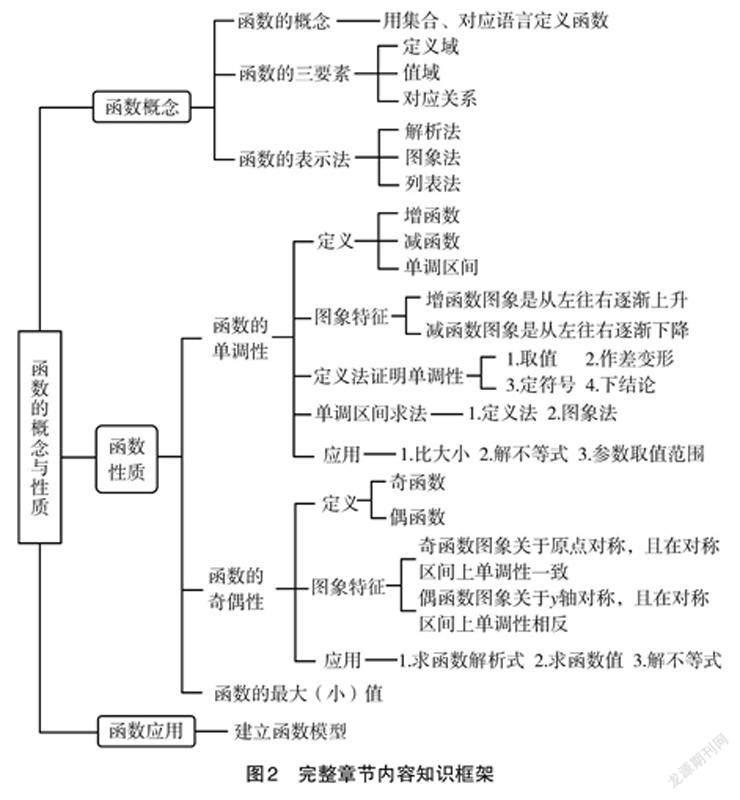
例如，在高中“函数的概念与性质”这一单元复习课上，课堂伊始，教师展示一部分本章内容知识框架（如图1），让学生独立思考将框架填充完整。在补充框架的过程中，若学生遇到困难，教师带领学生一起补充完整（如图2）。

通过思维导图的方式构建函数单元教学的整体知识结构框架，并让学生先自己思考知识点，再由教师引导给出，有助于学生从整体上把握本单元知识体系，加深学生对知识点的理解。

（二）使用数学思想方法

单元知识结构体系如“骨架”，而其中蕴含的数学思想方法如填充其间的“血肉”。因此仅掌握了知识结构体系是不够的，还应掌握其中的数学思想方法。张奠宙先生等提出：“复习课的首要目的是提炼数学思想方法，启示如何熟能生巧，上升到新的境界。”［1］章建跃也指出，通常将数学思想方法从数学思想和数学方法两个角度分别去阐释。［7］其中，数学思想是对数学对象的本质认识，对数学活动具有指导意义；数学方法是指进行数学活动的具体操作方法。数学思想方法是发现和提出数学问题的源泉，是分析和解决数学问题的根本。

在高中“函数的概念与性质”这一单元复习课上，需要向学生渗透的数学思想方法有：函数与方程、数形结合、特殊与一般、分类与整合等。在复习课上学生通过探究典型问题逐步体会数学的思想方法，有助于培养学生用数学的思维思考问题的意识（见表1）。

在单元复习课中，解题训练是必不可少的，但是不能将单元复习课变成大容量、高强度的解题训练课，而应提炼题中蕴含的数学思想方法，帮助学生进行总结归纳，培养学生的解题思维能力及解决问题的能力，有助于学生在后面的学习中学会一题多解、举一反三。

（三）挖掘数学本质

德国数学家克莱因曾将函数称为数学的“灵魂”，并认为函数应该成为中学数学的“基石”。［8］清代数学家李善兰对函数的解释为“凡此变数函彼变数，则此为彼之函数”［9］，确切地反映了函数的本质。随着数学的发展，函数的定义经历了变量说、对应说、关系说［10］的逐步抽象过程。《普通高中数学课程标准（2017年版2020年修订）》对函数概念的教学提倡在初中用变量之间的依赖关系描述函数的基础上，用集合语言和对应关系刻画函数，建立完整的函数概念。［11］19这说明课程标准对初高中函数内容的衔接以及函数本质的教学关注度越来越高。

基于函数教学内容主线，函数单元复习课教学既要“瞻前”，又要“顾后”。回顾小学、立足初中、呼应高中，寻根究底、深入分析，挖掘函数概念的本质。通过展示不同学习阶段函数的概念、内容、应用等方面的内容（如表2），可以让学生在纵向上了解并掌握函数，建立新旧知识之间的联系，寻找知识的固着点，从而更好地理解和掌握函数概念。

“贤者以其昭昭，使人昭昭。”（《孟子》）在教学方面强调教师要想让学生明白所学内容，首先自己要弄明白这些内容。教师应熟练掌握所教内容的本质，才能更好地让学生掌握所学内容的本质，正所谓“要给学生一杯水，教师要有一桶水”。教学的目的不仅是要教会学生如何解题，更重要的是要引导学生去挖掘数学知识的本质及内涵，从根本上理解并掌握数学知识。因此，在数学复习课上就需要教师追本溯源、深入剖析，以高观点的视角进行教学，引导学生思考所学知识的本源。

（四）使用各种数学表征

数学表征是指用某种外显的形式来表达抽象数学知识的过程。［12］著名的认知心理学家西蒙曾指出，表征是问题解决的一个中心环节，它说明问题在头脑中是如何表现出来的。［13］在数学学习以及问题解决的过程中采用多种数学表征方式，有助于拓展学生思维，达到一题多解、融会贯通的效果。此外，对于同一知识，帮助学生在不同的年龄阶段构造不同数学表征方式，将更适合学生学习。

例如，对于函数y=3x+5的教学，美国著名心理学家布鲁纳针对不同学段的学生采用不同的数学表征方式进行教学，对于低学段的学生可以采用□=3△+5这样的图形表征方式，而对于高学段的学生可以使用更为抽象的表征方式y=f （x）。［14］

再如，在高中“函數的概念与性质”单元复习课上，对于函数单调性的描述，可以采用图象语言、文字语言和符号语言等三种表征方式，以达到更好地回顾与掌握函数的单调性概念的目的。通过在复习课上引导学生采用不同的表征方式表达函数单调性，可以有效开拓学生的思维，使其在解决数学问题时不局限于某种表征方式，避免思维定式；同时发展学生的抽象能力与直观想象能力，借助图象探究函数的基本性质，选择合适的数学模型表述变化规律和解决问题。

（五）美学欣赏

罗素曾说：“数学不仅拥有真理，而且还拥有至高的美。”张文俊指出，数学美本质上是自然美的抽象化，既有结论之美，也有方法之美，还有结构之美。［15］在数学单元复习课中向学生展现数学美，有助于学生感受数学的美学价值，使已有知识的基础得到进一步的升华，活跃复习课课堂的氛围。

例如“函数的概念与性质”这一单元中就蕴含着许多数学美。首先，函数的性质之一——函数的奇偶性，图象中就包含着对称美，即奇函数图象关于原点对称，偶函数图象关于y轴对称。其次，高中函数概念是在初中基础上的进一步抽象，用y=f （x）来表示函数，体现了数学中的简洁美。

在数学单元复习课上展现数学美，有助于学生体会数学是富有生命的、美丽的、实用的学科，促使学生喜欢它、热爱它，主动学习数学。

（六）融入人文背景

《普通高中数学课程标准（2017年版2020年修订）》中提出，要将数学文化融入课程内容。数学文化包括数学的思想、精神、语言、方法、观点，以及它们的形成和发展；还包括数学在人类生活、科学技术、社会发展中的贡献和意义，以及与数学相关的人文活动。［11］10

数学单元复习课不仅仅是简单地总结本单元所学知识以及进行大量的习题练习，还应该在数学课本知识的基础上进行进一步的升华。适当地融入相关人文背景，有助于学生更好地理解和掌握单元内容，提高学生学习的兴趣和积极性，并且为学生未来的进一步学习打下堅实的人文背景基础。高中数学单元复习课大致可以从数学游戏、生活实例、数学的发展历程等方面融入相关人文背景。

在“函数的概念与性质”数学单元复习课中，可以从生活实例和数学的发展历程两个方面来融入人文背景。首先，如文中表1内的问题1和问题4是贴近学生生活的函数问题，在复习课中设置这样的问题十分贴切、自然，让学生感受到函数在实际生活中的应用，加深学生对函数的理解，让学生不仅学会函数还学会用函数。其次，“函数的概念与性质”这一章中增设了“函数概念的发展历程”的阅读材料模块，强调在进行了函数内容新授课之后，要在复习课中让学生了解函数概念的人文背景及发展历程。此外，该章的章末还设置了“函数的形成与发展”的文献阅读与数学写作的选学内容。在复习课中布置文献阅读与写作任务，让学生自己查找并补充函数概念发展历程的相关资料，进而完成论文的写作任务，不仅能够扩展学生的知识面，不拘泥于课堂上的内容，而且还有利于因材施教，培养部分学有余力的学生的科研与创新能力，贯彻张奠宙先生等人强调的“数学英才教育”的教学理念。

四、结语

单元复习课是引导学生对单元知识进行梳理、探究、欣赏、升华与凝练的重要课型。要想上好复习课，解题训练不可或缺，但是不能将之作为唯一的教学模式而自我封闭起来，应在回顾本单元知识的基础上，将内容进一步升华。此外，还应了解学生的诉求，发挥学生的主体性，让学生自己梳理知识结构体系，在单元复习课中注意挖掘数学本质，感受知识发生、发展及应用的全过程，融入数学美及相应的数学文化背景，注重数学思想方法的渗透等。构建合理的认知结构，辅之一定的解题训练，定能更加高效地进行高中单元复习课教学，适应当前“双减”背景的教学要求。

参考文献：

［1］张奠宙，赵小平.难见好的复习课［J］.数学教学，2010（4）：封四.

［2］叶立军，陈莉.初中数学复习课教学存在的偏差及其应对策略［J］.教学与管理，2013（15）：91-93.

［3］杨汉鑫.高中数学有效复习课教学策略［J］.数学教学通讯，2021（18）：28-31.

［4］张奠宙，赵小平.教学中多多关注“后半段”：怎样上好复习课？［J］.数学教学，2011（4）：封四.

［5］曹才翰，章建跃.数学教育心理学［M］. 3版.北京：北京师范大学出版社，2018：138-149.

［6］张奠宙.复习课的设计需要理论建设［J］.数学教学，2015（2）：封四，36.

［7］章建跃.章建跃数学教育随想录：下卷［M］.杭州：浙江教育出版社，2017：771.

［8］克莱因.高观点下的初等数学：第一卷：算术 代数 分析［M］.舒湘芹，陈义章，杨钦樑，等译.上海：复旦大学出版社，2008：内容提要.

［9］罗声雄.数学的魅力：初等数学概念演绎［M］.武汉：武汉出版社，1999：215.

［10］张奠宙，邹一心.现代数学与中学数学［M］.上海：上海教育出版社，1990：32-36.

［11］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［12］夏敏，田静，王欣.中学生数学课堂核心能力的培养［M］.长春：吉林人民出版社，2019：66.

［13］叶晶，陈清华.基于内外部表征的数学高考应用题分析［J］.数学教育学报，2014（4）：92-95.

［14］代钦.数学教学论新编［M］.北京：科学出版社，2018：124.

［15］张文俊.数学欣赏［M］.北京：科学出版社，2011：55.

（责任编辑：潘安）