VIENNA整流器及其控制策略研究

徐成午,宋喜良,陈凯翔

(中国船舶集团有限公司第八研究院,江苏 扬州 225101)

0 引 言

随着电力电子器件与技术的发展,船舰系统对于整流器性能的要求也不断提高[1]。VIENNA整流器相较于其余三电平整流器所需的开关器件更少,拓扑结构简单,功率密度更高;相较于两电平脉宽调制(PWM)整流器,开关器件的耐压要求更低,更符合大功率装置的需求,同时还能进一步降低谐波含量,减少系统损耗。此外,由于VIENNA整流器的上、下桥臂在工作时不会同时导通,故其驱动信号不存在死区问题,运行更可靠稳定。因此,研究VIENNA整流器及其相关控制策略很有价值[2]。

1 工作原理与数学模型

1.1 工作原理分析

VIENNA整流器根据其直流侧电容中点是否与三相输入电源中性点相连可分为三相四线制与三相三线制2种拓扑结构。本文考虑到三相三线制结构无需引入中性线,从而不会被应用场合加以限制,故选择其作为研究对象,其拓扑结构如图1所示[3]。

图1 VIENNA整流器拓扑结构图

该拓扑结构主要包含三相对称输入电源ea、eb、ec,交流侧输入升压电感La、Lb、Lc,快恢复整流二极管D1～D6,3组可以实现电流双向流动的可控开关以及直流侧输出电容C1、C2。其中,由2个反向串联的MOSFET组成的可控双向开关在工作过程中需要同时动作。

用理想开关来替代双向开关即可得到该拓扑结构等效原理图,如图2所示。通过对Sa、Sb、Sc导通与关断状态的控制调节,可实现交流侧输入电流对交流侧输入电压波形的跟踪及直流侧输出电压大小的调节。

图2 VIENNA整流器的等效原理图

在VIENNA整流器正常工作过程中,交流侧三相输入电流的方向以及Sa、Sb、Sc不同的开关状态组合会影响到电路的工作状态。在进行工作原理分析时,关于电流方向,考虑到该结构中的a、b、c三相完全对称,故可将每个工频周期的ea、eb、ec按时间等分为6个区间,每个区间中都有两相的极性相同且与第三相相反,VIENNA整流器在每个区间内的工作原理是类似的,在此仅以ea>0、eb<0、ec>0的区间为例进行分析,将电流流出电网的方向作为正方向,则Ia>0、Ib<0、Ic>0;关于Sa、Sb、Sc的开关状态组合,共有8种不同的组合方式,对应的工作状态如图3所示,图中加粗线表示有电流流过,箭头方向即为电流方向。

图3 不同开关组合下的电流流向

1.2 数学模型建立

为使VIENNA整流器能达到相对优质的控制性能,需先建立其数学模型。考虑到网侧输入电流的方向以及不同的开关状态组合会导致不同的工作状态,为了方便分析,定义开关状态量为Sx来表示第x相的开关状态及电流方向,则有:

(1)

VIENNA整流器的等效电路如图4所示。图中Ra、Rb、Rc表示电路的等效电阻,大小相等为R;La=Lb=Lc=L;单刀三掷开关即为开关状态量Sx;电路的上、中、下3个桥臂分别用P、O、Q表示,如SbP= 1代表拓扑结构中的D3导通。

当三相交流电源对称时,对图4中电路列基尔霍夫方程组并使用状态空间平均法可得VIENNA整流器基于自然坐标系的数学模型的状态矩阵:

图4 VIENNA整流器的等效电路图

(2)

(3)

(4)

B=diag[1 1 1 0 0]

(5)

(6)

(7)

再进行Clark变换及Park变换可得VIENNA整流器基于dq旋转坐标系的数学模型:

(8)

2 控制系统设计

2.1 VIENNA整流器的空间矢量脉宽调制(SVPWM)控制

2.1.1 VIENNA整流器的空间电压矢量

由于每个Sx都有1、0、-1 3种状态,根据33=27种开关状态组合可推出对应交流侧电压值,还可合成出相应的空间电压矢量。由于三相电流不可能全同向,故[1 1 1]和[-1-1-1]2种状态组合在实际中不存在,因此得到的空间电压矢量的分布如图5所示,可将其分为区间Ⅰ～Ⅵ,每个区间都是1个等边三角形,再将每个区间分成4块区域,每块区域也都是1个等边三角形。

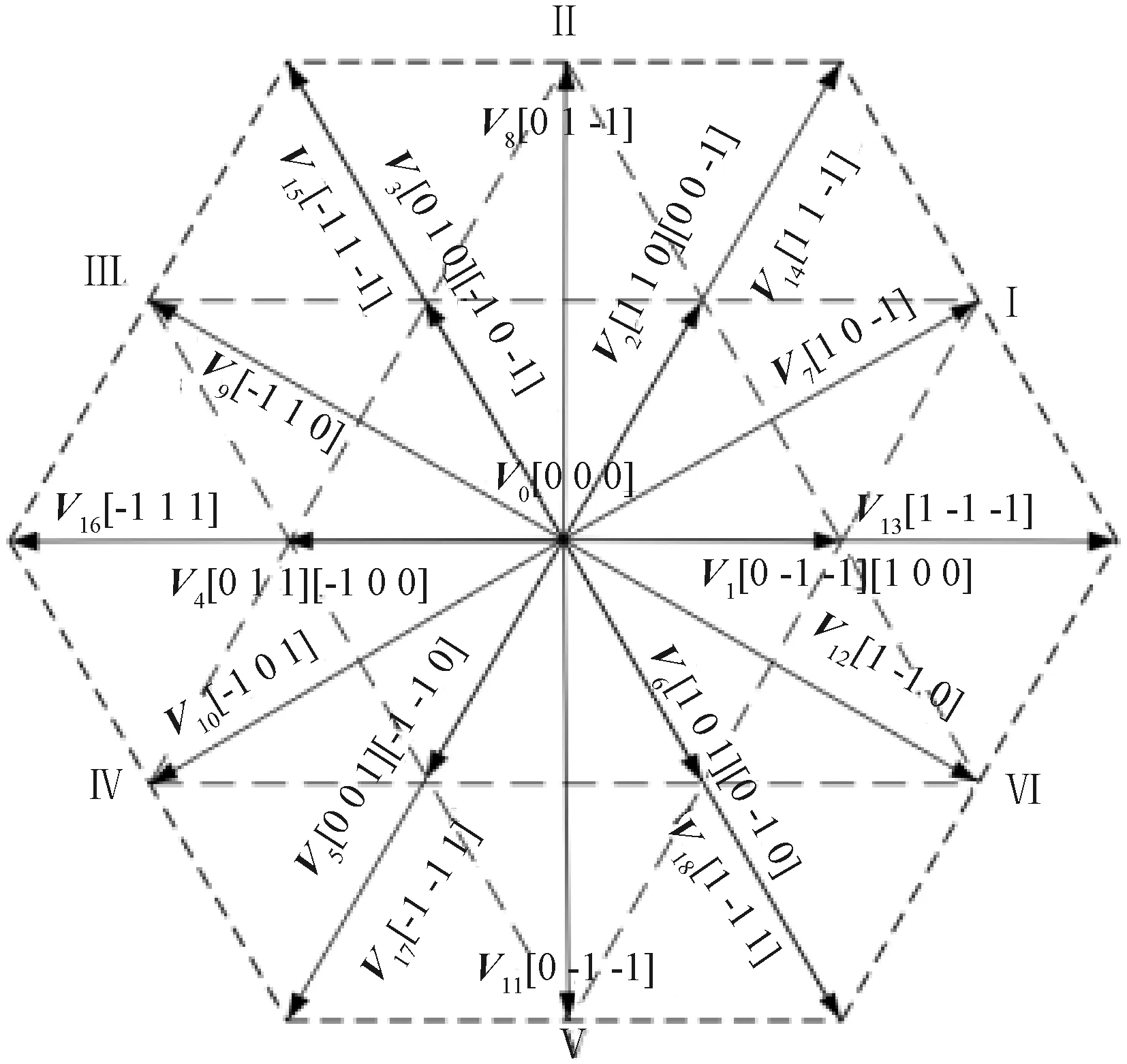
图5 空间电压矢量分布图

可将所有的基本空间电压矢量按照各自幅值的大小进行分类,如表1所示。

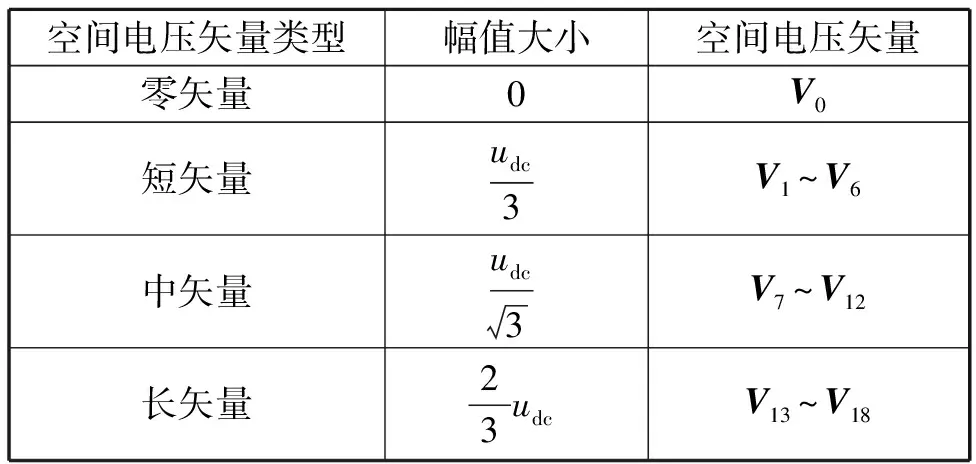
表1 空间电压矢量的分类

2.1.2 三电平SVPWM控制的简化

根据对VIENNA整流器拓扑的分析可知,电流极性状态会制约用于合成的空间矢量能否实现,即电流矢量的实时位置决定了在该时刻能实现的开关状态组合。故在进行SVPWM控制时必须判断电流的方向从而排除无效的矢量,而这必然会提高SVPWM控制的难度。若能将三电平的SVPWM等效转化为两电平的SVPWM,则可以达到简化SVPWM控制的效果。

将图5根据电流的极性状态进行区间划分,如图6所示。区间一至六在各自区间范围内时,电流的极性状态是不会改变的,则能实现的空间矢量也不会改变。当V*处于电流区间一内时,有ia>0,ib<0,ic<0,则Sa只可能等于1或0,Sb、Sc只可能等于0或-1,此刻能实现的矢量仅有V6[0-1 0]、V12、V1(2种)、V13、V7、V2[0 0-1]以及V0,这些矢量的终点形成了一个正六边形。

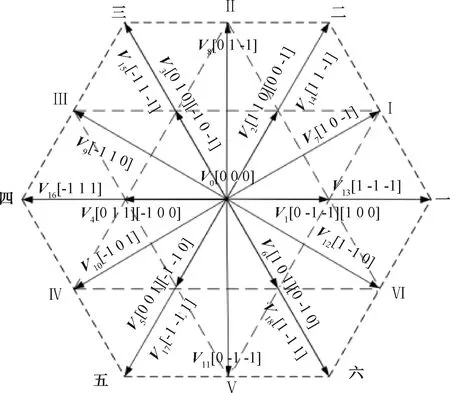
图6 按电流极性划分的矢量图

将三电平的SVPWM转为两电平的SVPWM的本质就是在判断出V*所处的电流区间后,再将V*等效变换为该正六边形的电流区间中的V*',然后对V*'进行两电平的SVPWM控制。关于V*所处电流区间的判断见表2。

表2 电流区间的判断

在此以V*位于电流区间一内时为例进行分析,如图7所示。

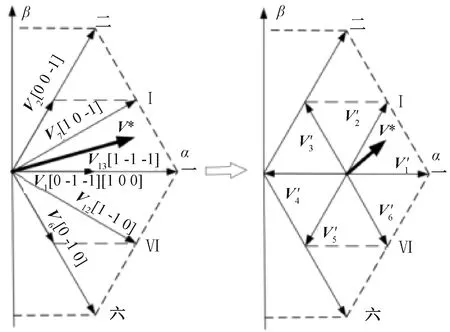
图7 三电平到两电平的等效变换

根据上述分析,V*处于电流区间一内,能实现的矢量有V6[0-1 0]、V12、V1(2种)、V13、V7、V2[0 0-1]以及V0,将它们分别减去电流区间一的短矢量V1得到的就是V0′～V6′,其中V0′为零矢量,如图7所示。V0′～V6′与V6、V12、V1、V13、V7、V2的终点形成的正六边形共同组成了一个等效的两电平空间矢量平面。而V*减去电流区间一的短矢量V1得到了在两电平平面等效的V*′。

同理可处理V*以及V*′处于其他区间的情况。

2.2 电容中点电位的平衡控制

2.2.1 电压矢量对中点电位的影响

在此仍以V*位于电流区间一内时为例进行分析。

零矢量:当V0作用时,中点并无电流流经,因此对O点的电位没有影响。

短矢量:当V1[0-1-1]作用时,ia流入中点O,C1放电且C2充电,这会导致uC1降低而uC2升高,即O点的电位在上升;当V1[1 0 0]作用时,电流流出中点O,C1充电且C2放电,会导致uC1升高而uC2降低,即O点的电位在下降。

中矢量:当V7作用时,uC1与uC2的大小变化由三相电流的大小及方向而定,也会对O点的电位有影响。

长矢量:当V13作用时,中点也无电流流经,因此对O点的电位也没有影响。

2.2.2 中点电位的平衡控制

要控制中点电位的平衡,从硬件角度研究,可以在C1、C2上各并联一个电阻从而进行均压处理或者增加独立开关对二者充放电,但会因为产生额外损耗而使整流器效率降低;从软件角度研究,零序电压注入法的调制难度较大,而正负冗余小矢量控制法可以根据2.2.1节中各矢量对中点电位的影响的分析来利用其实现对中点电位的平衡调节。

3 仿真与实验

使用Simulink软件搭建VIENNA整流器的仿真模型,设置参数为:输入线电压有效值380 V(50 Hz),开关频率100 kHz,交流侧电感0.8 mH,直流侧电容上下各4 000 μF,直流侧电阻10 Ω,直流侧电压给定值600～800 V。

当输出电压给定值udc*为700 V时,udc*及输出电压udc的仿真波形如图8所示,可以看出能提供稳定的期望直流输出。图9为此时a相的输入电压、电流的仿真波形,可以看出二者的相位相同,其余两相的波形也是如此。

图8 udc*与udc仿真波形图

图9 a相输入电压与电流仿真波形

图10 无电容中点电位平衡控制

图11 有电容中点电位平衡控制

按照图8的仿真模型搭建实验样机,电路参数与仿真基本相同。控制器选用数字信号处理(DSP)芯片TMS320F2802,开关管选用STW43NM60,二极管选用RHRU50120。实验结果如图12、图13所示。

图12 电压电流波形

图13 上下电容电压

可以看出:当设定输出直流电压为800 V,直流侧上下负载电阻分别为35 Ω和40 Ω时,上下电容的电压差值仅为2.27 V,实现了较好的中点电位平衡效果。

4 结束语

当VIENNA整流器在本文研究的控制策略下稳定工作时,不仅能稳定输出期望电压值,而且网侧输入电流为正弦波形,电流谐波含量极少,对电网几乎无污染,整流器工作在单位功率因数状态,对电网电能利用率高。此外,SVPWM控制的难度得到了简化,同时也实现了直流侧电容中心电位的平衡控制。