空间坐标转换程序设计与实现

王继红 李俊杰

摘要：空间坐标的转换有利于多坐标系统下的数据统一，各个用户之间的数据共享，是测绘过程中经常遇到的实际问题。基于泛在测绘对测绘仪器和工具去专业化的必然要求，該文通过VB语言编写了界面简洁、操作方便、功能全面的坐标转换软件，并通过实例数据验证软件可靠性，评定了转换精度。该坐标转换工具克服了算法复杂、操作繁琐、功能单一等缺陷，精度满足大多数工程应用中的坐标转换需求，可提供便捷、全面、可靠的服务。

关键词：坐标系  坐标转换  数据共享  精度评定

中图分类号：P226.3   文献标识码：A

Design and Implementation of Spatial Coordinate Conversion Program

WANG Jihong1  LI Junjie2

（1. Hunan Huawei Survey and Design Co.， Ltd.， Loudi， Hunan Province， 417000 China；

2. Bazhong Emergency Management Bureau， Sichuan，  Bazhong， Sichuan Province， 636000 China）

Abstract： The conversion of spatial coordinates is conducive to the unification of data under the multi-coordinate system and data sharing among users， which is a practical problem often encountered in the process of surveying and mapping. Based on the inevitable requirement of universal surveying and mapping for the deprofessionalization of surveying and mapping instruments and tools， this paper compiles a coordinate conversion software with simple interface， convenient operation and comprehensive functions through VB language， and verifies the reliability of the software and evaluates the conversion accuracy through example data. This coordinate conversion tool overcomes the defects of complex algorithm， cumbersome operation， single function， etc.， and the accuracy meets coordinate conversion requirements in most engineering applications， which can provide convenient， comprehensive and reliable services.

Key Words： Coordinate system；Coordinate transformation；Data sharing；Precision assessment

CGCS2000（2000国家大地坐标系）是定义在ITRF97框架下的区域性地心坐标系统，是目前中华人民共和国自然资源部强制要求全面采用的大地坐标系统[1]。

随着智能时代的来临，泛在测绘正在发展以实时精准时空感控为特征，以实现陆海天空网一体化、室内外一体化，并实现人与物理世界及虚拟网络世界交互的感知、探測、认知和调控[2]，将不同来源的空间数据统一在CGCS2000空间坐标系中，是测绘实践中常常遇到的问题[3]。而移动互联、5G通信、大数据、云计算、人工智能等新兴技术和测绘地理信息技术的不断交叉融合，测绘地理信息的相关应用和服务正向着千行百业拓展[4-5]。越来越多不同行业的工作人员、甚至普通民众都参与测绘数据的采集和应用，测绘仪器和工具的去专业化是泛在测绘的必然要求[6]。

目前能实现坐标转换的软件比较多，但往往算法复杂[1，7]，或者操作繁琐，要么功能单一，迫切需要一款界面简洁、操作方便、便捷实用、功能全面又能满足一般情况下精度要求的坐标转换软件。该文正是基于以上背景，设计了空间坐标的转换程序并用VB语言加以实现。

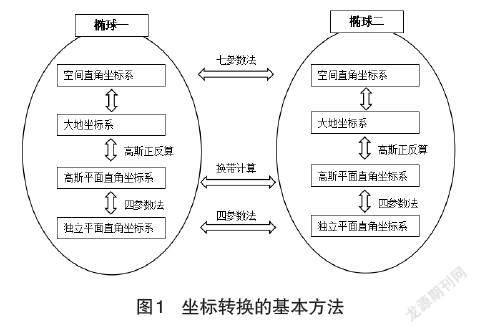
1坐标转换的基本方法

坐标转换主要包括在同一参考基准下的坐标转换和在不同参考基准下的坐标转换。坐标转换示意图如图1所示。

1.1大地坐标与空间直角坐标之间的转换

大地坐标（B，L，H）向空间直角坐标（X，Y，Z）的转换公式：

式中，N为该点椭球卯酉圈曲率半径；e为参考椭球第一偏心率。

空间直角坐标（X，Y，Z）向大地坐标（B，L，H）的转换公式：

式中，L可以直接计算求得，B可由迭代计算法求得。

1.2高斯正反算

高斯正算是将大地坐标（B，L）转换为高斯平面直角坐标（x，y）的计算过程。高斯投影具有正形投影的性质，并且考虑到投影后的中央子午线长度不变且仍然为直线，将函数展开为经差的幂级函数。公式如下：

1.3四参数法

两个不同的平面直角坐标系统通过四个参数（两个平移参数（△x、△y），一个旋转参数（α），一个尺度伸缩参数（k）搭建函数关系，可以实现这两个平面坐标数据的统一。函数关系式如下所示：

如果已知4个参数，则可直接将4个参数引入方程，再根据原平面坐标来求解转换后的所需坐标。如果参数提前未知，则可以利用两个平面坐标系上的公共坐标来求解四参数，公共坐标点个数不少于两个。若公共点个数大于2个，可按照最小二乘原理，通过间接平差方法解算四参数。

当公共点坐标数量为n个时，按照间接平差写出误差方程，则误差方程如下所示：

1.4 七参数法

七参数法是实现不同空间直角坐标系坐标转换的方法，其中布尔沙模型最为常见。其中包含3个平移参数（），3个旋转参数（即3个欧拉角，），1个尺度参数（k）。若已知七参数，则可直接引入七参数到下式（14），进行解算转换坐标。若七参数待求，则选取三个或三个以上的公共点按照最小二乘原则计算七参数。

2坐标转换的功能实现

基于VB6.0程序开发设计软件，在设计实现空间数据坐标转换程序中，主要分为实现同一椭球体坐标基准下不同坐标系下的坐标转换与实现不同椭球坐标基准下建立的坐标系下的坐标转换两大部分。主窗体界面及两大部分功能内容如图2所示。

此次设计的坐标转换软件将前述4个基本理论方法编写成子过程，当要实现某一个坐标转换功能时，采用调用子过程的方式来实现。对于某些功能可调用多个子过程。

在数据格式方面，输入大地经度和大地纬度时，为方便输入，提高效率，输入格式统一为“度.分秒”，例如12°23′45.6″的输入内容就为“12.23456”。并且为与输入方法对应，输出的格式也为“度.分秒”形式。无特殊说明下，长度单位为米（m），角度单位为度分秒（°，′，″）。

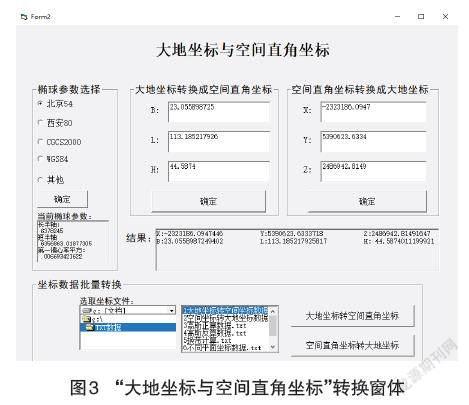
2.1 “大地坐标与空间直角坐标”相互转换的功能实现

当选择从大地坐标（B，L，H）到空间直角坐标（X，Y，Z）转换时，调取大地坐标转换为空间直角坐标子过程，即可实现大地坐标向空间直角坐标的转换。反之，调用空间直角坐标转换为大地坐标子过程，便能实现空间直角坐标向大地坐标的转换。“大地坐标与空间直角坐标”功能实现窗体如图3所示。

2.2 “大地坐标与平面直角坐标”相互转换的功能实现

此功能也包括两部分的内容，选择大地坐标（B，L）向高斯平面直角坐标（x，y）转换时，调用高斯正算子过程，即完成该转换。反之，调用高斯反算子过程，可实现高斯平面直角坐标向大地坐标的转换。“大地坐标与平面直角坐标”功能实现窗体如图4所示。

2.3 “投影换带计算”的功能实现

高斯投影换带计算的功能实现，先调用高斯反算子过程计算出大地坐标值，这个过程的中央子午线采用原高斯平面直角坐标系所使用中央子午线。然后再调用高斯正算子过程计算出高斯平面直角坐标，这个过程的中央子午线采用新高斯平面直角坐标系所使用中央子午线。“投影换带计算”的功能实现窗体如图5所示。

2.4 “大地坐标之间”相互转换的功能实现

在本次设计的软件中，此功能的实现采用间接法计算实现，在参数求解上采用三对公共点的方法。首先是将两个椭球体下的公共点大地坐标数据通过调用大地坐标转换为空间直角坐标子过程，使数据都统一转换为空间直角坐标数据。然后调用求解七参数子过程，计算两个空间直角坐标数据的七参数。最后，对待转换的原大地坐标系上的坐标数据进行转换，首先也是通过调用大地坐标转换为空间直角坐标子过程得到空间大地坐标数据，然后通过前面已经求出的七参数作为转换参数，将原椭球体上的空间大地坐标数据转换为现椭球体下的空间直角坐标数据，最后再通过空间直角坐标转换为大地坐标子过程得到最终的结果。“大地坐标之间”功能实现窗体如图6所示。

3坐标转换实例验证

为使转换结果的精度达到毫米级，在长度单位为米（m）的状态下取到小数点后4位。而在地球赤道附近，为使纬度上的长度精度也对应到毫米级上，则大地纬度以秒（″）为单位的状态下取到小数点后五位，同样，大地经度上也取到小数点后五位。

此处仅讨论大地坐标与空间直角坐标相互转换、投影换带计算、大地坐标之间转换的精度评定三个部分。

3.1“大地坐标与空间直角坐标”相互转换的精度评估

北京54坐标系下，点A大地坐标为（23°05′58.98725″，113°18′52.17926″，44.5874），空间直角坐标为（-2323186.0947，5390623.6334， 2486942.8149）。转换后的坐标对比数据如下所示表1、表2所示。

从上述两表的对比数据可以看出，该功能实现的大地坐标与空间直角坐标的转换精度严密可靠。

3.2“投影换带计算”的精度评估

换带计算的验证数据采用西安80坐标系下，中央子午线为117°下高斯平面直角坐标为点B（3102979.191，827982.595），其转换为中央子午线123°下高斯平面直角坐标参考值为点B′（3101364.1438，237656.2178）。

将上述的转换值再进行反算回去，得出的B″值与B值相对比，可进一步进行可靠性验证。其对比结果如表4所示。

从上表3、表4可以看出，高斯投影换带计算的精度较高。

3.3“大地坐标之间”转换的精度评定

选用西安80坐标系上五个坐标点向CGCS2000坐标系上转换为例。采用直接输入七参数法进行坐标计算，七参数列表如表5所示。计算结果误差表如表6所示。

由上述表6数据可知，转换误差在厘米级，精度能满足大多数工程应用。

4 结语

该文针对当前市面上教学和生产作业的坐标转换软件大都功能单一、操作繁琐、不便于学习与使用的问题，作者设计了此坐标转换软件。该软件可实现高斯正反算、换带计算、不同常用大地坐标系之间的大地坐标转换等多个功能，并且页面直观简洁、操作方便、结果准确。

经过系列精度评定，该坐标转换软件在同一参考基准下的转换严谨细致，在不同坐标基准下的坐标转换精度，可满足大多实际工程应用。本坐标转换工具可为地理信息方面的建设和应用提供便捷、全面、可靠的服务。不足之处在于不同坐标基准下的坐标转换精度不是很理想。究其原因，可能由于下面这几个因素的影响：（1）转换模型带有固定误差；（2）公共点坐标携带测量误差；（3）公共点数量不足。期望能在后续工作中加以改进与完善。

参考文献[1] 刘宝建，宋学忠. 区域CGCS2000坐标获取的欧拉矢量法[J]. 导航定位学报， 2022， 10（4）： 108-114.