双轴地磁辅助的惯性/卫星组合导航方法

赖玉敏, 宋嘉钰, 韩志强, 刘洪政, 游金川

（四川航天系统工程研究所, 成都 610199）

0 引言

旋转制导导弹是一种在飞行中绕自身纵轴连续旋转的导弹。 传统上, 旋转体制的导弹主要采用单通道控制, 利用舵面偏转产生的周期平均作用力控制导弹飞向目标［1］。 随着战争环境的恶化,攻防对抗更激烈, 对导弹高机动性能的要求不断加强, 具有更高控制效率的控制方案越来越多地应用在旋转弹上, 控制系统对弹体的姿态精度也提出了更高的要求。

惯性/卫星组合导航一般适用于倾斜稳定的导弹, 能够较为准确地提供弹体的姿态、 速度和位置信息。 而对于旋转弹, 由于其绕自身纵轴旋转,直接利用陀螺仪测量滚转角速率将引入很大的误差（尤其对于低成本的MEMS 陀螺仪）［2］, 因此常利用地磁传感器测量旋转弹的滚转姿态。 文献［3］利用旋转弹体本身动力学模型与安装在弹体横截面的双轴地磁传感器输出分别构建状态方程和量测方程, 通过扩展Kalman 滤波（EKF）实现了精度约10°的弹体滚转角估计; 文献［4］推导出了弹体滚转角速率与磁阻滚转角速率的关系式, 指出弹体滚转角速率的精度受俯仰角、 偏航角以及射线等因素的影响; 文献［5］根据坐标变换关系建立了联立方程式, 推导了弹体滚转角解算公式, 在射向大于15°时, 滚转角误差高达20°。 上述方案表明,仅靠地磁传感器测量滚转角存在较大的测量误差,因此也有学者研究地磁传感器与惯组的组合测量滤波算法［6-8］, 但由于地磁传感器仅提供姿态信息,惯性导航计算所得的速度、 位置无法得到校正。

本文提出了一种适用于旋转弹的双轴地磁辅助惯性/卫星组合导航方法, 能够同时精确计算出导弹的姿态、 速度以及位置。 利用安装在弹体横截面的双轴地磁传感器输出的两个地磁分量作为姿态观测量, 与卫星导航提供的位置、 速度观测量共同构建滤波器观测方程。 为解决卫星导航接收机与地磁传感器信息输出周期不一致的问题,本文采用序贯Kalman 滤波实现两个不同信息源的信息融合。 由于方案中, 地磁传感器为安装在弹体横截面的双轴地磁传感器, 因此也具有地磁标定简单、 对弹道要求低的优点。

1 地磁场模型

在靠近地面空间内的无源区, 主磁场可以表示为标量磁位V, 将其展开成如下的球谐函数表达式［9］

式（1）中,a为参考球半径;r为离开地心的径向距离,r=a+h;h为海拔高度;θ为地理余纬;λ为地理经度;pmn（cosθ）为n阶m次的缔合Legendre 函数（施密特准归一化的n阶m次Legendre 函数）。 利用IGRF 提供的地磁球谐项系数可计算北-天-东地理系下的地磁分量, 如下所示

对于近程导弹, 地磁场在地理坐标系与发射坐标系中的转换关系如图1 所示。

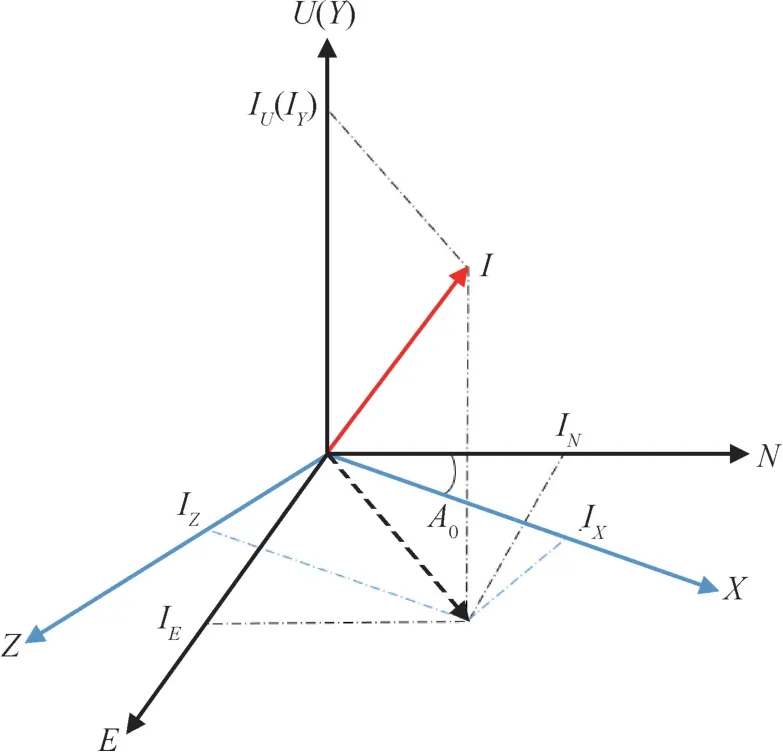
图1 地磁场在不同坐标系下的投影Fig.1 Projection of geomagnetic field in different coordinate systems

式（5）中,A0为发射方位角, 定义为发射方向与真北方向的夹角。

2 双轴地磁传感器姿态测量方案

双轴地磁传感器安装在过弹体质心的横截面内, 可敏感弹体法向和横向的地磁分量与, 如图2 所示。 在无磁干扰的环境下, 传感器铅直磁场中滚转一周, 以Z轴输出为横轴, 以Y轴输出为纵轴, 理论上输出曲线应该是以原点（0,0）为圆心的一个圆。

图2 双轴地磁传感器安装示意图Fig.2 Installation diagram of two-axis magnetometer

由于地磁传感器受铁磁性物质或者其他设备引起的磁场畸变、 纬度漂移、 强磁干扰等影响,其输出曲线变为近似的椭圆, 且圆心相对原点偏移到了（ZOFF,YOFF）。 同时, 因为软磁干扰的不对称, 使得输出的椭圆绕中心旋转了角度θ, 因此使用前需进行标定和补偿。 对于双轴地磁传感器的标定补偿可采用常见的椭圆拟合法［10］, 由于地磁标定方法非本文重点, 因此椭圆拟合法在此不再赘述。

3 双轴地磁辅助惯性/卫星组合导航算法

3.1 建立导航系统状态量及状态方程

本文选择导弹发射坐标系为导航系, 以惯性导航系统的3 个位置误差、 3 个速度误差、 3 个姿态误差以及加速度计的零偏和陀螺仪的零漂作为状态量, 表示如下

式（6）中,δx、δy、δz为发射系下的位置误差,δvx、δvy、δvz为发射系下的速度误差,φx、φy、φz为姿态失准角,εx、εy、εz为陀螺仪常值漂移,为加速度计零位偏置。

根据捷联惯导系统误差模型, 可构建系统状态方程如下

F（t）满足

式（8）中,f代表发射坐标系,gr为地球引力加速度在地心矢径方向的投影,r为弹体与地心连线的距离,为地球自转角速度的反对称矩阵,为比力的反对称矩阵,为发射系相对于惯性系旋转角速度的反对称矩阵,为弹体姿态矩阵。

将式（7）进行离散化处理, 可得

式（9） 中,Φk,k-1为状态转移矩阵, 具体计算如下

式（10）中,I15×15为一个15 ×15 的单位阵,Ts为惯导更新周期。

系统激励噪声为高斯型白色随机向量序列,满足如下条件

3.2 建立包含位置、 速度及双轴地磁分量的量测方程

（1）建立双轴地磁分量的量测方程

双轴地磁分量的量测为计算得到的地磁矢量在本体系下Y、Z两轴的分量与安装于弹体横截面Y、Z两轴的地磁传感器测量得到的地磁分量之差

由此, 可将双轴地磁分量的量测方程写为

式（16）中,V1（k） 表示测量噪声, 为高斯白色随机向量序列, 且满足如下条件

量测矩阵H1（k）的计算如下

式（19）中,A2×3满足

式（20）中,ci,j为矩阵Cb f的第i行第j列, 由惯导解算得出。

（2）建立包含位置、 速度的量测方程

由此, 可将包含位置、 速度的量测方程写为

式（23）中,V2（k） 为卫星导航测量噪声, 建模为高斯白色随机向量序列, 且满足如下条件

量测矩阵H2（k）的计算如下

3.3 序贯Kalman 滤波算法步骤

本文采用序贯Kalman 滤波算法依次对多个测量数据进行量测更新, 从而实现不同周期多源信息的融合, 具体步骤如下［11-12］:

1）初始化状态量X（0）和协方差阵P（0）;

2）求取状态转移矩阵Φk,k-1, 并进行状态预测

3）求解协方差预测矩阵

4）依次对2 个测量数据进行量测更新

式（29） ～式（31）中,i=1, 2, 且令。

5）融合中心最终的估计为

4 算法仿真验证

4.1 仿真条件

采用某旋转弹为仿真对象, 利用Matlab 仿真生成外弹道飞行数据以及各弹载姿态传感器测量输出的理想数据。 按表1 所示的弹载传感器误差参数进行设置, 仿真生成弹载传感器的实际测量输出数据, 在此基础上进行弹体飞行姿态估计算法的仿真验证。

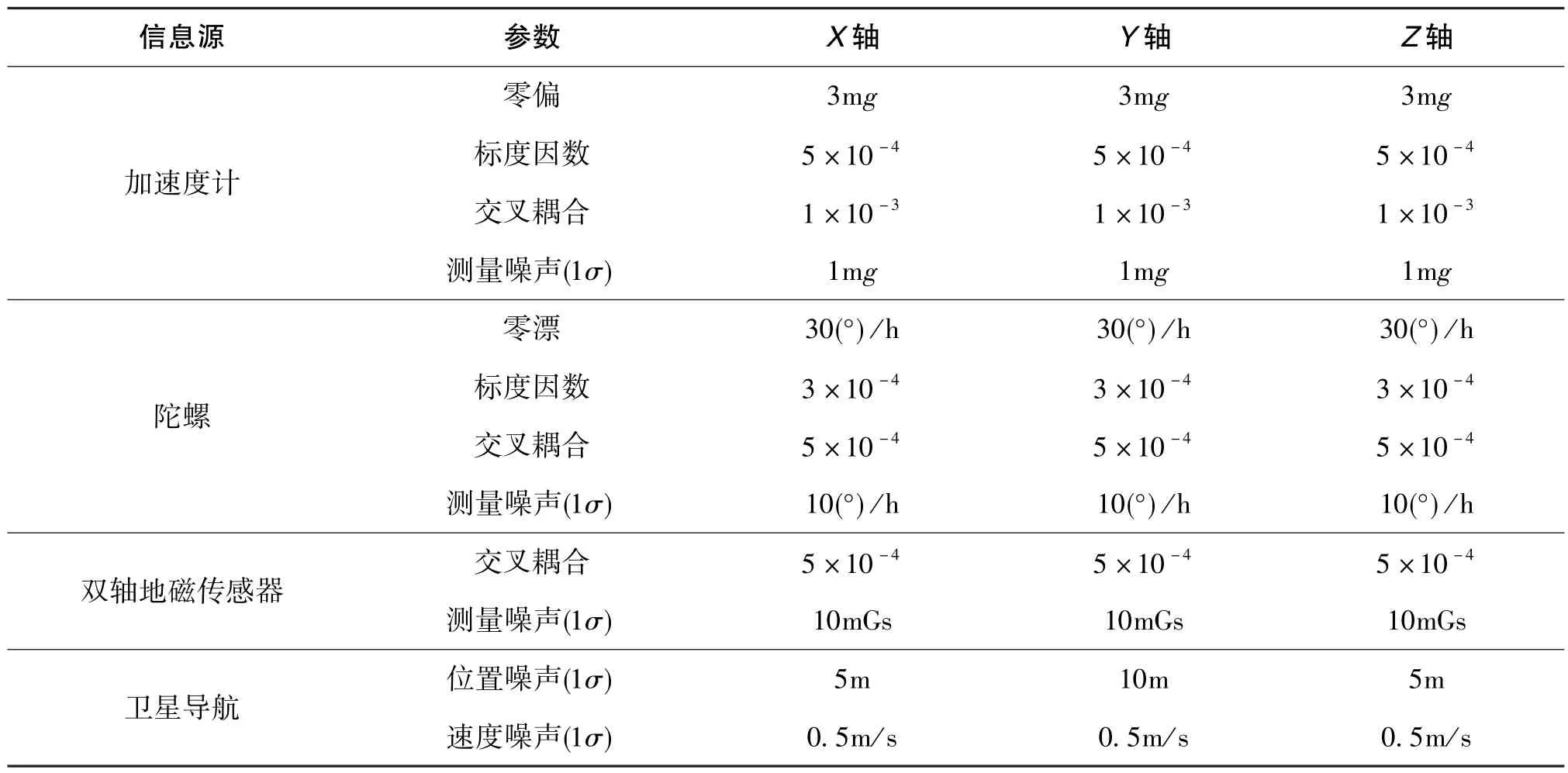
表1 传感器误差参数设置Table 1 Setting of sensor error parameters

导弹全程飞行时间约为65s, 弹体转速如图3所示。 导航解算初始俯仰角误差为10′, 初始滚转角误差为10′, 初始偏航角误差为18′。 捷联惯导解算周期为2ms, 双轴地磁传感器量测输出周期为10ms, 卫星导航量测输出周期为100ms。

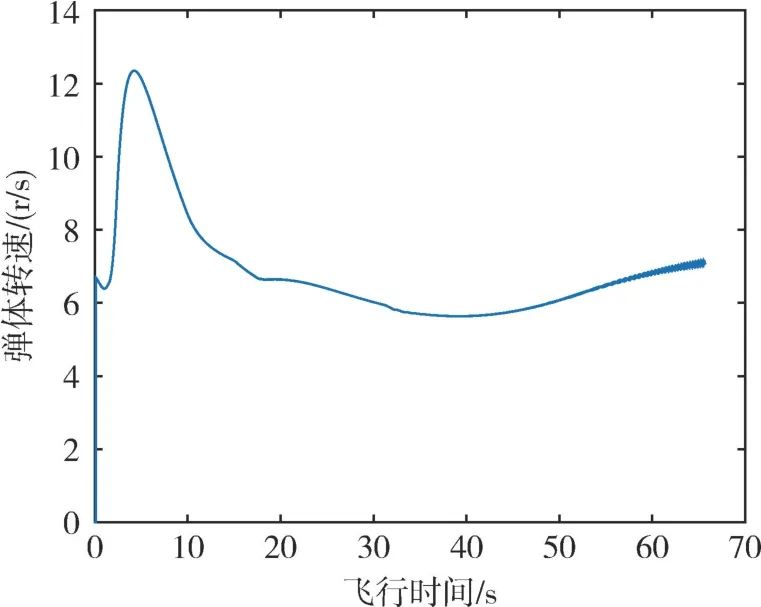
图3 弹体转速Fig.3 Roll rate of the projectile

4.2 仿真结果及分析

根据上述仿真设置的条件, 采用前述序贯Kalman 滤波完成对旋转弹飞行状态的估计, 其位置、速度以及姿态估计误差如图4 ～图6 所示。

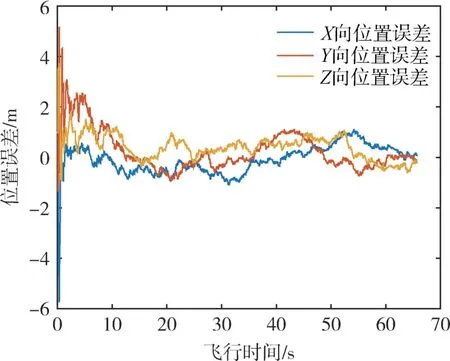
图4 位置误差Fig.4 Curves of position error

图5 速度误差Fig.5 Curves of velocity error

图6 姿态角误差Fig.6 Curves of attitude angle error

由图4、 图5 可知, 序贯Kalman 滤波将卫星导航测量噪声滤除, 从而获得较高精度的位置、速度估计。 滤波器稳定后, 三轴位置误差在2m 以内, 三轴速度误差在0.5m/s 以内。 经统计, 得到位置误差、 速度误差分别为1.46m、 0.15m/s（1σ）。

由图6 可知, 本文所述双轴地磁辅助的惯性/卫星组合导航算法与常规惯性/卫星组合导航算法在偏航角以及俯仰角的姿态估计上精度相当。 而对于滚转角的估计, 本文所述算法由于引入了反映滚转角信息的高频率双轴地磁传感器输出, 滚转角估计精度更优, 且在很短的时间可得到很好的收敛。 而采用常规的惯性/卫星组合导航算法,对于滚转角的估计需要近20s 才能收敛。 在滤波稳定后, 经统计利用本文算法获得的弹体滚转角、偏航角和俯仰角姿态估计误差分别为0.46°、0.47°和0.28°（1σ）。

5 结论

基于双轴地磁传感器、 MEMS 惯组和卫星导航的测量信息, 本文提出了一种适用于旋转弹的双轴地磁传感器辅助惯性/卫星组合导航方法。 以捷联惯导误差方程为基础建立了系统状态模型, 以双轴地磁传感器测量值与卫星导航接收机测量值分别建立了量测模型, 利用序贯Kalman 滤波实现了信息融合。 仿真结果表明, 该方法实现了较快的收敛速度和较高的精度, 但对于实际应用还有待验证。