航空双系统直驱伺服阀阀芯振荡机理及抑制方法
王彬,任鹏达,张伟,谢志刚,张文星
1.南京航空航天大学 江苏省航空动力系统重点实验室,南京 210016
2.南京航空航天大学 能源与动力学院,南京 210016
3.航空工业西安飞行自动控制研究所,西安 710076
飞机舵面、起落架及刹车等操控机构大多为电液控制系统,其性能对飞行稳定控制与安全至关重要。伺服阀因精度高、响应快等优点在飞机操控机构中获得广泛应用[1]。其组件多、工艺难度大、故障率高,给飞控系统性能提升带来了严峻挑战。高可靠、轻量化和高性能电液伺服阀是机载液压控制领域发展的重要课题[2]。
国内外针对伺服阀可靠性及典型故障开展了研究。伺服阀故障可表现为阀芯振荡和啸叫(一种尖锐噪声),严重时会导致液压系统性能恶化甚至引起灾难性后果[3]。伺服阀自激振荡是指阀内活动部件的自发振动,其频率可高达数百至数千赫兹。研究表明,自激振荡除与油源有关,还与流场中的瞬态空化和压力脉动密切相关[4-5]。Elsheikh[6]研究了平衡阀内的高频噪声,通过改进设计消除其不良影响。Ziada 等[7]对溢流阀和涡轮控制阀的振荡噪声研究发现,流体剪切层可能在伺服阀中诱发压力脉动和高频振荡。Gao 等[8]研究阀内涡流、能量损失、噪声和流体力,发现涡流形状和强度受阀开度影响,进而影响振荡形式和强弱。Li 等[9]通过数值模拟研究伺服阀内涡流变化对空化的诱发机理,揭示其与流体能量损失和噪声的内在关联。Liu 等[10]研究调节阀非定常空化流动过程和压力波动特性,认为阀芯结构参数对阀内空化和压力脉动有较大影响。Qiu 等[11]预测了节流阀内总气相体积,发现减小阀芯位移会导致气相区扩大和气相密度增加。Lindler 和Anderson[12]对直驱伺服阀的研究发现,阀芯小开度时的高压降易使流体流经时发生分离或汽化,导致阀芯出现振荡。
张鹤然等[13]以压力伺服阀为研究对象,分析了伺服阀振荡啸叫现象特征与产生机理,并提出调整挡板结构参数改变其阻尼的措施。Porteiro等[14]对平衡阀工作中的高频振动进行了湍流模型下二维流动仿真与试验,认为射流引起的压力脉动是高频振动的重要原因。同时,流场中的气穴、自振和剪切层振荡是阀类振动产生的主要原因。陆亮等[15]认为射流流域内的剪切层振荡是导致流体自激振荡的原因,以溢流阀为例分析其自激振荡产生机理。Yuan 等[16]对锥阀流场进行数值计算仿真,认为气穴产生的主要原因为流体剪切和流动分离。
随着伺服阀性能要求的不断提升,新结构原理的伺服阀也相继出现,如直驱伺服阀(Direct Driving Servovalve, DDSV)、多 路 伺 服 阀等[17-19]。另外,新型智能材料在电-机械转换器中的应用也是伺服阀的研究方向之一。彭畅[20]设计了直动式压电伺服阀和喷嘴挡板压电伺服阀并研究了其静动态特性。徐现荣[21]提出了一种基于形状记忆合金的微型气动伺服阀。李跃松[22]研究了一种超磁致伸缩射流伺服阀,实测了线性度、响应等指标并与传统伺服阀进行了对比。
传统两级伺服阀元件数量多、工艺要求高、可靠性低,成为航空液压系统故障率高的主要部件之一。近年来,在抗污染、高可靠伺服阀研究方面,直驱伺服阀成为主要热点之一[23]。其直接由电机驱动,驱动力大且可增加阀芯行程,提高了阀的抗污染能力。然而,对不同负载,直驱伺服阀需重新调试控制参数,耗时较长[24]。飞机舵面操控系统多为对称分布,往往需要两套电液伺服机构实现有时序的关联驱动。同一控制任务需要两套液压作动机构联合协同动作,不利于简化系统而保证可靠性。长期以来,航空飞行控制领域迫切需要一种可实现双系统或多系统操控的高可靠、大流量伺服阀,避免传统两级电液伺服阀放大能力有限、可靠性低的不足。直驱阀可用于飞机舵面液压作动机构。将直驱伺服阀双阀芯或三阀芯串联固结,可实现多系统同步驱动与控制。因双液压系统协同工作是飞机舵面驱动的独有特点,直驱阀可满足双系统乃至多系统的控制需求。同样功能下,直驱阀可大幅提高飞控系统功率密度且增加了机载部件的可靠性。主阀芯由电机直接驱动并构成位置闭环,有利于保证控制精度,已在部分飞机的舵面操控系统应用。
直驱方案虽然避免了多级阀级间油液流动,但传动件间的机械联结和双系统阀结构极易因刚度不足发生局部弹性变形或流固耦合诱发振荡。直驱阀阀芯振荡的影响因素诸多,如构件耦合振动、油液压力脉动等[25-26]。阀芯振荡导致作动筒和连接气动面高频抖动,影响液压作动器的调节过程,极易加速作动器疲劳失效,威胁飞行稳定和安全。因此,对直驱伺服阀阀芯振荡,需要通过研究揭示其发生发展机理,确定其关键影响因素,从设计上抑制或避免其发生,为高性能舵面操控机构设计打下必要的基础。
针对双系统直驱伺服阀阀芯振荡,提出一种与阀内空化具有对应关系的振荡机理模型。通过气液两相数值模拟获得典型工况下阀芯凸肩面上的压力脉动,基于阀芯动力学仿真复现了阀芯振荡。在仿真与试验基础上提出了抑制阀芯振荡的方法,为工程设计提供理论参考。
1 双系统直驱式伺服阀
1.1 工作原理
双系统直驱式伺服阀由直线电机、拉杆、阀芯、阀套及位移传感器等组成,如图1 所示。阀芯为两只四通阀连接为一体的结构,通过拉杆将其与直线电机连接。电机驱动阀芯时带动两组阀口变化,从而实现双液压系统的同步调节。位移传感器实时测量阀芯位移并反馈至阀控制器,以构成阀内闭环回路。阀套与阀口对应部位开有4处通油口,分别为供油口P、回油口T 及控制口A、B,阀套与阀芯构成非全周开口以满足最大开度内的节流边可控。

图1 双系统直驱伺服阀构成Fig.1 Architecture of dual-system DDSV
1.2 阀芯受力分析
滑阀阀芯受液动力、惯性力、黏性阻尼力、弹簧力及外驱动力等联合作用,而当阀芯上作用力的合力存在交变或脉动时则会使阀芯位置不稳定即出现振荡。关联阀芯受力如图2 所示,图中:Ft为电机驱动力;Ff为黏性摩擦力;Fp为油液空化产生的气穴附着力;Fk为两侧阻尼腔液压弹簧产生的液压恢复力;FL为液动力;v1、v2为阀腔进出口油液速度;p1、p2为阀腔两侧油液压力;pd1、pd2为两侧阀腔短暂封闭时油液压缩产生的压力。

图2 阀芯受力图Fig.2 Force diagram of spool
通常认为,同一阀腔内两侧凸肩对应受力面上的压力相等。但流场仿真显示,油液由一节流孔流入阀腔瞬时易发生空化,气泡随油液流动及自身发展、溃灭过程均可导致两侧凸肩面上的压力不稳定。另外,液动力是油液流经阀口时速度大小和方向变化对阀芯的反作用力,也直接影响阀芯的整体受力。因此,在阀芯动力学建模时,液动力的作用可并入凸肩面所受流体作用力。阀芯两端为阻尼腔,阀芯快速运动时可视作短暂封闭,腔内油液压缩形成液压弹簧效应,建模时也应考虑。这里阀芯受力主要包括阀腔凸肩面液压力、阀口液动力、两端阻尼腔流体等效的液压弹簧力、黏性摩擦力以及驱动力等。本文研究的双系统直驱伺服阀,当双阀处于同一开度时,阀芯同时受两组对应阀口凸肩面液压力和液动力的耦合作用。不同于单阀芯仅一个阀口压降较大,双系统直驱阀的双阀芯极易因对应阀口较大的匹配偏差使两大压降阀口产生的不稳定瞬态液压力叠加耦合,当两者合力克服电机驱动轴的弹性力等阻力即引起阀芯高频振荡。
2 阀内流动数值模拟
2.1 模型及边界条件
当局部压力达到特定温度下的饱和蒸气压,油液会发生汽化现象,产生的汽泡随液体从入口向外周流动时,又因压力突增而急剧冷凝。液体从四周急速冲向汽泡中心,产生较大的瞬时压力。节流是流量伺服阀的主要工作方式。阀腔内油液汽化主要发生在阀口及相邻凸肩垂直面附近。无背压时伺服阀回油口压力接近油箱压力,从伺服阀进入执行元件或执行元件进入伺服阀回油腔的油压与油箱压力相比较高。高压降阀口处的汽泡流入管路或执行元件,再由阀口进入回油阀腔,因此高压降诱发的空化对阀芯影响主要部分通常在回油阀腔内。
图3 为某开度时单系统直驱伺服阀阀口结构。图中,PA、PB分别为直驱伺服阀A、B 口油压。数值模型对应的回油腔网格如图4 所示。进油腔网格与之相似,仅流动方向和腔体尺寸不同。计算域模型网格数量为250 万,最低网格质量为0.4,后面将对网格无关性进行验证。因双系统直驱滑阀的2 个三位四通阀结构相同,不考虑因加工安装误差导致双阀芯受力不均而诱发的振荡,重点讨论空化对阀芯振荡的影响机制,即假定某一开度下两组滑阀流动状态相同。
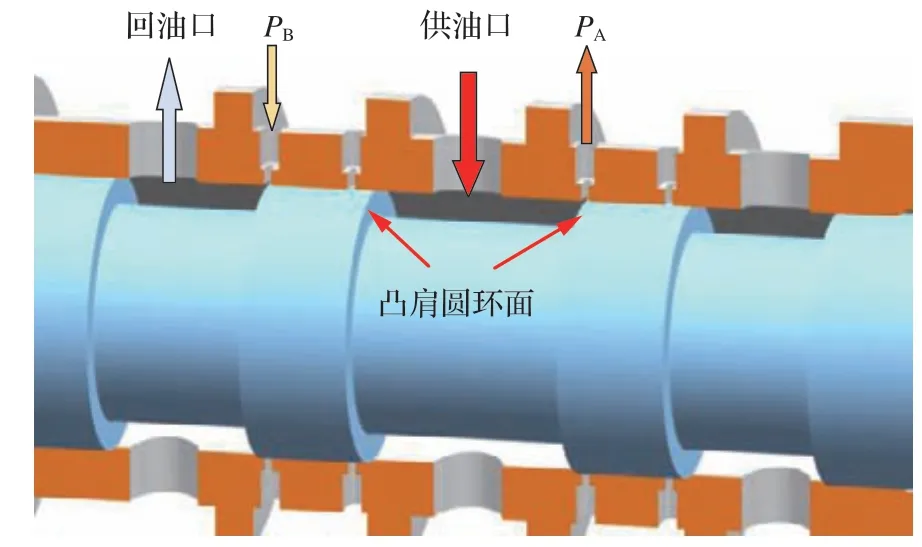
图3 单系统直驱伺服阀阀口结构Fig.3 Opening structure of single-system DDSV
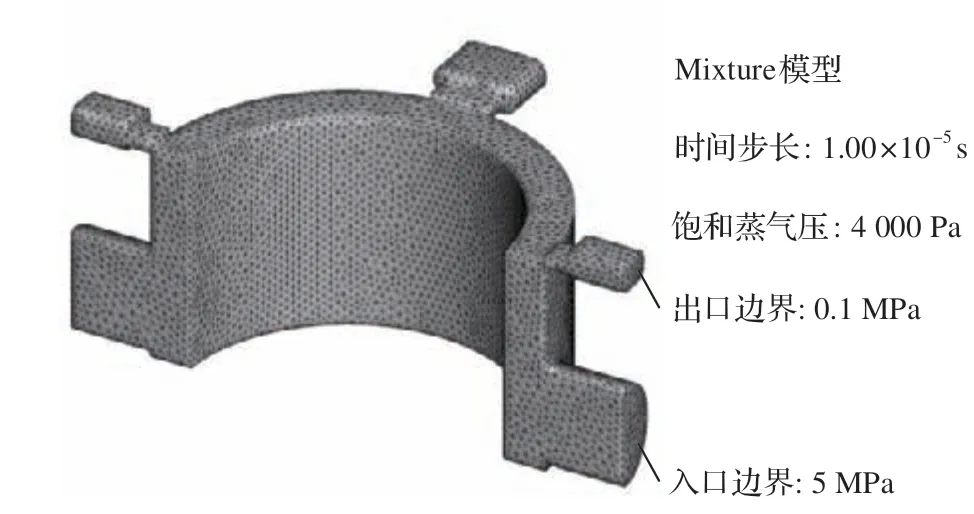
图4 回油腔网格及模型参数Fig.4 Meshes and model parameters for return cavity
典型描述流体微团运动的Navier-Stokes(N-S)方程:式(1)描述流体连续性,表示单位时间内控制体的质量变化等于该时间内流入控制体的净质量;式(2)为动量方程,描述单位时间内控制体的动量变化等于其所受的合力。
式中:xi、xj为流体微团地面坐标系两方向的坐标;ρ为单元体流体密度;ui、uj为相应速度分量;τij为应力张量;t为时间。
流场中空化产生或溃灭引起的相变及相间输运过程由Schnerr-Sauer 空化模型描述,见式(3)。该模型在复杂形状的多相流计算中较为稳定。计算中忽略不同相间的滑移速度,即假设紧邻的液汽两相运动速度相同。
式中:αv为气相体积分数;ρv、ρl和ρm分别为气相、液相和混合相介质密度;pv为饱和蒸气压,pm为混合相压力;Re和Rc分别为气相蒸发速率与凝结速率;RB为气泡直径。
数值模拟时求解器采用基于压力的SIMPLE 算法和二阶迎风离散格式。进油腔入口、出口边界分别为21 MPa 和7 MPa,回油腔入口、出口边界分别为5 MPa 和0.1 MPa。仿真条件设置与实验工况一致。数值模拟主要参数见表1。

表1 数值模拟主要参数Table 1 Main parameters for numerical simulation
2.2 结果分析
为验证数值模型的可靠性,提取仿真回油流量与实验值对比,如图5 所示。实验流量与不同网格数模型计算结果基本吻合,证明网格无关性及数值模型的可靠性。因出口压力高,进油腔内无气穴发生,而回油腔阀口附近存在气穴分布,如图6 所示。因高速射流自节流孔和阀口流入阀腔时冲击阀腔壁,射流两侧产生涡旋,油压不断降低至饱和蒸气压以下,诱发气泡析出,产生气穴。
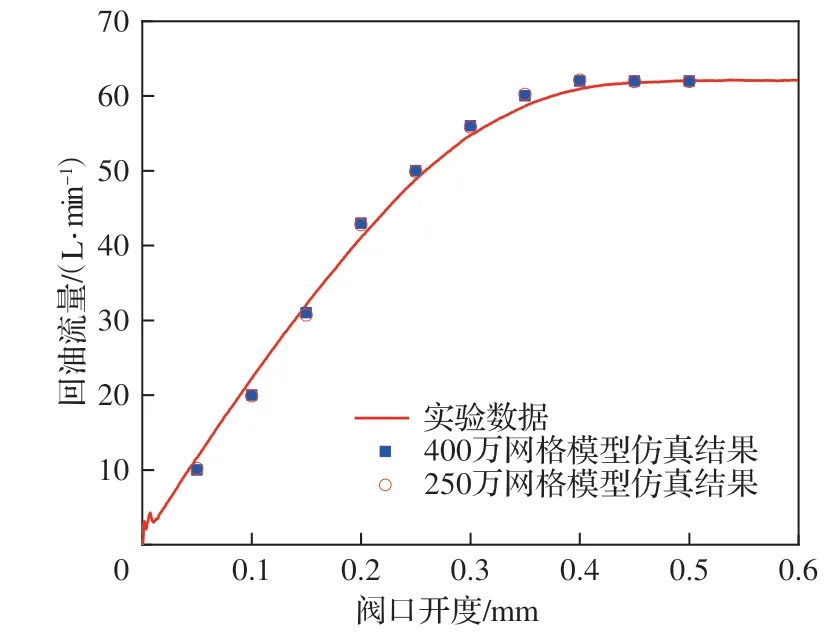
图5 回油流量Fig.5 Return flow rate
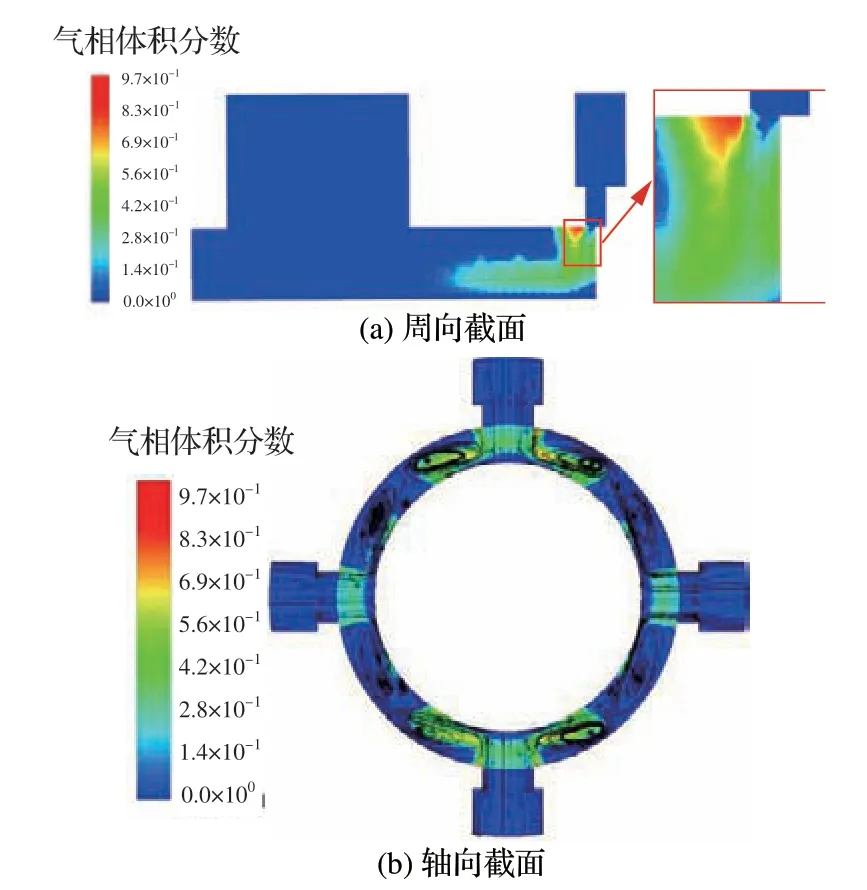
图6 回油腔气穴Fig.6 Cavitation in return cavity
为直观看出回油腔两侧凸肩面上的压力分布,图7 给出了不同时刻T回油腔两侧凸肩面压力分布,图中上方为远阀口侧,下方为近阀口侧,T为瞬时时刻。两侧瞬时压力并不完全相同,故阀芯振动模型需考虑油腔两侧压力差异及变化。图8 为回油腔近阀口一侧部分凸肩面上的压力与气相体积分数分布。可以看出,低压区与气穴区位置基本吻合,气穴区扩大时,低压区也随之扩大。由此得出,伺服阀阀腔内的压力脉动与气穴程度直接相关。
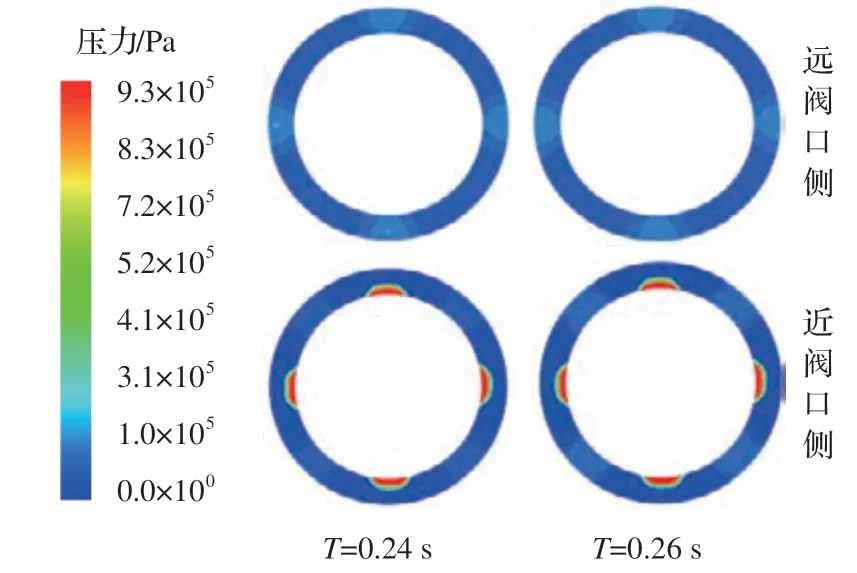
图7 凸肩面压力分布Fig.7 Pressure distribution on ring faces
为了进一步说明该问题,提取阀口凸肩面近域的平均压力和平均气相体积分数,其随时间变化规律如图9 所示。图10 中压力与气相体积分数的变化趋势对应,气相体积分数位于波峰时,压力处于最低点。取同一流域网格模型,分别计算有无气穴模型时阀腔凸肩面上的平均压力,图10 即为气穴对其影响曲线。图10 中看出,同一时间跨度内,有气穴模型时此处压力变化较为剧烈,且具有一定的规律性,呈反复升高或降低趋势;而无气穴模型时凸肩面上的压力基本稳定,波动范围远小于前者。这进一步验证了气穴发生易加剧流场不稳定,导致流域内压力波动,可通过两侧凸肩面传递至阀芯上,这是气穴诱发阀芯振荡的机理。
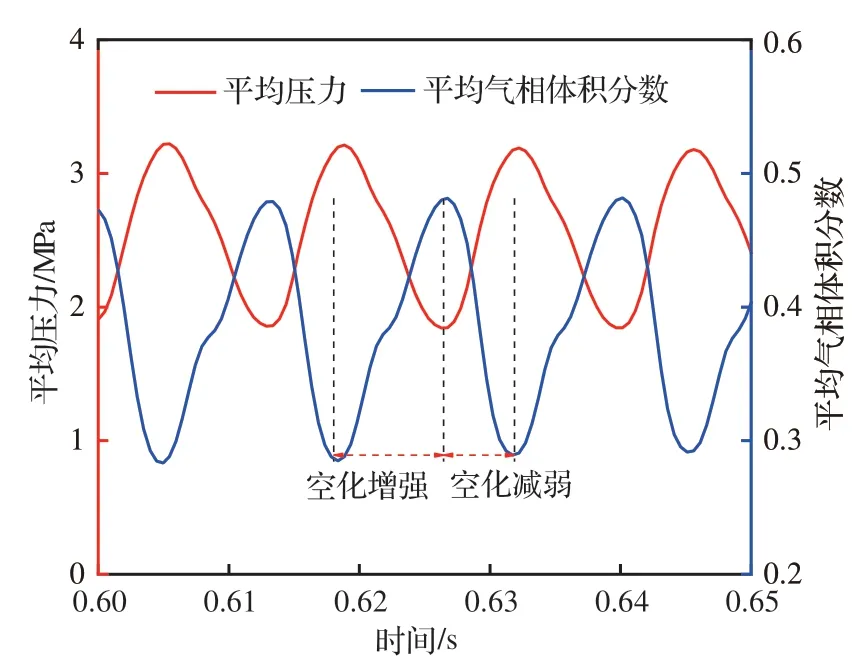
图9 凸肩面平均压力及平均气相体积分数变化规律Fig.9 Changing rule of mean pressure and mean vapor volume fraction on ring face

图10 气穴对凸肩面压力的影响Fig.10 Cavitation effects on pressure on ring face
由以上仿真结果知,气穴导致的阀腔流域压力振荡和不稳定流动可通过压力传递至阀芯凸肩面上,使阀芯位移受附加扰动。气穴产生机理是经过阀口节流加速后的油液在阀腔内产生高速涡旋,使其压力降低至饱和蒸气压以下。有研究表明,阀腔和节流口尺寸比是影响气穴发生的主要因素[27]。在此基础上提出两种改进设计方法,通过改进阀腔和阀口设计避免不稳定流动,以抑制阀腔内气穴发生。
双系统直驱伺服阀作为飞控系统中的关键控制元件,整阀长度一般受作动装置整体体积限制而难以调整。定义阀杆长径比为β=L2r,r为回油腔阀杆半径,L为回油腔阀杆长度,一定范围增加长径比可使回油阀腔容积有效减小,从而降低阀腔内的涡旋尺寸。
参照工程习惯选取阀杆长径比分别为0.67、0.55 和0.43,计算阀腔两侧凸肩面局部气相体积分布。图11 为3 种阀杆长径比时控制阀口一侧部分凸肩面上的气相分布。随阀杆长径比降低,凸肩面上气穴强度和范围均有所下降。阀杆长径比为0.43 时,仅在阀口下游附近存在少量气穴,且未向该凸肩面上的其他区域扩散。这是由于阀口压差一定时气穴形成的关键因素为阀口前后容腔的体积比。阀腔壁面与阀杆壁面间的距离不断减小使涡旋尺度随之减小,抑制了涡旋中压力的快速降低,使气穴程度有所缓解。
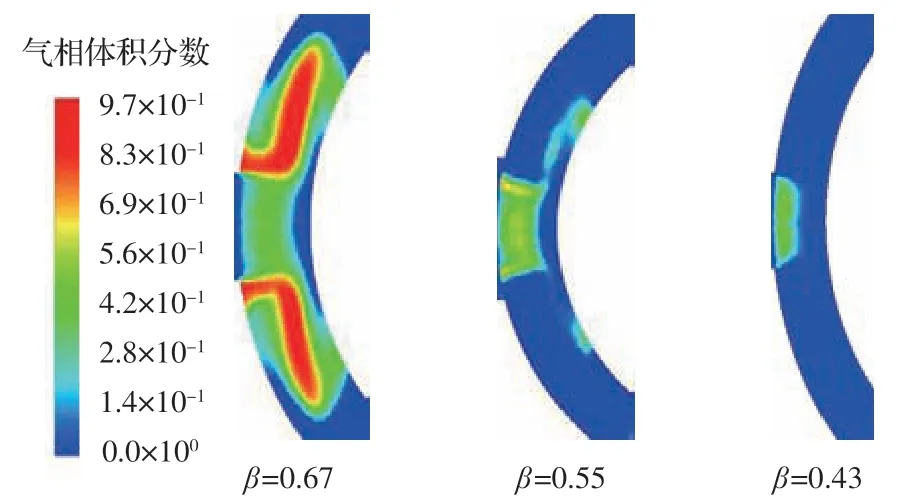
图11 不同长径比时部分凸肩面的气相体积分数Fig.11 Vapor volume fraction on partial ring face for different length-diameter ratios
除减小阀腔容积(长径比)外,通过改进阀口结构以改变油液流动状态也是抑制气穴发生的有效方法之一。为了满足可控阀口流量不饱和条件,常在无法增加阀腔容积时尽可能采用通流面积较小的非全周阀口,由此易诱发阀口气穴。电液伺服系统常工作在零位附近,控制阀阀口开度一般较小,更加剧了气穴的严重程度。针对二级节流阀口易出现气穴问题,提出了阀口前三级节流结构。该结构可使油液流经阀口时速度梯度降低,使流向与阀口方向不一致的油液流速大幅衰减。多级节流也可使其单级压降减小,油液流经阀口时更连续和稳定。图12 为三级节流阀口近域凸肩面气相分布的仿真结果。阀口后油液附着于凸肩面上的气相体积明显减小,且强度也大幅降低。图13 为不同阀口前节流级数的速度云图,油液流经三级节流阀口前后速度变化更小,且最高速度更低,改善了流动稳定性,有利于抑制阀口气穴的产生。
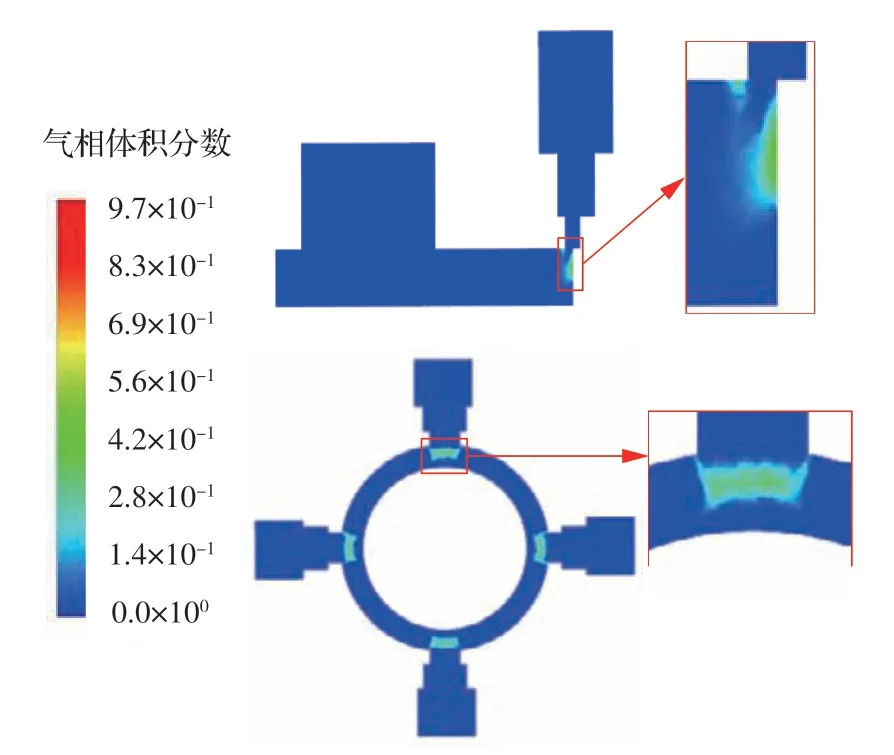
图12 三级节流阀口近域凸肩面气相体积分数Fig.12 Vapor volume fraction on ring face close to three-stage throttling port
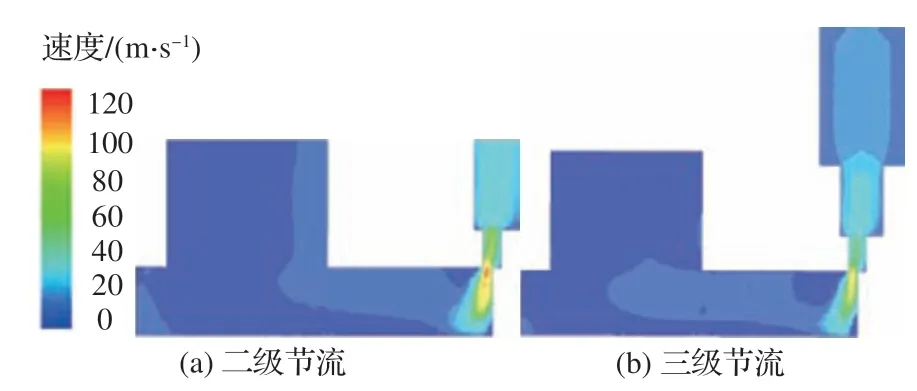
图13 不同阀口前节流级数的速度云图Fig.13 Velocity nephogram for different throttling stages upstream of opening
3 阀芯动力学分析
3.1 动力学建模
阀芯凸肩面上液压力受阀口附近阀腔内气穴影响具有时变特征,且整个环形面为气液两相共存。欲获得准确的阀芯瞬态受力,需考虑气穴附着力、阀口液动力、阀芯黏性阻尼力、惯性力及外驱动力。将阀腔两侧垂直凸肩环形面受到的油液、气泡作用在阀芯上的瞬时平均流体力统称为气穴附着力。因油液-阀芯双向流固耦合的全域数值求解难度大,采用数值模拟与数字仿真结合,将数值计算结果导入阀芯动力学数学模型中,与阀芯上的其他力共同构建动力学方程。其中,气穴附着力由数值模拟计算获得流场信息的数据集,其可看作气穴附着力动态阀口开度的函数。计算中通过差分方法获得当前时刻阀芯所受气穴附着力,根据相应方程计算获得阀口液动力、阀芯黏性阻尼力、惯性力和外驱动力,由其合力构建阀芯的动力学模型。
对有空化的阀腔瞬态流动,压力为与位置和时间有关的场函数,可表示为p(g, t),其中g为空间位置,t为时间。当网格i的位置为gi时,p(gi, t)可描述点i处的局部静压。在局部静压p(gi,t)的基础上,可以量化一个面所受流体的压力:
式中:N为该表面包含的网格单元数;p(i, t)为第i个网格单元的静压值;ΔS为求解面的面积。据此可以求得阀芯凸肩面的瞬时平均压力,即获得油液空化影响时凸肩面上的时变压力。
由动量定理知,流体对阀芯的稳态液动力为
式中:ρo为油液密度;q为流量;v1和v2分别为进口和出口速度矢量。FW可分解为径向分量和轴向分量。阀口为径向对称分布,则径向稳态液动力可相互抵消。设阀口处射流角为θ,则稳态轴向液动力大小为
瞬态液动力计算公式为
式中:l为阻尼长度。
则总的液动力为
直驱伺服阀阀芯与阀套间存在黏性摩擦力,其与阀芯运动速度近似成线性关系。但有文献表明,黏性摩擦力受速度变化影响较小,而受油液压差作用较大。进行动力学仿真时,整阀进口压力恒定,故考虑黏性摩擦力为定值[28]。电机驱动力则与阀芯上的运动阻力有关,考虑发生振荡时其在某一开度附近,因此仿真时设定驱动力在特定开度时不变。
综上,阀芯动力学方程可表示为
式中:Cf为阀芯运动的黏性阻尼系数;m为阀芯质量。
3.2 振荡仿真
基于动力学方程求解时,将CFD 数值计算获得的各凸肩面压力数据导入动力学模型,通过二维查表将CFD 与动力学方程联合,以准确描述不同时刻或阀芯不同位置时所受的气穴附着力及其对阀芯运动的影响。 伺服阀进口压力21 MPa,出口为大气压,阀芯质量0.2 kg,油液运动黏度20 mm2/s,体积弹性模量1 380 GPa。
图14(a)和图14(b)分别为有/无气穴附着力影响时阀芯位移振荡曲线。图14(a)中,阀芯位移振荡频率约180 Hz,振荡幅值约20 μm。而图14(b)中,不考虑气穴附着力时,阀芯位移振荡幅值仅5 μm 左右,对下游压力流量几乎不产生直接影响。仿真结果显示,阀芯位置主要由电机驱动力、两端油液形成的液压弹簧复位力决定,气穴附着力对阀芯振荡起主要作用,是阀芯振荡的主要诱导因素之一。
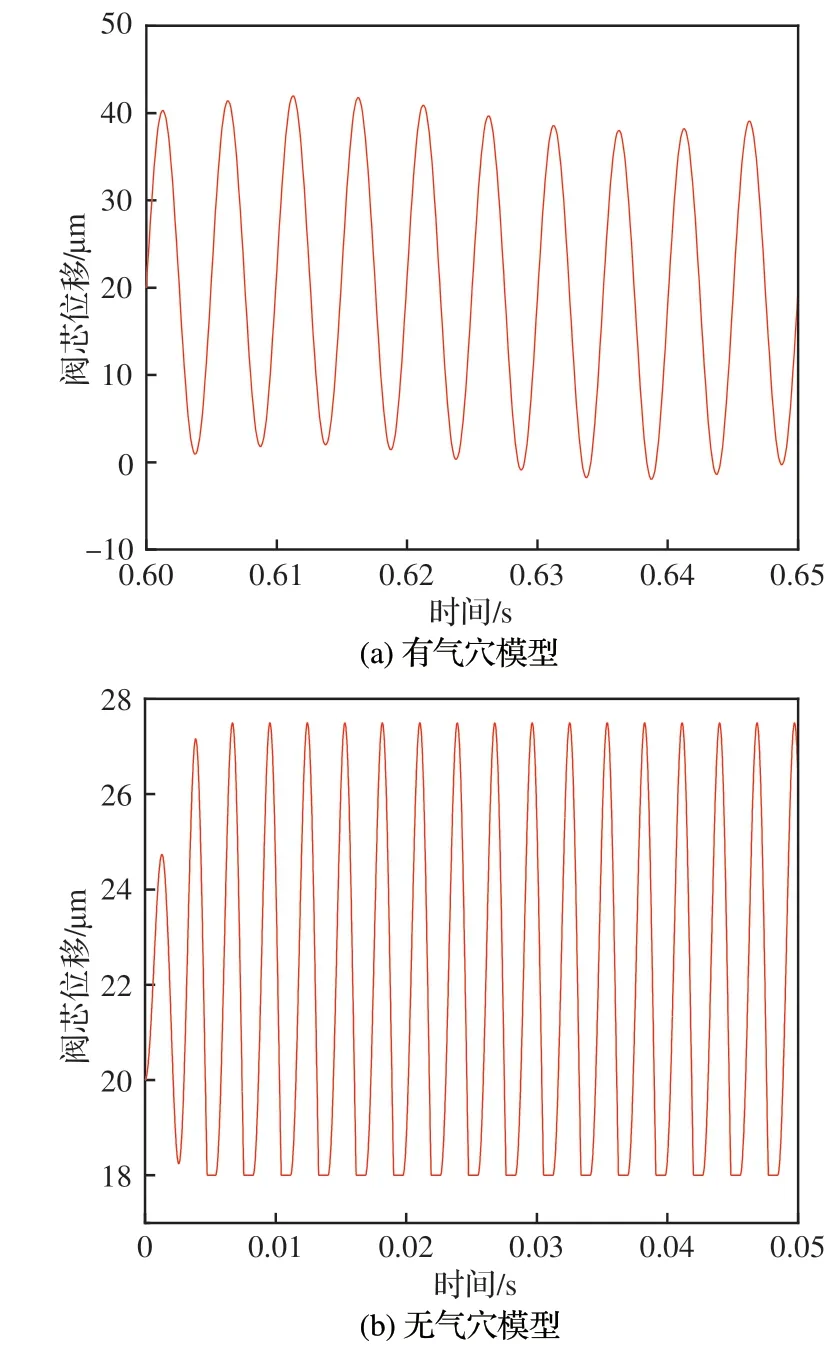
图14 阀芯位移振荡曲线Fig.14 Oscillation curves of spool displacement
图15 为双系统直驱伺服阀阀芯位移振荡对作动器位移响应的影响,阀芯位移振荡时作动器响应时间更长,控制指令变化前后皆存在较大稳态误差,且在调节过程中及稳定后均有振荡现象。可见双系统直驱伺服阀在出现阀芯振荡故障时,难以满足液压作动机构正常作动需求,极大影响了飞控系统性能。

图15 阀芯位移振荡对作动器位移响应的影响Fig.15 Effect of spool displacement oscillation on displacement response of actuator
该直驱阀用作飞机舵面作动机构时,负载变化引起作动器中工作腔油压即阀出口压力相应变化,这对阀口节流及附近凸肩面气穴有直接影响,故以出口压力表征舵面作动机构的不同负载。图16 为不同进口压力与舵面负载时的阀芯位移振荡幅值,阀芯位移振荡幅值随进口压力降低而减缓。出口压力接近于回油压力或油箱压力,节流阀口压差小,阀腔近端或凸肩面上气穴难以形成或气穴区域小,阀腔内压力脉动较低,阀芯振荡幅值相应较小。负载力大即出口压力高时,阀口压差小,气穴作用下的阀芯振荡减弱,表明舵面操控机构负载力大有利于该阀稳定工作。
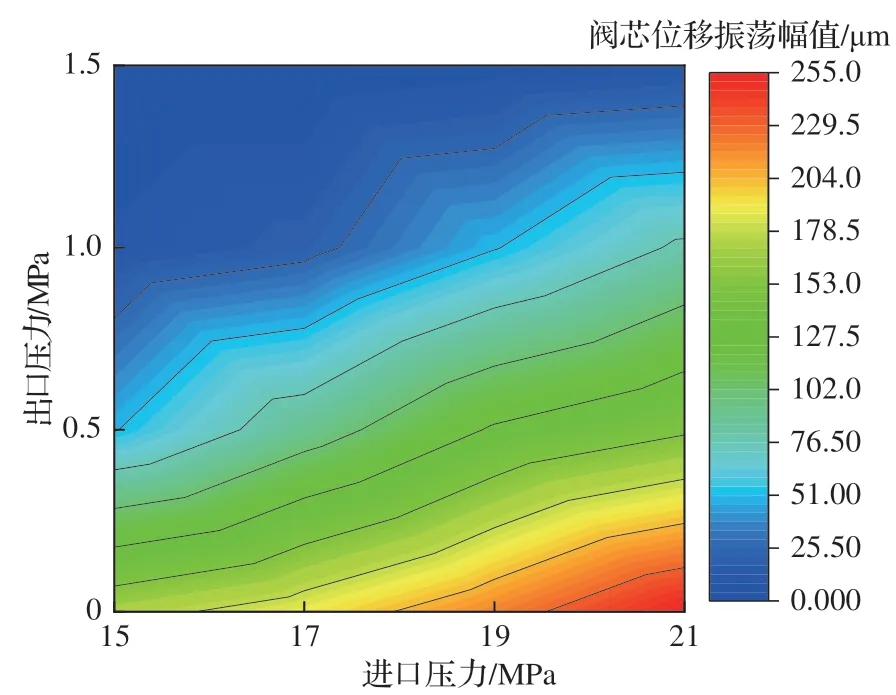
图16 不同进口压力与舵面负载时的阀芯位移振荡幅值Fig.16 Spool displacement oscillation amplitude for different inlet pressure and rudder surface load
为了获得设计参数对空化及其附着力的影响特性,根据阀口气穴进入阀腔的空泡形成变化情况提出了具体方案,研究分析其有效性。
图17(a)为不同长径比时的阀芯位移振荡曲线,长径比较小即阀腔容积较小时,阀芯位移振荡幅值也相应减小。初始方案长径比为0.67,阀芯振荡幅值在20~30 μm 之间;长径比仅降低18%,振荡幅值可降至10 μm 左右,约为初始方案的30%。然而,阀芯振荡频率在180~200 Hz 之间,表明长径比对其影响较小。除长径比是影响振荡幅值的重要因素外,该直驱伺服阀为满足阀口设计要求而采用的两级节流阀套通流结构,也与阀腔内气穴程度有直接关系。为此,研究了阀口前节流通道级数的影响。图17(b)给出了三级节流与两级节流阀芯位移振荡特性的对比。采用三级节流孔结构时,阀芯振荡幅值降低至两级节流时的30%左右。以上算例表明,阀腔及阀口设计参数对阀腔气穴发生及气穴程度有较大影响。通过仿真获得最佳设计参数可抑制因气穴而诱发的阀芯凸肩面上的压力振荡,从而达到抑制阀芯振荡的效果。
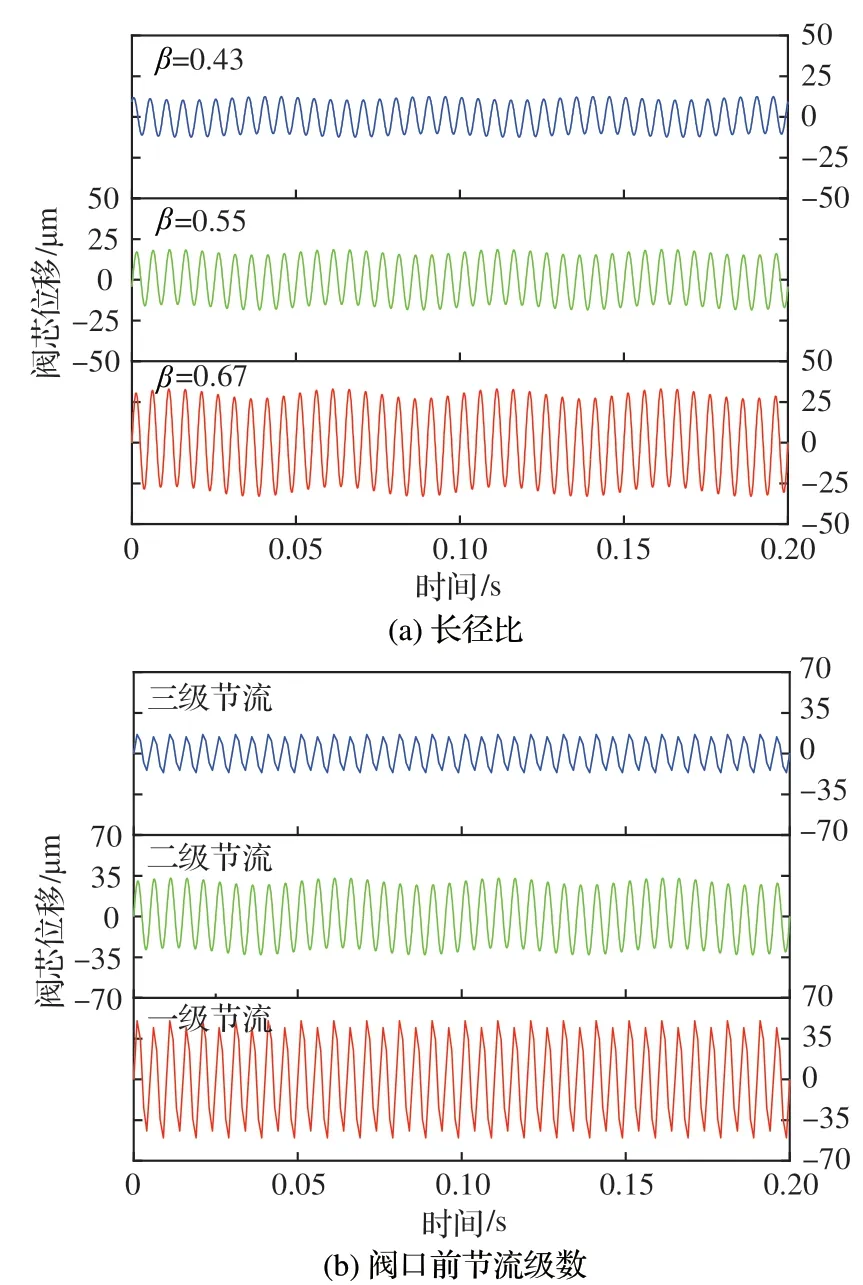
图17 结构参数对阀芯位移振荡的影响Fig.17 Influence of structure parameter on spool displacement oscillation
基于阀芯动力学仿真及数值模拟,对不同关键参数的阀芯振荡进行权重拟合分析,获得阀芯长径比β与振荡幅值关系为
式中:pa和pb分别为与阀进出口压差和输出流量相关的修正系数。计算后pa=0.231,pb=3.51,基于仿真数据测试其置信度达95%。
4 验证实验
为验证本文方法的可靠性,进行了该双系统直驱伺服阀供油特性实验,实验系统原理如图18(a)所示。系统主要包含油源、被试双系统直驱阀、力矩电机、位移传感器、示波器和流量计等。图18(b)为双系统直驱伺服阀及测试系统,图18(c)为被试阀阀芯样件。实验中,基于伺服阀空载流量特性测试方法对被试阀进行实验,供油压力21 MPa。实验依照该阀机载典型工况设计,相关工况均从实际飞控系统解析获得。控制器对被试阀发送指令,将阀芯稳定至测试开度(如0.2 mm)。力矩电机和位移传感器分别安装至被试阀阀芯两端,力矩电机用于测量阀芯所受合力,位移传感器测量阀芯位移即阀口开度(精度为微米级)。力矩电机可在低速甚至堵转(即转子无法转动)时仍能持续运转且不损坏。在此工作模式下,电机可提供给负载稳定的力矩,力矩电机轴不以恒功率而以恒力矩输出动力。测量流体力时,通过力臂杆连接阀芯末端和力矩电机,阀体中的直驱电机将阀芯驱动至指定位置后停止输入推力,调整力矩电机输出力矩大小,使阀芯保持在原位置,阀芯位置稳定后通过力矩电机的输出力矩即可计算出此时阀芯所受流体力。实验采用直流稀土力矩电机,其输出力矩与电流成正比,需提前标定,测量误差不大于1%。

图18 实验系统Fig.18 Experimental system
因改变阀口前节流通道级数对阀套厚度及加工提出了更为苛刻的要求,在现有阀总体结构重量限制下难以实现。实验仅测试了2 种回油腔阀杆长径比的阀芯位移振荡,分级节流结构抑制气穴发生以减弱阀芯振荡的优化方案未进行实验。实验中,降低阀杆长径比未引起整阀压降等关键参数变化。
图19 为阀芯所受液动力和气泡附着力在不同开度下的仿真结果,液动力呈不断增大的趋势,这是由于阀口开启过程中流量不断增大。而气泡附着力先增大后减小,这是由于在阀口逐渐打开过程中,随开度增大阀口对油液的节流作用逐渐减弱,气穴程度随之减轻。而在开启初期,虽然因阀口大压降的节流产生严重气穴,但此时油液流量较小,气泡数量也较少。随开度增加,流量增加,气泡附着力也相应增加。气泡附着力的上升段主要受流量影响,下降段主要受气穴程度影响。因此总流体阻力在开启过程中也呈现先增加后减小的趋势。
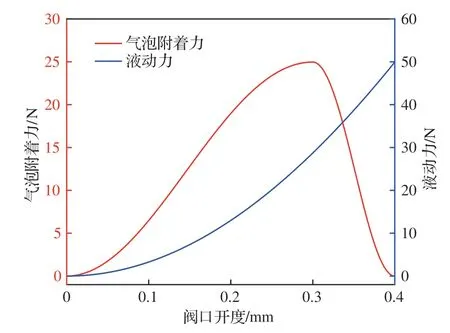
图19 阀芯气泡附着力和液动力仿真结果Fig.19 Simulation result of bubble adhesion force and flow force on spool
图20为不同长径比的两套被试阀阀芯所受总流体阻力测试结果。图20(a)将实验数据与仿真结果进行了对比,总流体阻力变化趋势基本相同,但在阀口全开时,实验数据比仿真结果小,可能由于实验中阀口全开时,流经阀口前后的油液压差降低导致液动力数值减小。另外,长径比0.55 时,总的阀芯轴向阻力约为长径比0.67 时的60%,两阀芯所受轴向流体阻力随开度变化趋势基本一致。
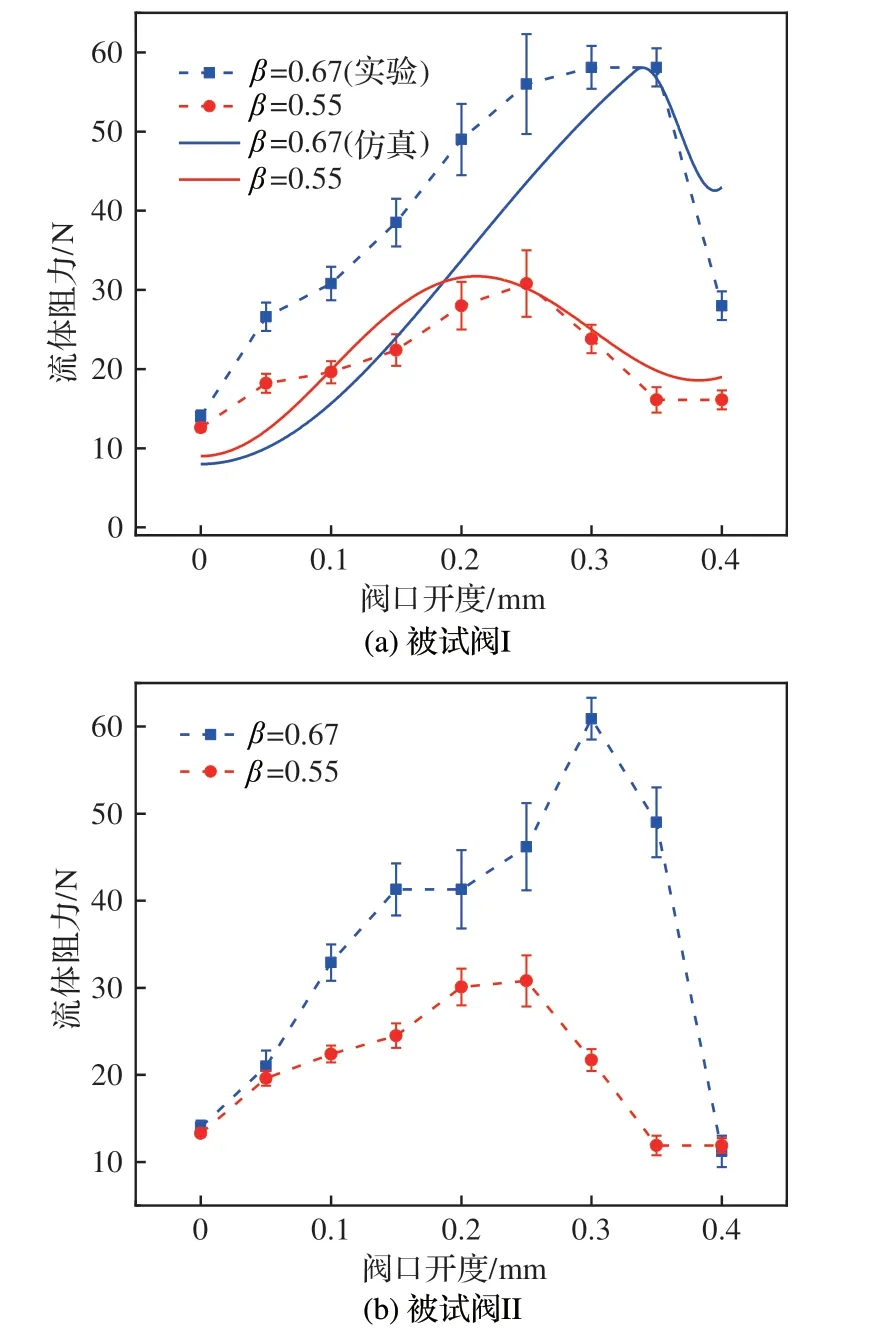
图20 阀芯上总流体阻力测试结果Fig.20 Test result of total fluid resistance on spool
图21为不同回油腔阀杆长径比时的阀芯位移振荡实验曲线,小长径比的阀芯振荡幅值得以显著抑制。长径比为0.55 时其振荡幅值仅为10 μm 左右,与仿真结果吻合。该阀实验系统泵源供油压力(含脉动水平)测试过程中不变,而实验显示,阀芯振荡仅发生于阀芯特定开口量时。另外,泵源压力脉动频率与阀芯振荡频率差异较大。实验中提高双系统直驱伺服阀背压至2.5 MPa 时,阀芯振荡与啸叫现象消失。分析得出,提高背压可使阀腔内油液压力远高于其饱和蒸气压而抑制空化,也表明系统泵源的压力脉动对阀芯振荡的影响较小,空化引起的阀腔内油压波动是造成并影响阀芯振荡的主要因素。上述内容与总液体阻力实验结果证明了通过减小回油腔容积及长径比可有效抑制由空化引起的阀芯振荡。
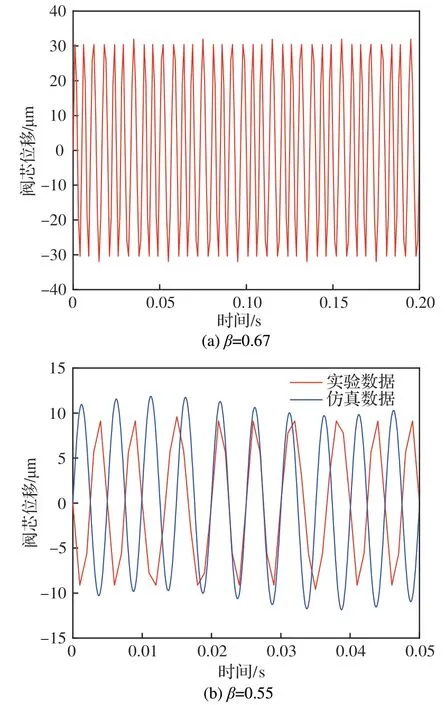
图21 不同长径比阀芯位移振荡实验曲线Fig.21 Experimental curves of spool displacement oscillation for different length-diameter ratios
5 结 论
1)阀口射流速度梯度大时空化程度高,形成的气泡附着于阀芯凸肩面,且随射流周期性分离扩散。
2)空化对阀腔凸肩面产生的脉动附着力是加剧双系统直驱阀阀芯振荡的主要因素之一,空化分离时尤为显著。
3)改进阀杆长径比或采用多级节流阀口可有效抑制阀芯振荡。减小18%回油阀腔阀杆长径比可使阀芯振荡幅值削减约67%,阀口前增加一级节流结构或渐缩形阀口可防止空化从而抑制阀芯振荡。
阀口空化诱发的直驱阀阀芯振荡,除与阀口构型和工况直接相关,还与驱动、介质及环境等因素有关。多物理场耦合建模仿真是探究阀芯振荡特性的有效手段之一,也可为直驱伺服阀性能预测、故障机理研究及优化提供一定的理论参考。

