一种改进的自适应网格划分的分布式聚类算法

蔡 莉,王浩宇,周 君,何 婧,刘俊晖

(云南大学 软件学院,昆明 650091) E-mail：caili@ynu.edu.cn

1 引 言

聚类作为数据挖掘中的一个重要功能,广泛应用于数据分析、图像处理、用户画像等多个领域.聚类算法有多种分类,有基于划分思想,比如K-means、K-medoids等,利用类内的点足够近,类间的点足够远的原则进行聚类,但其需要事先指定簇数,对于海量数据而言,准确的簇数往往难以确定[1].有基于密度思想,比如DBSCAN (Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise)、OPTICS (Ordering Points To Identify Clustering Structure)等,这类算法根据密度和最大半径进行聚类,但其存在大量的距离计算并且对于参数的依赖性很大的问题[2,3].有基于网格思想,比如STING (Statistical Information Grid)、CLIQUE (CLustering In QUEst)等,它们将数据空间划分为网格单元,把数据对象集映射至网格单元中,并计算每个单元的密度.相比于前二者,这类算法虽然在处理数据的速度上有所提升,但准确率又不能很好地保证[4].

Rodriguez和Laio提出了一种基于快速搜索和发现密度峰值的聚类算法(Clustering By Fast Search And Find Of Density Peaks),简称为DPC[5].DPC算法能够自动识别簇中心并且适用于任何形状的数据聚类,但是,对于各簇间密集程度差异较大的情况,并不能展现出很好的聚类效果.Xie等人于2016年提出一种基于DPC的改进算法FKNN-DPC (Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors)[6],其在DPC算法的基础上,运用K近邻思想,结合模糊权重进行数据点的再度分配,这种算法在大部分数据集上的效果是优于DPC的,但却增加了计算量,影响了运行效率.

单机版的聚类算法在计算性能和内存方面存在着难以解决的上限问题,很难满足对海量数据的聚类需求,而分布式计算平台则为处理海量数据的聚类提供了一种有效的途径.现有的分布式聚类算法,比如分布式K-means、分布式DBSCAN等,在处理海量高维数据时,因为其本身实现涉及大量的高维距离计算,造成了大量的计算开销,所以很大程度上也会降低分布式算法的运行效率[7,8].

为了弥补上述聚类算法的不足,本文提出了一种改进的自适应网格划分的分布式聚类算法AMCBS (An Adaptive Meshing Clustering Algorithm Based On Spark Platform).该算法能够根据数据分布自适应地划分网格以获得更好的聚类效果;同时,使用线性判别分析法处理高维数据,提高了聚类的准确性和适用性.

2 相关工作

如何高效地划分数据、合并局部簇一直是聚类算法的研究重点.汪晶等人利用样本方差和最小方差的概念,提出了一种基于最小方差来获取K-means聚类中心的分布式算法MVC-Kmeans[9],提升了原有K-means的准确率和运行效率.但算法参数的选取具有不确定性,其结果也易受参数的影响.宁建飞实现了DBSCAN聚类算法在Spark处理平台上的应用[10],提高了DBSCAN算法处理海量数据的能力.然而,算法本身存在着大量的距离和密度计算,平均耗时较长.何仝等人基于密度峰值的高效分布式聚类算法EDDPC[11],根据局部敏感哈希对数据集进行划分,并采用多次Hash方法修正分区后的结果,保证了聚类质量.但是,此算法涉及多个索引空间以及多次哈希表查询,生成的索引文件的大小是原始数据大小的数十倍甚至数百倍.He等人提出的MR-DBSCAN算法[12]采用定长网格来划分数据,将数据点集转移到了数据网格集,减少了原有计算量.不过,MR-DBSCAN算法也存在明显的缺点：一是均匀划分网格时,网格单元的大小实际难以确定,聚类效果易受网格单元大小的影响;二是算法在合并局部簇时采用增量的方式,计算效率仍然较低.Song等人和Huang等人分别提出了基于Hadoop平台下的H-DBSCAN算法[13]和基于Spark平台下的S-DBSCAN算法[14],通过分布式计算框架和加入网格边界的扩展,来提高聚类结果的精确度和局部簇的合并效率.两种算法都采用均分网格的方法来划分数据,这会导致最终的聚类结果会存在较大的误差;其次,两种算法也未充分考虑高维数据集的处理情况.

上述算法虽然在一定程度上提升了运行效率和准确度,但依旧存在诸多问题：例如在处理高维数据,性能会大大降低,聚类效果不理想;算法易受参数的影响,整体稳定性较低.

3 AMCBS聚类算法原理

3.1 相对熵

相对熵是评判两个概率分布间差异的非对称性度量单位,可以较为直观地反映数据点分布趋近于均匀分布的情况.当数据分布越趋于均匀,相对熵值越大;当数据分布越趋于集中,相对熵值越小.本文利用相对熵的这一性质,用来区分网格区间的稠密程度,从而达到自适应划分网格的目的.

定义1.在网格空间中,第i维上的单个网格的相对熵定义为：

(1)

其中,gij是第i维上的第j个网格,s(gij)是该网格里的数据数量占整个数据空间数据集的比例,Ni是第i维上的网格的数量.

定义2.在网格空间中,第i维上的全部网格的相对熵定义为：

(2)

其中,Gi是第i维上全部网格的集合.

定义3.合并网格的相对熵阈值T定义为：

(3)

其中,e(gij)是第i维的第j个网格的相对熵,Mi是第i维网格的相对熵中位数.

AMCBS算法利用相对熵自适应划分网格的过程如下：

Step1.设置初始网格长度gL,根据步长等分数据集Bi,构造网格空间中的第i维网格集合Gi;

Step2.根据公式计算第i维上的单个网格的相对熵eij;

Step3.计算第i维上的全部网格相对熵Ei以及相对熵阈值T;

Step4.遍历网格空间第i维上所有的单个网格相对熵eij,根据相对熵阈值T,进行合并操作;

Step5.重复以上步骤,直至多维网格划分完成为止.

3.2 决策图

基于决策图的聚类算法可以实现数据对象的快速聚类,核心思想是对聚类中心或密度峰值点进行相关的理论假设[15]：1)每个数据聚类簇组中的聚类中心拥有最大的局部密度参数值;2)不同数据聚类簇组的聚类中心之间有着比较远的距离.决策图聚类算法引入了两个重要的参数变量,局部密度以及数据对象到最近大密度点的距离.

定义4.每一个网格gridi的密度dsi定义为：

dsi=countNum(gridi)

(4)

定义5.每一个网格gridi到更高密度网格对象gridj的最近距离作为网格对象的距离值dti定义为：

(5)

其中,dij为网格对象gridi中心位置到网格对象gridj中心位置的欧式距离.

假设网格集合中密度最高的网格对象为mx,其距离值为dtmx：

dtmx=max(dmx,j)

(6)

AMCBS算法会计算出每个网格单元的密度dsi与距离dti,依据位于簇心位置的网格对象会同时具有较高的密度ds和较大距离dt的特点,确定网格集合中簇的个数m以及簇中心的网格单元.

3.3 线性判别分析

线性判别分析(Linear Discriminant Analysis,LDA)的原理是通过正交变换,将一组可能存在相关性的变量进行降维处理,目标是将高维数据投影至低维后,同类的数据之间距离尽可能近、不同类数据之间距离尽可能远[16].具体流程为：

Step1.计算类内均值mi与类间均值m,类内均值定义为：

(7)

类间均值定义为：

(8)

其中,mi和m均为k维向量;

Step2.计算类间散度矩阵Mb与类内散度矩阵Mw,类间散度矩阵定义为：

(9)

类内散度矩阵为：

(10)

类间散度矩阵Mb与类内散度矩阵Mw均为k阶方阵;

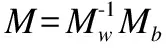
Step4.对初始的特征值进行线性变换,选取前i个特征向量,组成投影矩阵：

W=[v1,…,vi]

(11)

则经过降维后的新样本为：

[Y1,…,Yk]=WT[X1,…,Xk]

(12)

AMCBS在处理高维数据时,会通过LDA的方式将其统一转化为低维数据(一般是二维或者三维),之后把转化后的低维数据输入进Spark应用程序中,执行对应的处理单元.

3.4 Spark平台

Spark是加州大学伯克利分校AMP (Algorithms,Machines,and People Lab)实验室开发的一个基于内存计算的大数据并行计算框架.与MapReduce相比,Spark在处理大规模数据时,具有更高的效率,其主要原因是：一是把Job的中间结果直接存放至内存中,可以更好的适用于机器学习以及数据挖掘的多次迭代计算;二是引入了弹性分布式数据集(Resilient Distributed Dataset,RDD),其本质上是分布在一组节点中的只读对象集合,具备像MapReduce等数据流模型的容错特性,可以允许进行重建操作;三是更加的通用,提供了多种数据集的操作类型;四是支持用户自主确定分区策略,可以做到尽量少的在不同的执行单元之间使用网络交换数据,减少运行时间[17,18].本文利用Spark平台完成数据预处理、网格划分、剩余点分配等操作,提升了算法的运行效率,流程框架如图1所示.

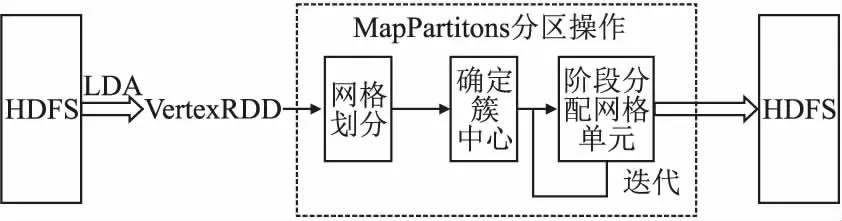
图1 AMCBS分布式算法的框架Fig.1 AMCBS distributed algorithm framework

AMCBS分布式算法主要处理步骤如下：

1)创建Spark对象,SparkContext的创建是运行Spark程序必要的开端.

2)从分布式文件存储系统HDFS中读取经过LDA降维后的低维数据集,并将其转化为RDD格式.

3)计算出数据集各维度的边界值,执行网格划分函数,根据相对熵及其阈值,获得多维自适应网格集,并将结果广播至各个分区Partition.

4)计算每个网格单元最近的K个单位,采用SparkRDD的mapPartitions方法将函数作用到每个分区.

5)计算网格聚类中心,采用reduceByKey函数,分别计算同一簇下的样本对象和sum和样本数量count.

6)执行不同方式的单元分配函数,并进行迭代,直至符合分配标准为止.

7)迭代结束后,返回聚类结果集Cluster,算法结束.

4 AMCBS算法描述

AMCBS算法中所涉及到的变量定义如表1所示.

表1 AMCBS算法中的变量定义Table 1 Notations in AMCBS algorithm

AMCBS算法的伪代码描述如表2所示.

表2 AMCBS算法伪代码Table 2 Pseudocode of AMCBS algorithm

5 实 验

本文的实验环境是由3台Linux Ubuntu 16.04操作系统的高性能服务器搭建出一个Spark分布式集群,其中包含一台管理服务器(master)以及两台工作服务器(slave).集群中每个节点具体配置为CPU Intel i7-9800X,内存60GB,硬盘4TB.

5.1 实验数据集

实验数据集包括UCI机器学习标准数据集、奥利维蒂人脸数据集、GitHub文本数据集和D31数据集.各数据集的数据量、数据维度和类别数如表3所示.

表3 实验数据集相关特征Table 3 Correlation characteristics of experimental data sets

为了验证AMCBS算法的有效性,将该算法的聚类结果与分布式FKNN-DPC算法、EDDPC算法、分布式DBSCAN算法和基于网格聚类的S-DBSCAN算法进行对比.采用常用的评价指标准确率(Accuracy,ACC)、调整互信息(Adjusted Mutual Information,AMI)、调整兰德指数(Adjusted Rand Index,ARI)和同质性(Homogeneity)等来衡量5种算法的聚类性能.其中,ACC是指正确聚类数据量占总体数据量的比例;AMI是基于互信息分数来衡量结果簇向量与真实簇向量相似度,AMI取值越大说明簇向量的相似度越高,AMI越接近于0则表示簇向量越是随机分配;ARI是衡量两个数据分布之间的吻合程度,取值范围在[-1,1],值越大,表示聚类结果和真实情况越吻合;Homogeneity是指每个簇中正确分类的样本数占该簇总样本数的比例和.

5.2 实验结果分析

5.2.1 UCI数据集对比实验

UCI数据集包含了Iris数据集(4维)、Seeds数据集(7维)、Wine数据集(13维)和Libras movement数据集(90维),各算法在4个评价指标上的对比结果如图2～图5所示.可以发现：AMCBS算法在Iris数据集、Seeds数据集和Wine数据集上的评价结果均优于其他算法,对于Libras movement数据集而言,AMCBS算法的ACC和Homogeneity指标也是最好的.

5.2.2 奥利维蒂人脸数据集

奥利维蒂人脸数据集是机器学习领域常用的一个标准数据集,40个志愿者提供了不同角度、不同表情的各10张面部图片组成,共计400张.本文将每张人脸图片转换成向量(46×56),经过数据压缩后作为输入数据,并进行聚类.这里,以前100张和全部的400张图片作为数据集分别实验,以验证AMCBS算法的有效性.前100张图片的具体实验结果如图6所示.

图2 Iris数据集结果 Fig.2 Iris data set results图3 Seeds数据集结果 Fig.3 Seeds data set results图4 Wine数据集结果 Fig.4 Wine data set results

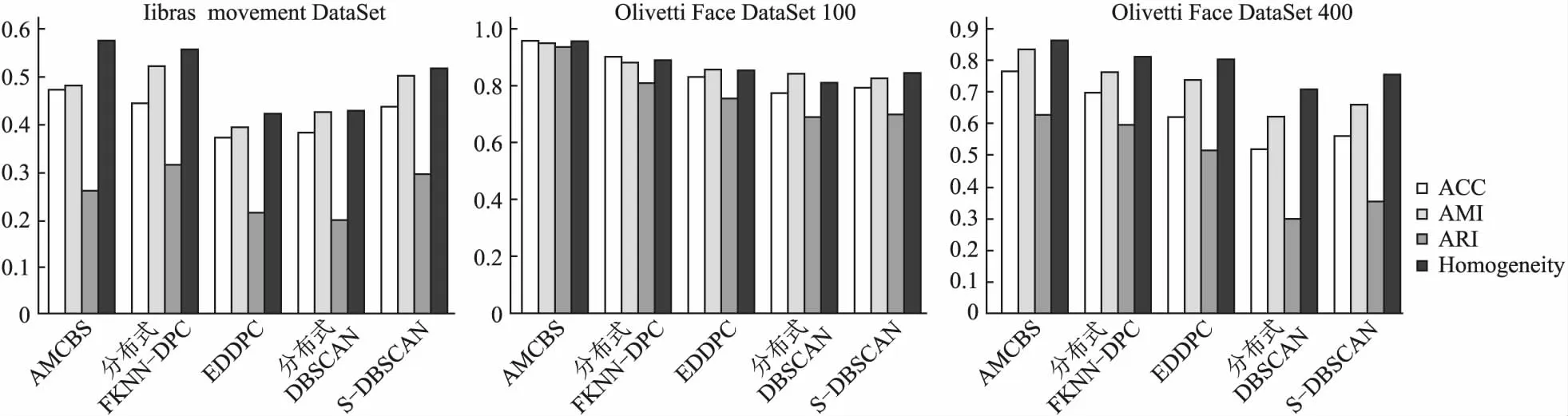
图5 Libras数据集结果 Fig.5 Libras data set results图6 人脸数据集前100张图片结果 Fig.6 Results of the first 100 images in the face data set图7 400张图片结果 Fig.7 400 picture results

400张图片具体实验结果如图7和图8所示.由图6～图8可知：无论是前100张还是整个400张人脸图片,AMCBS在评价指标和运行时间上都优于对比算法.

图8 400张图片运行时间 Fig.8 Running time for 400 images图9 GitHub数据集结果 Fig.9 GitHub sets results图10 GitHub运行时间 Fig.10 GitHub running time

5.2.3 GitHub文本数据集

GitHub文本数据集是由3个类别的中文文本标签所组成,包括8000个动物标签、8000个食品标签和8000个药物标签,共计24000个.本文在处理中文标签时,采用了BERT模型,把词转换成向量(768维),作为输入数据并进行聚类,具体实验结果如图9和图10所示.可以发现：AMCBS算法对于处理较大规模文本数据集也有较好效果,在ACC、AMI和Homogeneity指标上均优于其他4种算法,运行时间上也有明显优势.

5.2.4 D31数据集

D31数据集包含了3100条2维数据,共有31个类别,每个类别100条数据,因该数据集本身就是2维数据,所以就没有通过LDA降维,而是直接作为输入数据进行聚类,其实验结果如图11所示.可以看出：AMCBS算法在ACC、AMI、Homogeneity和运行时间上均优于其他4个算法,并且ARI也处于较高水平.

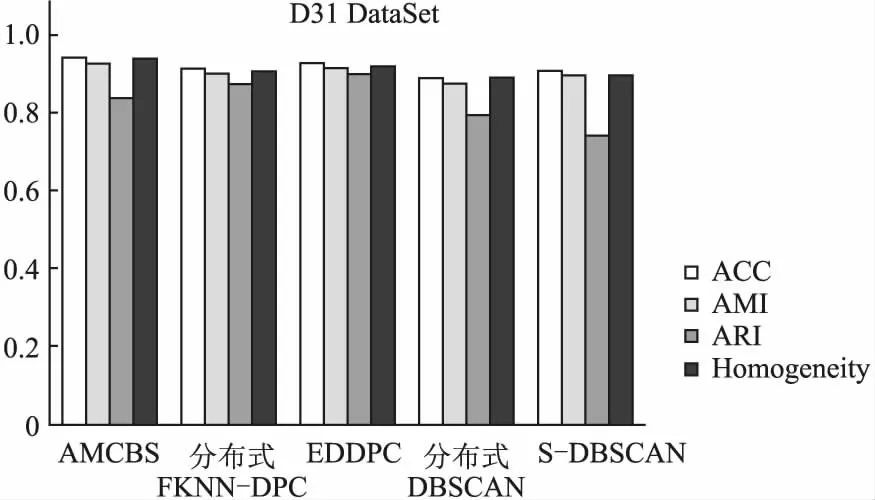
图11 D31数据集结果Fig.11 Results of D31 data set

为了进一步地说明算法对于大规模数据集的适应性,本文扩充了D31数据集,之后,分别选取3.1×104、3.1×105、3.1×106和3.1×107数量级的数据进行实验,其结果如图12所示.可以看出：随着数据集的逐步增大,AMCBS算法与其他4种分布式算法相比,运行时间大幅减少,效率提升明显.

6 结束语

为了解决现有算法在运行时间和正确率上存在的问题,本文提出了一种改进的高效分布式聚类算法,通过分布式技术和自适应网格划分的思想来处理高维海量数据.其主要工作有：1)根据数据点在空间的分布状况,利用相对熵进行自适应网格划分;2)利用决策图的思想,根据各单元距离密度值,确定网格集合中的各个簇;3)引入了线性判别分析,对于高维数据,通过降维手段,进行预处理;4)为了提高算法的聚类准确度,采用了阶段式分配策略;5)结合Spark计算平台,使用并行化合并局部簇,从而进一步提升网格聚类算法的并行化效率.通过与4种分布式算法在UCI数据集、人脸图片数据集和文本数据集等进行对比,可知AMCBS算法对于海量数据和高维数据均具有较好的有效性和处理性能.不过,在剩余点的分配过程中,网格辐射范围的选取会在一定程度上影响聚类结果,目前的解决办法是多次实验以获得最好的效果;此外,本文没有解决在不平衡数据融合下的聚类问题,这两点将是论文下一步的研究重点.

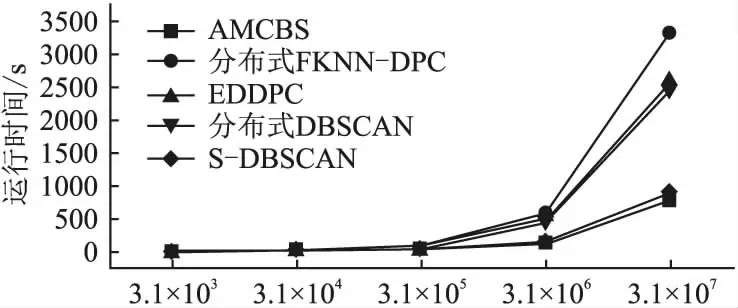
图12 各算法在扩充数据集上的运行时间Fig.12 Running time under the extended data sets