基于计算思维的初中信息技术项目式活动设计与实施
罗训炉

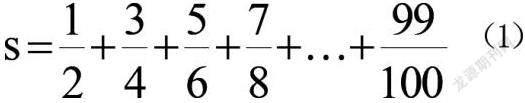





摘要:本文以“设计算法实现用数学公式计算”项目为例,探究如何借助项目式学习在初中信息技术课堂中培养学生的计算思维能力,以期学生能够利用计算思维解决学习和生活中存在的问题。
关键词:信息技术;计算思维;初中学生;程序设计
中图分类号:G434 文献标识码:A 论文编号:1674-2117(2023)08-0044-03
《义务教育信息科技课程标准(2022年版)》(以下简称“新课标”)将利用计算思维分析解决学习、生活中的问题作为课程的一个主要目标,提出让学生学会应用计算思维的方法分析问题,对具体问题进行抽象和建模,提出解决问题的方案,并在数字化学习与生活的情境中开展真实性学习。项目式学习则是以研究学科概念、原理为中心,以解决真实的问题为目的,在真实情境中借助多种资源解决问题的一种学习模式。在这种新型的学习方式中,学生更容易接受学习,获得更加有效的学习效果。
现阶段初中开设程序设计课存在的问题
在新课标发布前,初中信息技术课程没有统一的课程标准,没有统一的教材,各地市主要依据《中小学综合实践活动课程指导纲要》中“设计制作活动(信息技术)”推荐的学习主题组织教学,教学目标旨在鼓励学生动手操作,将自己的创意、方案付诸现实,转化为物品或作品。指导纲要注重提高学生的技术意识、工程思维、动手操作能力等。各地市在实际操作中一般是根据本地区的实际情况组织教师编写地方教材,课程内容以各类应用软件的操作为主,部分地区开设了Visual Basic、C语言、Python等编程课程。在开设程序设计的地区,课程一般以程序语言的介绍和训练为主,教学模式相对陈旧,教材编排、课程设计和教学模式大量借鉴高中甚至大学阶段的程序设计专业课,过于注重概念、语法、结构的介绍,学生把大量时间花在语句功能和用法等知识的学习上,造成学生学习浮于表面,不符合计算思维核心素养的培养路径。
下面,笔者基于上述问题,以项目式活动“设计算法实现用数学公式计算”对圆周率π的计算为例,谈谈如何利用程序设计培养初中学生的计算思维能力。
基于计算思维的项目式活动设计与实施
1.活动目标的规划与设定
Python语言是近年来较为流行的编程语言之一,许多地区将Python语言作为初中阶段程序设计的首选入门语言。在前序课程中,学生对Python语言的基础知识和基本编程方法有了初步了解,已经能动手编写一些简单应用程序。
本项目活动的教学目标是通过探究不同算法对圆周率计算的影响,了解应用循环结构解决具体问题的方法,提升学生计算思维的深度和广度。“设计算法实现用数学公式计算”项目旨在根据学科核心素养,提升学生的计算思维能力。同时,笔者根据学生的实际情况,对现有教材内容进行了设计与重组。
2.知识的储备与学习
活动一:计算1~10的奇数和。
在实际教学中,学生根据已有知识,利用等差数列求和公式轻松完成任务。于是,教师进一步提出问题:能否用同样的方法计算1+1/2+1/3+1/4+… +1/999的和?学生会发现,这个问题没有现成的公式,用print(1+1/2+1/3+1/4+…+1/999)来计算又特别烦琐。如何解决这个问题呢?这时教师可以引导学生回忆传统纸笔计算此类问题的方法,并提出累加和的概念,引入本次活动的学习内容(如图1)。
在上例中,学生遇到了还没学到的for语句和range函数,教师可以让学生先通过单词的字面意思猜測程序的功能和执行过程,初步感受for循环的作用与功能。学生运行图1所示的程序代码,可快速得到答案,进而体验探究成功的乐趣。
活动二:探究for循环语句的格式与功能。
对初学者来说,程序设计有两道坎:一个是循环,另一个是递归。因不少学生一开始没能很好地理解循环结构的精髓,所以后续的课程变得相对困难。因此,要让学生深刻理解什么是循环、什么是循环控制变量,了解循环变量初值、终值和步长值的设定方法,学会构造循环体,让看似无规律的数据变换成有规律的数据,使循环能不断重复执行下去。
for循环包括for、in关键字和rang函数等,在上例中,学生根据教师提供的教学资源包,可以很快弄清for循环结构的功能是重复执行循环体中的程序块多次,直到rang范围中的每个值枚举完毕,退出循环。另外,在上例for循环中,i是循环变量,初值为1,变化范围为1≤i<1000,循环的步长值为1。for语句的后面要紧跟一个冒号“:”,表示后面是一个程序段,是循环体部分。循环体中的程序段要采用缩进格式,且要有相同的缩进量。对于循环变量i的终值为什么是999而不是1000,此时教师应发挥主导作用进行分析和解释。
3.计算思维能力的训练与培养
经过上述活动的学习和探究,学生对for循环的结构、功能和实现的过程有了初步的了解,接下来就可以通过对一些有规律问题的探究,进一步加深理解循环结构的使用方法,解决更多现实生活中存在的问题,训练和培养学生的计算思维。
活动三:分别用for循环计算下列式子的值。
通过观察可以得出,算式(1)中每一项的组成都是有规律的:分子从1变化到99,每次递增2,分母的变化规律是从2变化到100,每次也是递增2,且每一项分母的值都比分子多1。可以分别用i和i+1表示分子和分母的值,循环中每次递增的步长可在range函数中设定,这样就可圆满地解决上述问题(如图2)。
算式(2)看起来好像有点复杂。其实,若仔细观察,还是可以非常容易地发现其中的规律:在程序中,对于枚举的每个变量i,可以用i和i+2表示分子中的两个乘积项,用i+1和i+3表示分母中的两个乘积项,这样问题就可以得到解决,不需要设置4个控制变量(如下页图3)。在本活动中,教师还要提醒学生注意除式表达式的表示方法,否则将得到错误结果。
4.探究不同算法对圆周率计算精度的影响
早期的圆周率大都是通过实验而得到的。第一个用科学方法寻求圆周率数值的人是阿基米德,他在《圆的度量》中用圆内接和外切正多边形的周长确定圆周长的上下界,从正六边形开始,逐次加倍计算到正96边形,得到(3+(10/71)<π<(3+(1/7)),得出精确到小数点后两位的π值。南北朝著名数学家祖冲之得出精确到小数点后7位的π值,即3.1415926<π<3.1415927,他的辉煌成就比欧洲早了1000多年。本次活动教师引导学生探究不同方法对圆周率计算的影响,提升学生的计算思维能力。
活动四:分别利用不同算式计算圆周率π,比较其精度。
算法(3)简单明了(如图4),非常容易实现,大部分学生都可以轻松完成。但这个算法运算速度太慢,计算精度太差,当n取值10时,只能得到1位小数精度的圆周率,当n取值10000时,也才能得到3位精度的圆周率。算法(4)看起来稍显复杂(如图5),学生初次接触存在一定的畏难情绪,不知从何下手。此时,教师要引导学生仔细观察算式中每項的组成。通过分析不难发现,算式中的每一项的内容组成都是在前一项的基础,乘上一项新的乘积,且新乘上的值也是有规律的,可以通过增加一个新的临时变量,用于存储前一项的值,这样就可圆满解决该问题。
算法(4)的编程难度不大,但程序效率却有了惊人的提升,当n的取值为10时,可以获得3位的小数精度,当n的取值为50时,可以得到14位的小数精度。
上述两种方法可较好地解决圆周率的计算问题,但它们有个共同的缺点,就是无法准确知道当前圆周率的精度。那么,如何解决这个问题呢?接下来教师引导学生展开头脑风暴,进行小组讨论,探讨利用while循环结构控制圆周率精度的计算(如图6),圆满解决本次项目式学习的最终问题。
通过对圆周率不同算法的探究编程,学生亲历了计算思维的全过程,感受了不同算法对圆周率计算的影响,计算思维能力得到了进一步的加强和提升。计算圆周率还有许多方法,教师还可以引导学生课后进行进一步的探究与实践,加深对循环结构的理解。
在本次活动的最后,教师还可以对学有所长的学生进一步提出要求:通过实验可以发现,上述改进算法虽然能较好地控制圆周率的计算精度,但由于计算机采用浮点数的形式来存储和处理实数,不能存储和处理无限位数的小数。在Python中,一个单精度数最多只能存放15位小数,但现在计算机已经可以非常轻松地计算几万位的圆周率,这是如何做到的呢?于是,教师引导学生继续了解和探究高精度算法的概念和处理方法,让学生尝试利用数组来存放超过15位的小数,实现高精度计算,让不同层次、不同水平学生的计算思维能力都能得到提升。

