计算特定群体中杂合子比例的一个简便公式——从2022年6月浙江高考25题D项谈起

郑 晶

(浙江省金华市外国语学校)

1.真题呈现

(2022年6月浙江高考25题)下图为甲、乙两种单基因遗传病的遗传家系图,甲病由等位基因A/a控制,乙病由等位基因B/b控制,其中一种病为伴性遗传,Ⅱ5不携带致病基因。甲病在人群中的发病率为1/625。不考虑基因突变和染色体畸变。下列叙述正确的是

( )

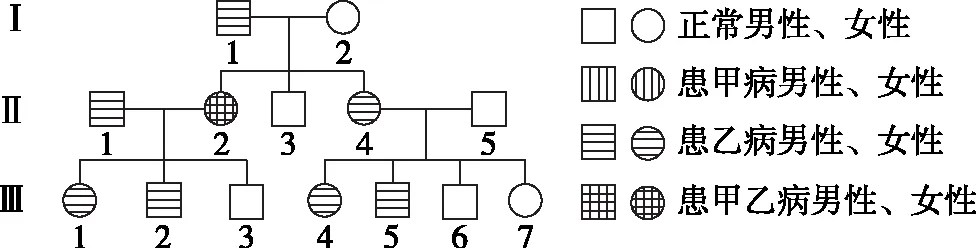
A.人群中乙病患者男性多于女性

B.Ⅰ1的体细胞中基因A最多时为4个

C.Ⅲ6带有来自Ⅰ2的甲病致病基因的概率为1/6

D.若Ⅲ1与正常男性婚配,理论上生育一个只患甲病女孩的概率为1/208

参考答案:C

D项解析:由遗传家系图结合题干“其中一种病为伴性遗传”可知甲病为常染色体隐性遗传病,乙病为伴X染色体显性遗传病。单独考虑乙病,由于Ⅲ3表型正常,可知Ⅱ2的基因型为XBXb,Ⅲ1的基因型及概率为1/2XBXB、1/2XBXb,正常男性的基因型为XbY,婚配后生育一个不患乙病的女孩(XbXb)的概率为1/2×1/4=1/8。单独考虑甲病,Ⅲ1的基因型为Aa,正常男性的基因型为AA或Aa。要想求出其中Aa的概率,需利用题干中“甲病(aa)在人群中的发病率为1/625”这一条件,根据哈迪-温伯格定律,先算出a的基因频率q=1/25(式①)、A的基因频率p=1-q=24/25(式②);再得出该群体中AA的基因型频率p2=242/625(式③)、Aa的基因型频率2pq=2×24/625(式④);最后推导出正常人(A_=AA+Aa)基因型为Aa的概率=正常人群中杂合子比例=2pq/(p2+2pq)=(2×24/625)/(242/625+2×24/625)=1/13(式⑤)。所以,Ⅲ1与正常男性婚配后生育一个患甲病的孩子(aa)的概率为1/13×1/4=1/52。综上,同时考虑甲乙两病,Ⅲ1与正常男性婚配,理论上生育一个只患甲病女孩的概率=1/8×1/52=1/416,D项错误。

从上述解析不难看出,D项的烦琐计算主要集中在由人群中a的基因频率(式①)推导正常人群中Aa比例(式⑤)的步骤,可谓既耗时又易错,部分学生因考试时间紧迫不得不放弃对该选项的解答。然而此类题型在近年浙江高考中却频繁出现,往往位于选择题压轴题中,如2017年11月28题、2019年4月28题、2020年1月25题、2022年6月25题。为破此困局,笔者对大量同类试题进行了比较分析、寻找规律,最终归纳出了一个简便公式。该式无需进行式②、式③、式④的复杂演算,可直接从式①求出式⑤。经实践证明,简便公式对提升此类问题的解题速度及正确率颇有助益。

2.公式推导

2.1简便公式1

参考上题中由a基因频率=1/25(式①)推导A_中Aa比例=1/13(式⑤)的过程,将遗传平衡群体中的a基因频率设为1/n,则A基因频率=1-1/n=(n-1)/n,AA基因型频率=(n-1)2/n2,Aa基因型频率=2(n-1)/n2,A_中Aa的比例=[2(n-1)/n2]/[(n-1)2/n2+2(n-1)/n2]=2/(n+1)。这便是简便公式1的表达式。具体到上题,将n=25带入简便公式1,即可快速求出A_中Aa的比例=2/(n+1)=2/(25+1)=2/26=1/13。

2.2简便公式2

并非所有群体的a基因频率写成分数时,分子均为1。设a基因频率的分子为m,即a基因频率=m/n,则A基因频率=1-m/n=(n-m)/n,AA基因型频率=(n-m)2/n2,Aa基因型频率=2m(n-m)/n2,A_中Aa的比例=[2m(n-m)/n2]/[(n-m)2/n2+2m(n-m)/n2]=2m/(n+m)=(m+m)/(n+m)。这便是简便公式2的表达式。事实上,简便公式1是简便公式2中m取1时的特殊结果,故下文只对简便公式2进一步分析,并称之为“简便公式”。

对于遗传平衡群体,将a的基因频率整理成分数形式m/n,然后对分子、分母分别加上分子m,使分子变成m+m,分母变成n+m,即得到A_群体中Aa的比例。

如某群体中a基因频率=7/100,则显性表型群体(A_)中杂合子(Aa)的比例=(7+7)/(100+7)=14/107。可见,简便公式省去了常规解法中繁复的中间步骤,一步即算出答案,既便捷又准确。

需要说明的是,之所以将简便公式中分子的2m描述为m+m,是为了在实际应用中将分子与分母的变化相统一,更易于记忆。

糖尿病组尿微量白蛋白阳性检出率为69.85%(397/2 000)，尿糖阳性检出率为66.30%(1 326/2 000)，联合检测阳性检出率为73.65%(1 473/2 000)，均显著高于健康对 照组的 1.60%(8/500)、1.20%(6/500)、2.20%(11/500)，差异有统计学意义（P＜0.05），见表 2。

3.公式含义

“矩形拼接法”有助于直观理解简便公式的含义。如图1甲所示,正方形BCDE边长为n,点F、G、H、K分别是位于四条边上的点,并将各边分为n-m及m两段。连接FG、HK,相交与点J,正方形BCDE被分割成四个小矩形。

边长含义:BF/BC=(n-m)/n,表示A基因频率;FC/BC=m/n,表示a基因频率。其他各边同理。

面积含义:正方形BFJH/正方形BCDE=(n-m)2/n2,表示AA基因型频率,其他各矩形同理。

当求解A_群体中Aa比例时,先将表示aa的矩形JKDG去除(图1乙),再将矩形HJGE(灰色)旋转90°,拼接至矩形FCKJ的右侧(图1丙),使边CK与边JH重合。由于这两个表示Aa的矩形大小形状完全一致,故拼接后可得到一个新的完整矩形BG′E′H。此时Aa占A_的比例=矩形FG′E′J的面积/矩形BG′E′H的面积=FG′的长度/BG′的长度=(m+m)/(n+m)(矩形的宽相同,已约去),简便公式得证。

简言之,已知的是甲图中a基因频率=FC/BC,要求的是丙图中A_中Aa的比例=FG′/BG′,两者的区别就在于分子分母同时加了一段长度为m的CG′。而实现从面积之比(基因型频率)到边长之比(基因频率)转化的,正是矩形拼接过程。由此亦可推测,凡是符合上述矩形拼接条件的,均属简便公式的适用范围。

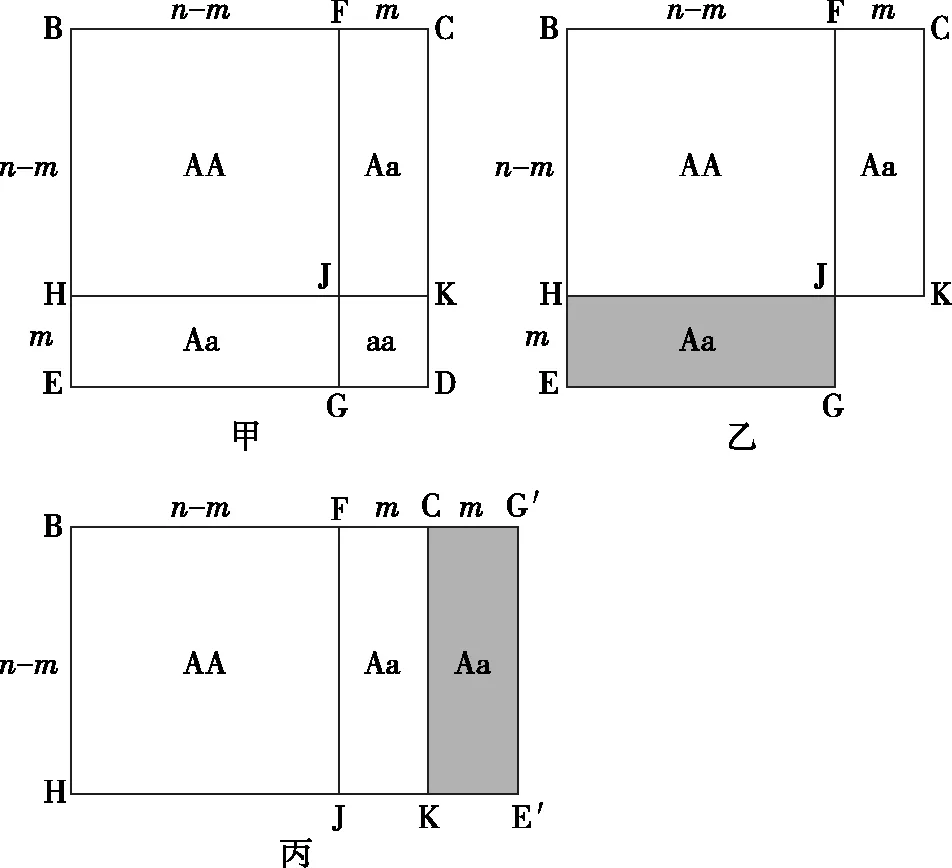
图1 矩形拼接法

4.拓展应用

除前述例题一类的情境外,简便公式是否有更广阔的应用范围呢?

4.1随机交配并淘汰某种纯合子

4.1.1淘汰aa

常规解法:求解过程见表1。

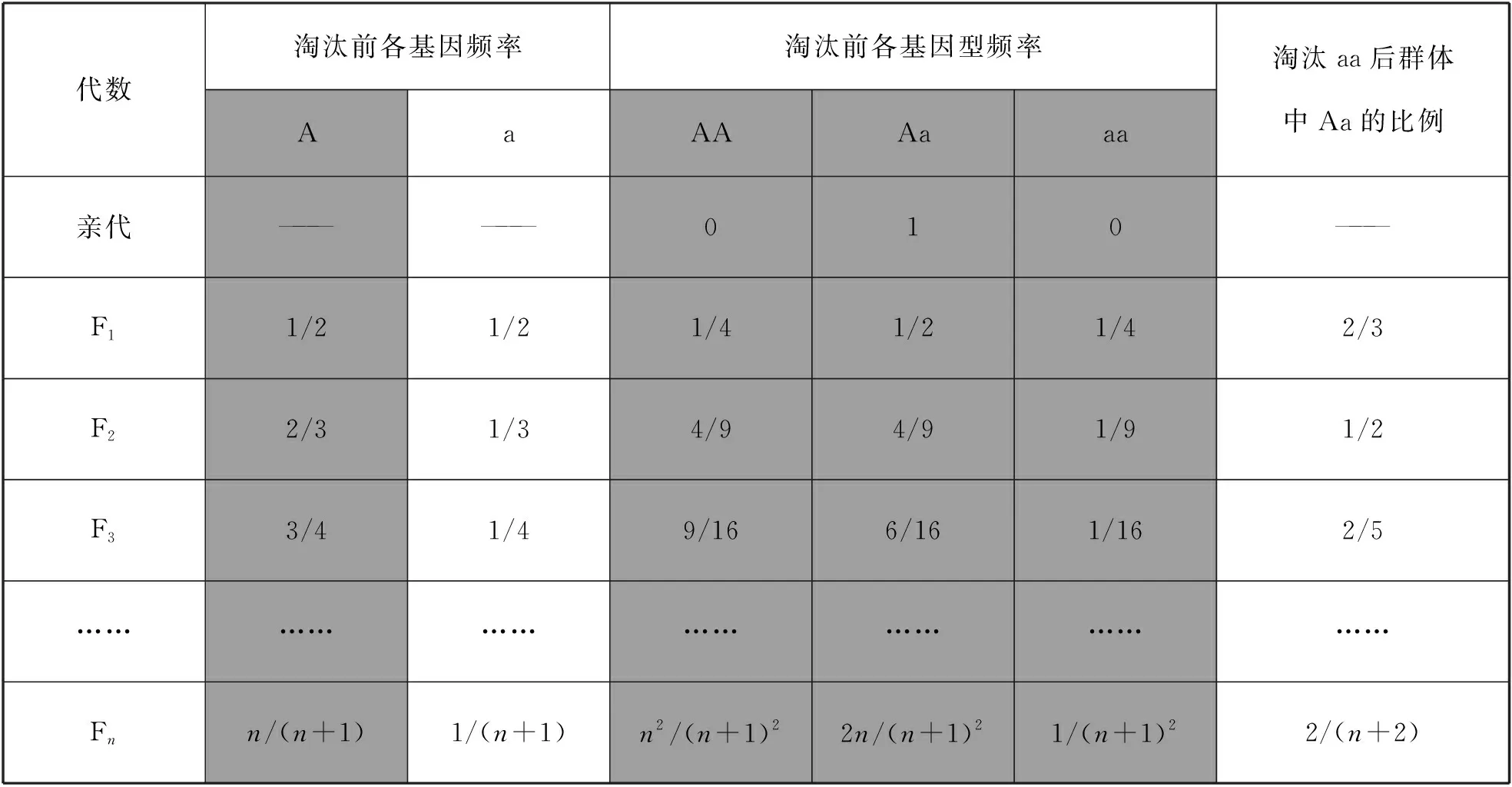
表1 例1的常规解法求解过程

观察表1规律,归纳出答案2/(n+2),并用数学归纳法加以证明。

简便公式法简便公式适用于遗传平衡群体,而本题中存在定向选择(淘汰aa),是否仍能使用呢?从图1乙可知,简便公式求解的是A_中Aa的比例,是否真实淘汰aa并不影响Aa在A_中的占比。不同的是,当aa真正被淘汰后,m、n的值会发生改变,而群体将通过随机交配达到新的平衡。因此,求解本题时,需对每一代使用一次简便公式。但较之常规解法,它省去了表1中灰色底纹的所有计算步骤,因而更为便捷。

4.1.2淘汰AA

例2.Aa连续随机交配,且AA完全致死,求n代后群体中Aa的比例。

从表面看,本题要求的是Aa在_a(Aa+aa)中的比例,而非在A_(AA+Aa)中的比例,似乎无法使用简便公式。但若将A与a对调,便会发现例2与例1完全一致,也适用简便公式,只不过例2所用的m/n指的是A基因频率。

对比例1、例2可知,特定群体中杂合子(Aa)的比例与A、a的显隐性无关。简便公式不仅适用于以a基因频率计算Aa在A_(去除aa的群体)中的比例,也适用于以A基因频率计算Aa在_a(去除AA的群体)中的比例。

4.2基因位于性染色体上

当基因位于X染色体上时,遗传平衡群体的矩形面积图如图2所示,灰色表示雌性,白色表示雄性,两者的面积相等。Xa基因频率在雌雄群体中无差异,均为m/n,XA亦然,均为(n-m)/n。由图2不难看出,雌性群体的矩形面积图(灰色)符合矩形拼接条件,故而适用简便公式;雄性群体的矩形面积图不符合拼接条件,不适用简便公式。雄性群体中由于不存在杂合子Aa,也无需考虑Aa占比问题。

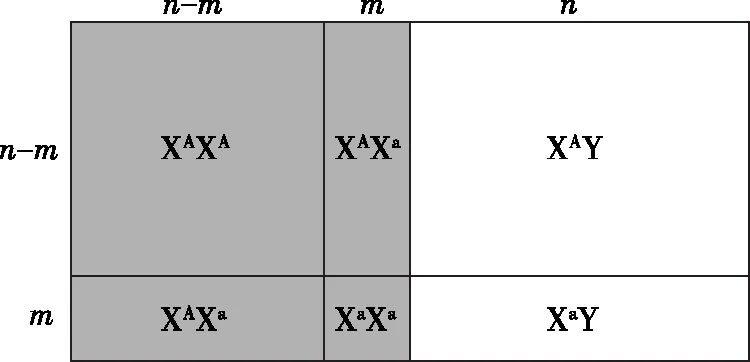
图2 X染色体上基因的矩形面积图

例3.在中国,男性群体中红绿色盲率为7%。求一对表型正常的夫妇,生出红绿色盲孩子的概率是多少?

解析:男性群体中红绿色盲率为7%,说明色盲基因Xa在男性中的基因频率=7/100。由于遗传平衡群体中基因频率不存在雌雄差异,故女性群体中Xa的基因频率也是7/100。根据简便公式,表型正常的女性人群(XAX-)中XAXa占14/107。一对表型正常的夫妇生出红绿色盲孩子的概率=14/107×1/4=7/214。

通过上述分析可知,对于XY型性别决定的生物,简便公式适用于雌性(XX)。同理,对于ZW型性别决定的生物,简便公式适用于雄性(ZZ)。也就是说,若基因位于性染色体上,则简便公式适用于拥有同型性染色体的性别群体。

4.3复等位基因

复等位基因(如决定ABO血型的IA、IB、i基因)的矩形面积图如图3甲所示。

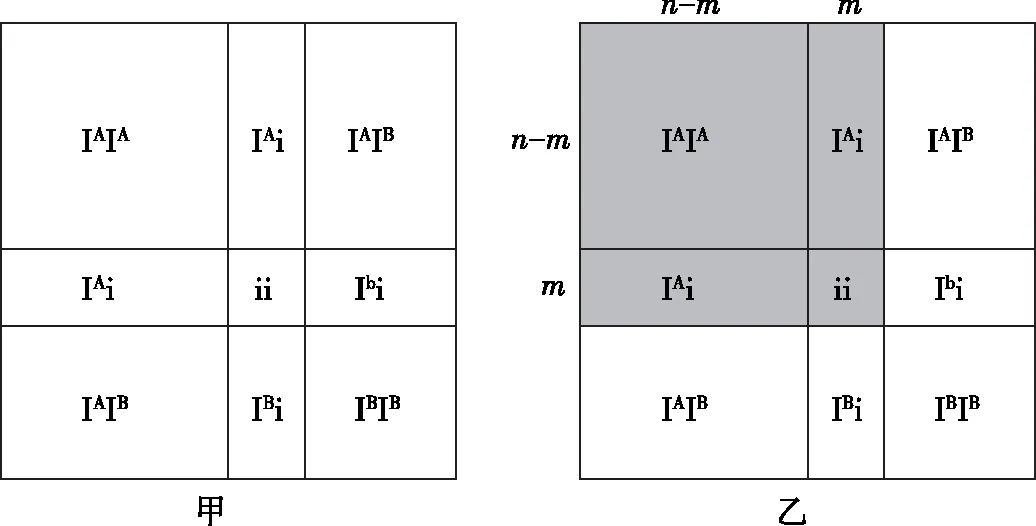
图3 复等位基因的矩形面积图

在图3甲的九个小矩形中,由IAIA、IAi、IAi、ii组成的图形符合矩形拼接条件,适用简便公式;由IBIB、IBi、IBi、ii组成的图形同理。调换某些小矩形的位置后,还会发现由IAIA、IAIB、IAIB、IBIB组成的图形亦然。这说明,当所研究的群体只由复等位基因中的两种组成时,简便公式可用。需要说明的是,此时的m/n不是该基因在所有等位基因中的比例,而是在所涉及的两种等位基因中的比例(图3乙,以IAIA、IAi、IAi、ii为例)。

例4.某遗传平衡的人群中,O型血占36%,AB型血占6%。求A型血人群中杂合子的比例?

解析:遗传平衡人群中,O型血占36%,说明i的基因频率r=3/5,IA、IB的基因频率之和p+q=2/5。又因为AB型血占6%,即2pq=3/50,可求出IA的基因频率p=1/10或3/10。当p=1/10时,i占(IA+i)的6/7,根据简便公式,A型血人群(IAIA+IAi)中杂合子IAi占(6+6)/(7+6)=12/13。当p=3/10时,i占(IA+i)的2/3(6/9),根据简便公式,A型血人群中杂合子占4/5。

5.小结

借助矩形拼接法,可归纳出简便公式的适用条件:①大正方形的每条边都被分割成特定比例的两份,说明所研究的群体(可以是总群体的一部分,如图2、图3)在该基因座位上只含有两种等位基因,且基因频率在雌雄群体中无差异。②大正方形被分成四个小矩形,说明雌雄个体间随机交配。③在不考虑p=q的情况下,四个小矩形中的两个是大小不等的正方形,另两个是形状大小完全一致的长方形,说明群体中存在三种基因型,分别是两种纯合子和一种杂合子(图1甲、图2灰色部分、图3乙灰色部分)。④所求群体由杂合子和一种纯合子组成(图1乙、丙),而作为已知条件的m/n是另一种纯合子所含基因的频率。⑤简便公式还可用于求解④群体中纯合子的比例,方法是先用公式求出杂合子比例,再用1减之,无需记忆其他公式。