金融市场典型事实下的金融资产回报实证研究

郑紫璇

摘要：随着世界贸易一体化进程加快和经济全球化发展深化，国内外啤酒业的投资与建设不断加速。后疫情时代的企业必须坚持风险管理原则辅以基本的定量研究方法以维持公司业绩和企业竞争力。文章选取世界最大的跨国酿酒公司之一A公司进行定量分析，将金融资产回报相关的典型事实纳入考察，其中大部分内容将旨在调查被定义为基于经验发现以简化演示的典型事实。文章实证归纳出包括自相关缺乏（Absence in Autocorrelation）、尖峰胖尾（Leptokurtosis and Fat-tailed）、绝对回报中自相关的缓慢衰减（Slow decay of autocorrelation in absolute returns）、波动聚集性（Volatility Clustering）和聚合高斯性（aggregational gaussianity）的五类金融資产回报相关的典型事实有效，但部分概念在具体细节上缺乏准确性。

关键词：典型事实；时间序列；定量研究；风险管理

一、引言

啤酒生产在大多数国家都很普遍，消费率在很大程度上影响着啤酒生产速度和公司股价，进而为企业风险管理带来机遇与挑战。大多数学者如Schwert， 都对股票收益率和工业生产数据的关系进行了系统研究。Lazarus则从行业层面的角度出发，指出当前行业的金融资产回报与未来工业生产增长率间存在密切关系。现有研究从多方面实证啤酒的消费生产速率波动会引发包括股价变动在内的各种风险进而影响企业价值，但较少有基于金融资产回报典型事实视角的企业风险管理研究。典型事实作为能够真实反映经济运行的基本特征且具有代表性的关键性事实，标志着新时代经济理论发展的新方向，对于数字经济时代的企业风险管理至关重要。而基于金融时序的典型事实涉及使用过去的数据以预测未来，此中提及的“预测”与企业风险管理流程是密切相关的，而基于金融时序的分析可以高度涵盖和确定未来生成的实际利润和相关风险。因此，验证和筛选出能够为风险管理提供有效信息的金融资产回报相关典型事实，成为问题的关键。本研究将上列各项问题再次纳入，尝试运用定量分析方法，揭示有关金融资产回报的五个典型化事实并核实以确定可能不准确的细节，具体包括自相关缺乏（Absence in Autocorrelation）、尖峰胖尾（Leptokurtosis and Fat-tailed）、绝对回报中自相关的缓慢衰减（Slow decay of autocorrelation in absolute returns）、波动聚集性（Volatility Clustering）和聚合高斯性（aggregational gaussianity），以期为未来的理论研究与风险管理策略制定提供一些有益的借鉴和具有可操作性的实证方法。

二、数据选取与处理

（一）数据选取

在大多数情况下，合适的时间截取能够呈现最优的数据结果，因此变量的选取需充足周全，受疫情影响，对酿酒业，特别是以A公司为首的大型跨国啤酒供应商冲击巨大，样本数据来源于雅虎财经数据库，截取自2013～2020年的A公司股票价格日报，其中没有缺少的日期，并将时间设定为独立变量。

（二）数据处理

因金融资产回报中的波动率指标无法直接被观察，为便于后续分析其收益状况，并保证研究的样本序列的平稳性，本文将A公司股票价格样本序列做对数差分变换，从而得出此金融资产回报的收益率序列，即：

rt＝logpt-logpt-1 （1）

其中，rt表示时间t时刻的收益率，pt表示时间t时刻的A公司股价，pt-1表示时间t-1时刻的A公司股价。

此外，本研究还做如下两点处理：

1. 自相关和自协方差

时间序列Xt的自协方差定义为 r（k）=Cov（Xt，Xt-k），其协方差定义为Cov（Xt，Xt-k）=E（Xt-E（Xt））（Xt-k-E（Xt-k）。因本文专门研究的是剔除E（Xt）=0条件下的典型事实，所以在所有模型中，可认为r（k）=E（Xt-Xt-k）。另外，r（o）=var（Xt）。综上，自相关函数作为表达Xt和Xt-k相关性的一个相对统计量，具体公式如下：

p（k）=Cov（Xt，Xt-k）/sqrt of Var（Xt）Var（Xt-k）

=E（Xt，Xt-k）/Var（Xt）

=r（k）/r（o）

这些符号假设Cov（Xt）和Xt-k与Xt-1和Xt-k-1是相同的，即结果只依赖于两个Xs和k之间的离散程度，而非绝对日期。基于此，验证了可逆ARMA模型的属性。

2. 稳定性

最基本的稳定性检验方法依赖于绘制数据或其函数，并从视觉上确定它们是否呈现了平稳数据的某些已知属性。序列可被分为强平稳性和弱平稳性两种形式。严格来说，当{Xt}的联合概率不受时间基准变化的影响，即它是与时间相关的（time-invariant）或不因时间基点（time joint）变动时，此时间序列被认为有强平稳性。

具体而言，时间序列中的任何一组时间t1，t2，t3，t4…tm的联合概率分布必须与时刻 t1+k，t2+k，t3+k，tm+k的联合概率分布相同，其中k表示循着时间轴的任意移位。此外，m=1表示边际概率分布不依赖于时间t；m=2表示所有单变量分布都不依赖于时间t，此时

COV（x1，x1+k）= cov（x1，x2+k）=…=cov（xm，xm+k）

其中，自协方差和自相关取决于时间差k，即

r（k）=cov（xt-k，xt）=e（xt-k-u）（xt-u）=p（k）

p（k）=cov（xt-k，xt）/sqrt of var（xt-k）var（xt）

=r（k）/r（o）

*公式p（k）=r（k）/r（o）中，r为γ（gamma），p是rho。

三、金融资产回报特征分析

（一）收益率曲线与收益率特征分析

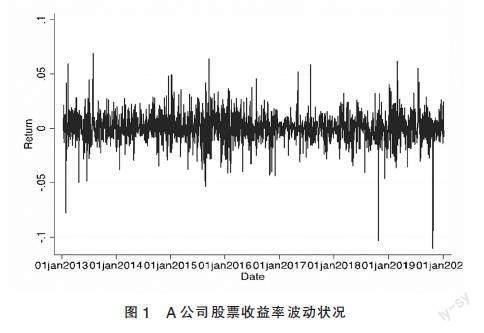
根据公式 （1） 对A公司日度历史股价进行对数差分处理后，股票收益率的描述性统计与收益率波动状况的时间序列图，具体如表1与图1所示。

综上得出，一是收益率曲线围绕着0上下波动的形态，并随着时间的变化而产生不同程度的变化，呈现出显著的时变性、波动聚集性及非线性的特征。二是A公司股票收益率均值较小，均值与标准差相差较小，该股票交易价格稳定性尚可，但价格呈下降趋势。三是观察偏度值，说明收益率为左偏分布。四是研究样本收益率的峰度远大于三，呈现“高峰肥尾”特征，市场风险相对较大。

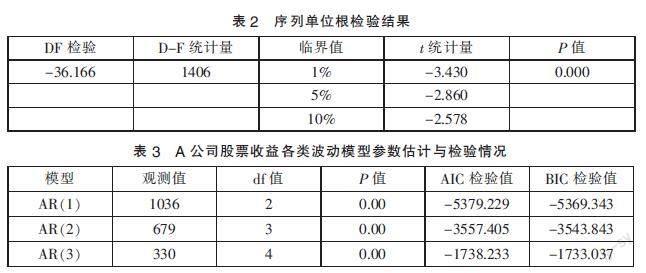
从图1的直观表象及表1的描述性统计特征值，不能识别明显的季节性，数据初步印象无法作为检测平稳性的可靠的方法，本文选择富勒检验模型进一步验证，测试目标序列自回归模型中的单位根目录，原假设H0为：存在单位根（非平稳）。表2显示Z test值都小于各置信度检验的临界值，且p-value为0.0000显著低于5％，应拒绝原假设H（0），样本平稳性得以证明。

（二）估计方法及检验结果

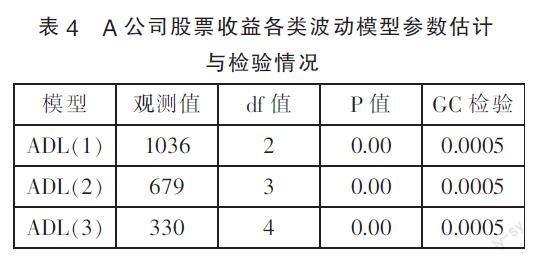
首先，风险经理可使用自回归模型对金融资产进行预测，假设该股票的买卖双方将受到最近市场交易的影响，以确定证券的接受价格。本文利用Akaike的赤池信息准则（AIC）和贝叶斯信息准则（BIC）来确定最佳的AR模型。AIC和BIC模型都建立在Claude Shannon的信息论基础上，却又有所差异，AIC准则建立在熵的概念基础上，以期从预测角度选择更优模型，而BIC准则从拟合角度，选择对现有数据拟合最好的模型。AIC与BIC的值越小，即丢失的信息越少，呈现出来的价值就越低。由表3可知AIC和BIC检验下的AR模型（1）的值最低，可被确定为最佳的自回归预测模型。

由于样本序列经检验是平稳的，因而可以用格兰杰因果检验进行“自下而上”的估计，假定任何时序中的数据生成过程都为一个自变量以探究关联性。格兰杰因果检验结果见表4，结果显示，P值都为0.0005，绝对小于5%的显著值，证明收益率对交易量有显著影响。格兰杰因果关系检验在实操中易于实现，并具有良好的统计基础，但此检验的局限性在于无法给出确切的预测结果。

由于格兰杰因果检验并没有得出一致性的结论，因而决定用包含解释变量当期值的 ADL模型再次进行检验，自回归分布滞后模型（ADL）通过绘制每个时期的资本流动总额，以揭示交易量与实际价格之间的差异，从而确认此金融资产回报的当前的主要趋势或预期的未来逆转。作为动态单方程回归的主要工具，ADL被定义为一个基于成交量的指标，其本质是为了衡量潜在的供求关系。通过合并分析三种ADL模型，结果如表4显示，变量d-滞后L1，L2，L3的p值均为0.000，均显著小于5%，证明不能使用这些变量作为参数。究其缘由可能是由于样本截取的7年间日股票价格数量过大，由此致使滞后数量巨大而导致的误差连续不相关。

（三）典型事实的有效性检验

本研究使用日度股票历史价格作金融时序分析，因此适用于的主张，以下重点检验分析五个典型事实的有效性，依次为：自相关性缺乏、在绝对回报中自相关的缓慢衰减、尖峰胖尾、波动聚集性和聚合高斯性。

1. 自相关缺乏（Absence in Autocorrelation）。“自相关性缺乏”指资产的线性或自相关回报通常是无关的，除非变量受到微观结构的影响，例如，现实情况中股票的盘中时间可以扩展到20分钟。Rois等人的研究指出只有Breusch-Godfrey（BG）检验才能检验随机回归变量的存在性。原假设H（0）为：无自相关，BG检验结果P值为0.1690，在5%水平上拒绝“无自相关”原假设，即存在一阶自相关，典型事实有效。

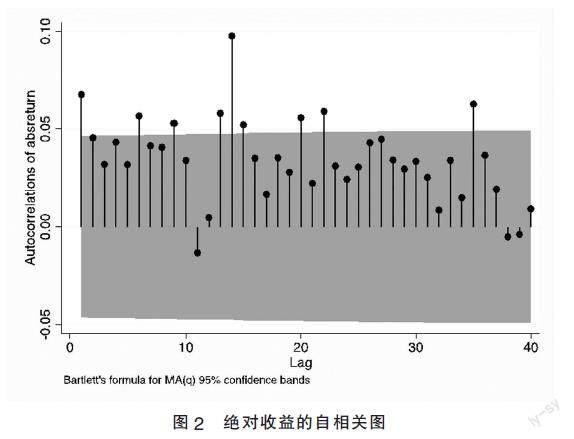
2. “绝对回报中，自相关性的缓慢衰减”指金融资产回报收益随自相关函数的缓慢衰减将被用作近似于幂律指数β∈[0.2，0.4]的时间函数，这有时被解释为长期依赖的迹象。图2中最直观的发现为线的集中分组，表明了绝对收益与自相关函数的近似相似，这与Cont的观点一致。Thompson在进一步的研究中指出，绝对收益率自相关的缓慢衰减可能与一个经历时段较长的平稳过程后的股票收益率相一致。举例而言，许多发生在观测时间之前的事件实际上与当前金融资产相关的收益率动态相关。此外，商业环境中的从众心理也可能是影响因素之一。

3. “尖峰胖尾”指在大多数研究数据集中金融资产相关回报的（无条件情况下）分布似乎显示了一个幂律或类似帕累托（Pareto） 的尾巴，尾部指数被限制在2～5的范围内。在回报的分布检验结果中应显示不存在具有无限方差和正态分布的稳定性定律。研究并确定尾巴的确切形式是异常困难的，因此本文选用峰度检验调查此典型事实的有效性。表1显示的样本峰度系数为8.99236远大于3，说明了样本数据为重尾分布。此外，利用偏态和峰度检验对样本的正态性进行辩证的证明，结果显示偏度和峰度P值均为0，小于5%的显著值，应拒绝关于正态分布的H（0）。基于此被充分记录的样本数据，重尾事实的有效性得以证明。

4. “波动聚集性”意味着不同的波动性度量在特定的时间尺度上呈正自相关，量化的事实将证明高波动性事件倾向于呈现在时间上的聚类。由图3可得，高回报自相关指数与低回报自相关指数之间的部分差值较大，结果显示，与波动性聚类典型事实相一致。可以推断，当金融资产回报相關的时间序列发生大事件时，其自相关也会相应发生变化。

5. “聚合高斯性”意味着当增大计算金融资产收益的时间间隔时，其分布形态会趋于正态分布。金融资产回报在不同的时间尺度基准下反映的分布形状是不同的，因此本文使用基于相同时间范围的不同时间轴基准进行测试（2013～2020年）。其中，另外两个时序数据以每周和每月划分，并分别对三类时间序列进行峰度检验。由于前文已证明了该金融时序的“胖尾尖峰”典型事实，因此本节仅使用峰度检验调查周度和月度序列的峰度。通过比较三类不同时间轴基准的时序峰度，对金融资产回报的聚合高斯分布这一典型事实进行验证。结果显示，周度时间序列的峰度检验结果为4.125942，属于重尾分布，在偏态和峰度检验正态分布的辩证检验中峰度P值为0.0014，低于5%，再次证明其不处于正态分布；月度时间序列的峰度检验结果为3.321294，峰度检验的P值为0.3549，低于5%，样本不属于正态分布。总结发现得出，无论是日、周还是月度时序，结果都与正态分布不一致；月度、周度到日度的金融时序峰度与3的偏差逐渐减少。上述实证结果与聚合高斯性一致，典型事实成立。

四、结语

综上所述，本研究实证证明金融资产回报相关的时间序列与五个典型事实相一致。但在实际应用中，金融时序的分析也有局限性，例如，当外部因素有限时不能被使用。对于企业风险管理者而言，应重点关注在极端风险测度中具有很高应用价值的收益率自相关性、胖尾分布和有偏分布等典型事实，时刻警惕极端风险的爆发并及时预防和化解极端风险，监测它们的特征及变化情况。对于监管部门而言，可根据这些典型事实的特征与变化，选择适当的模型以预测和分析，以期准确测度市场风险，并制定相应的管理措施。此外，投资者可根据这些典型事实的特征及变化，鉴于自身风险承受能力和风险容忍度确定覆盖率水平以选择合适的模型测度和预测风险，制定或调整合适的投资策略，提升风险管控能力。

参考文献：

[1]Schwert G W，Seguin P J.Heteros-kedasticity in stock returns[J].the Journal of Finance，1990，45（04）：1129-1155.

[2]French J.The time traveller’s CAPM[J].Investment Analysts Journal，2017，46（02）：81-96.

[3]Box G E P，Jenkins G M，Reinsel G C，et al.Time series analysis：forecasting and control[M].John Wiley & Sons，2015.

[4]Chatfield C.The Analysis of Time Series：An Introduction[J].CRC Press，2004.

[5]Shannon C E.A mathematical theory of communication[J].Bell Systems Technol，1948，27（03）：379-423.

[6]Hassler U，Wolters J.Autoregressive distributed lag models and cointegration[J].Modern econometric analysis.Springer，Berlin，Heidelberg，2006：57-72.

[7]Cont R.Empirical properties of asset returns：stylized facts and statistical issues[J].Quantitative finance，2001，1（02）：223.

[8]Rois R，Basak T，Rahman M M， et al.Modified Breusch-Godfrey Test for Restricted Higher Order Autocorrelation in Dynamic Linear Model-A Distance Based Approach[J].International Journal of Business and Management，2012，7（17）：88.

[9]Thompson S.The stylised facts of stock price movements[J].The New Zealand Review of Economics and Finance，2011，1.

＊本文系衢州职业技术学院校级重点科研项目“基于ERM-COSO模型的两山银行风险管理研究”（项目编号：QZYZ2109）阶段性研究成果。

（作者單位：衢州职业技术学院）