跨期决策中的维度差异偏好:眼动证据*
刘洪志 杨钘兰 李秋月 魏子晗
跨期决策中的维度差异偏好:眼动证据*
刘洪志4,5杨钘兰4李秋月4魏子晗1,2,3
(1天津师范大学心理学部;2教育部人文社会科学重点研究基地天津师范大学心理与行为研究院;3学生心理发展与学习天津市高校社会科学实验室, 天津 300387) (4南开大学周恩来政府管理学院社会心理学系, 天津 300350) (5南开大学经济行为与政策模拟实验室, 天津 300071)
在跨期决策研究领域, 虽然基于维度的跨期模型得到了一些源自结果检验和过程检验的证据支持, 但此类模型所假设的维度间差异比较的心理过程尚缺乏直接的过程证据。本研究通过两个眼动实验, 系统考察了相关眼动指标对维度差异偏好的预测效应。结果发现, 根据基于维度的权衡模型可有效拟合出个体在跨期决策中的维度差异偏好, 并且反应时、眼跳注视熵和静态注视熵等指标均与维度差异偏好负相关, 而基于维度的注意分配与维度差异判断正相关。这些研究发现支持了本研究所提出的跨期眼动模型的相关假设, 证实了维度差异偏好与跨期决策的认知加工过程之间的联系, 为基于维度的跨期模型提供了更直接的过程证据, 并为今后跨期决策的眼动模型发展指明了新方向。
跨期决策, 基于维度的跨期模型, 维度差异偏好, 眼动追踪技术
1 引言
人们往往会面临近期收益与远期收益之间的权衡与取舍, 这种对发生在不同时间点(尤其是现在与未来之间)的结果进行权衡, 从而做出判断和选择的决策过程称为跨期决策(intertemporal choice) (Frederick et al., 2002; 何贵兵等, 2009; 梁竹苑, 刘欢, 2011)。例如, 是选择当下消费以满足即刻需要还是选择储蓄以获取未来更大收益(Dai & Busemeyer, 2014; Zhou et al., 2021)。在跨期决策的研究中, 研究者通常要求个体在一个小而近(smaller- sooner, SS)和一个大而迟(larger-later, LL)的选项间进行抉择, 以考察个体的跨期偏好(Scholten & Read, 2006; Scholten & Read, 2010; 江程铭等, 2016)。例如, 是选择“即刻获得100元” (SS选项)还是选择“1个月后获得150元” (LL选项)。
1.1 基于选项与基于维度的模型
传统的跨期决策理论认为, 在面临跨期决策时, 人们会将未来结果按一定比率折扣到现在, 比较各个选项折现后的价值并做出决策。例如, 经济学家Samuelson (1937)提出的第一个理性跨期模型——折扣效用模型(discounted-utility model)认为, 决策者会按照恒定的比率(即时间折扣率)对未来结果的效用进行折扣(江程铭等, 2016; 梁竹苑, 刘欢, 2011)。随后, 由于诸多违背折扣效用模型的异象(anomalies)的发现, 研究者在折扣效用模型的基础上对折扣函数进行了修正, 发展出了双曲线折扣模型(Ainslie, 1975; Frederick et al., 2002; Loewenstein & Prelec, 1992)、准双曲线折扣模型(Laibson, 1997)等修正模型。虽然这些模型的折扣函数不同, 但它们均假设跨期决策采用基于选项的(alternative- based)加工过程, 即决策者会计算各选项的折扣值并进行比较, 最终选择折后效用值最高的选项。因此, 这类时间折扣模型可统称为基于选项的跨期模型。
也有研究者从决策过程的角度出发, 认为个体的跨期决策并非如时间折扣模型所设想的那样理性, 而是采取一些基于直觉的启发式策略, 并在此基础上提出了一系列模型, 如属性比较模型(attribute-comparison model) (Read, 2001)、相似性模型(similarity model) (Leland, 2002)、权衡模型(tradeoff model) (Read & Scholten, 2012; Scholten & Read, 2010)、齐当别抉择模型(equate-to-differentiate model) (Li, 2004, 2016)等。以权衡模型和齐当别抉择模型为例, 二者均假设个体在跨期决策时会比较结果维度和延迟维度之间的相对差异大小。如果决策者认为结果维度的主观差异较大, 即选择在结果维度上占优的LL选项; 反之, 如果认为延迟维度的主观差异较大, 即选择在延迟维度上占优的SS选项。这些模型均假设跨期决策采用一种基于维度的(dimension-based)加工过程, 即决策者会比较不同维度间的差异, 并在此基础上做出决策。因此, 这类模型可统称为基于维度的跨期模型。
1.2 基于维度的跨期模型缺少足够过程证据
近年来, 研究者一直致力于检验并比较以上两类模型。一方面, 一些行为学证据更支持基于维度的跨期模型。例如, Scholten和Read (2010)发现, 基于维度的权衡模型可以解释时间折扣模型所不能解释的次可加性(subadditivity)和超可加性(superadditivity)现象。一些研究者采用跨期决策的行为结果对不同跨期模型进行数据拟合, 亦发现基于维度的模型比基于选项的模型表现更优, 能更好地拟合人们的跨期决策行为(Cheng & González- Vallejo, 2016; Dai & Busemeyer, 2014; Ericson et al., 2015; Scholten et al., 2014)。另一方面, 由于眼动追踪技术的优越性(魏子晗, 李兴珊, 2015), 一些研究者尝试采用眼动追踪技术为跨期模型的检验提供进一步的过程证据。例如, 有研究发现跨期决策中三分之二的眼跳为基于维度的眼跳(Arieli et al., 2011), 这暗示个体可能分别对结果和延迟维度信息进行了独立加工(Amasino et al., 2019)。也有研究者发现操纵基于维度的眼动注视可影响跨期决策行为, 验证了基于维度的信息加工对跨期决策的因果效应(Fisher, 2021; Liu, Lyu, et al., 2021; Reeck et al., 2017), 这提示基于维度的信息加工在跨期决策中起了重要作用。
虽然基于维度的跨期模型已得到一些来自眼动过程证据的支持, 但仍有两个问题尚待解决。第一, 对于基于维度的模型所假设的维度间差异比较的心理过程, 尚缺乏更直接的过程证据。以往的眼动研究多关注于基于维度的注视或眼跳与跨期决策行为之间的关系(如Fisher, 2021; Reeck et al., 2017), 而少有研究关注维度差异比较这一心理过程。尽管多数研究者认同跨期决策中存在维度间差异比较的心理过程(Arieli et al., 2011), 但这一心理过程能否反映于眼动注视尚未明确。若能捕获维度间差异比较与眼动注视之间的关系, 则可为基于维度的跨期模型提供进一步的过程证据支持。第二, 基于维度的注视与跨期决策的关系尚待进一步检验。尽管很多眼动证据支持基于维度的跨期模型, 但也有研究发现, 基于维度的注视时间优势并不能显著预测随后的跨期决策行为(Liu, Lyu, et al., 2021)。这可能是由于基于维度的注视与维度间差异比较的关系尚不明确所致, 若能厘清二者关系, 或可帮助理解跨期决策的信息加工过程, 为跨期模型的进一步发展提供证据参考。
1.3 维度差异偏好与眼动模型
针对以上问题, 本研究采用眼动追踪技术, 考察了跨期决策中的维度间差异比较与信息加工过程的关系, 以期为基于维度的跨期模型提供进一步证据。根据基于维度的跨期模型, 个体的跨期决策行为取决于其维度差异判断的程度, 即“两个维度的差异究竟有多大”。据此, 本研究提出维度差异偏好(preference of dimension-based difference, PDD)的概念, 用于表示个体在二择一跨期决策中对结果与延迟维度的主观差异相对大小的判断。本研究关注维度差异偏好是否可反映于与信息加工过程相关的眼动指标上。
近年来, 一些学者提出了结合眼动注视的注意漂移扩散模型(attentional drift-diffusion model, aDDM), 并验证了该模型在单维决策中的良好解释力(Krajbich et al., 2010; Krajbich et al., 2012; Krajbich & Rangel, 2011)。该模型假设, 决策者通过随机的眼动注视对选项信息进行抽样(sampling), 并累积选项的证据, 当某一选项累积的证据达到阈限时即做出决策, 选择累积证据较大的选项(Krajbich et al., 2010)。有研究者基于这一理论视角, 发展出了基于维度的跨期漂移扩散模型, 并用反应时数据进行拟合(Amasino et al., 2019), 这表明基于顺序抽样模型的思路去解释跨期决策的信息加工过程是可行的。结合基于维度的跨期模型以及aDDM的研究视角, 本研究提出, 跨期决策或可假设为基于眼动注视对维度差异信息进行抽样并累积证据的过程。当某一维度(结果或延迟维度)所累积的证据达到阈限, 即根据该维度进行决策。根据这一跨期版aDDM (intertemporal aDDM, iaDDM)模型, 维度差异偏好也可反映于信息加工过程中。de Martino等(2013)基于漂移扩散模型的拟合数据, 发现个体达到决策阈限时在两选项上累积证据的差异可定量反映其决策信心程度。鉴于决策信心与维度差异偏好在理论上的相关性, 本研究提出, 维度差异偏好可反映于决策者在达到决策阈限时对两维度累积证据的差值上。
1.4 研究假设
根据iaDDM模型, 本研究从以下4方面提出研究假设。
首先, 本研究根据基于维度的跨期模型, 对维度差异偏好进行定量估计。本研究选取基于维度的模型中表现优异的权衡模型作为拟合模型(Read & Scholten, 2012; Scholten & Read, 2010)。前人多采用“模拟天平”范式测量跨期决策中的维度差异偏好。该范式借助比喻形象地表征跨期决策中两维度的相对差异大小, 要求被试用7点量表来选择不同倾斜程度的天平, 以表征其主观维度差异判断(江程铭等, 2016)。为验证本研究所采用的维度差异偏好的估计方法的有效性, 本研究将模拟天平范式所测得的主观维度差异判断作为校标。据此, 本研究假设: 基于权衡模型所估计的维度差异偏好与天平判断相关(H1)。
其次, 本研究认为, 反应时可反映跨期决策的维度差异偏好。反应时作为行为学实验中最常用的指标之一, 可反映决策的认知加工过程。有研究者将反应时作为反映偏好强度的指标, 发现反应时与偏好强度负相关(Diederich, 2003; Konovalov & Krajbich, 2019; Tversky & Shafir, 1992), 即个体对某选项的偏好强度越大, 反应时越短。其理论逻辑是, 个体对某选项的偏好强度越大, 往往意味着两选项的价值差异越大, 因此在顺序抽样过程中需较短时间即可达到决策阈限, 进而做出选择。类似地, 本研究认为, 根据iaDDM模型, 当个体认为某一维度的相对差异越大, 即维度差异偏好越大时, 累积证据达到阈限所需的时间越短, 即反应时越短。据此, 本研究假设: 反应时与维度差异偏好负相关(H2)。
第三, 本研究认为注视熵可反映跨期决策的维度差异偏好。注视熵(gaze entropy)是基于信息理论(Shannon, 1948)对个体在任务中的信息搜索模式进行定量估计的眼动指标(Shiferaw et al., 2019)。相比于注视次数、平均注视时长等传统眼动指标, 注视熵作为整合性指标, 可对任务中的信息搜索模式进行整体性估计, 从而降低研究结论的情境依赖性, 并减小数据噪声(Shiferaw et al., 2019)。因此, 本研究尝试考察注视熵对维度差异偏好的敏感性。常用的注视熵指标有两个(Cuve et al., 2021; Shiferaw et al., 2018), 一是眼跳注视熵(gaze transition entropy), 它衡量的是兴趣区之间随机眼跳的频繁程度(Krejtz et al., 2014; Shiferaw et al., 2019), 反映了信息搜索的效率(Shiferaw et al., 2019), 其值越大, 个体的信息搜索效率越低; 二是静态注视熵(stationary gaze entropy), 它衡量的是不同兴趣区之间注视分布的均匀程度(Krejtz et al., 2014), 其值越大, 注视分布越均匀。根据iaDDM模型, 当两维度的累积证据相差较小时, 往往需要更多注视去累积证据以达到阈限, 从而导致更长的搜索时间和更频繁的眼跳。与之相反, 当两维度证据相差较大时, 决策者在有限的注视时间内即可达到决策阈限, 其注视分布相对更不均匀。因此, 维度差异偏好越大, 意味着个体在不同维度间的信息搜索越少, 即眼跳注视熵越低, 亦意味着维度间的注视越不均匀, 即静态注视熵越低。据此, 本研究假设: 眼跳注视熵和静态注视熵均与维度差异偏好负相关(H3)。
最后, 本研究认为基于维度的注意分配可反映维度差异判断。对不同决策维度的注意分配可反映于不同维度的注视时间差异上(Amasino et al., 2019; Zhou et al., 2021)。根据iaDDM模型, 个体注视某一维度时间越长, 对这一维度所累积证据越多, 从而将该维度的相对差异判断得越大。因此, 本研究假设: 基于维度的注意分配与维度差异判断相关(H4)。
1.5 研究概览
综上所述, 本研究通过2个实验, 采用眼动追踪技术系统考察了跨期决策中维度差异偏好与信息加工的关系, 以期为基于维度的跨期模型提供进一步的过程证据。一方面, 本研究基于权衡模型, 根据个体在二择一跨期决策中的选择结果拟合个体的维度差异偏好, 并通过模拟天平任务测量(实验1)和选择一致性(实验2)等效标验证所估计的维度差异偏好的有效性。另一方面, 本研究基于个体在决策过程中的反应时和眼动数据检验维度差异偏好与信息加工过程的关系。
2 实验1:维度差异偏好的过程证据
实验1旨在考察个体在二择一跨期选择中维度差异偏好与信息加工过程的关系。为验证所拟合出的维度差异偏好的有效性, 本研究选取了“模拟天平”范式作为效标, 该范式已被众多研究验证为从基于维度的跨期模型视角检验主观维度差异的有效指标(江程铭等, 2016; 蒋元萍等, 2022; 刘洪志等, 2015)。
2.1 方法
2.1.1 被试
基于Brysbaert和Stevens (2018)的建议, 对于涉及反应时等指标的多试次认知实验, 每种实验条件应不少于1600试次。本实验中, 每名被试在每种条件下完成36试次, 因此最小样本量为= 45。为提高研究效力, 对所需样本量进行1.5倍校正, 计算所需样本量为= 68。实验招募75名大学生参与实验(平均年龄20.9 ± 2.4岁, 女性61人)。所有被试视力或矫正视力正常, 且实验前签署了知情同意书。实验结束后被试获得15元人民币的基本报酬以及与实验表现相关的额外报酬(1~10元)。研究得到所在单位伦理委员会批准。
2.1.2 实验仪器
实验采用EyeLink 1000 plus眼动仪记录被试的眼动信息, 采样率为1000 Hz。被试用双眼观看实验刺激, 但仅记录一只眼睛(左眼)的眼动信息。实验刺激呈现于分辨率为1024 × 768的17寸液晶显示器上(刷新率为60 Hz)。实验中用腮托固定被试的头部, 以减少头动对眼动的影响。被试的眼睛与屏幕间的距离为58 cm, 其双眼与屏幕边缘的水平视角为36°, 垂直视角为29°。
2.1.3 实验材料
实验刺激为二择一的跨期选择题目。跨期选项的金钱设置为4种固定金额: 1元, 2元, 5元和10元; 时间设置为4种固定延迟: 立即, 5天后, 10天后和20天后。将金钱与时间组合成36对无强占优的选项, 例如“选项A: 立即获得5元; 选项B: 5天后获得10元”。实验刺激见补充材料(网址: https://osf.io/xtbjk/)表S1。
2.1.4 实验任务与流程
实验包含2个任务: 跨期选择任务和模拟天平任务。
首先要求被试完成跨期选择任务, 并记录其眼动信息。在跨期选择任务中, 要求被试选择自己偏爱的选项。为了激励被试认真选择, 告知被试在实验结束后会随机选取其一次选择, 在相应时间给予其额外奖励。在实验开始前先校准眼动仪(采用5点校准和验证, 最大验证误差为0.5°视角), 然后进行2个练习试次, 以帮助被试熟悉实验任务, 随后开始正式实验。每一试次开始时, 屏幕中央会呈现一个圆形注视点用作漂移校准。被试注视该注视点的同时按空格键可触发呈现刺激。每次屏幕上呈现2个跨期选项, 被试观看选项的时间不限, 但要求被试一旦确定选择须尽快按键反应。被试按“F”键选择左侧选项, 按“J”键选择右侧选项。被试按键后, 会呈现选择反馈, 呈现时间1000 ms。实验流程如图1a所示。跨期选择任务包含36个试次, 分为2个组块, 组块间休息2分钟。结果和延迟信息的位置在组块间进行了平衡, 两组块的呈现顺序进行了组间平衡。
被试在完成跨期选择任务后继续完成模拟天平任务。该任务由江程铭等(2016)开发, 可借助天平形象地表征延迟维度与结果维度的相对差异大小。如果被试认为延迟维度的差异大于结果维度的差异, 用向左倾斜的天平来表示; 如果被试认为结果维度的差异大于延迟维度的差异, 用向右倾斜的天平来表示; 如果两者差异相似, 则用水平的天平来表示。该任务要求被试用数字1~7来表示自己的维度间差异判断, 分数越大代表结果维度的差异相对于延迟维度的差异越大。实验题目与跨期选择任务相同。任务开始前有2个练习试次, 以帮助被试熟悉实验任务, 随后进入正式实验。每一试次开始时, 屏幕中央会呈现一个圆形注视点。要求被试注视该注视点并按空格键开始试次。随后在屏幕上方呈现2个跨期选项, 下方呈现模拟天平, 要求被试按键盘上的数字1~7来表示自己的判断。被试按键后, 会呈现反馈界面1000 ms。实验流程如图1b所示。
2.1.5 维度差异偏好的估计
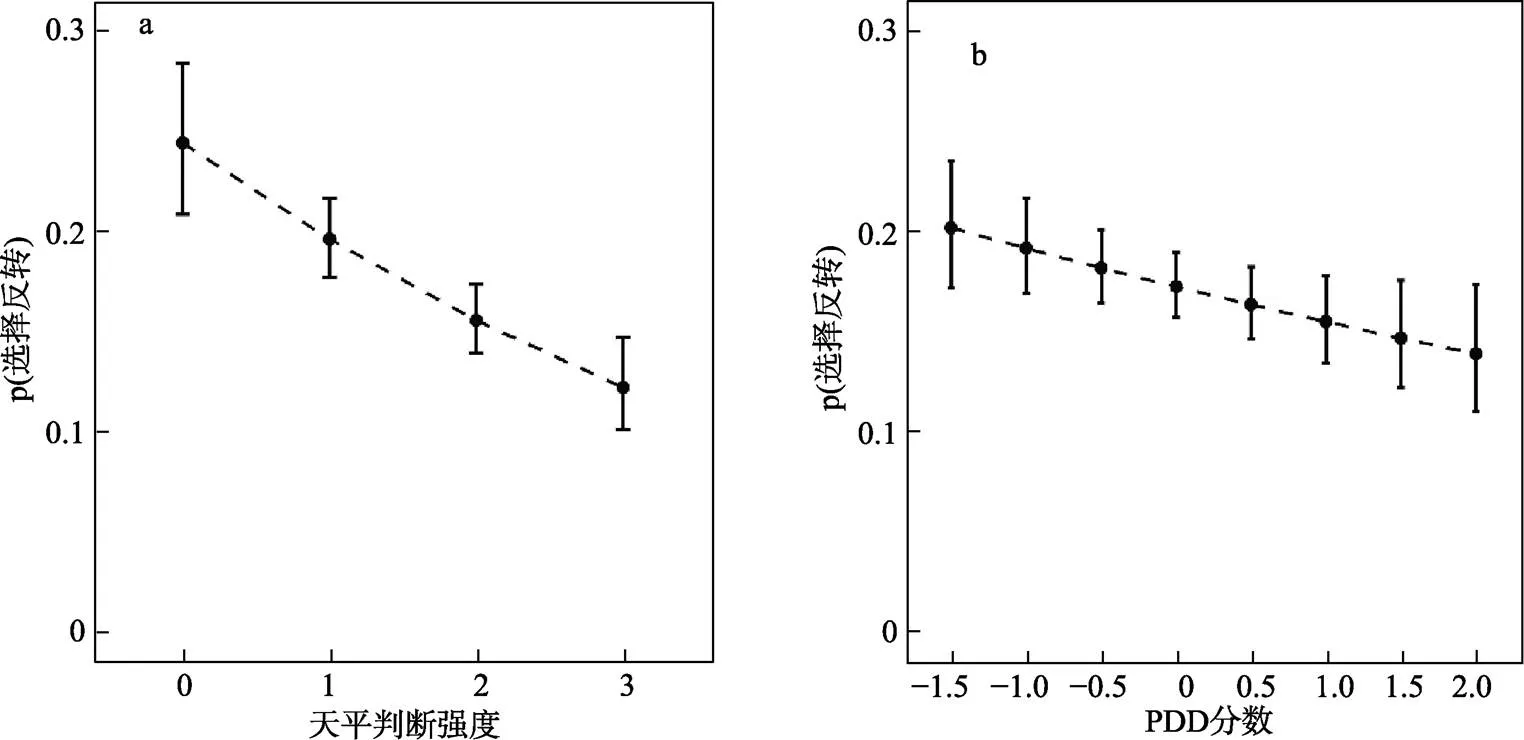
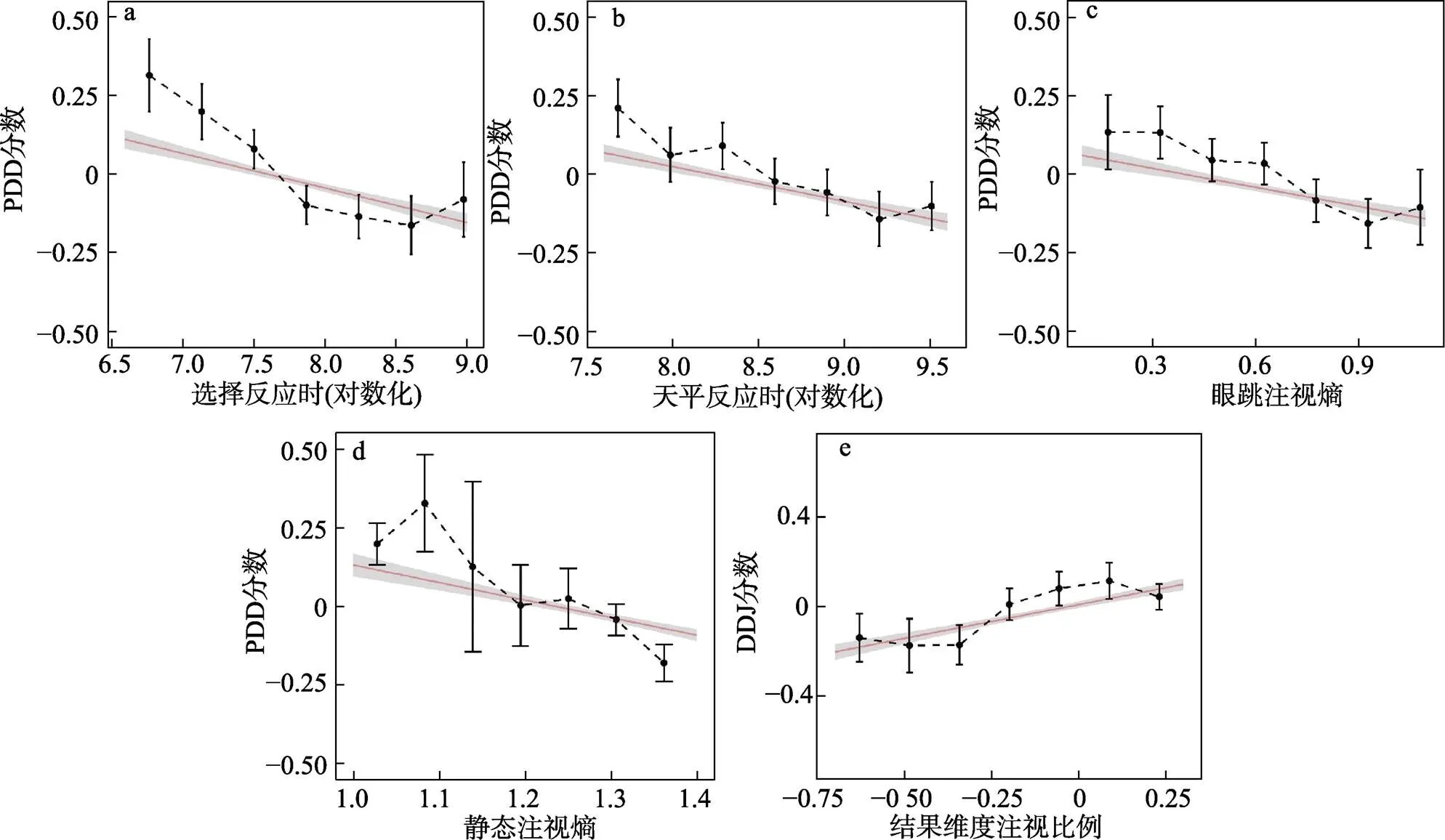
根据被试在跨期选择任务中的选择结果, 基于权衡模型对其在每次选择时的维度差异偏好进行估计。选择权衡模型的原因有二: 第一, 权衡模型能够解释几乎所有跨期异象, 对跨期决策有良好的解释力(Scholten & Read, 2010; Scholten et al., 2014); 第二, 权衡模型所假设的维度差异比较过程与本研究所考察的维度差异偏好的概念相契合。权衡模型认为, 决策者在跨期决策时会权衡结果与延迟维度的相对差异, 并根据差异较大的维度进行决策(Read & Scholten, 2012; Scholten & Read, 2010)。对于二择一的跨期选择: 选项SS为在时间SS后获得SS, 选项LL为在时间LL后获得LL(SS 图1 实验1流程图 其中, 公式左侧为结果维度的主观差异, 右侧为延迟维度的主观差异, 其中κ表示权衡参数, 用于将结果与延迟维度的差异转换为可比较的单位与量级。当结果维度的差异大于延迟维度的差异时, 决策者即选择在结果维度占优的LL选项; 反之, 当延迟维度的差异大于结果维度的差异时, 决策者即选择在延迟维度占优的SS选项。 采用分层贝叶斯方法(hierarchical Bayesian approach)基于个体层面对每个被试的参数进行估计(详见补充材料, 参数估计代码已共享至: https://osf.io/xtbjk/)。随后, 根据所估计的每个被试的参数值, 以及每次选择的选项信息, 计算各被试在每次选择时的两维度差异判断的差值, 即维度差异判断(dimension-based difference judgment, DDJ): 维度差异偏好(preference of dimension-based difference, PDD)即为DDJ的绝对值: DDJ和PDD数值均做标准化处理。 2.1.6 注视熵分析 本研究计算了静态注视熵和眼跳注视熵2个注视熵指标, 详见补充材料(https://osf.io/xtbjk/)。 2.1.7 数据分析 本研究基于R语言环境中的和程序包(Bates et al., 2015; Kuznetsova et al., 2017), 采用混合效应模型(mixed-effect models)对数据进行统计分析。将被试编号和试次顺序作为随机因子, 可增强本研究结果的推广性(Baayen et al., 2008; Judd et al., 2012), 这是以往关于决策的眼动研究中常用的统计方法(Liu, Wei, & Li., 2021; Liu et al., 2020; Sui et al., 2020)。 实验总计2700试次, 其中1试次因眼动追踪失败而在数据分析时被剔除, 共计2699有效试次。 2.2.1 描述性统计结果 被试在跨期选择任务中选择LL选项比例的均值为64.3% (95% CI = [60.2%, 68.5%]), 平均反应时间为4.03 s (95% CI = [3.71, 4.36]); 在模拟天平任务中的判断分数均值为3.67 (95% CI = [3.50, 3.83]), 平均反应时间为7.76 s (95% CI = [7.18, 8.33])。 2.2.2 维度差异偏好与模拟天平分数 为了验证维度差异判断估计的有效性, 将模拟天平任务中的判断分数作为效标, 考察二者的相关性。模拟天平分数可在一定程度上反映个体的维度差异判断, 该分值越大, 表示个体判断结果维度的相对差异越大, 反之, 分值越小, 表示其判断延迟维度的相对差异越大。基于模拟天平分数, 可计算天平判断强度, 即: 天平判断强度 = |模拟天平分数 − 4|, 该分值越大, 表示维度差异偏好越大。 首先, 将被试的跨期选择(选择LL选项记为1, SS选项记为0)作为因变量, 将模拟天平分数作为固定效应, 将被试编号和试次顺序作为随机效应(下同), 做混合模型逻辑回归。结果发现: 模拟天平分数可显著预测跨期选择,= 0.71, 95% CI = [0.64,0.78], OR (Odds Ratio, 似然比) = 2.04,= 20.23,< 0.001, 如图2a所示。这一结果与前人发现一致(江程铭等, 2016), 表明模拟天平任务可有效测量个体的维度差异偏好。 其次, 考察维度差异判断与模拟天平分数的关系。将模拟天平分数作为因变量, 将维度差异判断(DDJ分数)作为固定效应, 做混合模型线性回归。结果发现, DDJ分数的回归系数显著,= 0.80, 95% CI = [0.74, 0.86],= 28.38,< 0.001, 如图2b所示。 最后, 考察维度差异偏好与天平判断强度的关系。将天平判断强度分数作为因变量, 将维度差异偏好(PDD分数)作为固定效应做混合模型线性回归。结果发现, PDD分数的回归系数显著,= 0.23, 95% CI = [0.19, 0.27],= 12.15,< 0.001, 如图2c所示。 以上结果表明, 实验1所拟合的DDJ和PDD分数可有效反映个体的维度差异判断及强度, 支持了H1。 2.2.3 维度差异偏好与反应时 为检验H2, 本研究考察了选择反应时(跨期选择任务中从呈现刺激到被试按键反应的时间)和天平反应时(模拟天平任务中从呈现刺激到被试按键反应的时间)与维度差异偏好的关系。2个反应时均进行对数转换。将PDD分数作为因变量, 分别将选择反应时和天平反应时作为固定效应做混合模型线性回归。结果发现: 选择反应时的回归系数显著为负,= −0.12, 95% CI = [−0.19, −0.06],= −3.70,< 0.001 (见图3a); 天平反应时的回归系数显著为负,= −0.12, 95% CI = [−0.19, −0.06],= −3.81,< 0.001 (见图3b), 结果支持了H2。 2.2.4 维度差异偏好与注视熵 为检验H3, 本研究考察了眼跳注视熵和静态注视熵指标与维度差异偏好的关系。被试的眼跳注视熵和静态注视熵的均值分别为0.66 (95% CI = [0.63, 0.69])和1.23 (95% CI = [1.20, 1.27])。将PDD分数作为因变量, 分别将眼跳注视熵和静态注视熵作为固定效应做混合模型线性回归。结果发现: 眼跳注视熵的回归系数显著为负,= −0.19, 95% CI = [−0.33, −0.05],= −2.71,= 0.007 (见图3c); 静态注视熵的回归系数显著为负,= −0.27, 95% CI = [−0.43, −0.10],= −3.17,= 0.002 (见图3d)。以上结果支持了H3。 2.2.5 维度差异判断与基于维度的注意分配 为考察基于维度的注意分配与维度差异判断的关系, 本研究采用结果维度注视比例(outcome gaze proportion)这一可反映维度注意分配的常用指标(Amasino et al., 2019; Ashby et al., 2018; Franco-Watkins et al., 2016; Zhou et al., 2021)。其计算公式如下: 该指标的取值范围为[−1, 1], 其值越大, 表示结果维度的相对注视时间越长。在本实验中, 被试的结果维度注视比例均值为−0.02 (95% CI = [−0.04, 0.01])。将DDJ分数作为因变量, 将结果维度注视比例作为固定效应做混合模型线性回归。结果发现: 结果维度注视比例的回归系数显著, b = 0.31, 95% CI = [0.21, 0.41], t = 5.96, p < 0.001, 如图3e所示, 这一结果支持了H4。 图3 实验1中(a)选择反应时与PDD分数的关系, (b)天平反应时与PDD分数的关系, (c)眼跳注视熵与PDD分数的关系, (d)静态注视熵与PDD分数的关系, (e)结果维度注视比例与DDJ分数的关系。 注: 红线为回归拟合线, 误差线为95%置信区间。 实验1发现, 反应时、注视熵等指标可显著预测维度差异偏好。实验2在实验1的基础上进行了改进, 以重复验证以上效应是否稳健。首先, 为验证实验1结果的稳健性, 实验2在实施前进行了备案(pre-register, 见https://osf.io/34c6x)。其次, 实验1所使用的跨期时间和金钱量级相对较小, 实验2将跨期选项的量级增大, 以验证所发现效应在相对较大量级的跨期决策中是否依然存在。第三, 为进一步验证维度差异偏好估计方式的有效性, 实验2要求被试重复2次相同的跨期选择, 以考察维度差异偏好与选择反转(choice reversal)的关系。以往研究发现, 偏好强度与选择反转相关(Alós-Ferrer & Garagnani, 2021)。偏好强度越大, 个体在随后相同的选择中改变选择(即选择反转)的可能性越低。按照相似的逻辑, 本研究假设, 维度差异偏好越大, 个体在随后相同的选择中出现选择反转的可能性越低。 3.1.1 被试 基于实验1中关于反应时、眼跳注视熵和静态注视熵等结果, 实验2采用R语言环境中的程序包计算所需样本量。采用混合模型线性回归, 设置统计检验力水平为1 − β = 0.95, α水平为0.05。计算所需样本量为= 51 (3360试次, 基于天平反应时的结果)。实验共招募59名大学生参与实验(平均年龄21.9 ± 2.1岁, 女性33人)。所有被试视力或矫正视力正常, 且实验前签署了知情同意书。实验结束后被试获得20元人民币的基本报酬。研究得到所在单位伦理委员会批准。 3.1.2 实验材料与实验程序 实验材料与实验1不同的是, 跨期选项的金钱结果与延迟时间的量级增大了。跨期选项的金钱设置4种固定金额: 20元, 50元, 100元和200元; 时间设置为4种固定延迟: 立即, 10天后, 50天后和100天后。将金钱与时间组合成36对无强占优的选项(见补充材料表S2, https://osf.io/xtbjk/)。 实验任务、流程与实验1基本相同。所不同的是, 在实验2中, 跨期选择任务包含2个组块, 每个组块包含的试次完全相同, 即36对选择重复2次, 以考察被试在2次相同的跨期选择中是否选择了不一致的选项(即出现选择反转)。此外, 由于金钱量级相对较大, 实验2修改了激励方式。在跨期选择任务开始前告知被试, 全部实验结束后, 随机选取某个被试的其中一次选择, 给予其额外奖励。这也是跨期决策研究中常用的激励方式(Reeck et al., 2017)。 实验总计4248试次, 其中1试次因眼动追踪失败而在数据分析时被剔除, 共计4247有效试次。 3.2.1 描述性统计 被试在跨期选择任务中选择LL选项比例的均值为50.0% (95% CI = [42.1%, 57.8%]), 平均反应时间为3.02 s (95% CI = [2.72, 3.31])。在模拟天平任务中的判断分数均值为3.74 (95% CI = [3.50, 3.98]), 平均反应时间为7.05 s (95% CI = [6.18, 7.93])。被试在选择任务中选择反转(即面对相同选项做出不一致选择)的比例为17.4% (95% CI = [14.7, 20.2])。 3.2.2 维度差异偏好与模拟天平分数 首先将被试的跨期选择作为因变量, 将模拟天平分数作为固定效应, 做混合模型逻辑回归。结果发现: 模拟天平分数可显著预测跨期选择,= 0.59, 95% CI = [0.54, 0.65], OR = 1.81,= 21.69,< 0.001, 如图4a所示, 这一结果与实验1相似。 其次考察维度差异判断与模拟天平分数的关系。将模拟天平分数作为因变量, 将DDJ分数作为固定效应做混合模型线性回归。结果发现, DDJ分数的回归系数显著,= 0.68, 95% CI = [0.64, 0.73],= 28.30,< 0.001, 如图4b所示。 最后考察维度差异偏好与天平判断强度的关系。将天平判断强度分数作为因变量, 将PDD分数作为固定效应做混合模型线性回归。结果发现, PDD分数的回归系数显著,= 0.26, 95% CI = [0.23, 0.29],= 16.21,< 0.001, 如图4c所示。 3.2.3 维度差异偏好与选择反转 将选择反转作为因变量(选择反转记为1, 未反转记为0), 分别将天平判断强度与第1次选择时(即第1组块的试次)的PDD分数作为固定效应, 做混合模型逻辑回归。结果发现: 天平判断强度可显著负向预测选择反转,= −0.33, 95% CI = [−0.46, −0.20], OR = 0.72,= −4.98,< 0.001, 如图5a所示。PDD分数亦可显著负向预测选择反转,= −0.17, 95% CI = [−0.29, −0.05], OR = 0.85,= −2.74,= 0.006, 如图5b所示。这一结果表明, 天平判断强度与维度差异偏好均可负向预测被试的选择反转行为, 从另一角度验证了本研究中维度差异偏好指标的有效性。 图4 实验2中(a) 模拟天平分数对跨期选择的预测效应, (b) DDJ分数与模拟天平分数的关系以及(c) PDD分数与天平判断强度的关系。注: 误差线为95%置信区间。 图5 实验2中(a) 天平判断强度和(b) 维度差异偏好(PDD分数)对选择反转的预测效应。误差线表示95%置信区间。 图6 实验2中(a) 选择反应时与PDD分数的关系, (b) 天平反应时与PDD分数的关系, (c) 眼跳注视熵与PDD分数的关系, (d) 静态注视熵与PDD分数的关系, (e) 结果维度注视比例与DDJ分数的关系。 注: 红线为回归拟合线, 误差线为95%置信区间。 3.2.4 维度差异偏好与反应时 将PDD分数作为因变量, 分别将选择反应时和天平反应时作为固定效应做混合模型线性回归。结果发现: 选择反应时的回归系数显著为负,= −0.28, 95% CI = [−0.34, −0.22],= −9.98,< 0.001; 天平反应时的回归系数显著为负,= −0.17, 95% CI = [−0.22, −0.12],= −6.89,< 0.001, 如图6a和6b所示。该结果与实验1相似, 支持了H2。 3.2.5 维度差异偏好与注视熵 被试的眼跳注视熵和静态注视熵的均值分别为0.63 (95% CI = [0.59, 0.66])和1.19 (95% CI = [1.16, 1.23])。将PDD分数作为因变量, 将眼跳注视熵和静态注视熵分别作为固定效应做混合模型线性回归。结果发现: 眼跳注视熵的回归系数显著为负,= −0.41, 95% CI = [−0.53, −0.29],= −6.77,< 0.001; 静态注视熵的回归系数显著为负,= −0.50, 95% CI = [−0.64, −0.37],= −7.78,< 0.001, 如图6c和6d所示。该结果与实验1相似, 支持了H3。 3.2.6 维度差异判断与基于维度的注意分配 被试的结果维度注视比例均值为−0.06 (95% CI = [−0.09, −0.03])。与实验1相似, 将DDJ分数作为因变量, 将结果维度注视比例作为固定效应做混合模型线性回归。结果发现: 结果维度注视比例的回归系数显著,= 0.27, 95% CI = [0.18, 0.35],= 6.11,< 0.001, 如图6e所示。 本研究通过2个眼动实验, 检验了相关眼动指标对维度差异偏好的预测作用, 为基于维度的跨期模型提供了更直接的过程证据。研究结果发现: 基于权衡模型拟合的维度差异偏好与模拟天平任务的维度差异判断显著相关(实验1), 且能够负向预测随后的选择反转(实验2), 验证了维度差异偏好估计方式的有效性。本研究进一步发现: 反应时、眼跳注视熵、静态注视熵等指标均与维度差异偏好负相关, 结果维度注视比例与维度差异判断正相关, 这些结果为跨期决策中维度间差异比较的心理机制提供了证据支持。本研究通过2个实验验证了以上结果的稳健性, 为基于维度的跨期模型提供了更直接的过程支持证据。 本研究验证了一种估计维度差异偏好的有效方法。对于主观维度差异的测量, 以往研究多采用直观模拟天平任务(江程铭等, 2016; 蒋元萍等, 2022)。虽然该范式具有直观易懂的优点, 但需要在决策前或决策后额外测量被试的主观维度差异判断。本研究所提出的维度差异偏好的估计方法完全基于个体的跨期选择, 无需额外测量数据即可进行估计, 简单便捷, 亦可应用于纸笔问卷测验中。而且, 这一测量方式更适用于定量的数理模型建构, 具有其独特优势。 我们认为, 相比于跨期决策行为结果, 维度差异偏好指标的优点有三。第一, 维度差异偏好可更精细地揭示个体的耐心程度。即使二人的跨期选择相同, 若维度差异判断不同, 其耐心程度也可能存在差异, 在随后的跨期选择中也可能表现出不同的时间偏好模式。第二, 维度差异偏好可预测选择反转。类似于决策信心, 偏好强度的强弱往往能预测个体在随后决策中的选择反转(Alós-Ferrer & Garagnani, 2021; Moran et al., 2015)。本研究发现, 维度差异偏好也可负向预测选择反转, 维度差异偏好越低, 个体在随后面临相同选择时越可能做出不同选择。换句话说, 研究者可借助维度差异偏好这一指标, 在一定程度上实现预测个体未来跨期决策行为的目标。同时, 也有学者认为, 选择反转意味着决策误差(choice error) (Konovalov & Krajbich, 2019), 因此维度差异偏好也可在一定程度上作为衡量决策误差的指标。第三, 当跨期决策结果不明确时, 亦可通过反映维度差异偏好的相关指标来间接推断选择。以反应时为例, 假如我们无法得知张三在“1年后获得1000元”还是“3年后获得1200元”以及“1年后获得1000元”还是“3年后获得1500元”两个跨期选择中的选择结果。但我们知道他在前者上花了5 s的时间做出选择, 而在后者上花了4 s的时间做出选择。反应时可反映其维度差异偏好, 因此可推断, 当增大结果维度的差异后, 张三的维度差异偏好也随之增大, 这表明其在第1次选择中认为结果维度的差异较大, 可断定其会选择LL选项。由此可见, 通过比较2次选择的反应时的变化, 我们即可推定其选择行为。 本研究为维度差异偏好与信息加工过程的关系提供了启示。近年来, 一些研究者尝试将顺序抽样模型的理论框架与基于维度的跨期模型相结合, 将跨期决策描述为在结果与延迟维度间累积证据的信息加工过程, 并验证这些模型对选择和反应时的解释力(Amasino et al., 2019; Dai & Busemeyer, 2014; Dai et al., 2018)。然而据我们所知, 尚没有研究尝试发展结合眼动注视的跨期模型。本研究提出iaDDM的理论框架, 假设决策者基于眼动注视对两维度的累积证据差值可反映其维度差异偏好, 并发现反应时、注视熵等指标均与维度差异偏好相关。这些证据表明, 用iaDDM的框架去解释跨期决策中基于维度的信息加工过程是可行的。相比于用反应时等行为数据去拟合DDM, 发展基于眼动注视的DDM可帮助我们更好地理解个体在决策时的信息加工过程, 且可以用更直接的过程证据去验证。 未来研究在定量发展iaDDM模型时应当注意4点。第一, 应当注意选择合适的理论内核。本研究基于权衡模型(Scholten & Read, 2010)来估计个体的维度差异偏好, 而尚存在其他基于维度的跨期模型, 如相似性模型(Leland, 2002)、齐当别抉择模型(Li, 2004, 2016)等。这些模型虽然基本内核相同, 但在效用函数等数学表达上尚存差异。未来研究在发展模型时应当注意比较鉴别不同模型的解释力。第二, 未来研究在发展模型时除了应注意模型对跨期选择的解释力外, 在模拟(simulation)数据时亦需慎重考虑该模型是否能复刻本研究所发现的关于维度差异偏好与眼动指标的数据模式。第三, 相比于单选项的双维度决策(Sullivan & Huettel, 2021), 双选项、双维度的跨期决策在构建眼动模型时应当注意证据累积的方向。举例来说, 当个体注视SS选项的结果信息时, 一些研究者认为这会增加对结果维度的累积证据(Gluth et al., 2020), 但也有研究者认为这会降低结果维度的累积证据, 因为SS选项的结果信息属于结果维度的缺点(Amasino et al., 2019), 这需要未来研究者进一步辨别与检验。第四, 虽然本研究结果支持了基于维度的跨期模型, 但并不能表明跨期决策中不存在基于选项的信息加工方式。事实上, 一些研究者用基于选项的双曲线折扣模型结合DDM来拟合反应时数据, 亦得到了证据支持(Konovalov & Krajbich, 2019; Rodriguez et al., 2014)。 本研究发现了注视熵与维度差异偏好的关系, 提示了注视熵在决策研究中的应用价值。作为整合性眼动指标, 注视熵通常用于衡量视觉搜索的复杂性(Krejtz et al., 2014; Schieber & Gilland, 2008)。其中, 眼跳注视熵衡量的是兴趣区之间随机眼跳的频繁程度, 它反映了信息搜索的效率(Shiferaw et al., 2019); 静态注视熵衡量的是不同兴趣区之间注视分布的均匀程度(Krejtz et al., 2014), 它反映了信息搜索的分布情况。以往研究多用注视熵指标来考察应用场景的眼动注视特点, 如研究者发现眼跳注视熵与医生所进行的外科手术场景的难度相关(di Stasi et al., 2016), 静态注视熵与模拟驾驶场景中的车道偏离情况相关(Shiferaw et al., 2018)。本研究首次将注视熵用于决策研究中, 以考察决策的认知加工过程, 未来研究亦可将其用于其他决策研究中。例如, 未来研究可用眼跳注视熵考察决策过程的复杂性, 以区分基于直觉的启发式策略与基于理性的分析式策略(Kahneman & Frederick, 2002)。又如, 以往研究使用不同维度的注视时间比例来衡量个体对选项信息的注视均匀程度(Su et al., 2013), 相比而言, 静态注视熵可对注视均匀程度提供更精确的整体性评估。此外, 考察两种注视熵的共变情况亦可帮助区分决策中的两种认知加工模式。有研究者提出, 静态注视熵的增大伴随眼跳注视熵的增大可能反映了眼动注视受到了自上而下的加工的影响; 相反, 静态注视熵的增大伴随眼跳注视熵的减小往往意味着更多自下而上的眼动控制(Shiferaw et al., 2019)。这一研究思路亦可用于决策研究中, 以帮助检验眼动注视与决策行为之间的因果关系(Liu, Lyu, et al., 2021; Liu et al., 2020)。 本研究验证了结果维度注视比例与维度差异判断的关系, 为这一指标在跨期决策中的进一步应用提供了新的参考证据。以往研究已经建立了结果维度的相对注视时间与决策者耐心程度的关系。例如, Amasino等(2019)发现, 结果维度的相对注视优势可预测个体的时间折扣率。又如, Liu, Lyu等(2021)发现, 当注视结果维度较多时, 个体更可能选择结果维度占优的LL选项, 反之亦然。然而, 当用结果维度的相对注视优势去预测选择时, 并未发现显著的预测效应。结合本研究发现, 我们推测, 个体的跨期决策存在诸多误差和噪声, 不易被注意分配等定量眼动指标所捕获, 而本研究所估计的维度差异判断是基于整体决策拟合而来, 可在一定程度上分离决策误差, 从而更精准地反映于注意分配等眼动指标上。这提示, 未来研究若聚焦于基于注视时长的眼动指标与跨期决策行为的关系, 应当注意决策误差的混淆作用, 避免错误解读阴性结果。 决策的眼动研究的目的之一是“读心”, 即基于决策者的眼动轨迹来预测其选择(Brandstätter & Körner, 2014; Stewart et al., 2015)。研究者期冀达到“我看你的眼睛在看什么就知道你想选什么”的效果。在基于维度的跨期决策理论框架下, 本研究结果暗示, 通过眼动数据我们不仅可断定个体判断哪个维度差异较大、从而选择何选项, 还可以断定个体判断两维度的差异究竟有多大, 对选项的偏好程度究竟有多强。换句话说, 通过眼动数据, 我们不仅可以知道你想选哪个选项, 还知道你有多想选那个选项。 本文通过2个实验考察了跨期决策中的维度差异偏好与信息加工过程的关系, 得出如下结论: (1) 基于权衡模型可有效估计个体在跨期决策时的维度差异偏好。(2) 反应时与维度差异偏好负相关。(3) 眼跳注视熵和静态注视熵与维度差异偏好负相关。(4) 基于维度的注意分配与维度差异判断正相关。 Ainslie, G. (1975). Specious reward: A behavioral theory of impulsiveness and impulse control.(4), 463−496. Alós-Ferrer, C., & Garagnani, M. (2021). Choice consistency and strength of preference., 109672. Amasino, D. R., Sullivan, N. J., Kranton, R. E., & Huettel, S. A. (2019). Amount and time exert independent influences onintertemporal choice.(4), 383−392. Arieli, A., Ben-Ami, Y., & Rubinstein, A. (2011). Tracking decision makers under uncertainty., 68−76. Ashby, N. J. S., Yechiam, E., & Ben-Eliezer, D. (2018). The consistency of visual attention to losses and loss sensitivity across valuation and choice.(12), 1791−1809. Baayen, R. H., Davidson, D. J., & Bates, D. M. (2008). Mixed- effects modeling with crossed random effects for subjects and items.(4), 390−412. Bates, D., Maechler, M., Bolker, B., & Walker, S. (2015). Lme4: Linear mixed-effects models using Eigen and S4.1−9. Retrieved from http://CRAN.R-project.org/ package=lme4. Brandstätter, E., & Körner, C. (2014). Attention in risky choice., 166−176. Brysbaert, M., & Stevens, M. (2018). Power analysis and effect size in mixed effects models: A tutorial.1(1), Article 9. Cheng, J., & González-Vallejo, C. (2016). Attribute-wise vs. alternative-wise mechanism in intertemporal choice: Testingthe proportional difference, trade-off, and hyperbolic models.(3), 190−215. Cuve, H. C., Castiello, S., Shiferaw, B., Ichijo, E., Catmur, C., &Bird, G. (2021). Alexithymia explains atypical spatiotemporal dynamics of eye gaze in autism., 104710. Dai, J., & Busemeyer, J. R. (2014). A probabilistic, dynamic, and attribute-wise model of intertemporal choice.(4), 1489−1514. Dai, J., Pleskac, T. J., & Pachur, T. (2018). Dynamic cognitive models of intertemporal choice., 29−56. De Martino, B., Fleming, S. M., Garrett, N., & Dolan, R. J. (2013). Confidence in value-based choice.(1), 105−110. Diederich, A. (2003). MDFT account of decision making under time pressure.(1), 157−166. Di Stasi, L. L., Diaz-Piedra, C., Rieiro, H., Sanchez Carrion, J. M., Martin Berrido, M., Olivares, G., & Catena, A. (2016). Gaze entropy reflects surgical task load.(11), 5034−5043. Ericson, K. M. M., White, J. M., Laibson, D., & Cohen, J. D. (2015). Money earlier or later? Simple heuristics explain intertemporal choices better than delay discounting does.(6), 826−833. Fisher, G. (2021). Intertemporal choices are causally influenced by fluctuations in visual attention.(8), 4961−4981. Franco-Watkins, A. M., Mattson, R. E., & Jackson, M. D. (2016). Now or later? Attentional processing and intertemporal choice.(2−3), 206−217. Frederick, S., Loewenstein, G., & O’donoghue, T. (2002). Time discounting and time preference: A critical review.(2), 351−401. Gluth, S., Kern, N., Kortmann, M., & Vitali, C. L. (2020). Value-based attention but not divisive normalization influencesdecisions with multiple alternatives.(6), 634−645. He, G., Chen, H., Lin, J. (2009). Psychological mechanisms for anomolies in intertemporal choice.(4), 298−305. [何贵兵, 陈海贤, 林静. (2009). 跨期选择中的反常现象及其心理机制.(4), 298−305.] Jiang, C. M., Liu, H. Z., Cai, X. H., & Li, S. (2016). A process test of priority models of intertemporal choice.(1), 59−72. [江程铭, 刘洪志, 蔡晓红, 李纾. (2016). 跨期选择单维占优模型的过程检验.(1), 59−72.] Jiang, Y., Jiang, C., Hu, T., & Sun, H. (2022). Effects of emotion on intertemporal decision-making: Explanation from the single dimension priority model.(2), 122−140. [蒋元萍, 江程铭, 胡天翊, 孙红月. (2022). 情绪对跨期决策的影响: 来自单维占优模型的解释.(2), 122−140.] Judd, C. M., Westfall, J., & Kenny, D. A. (2012). Treating stimuli as a random factor in social psychology: A new and comprehensive solution to a pervasive but largely ignored problem.(1), 54−69. Kahneman, D., & Frederick, S. (2002). Representativeness revisited: Attribute substitution in intuitive judgment. In T. Gilovich, D. Griffin, & D. Kahneman (Eds.),(pp. 49−81). Cambridge UK: Cambridge University Press. Konovalov, A., & Krajbich, I. (2019). Revealed strength of preference: Inference from response times.(4), 381−394. Krajbich, I., Armel, C., & Rangel, A. (2010). Visual fixations and the computation and comparison of value in simple choice.(10), 1292−1298. Krajbich, I., Lu, D., Camerer, C., & Rangel, A. (2012). The attentional drift-diffusion model extends to simple purchasing decisions., 193. Krajbich, I., & Rangel, A. (2011). Multialternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based decisions.(33), 13852−13857. Krejtz, K., Szmidt, T., Duchowski, A. T., & Krejtz, I. (2014). Entropy-based statistical analysis of eye movement transitions.(pp.159−166). https://doi.org/ 10.1145/2578153.2578176 Kuznetsova, A., Brockhoff, P. B., & Christensen, R. H. B. (2017). lmerTest package: Tests in linear mixed effects models.(13), 1−26. Laibson, D. (1997). Golden eggs and hyperbolic discounting.(2), 443−478. Leland, J. W. (2002). Similarity judgments and anomalies in intertemporal choice.(4), 574−581. Li, S. (2004). A behavioral choice model when computational ability matters., 147−163. Li, S. (2016).. Shanghai, China: East China Normal University Press. Liang, Z. Y., & Liu, H. (2011). Exploring the nature of intertemporal choice.(7), 959−966. [梁竹苑, 刘欢. (2011). 跨期选择的性质探索.(7), 959−966.] Liu, H. Z., Jiang, C. M., Rao, L. L., & Li, S. (2015). Discounting or priority: Which rule dominates the intertemporal choice process?(4), 522−532. [刘洪志, 江程铭, 饶俪琳, 李纾. (2015). “时间折扣”还是“单维占优”?——跨期决策的心理机制.(4), 522−532.] Liu, H. Z., Lyu, X. K., Wei, Z. H., Mo, W. L., Luo, J. R., & Su, X. Y. (2021). Exploiting the dynamics of eye gaze to bias intertemporal choice.(3), 419−431. Liu, H. Z., Wei, Z. H., & Li, P. (2021). Influence of the manner of information presentation on risky choice., 650206. Liu, H. Z., Zhou, Y. B., Wei, Z. H., & Jiang, C. M. (2020). The power of last fixation: Biasing simple choices by gaze- contingent manipulation., 103106. Loewenstein, G., & Prelec, D. (1992). Anomalies in intertemporal choice: Evidence and an interpretation.(2), 573−597. Moran, R., Teodorescu, A. R., & Usher, M. (2015). Post choice information integration as a causal determinant of confidence:Novel data and a computational account., 99−147. Read, D. (2001). Is time-discounting hyperbolic or subadditive?(1), 5−32. Read, D., & Scholten, M. (2012). Tradeoffs between sequences: Weighing accumulated outcomes against outcome-adjusted delays.(6), 1675−1688. Reeck, C., Wall, D., & Johnson, E. J. (2017). Search predicts and changes patience in intertemporal choice.(45), 11890−11895. Rodriguez, C. A., Turner, B. M., & McClure, S. M. (2014). Intertemporal choice as discounted value accumulation.(2), e90138. Samuelson, P. A. (1937). A note on measurement of utility.(2), 155−161. Scholten, M., & Read, D. (2006). Discounting by intervals: A generalized model of intertemporal choice.(9), 1424−1436. Scholten, M., & Read, D. (2010). The psychology of intertemporal tradeoffs.(3), 925−944. Shannon, C. E. (1948). A mathematical theory of communication.(3), 379−423. Shiferaw, B., Downey, L., & Crewther, D. (2019). A review of gaze entropy as a measure of visual scanning efficiency., 353−366. Shiferaw, B. A., Downey, L. A., Westlake, J., Stevens, B., Rajaratnam, S. M. W., Berlowitz, D. J., … Howard, M. E. (2018). Stationary gaze entropy predicts lane departure events in sleep-deprived drivers.(1), 2220. Stewart, N., Hermens, F., & Matthews, W. J. (2015). Eye movements in risky choice.(2−3), 116−136. Su, Y., Rao, L. L., Sun, H. Y., Du, X. L., Li, X., & Li, S. (2013). Is making a risky choice based on a weighting and adding process? An eye-tracking investigation.(6), 1765−1780. Sui, X. Y., Liu, H. Z., & Rao, L. L. (2020). The timing of gaze-contingent decision prompts influences risky choice., 104077. Sullivan, N. J., & Huettel, S. A. (2021). Healthful choices depend on the latency and rate of information accumulation.(12), 1698−1706. Tversky, A., & Shafir, E. (1992). Choice under conflict: The dynamics of deferred decision.(6), 358−361. Wei, Z. H., & Li, X. (2015). Decision process tracing: Evidencefrom eye-movement data.(12), 2029−2041. [魏子晗, 李兴珊. (2015). 决策过程的追踪: 基于眼动的证据.(12), 2029−2041.] Preference of dimension-based difference in intertemporal choice: Eye-tracking evidence LIU Hong-Zhi4,5, YANG Xing-Lan4, LI Qiu-Yue4, WEI Zi-Han1,2,3 (1Faculty of Psychology, Tianjin Normal University, Tianjin 300387, China) (2Key Research Base of Humanities and Social Sciences of the Ministry of Education, Academy of Psychology and Behavior, Tianjin Normal University, Tianjin 300387, China) (3Tianjin Social Science Laboratory of Students’ Mental Development and Learning, Tianjin 300387, China) (4Department of Social Psychology, Zhou Enlai School of Government, Nankai University, Tianjin 300350, China) (5Laboratory of Behavioral Economics and Policy Simulation, Nankai University, Tianjin 300071, China) Intertemporal choice is an important and ubiquitous concept that refers to decisions involving tradeoffs among outcomes at different points of time. It is not only a unique feature of human behavior but also relevant to policymaking and national welfare. Dimension-based models, such as tradeoff model, equate-to-differentiate theory, and similarity model, assume that individuals tend to compare the difference between dimensions of delay and outcome before deciding on a single dimension when choosing between a smaller-sooner option and a larger-later one. Considerable empirical evidence from behavioral and process data supports the use of dimension-based models. The existing dimension-based models provide qualitative explanations for an individual’s intertemporal choice and focus on “which dimension is the greater difference dimension”, but ignore the preference of dimension-based difference (i.e., “how much different of the difference between the two dimensions”). In the present study, we used eye-tracking technology to examine the relationship between the preference of dimension-based difference, which is estimated by the tradeoff model, and the information searching process, which is reflected by eye-tracking measures. Two experiments were conducted to test the hypotheses. A total of 75 college students (61 females; mean age = 20.9 ± 2.4 years) participated in Experiment 1. Participants were told to complete two tasks. In the intertemporal choice task, participants chose their preferred option between the two intertemporal options, and their eye movements were recorded in the task. In the analogue scale task, participants were asked to indicate their subjective dimension-based difference judgment by using numbers 1~7. In Experiment 2, we recruited 59 college students (33 females; mean age = 21.9 ± 2.1 years) to participate in the experiment. The tasks and procedures were similar to Experiment 1 except that the participants were asked to repeat the intertemporal choice task twice. The results indicated that preference of dimension-based difference (PDD), which is estimated by the tradeoff model, correlated with the subjective dimension-based difference judgment measured by the analogue scale task (Experiment 1) and could negatively predict the choice reversals (Experiment 2). These findings proved the validity of the estimation of PDD. The results in the two experiments consistently revealed that decision time, gaze transition entropy (a measure of visual scanning efficiency), and stationary gaze entropy (a measure of the level of even distribution across different areas of interest) could negatively predict the PDD, indicating that the information searching process during intertemporal choice could reflect the preference of dimension-based difference. We also found that the outcome gaze proportion (a measure of attention allocation) could predict the dimension-based difference judgment, which is consistent with previous research. Our findings proved the validity of the estimation method of PDD, which could quantitatively estimate the PDD when making an intertemporal choice based on their choices without extra inquiry. The current research highlighted the correlation between the preference of dimension-based difference and the information searching process, providing further process evidence for dimension-based intertemporal models. Future studies that focus on developing intertemporal models involving eye movements should consider replicating the pattern between PDD and eye-tracking measures as revealed in the present study when running data simulations. Our findings also suggest that compared to the determinant models, the probabilistic models can better describe an individual’s intertemporal choice, thereby highlighting the direction of the development of intertemporal models. intertemporal choice, dimension-based intertemporal models, preference of dimension-based difference, eye-tracking technique 2022-01-18 * 国家自然科学基金项目(71901126, 72001158), 教育部人文社会科学研究青年项目(19YJC190013)和中央高校基本科研业务费专项资金(63222045)资助。 魏子晗, E-mail: weizihan@tjnu.edu.cn B849: C91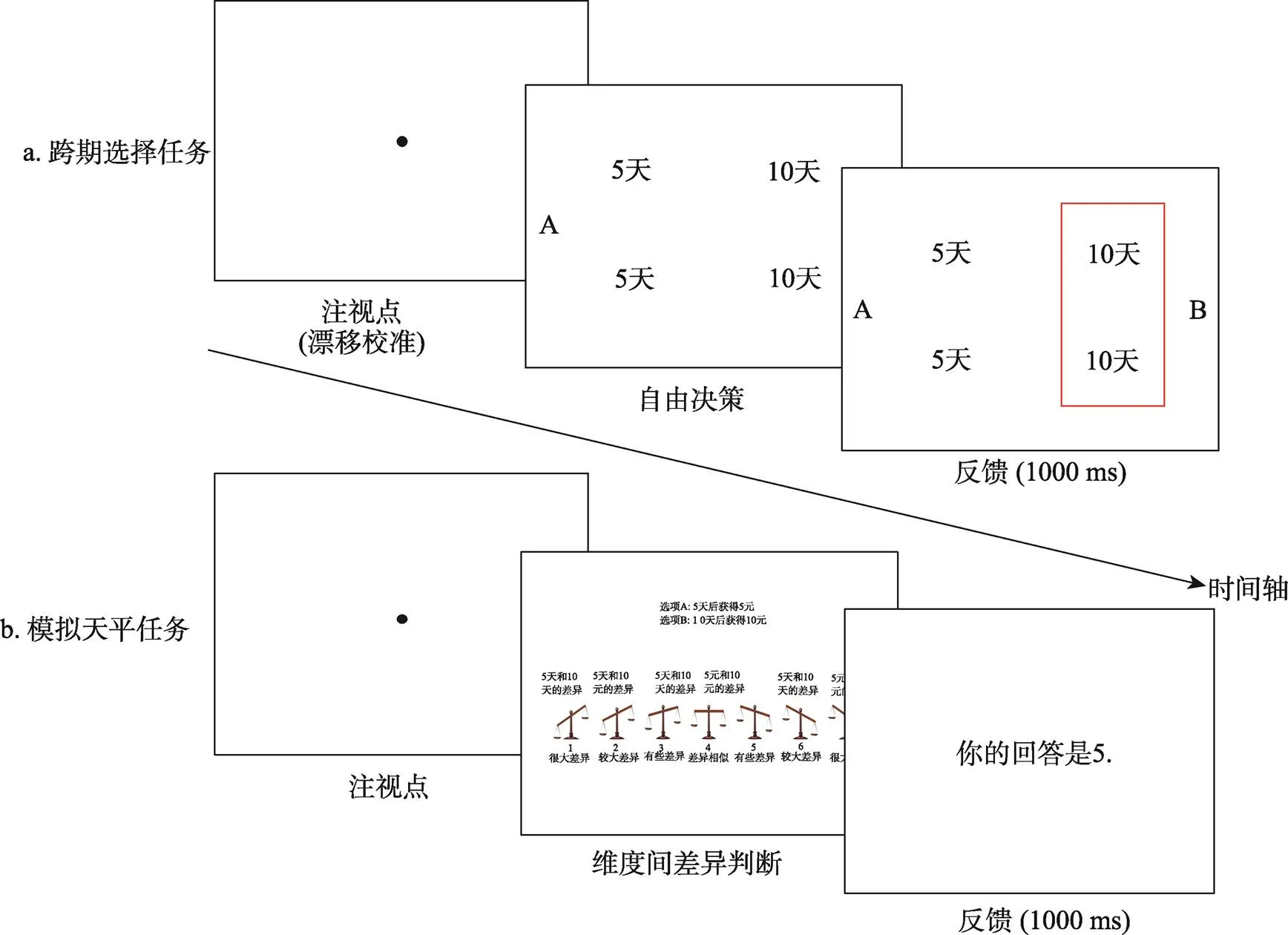
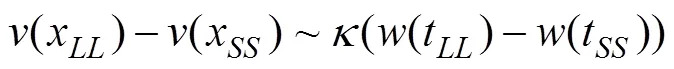
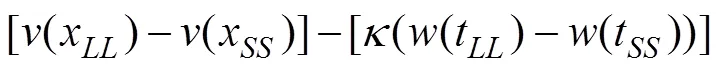
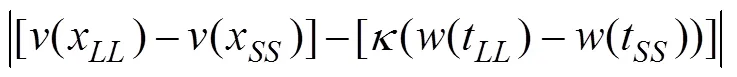
2.2 结果


3 实验2:重复验证并检验维度差异偏好与选择反转的关系
3.1 方法
3.2 结果

4 讨论
4.1 维度差异偏好的优点
4.2 基于维度的信息加工与维度差异偏好
4.3 相关眼动指标在决策研究中的应用
5 结论

