适用于凸曲线轮廓数据的平滑处理方法

李建鑫 陈 鸿 王晋祺

1(新疆政法学院 新疆 图木舒克 844000) 2(中北大学仪器与电子学院 山西 太原 030051) 3(上海无线电设备研究所 上海 201109)

0 引 言

随着经济的发展与人力成本的提高,在眼镜片的加工过程中对自动化程度的要求越来越高。为了适应市场需求,中北大学推出了眼镜片自动磨边机系统,此系统采用了基于机器视觉的轮廓提取系统提取眼镜片的轮廓数据[1]。为了便于后续依照轮廓数据的磨削加工,需要对轮廓提取系统所采集的眼镜片轮廓数据加以平滑处理。探求一种专门适用于眼镜片轮廓数据的平滑处理方法是提高眼镜片自动磨边机系统加工精度的关键。

目前,对数据的平滑处理多采用数值分析的方法。常见的有滑动平均法、Savitzky-Golay卷积平滑法、高斯尺度变换法[2-3]等,通常会针对应用场景灵活组合,多次平滑。例如:文献[4]组合使用滑动平均法、Savitzky-Golay卷积平滑法多次平滑以处理线结构光中心线提取问题;文献[5]组合使用滑动平均法、Savitzky-Golay卷积平滑法、高斯尺度变换法多次平滑以处理车轮实测型面数据平滑问题。平滑几次之后结束通常是根据经验设定[4]或者以平滑误差的标准差为条件[5]。

然而针对眼镜片轮廓数据的平滑处理,为了防止在后续依照轮廓数据的磨削加工中产生过切,应当以得到全凸的光滑曲线作为平滑结束的条件。本文将此类以得到全凸的光滑曲线为目的的平滑称为保凸平滑。传统的平滑处理方法如果以得到全凸的光滑曲线作为平滑结束的条件,往往会平滑次数过多,造成耗时过长且严重丢失数据的细节。

本文提出一种专门适用于眼镜片轮廓这一类凸曲线数据的保凸平滑的方法:寻找特征将采集到的轮廓数据分为可靠点和噪点两种类型,剔除噪点后,对可靠点进行基于Bézier曲线的保形插值来补全轮廓。

1 平滑处理目的是避免磨削过切

眼镜片的轮廓线在理想中为光滑的全凸闭合曲线,如图1所示。

图1 理想中的眼镜片轮廓曲线

然而由于测量系统的误差、测量环境等的影响,必然会使测量得到的轮廓数据中包含大量的噪声干扰,根据实测数据绘制的眼镜片轮廓如图2所示。

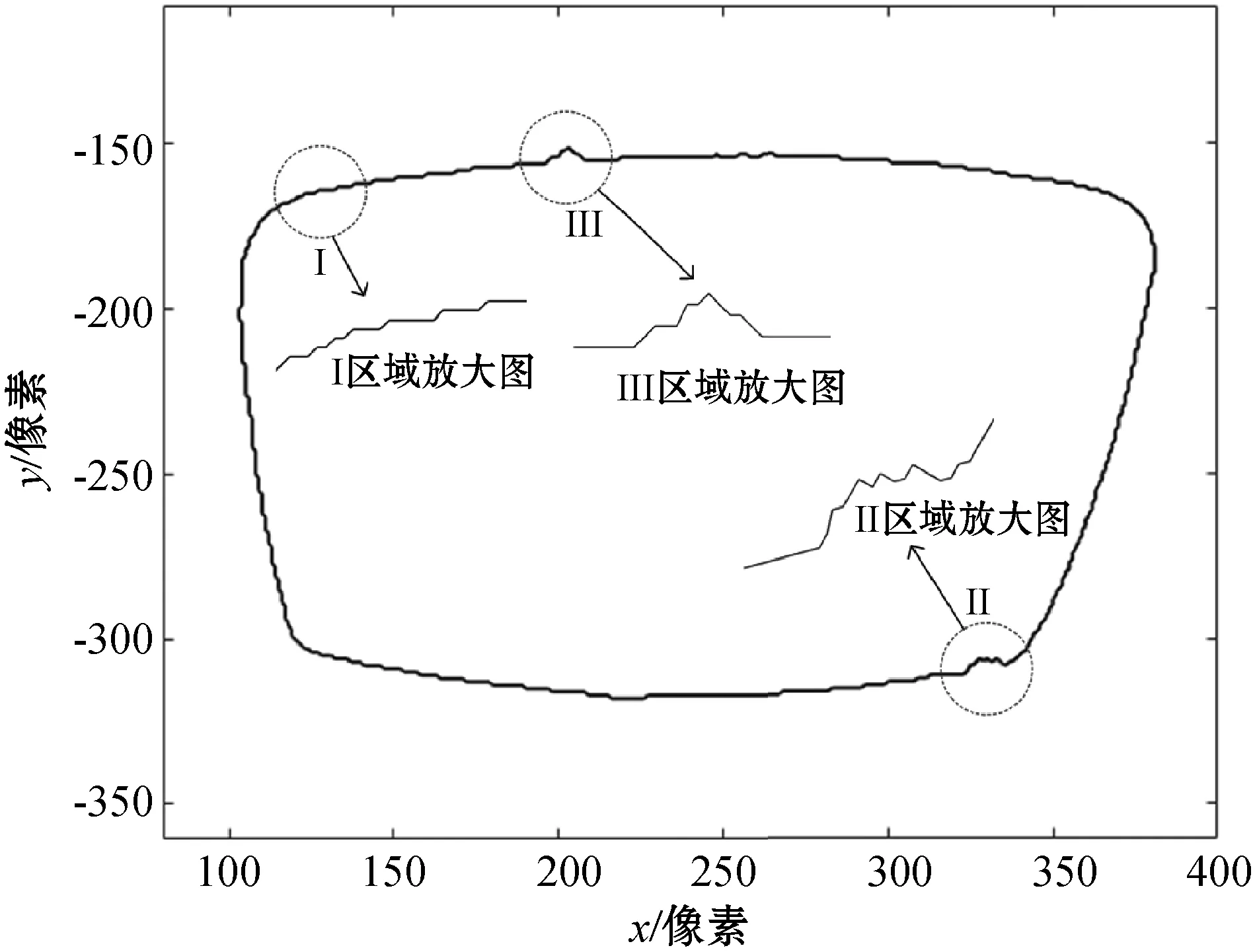
图2 实测的眼镜片轮廓曲线

为了便于分析,本文将实测的轮廓曲线的数据点分为可靠点和噪点两种类型,并将噪点依照特征再次细分。图2中I区域的锯齿形信号,是由测量系统的误差引起的,本文将此类噪点称为I型噪点。图2中II区域内轮廓上凹陷的部分,是由测量环境中的干扰光线引起,本文将此类噪点称为II型噪点。图2中III区域内轮廓上凸起的部分,是由测量光路中的污点导致的,本文将此类噪点称为III型噪点。其中:I型噪点是需要平滑处理的主要问题;II型噪点和III型噪点只是偶尔出现。

在采集到轮廓数据后,眼镜片自动磨边机系统会依据轮廓数据以磨削加工的方式加工眼镜片。磨削加工采用逐点磨削的方式,所用的磨轮半径较大,因此如果轮廓曲线上有凹陷的部分,磨削加工会造成对周围其他磨削点的过切[6],如图3所示,使磨削加工的结果和所给的轮廓数据极大偏差,磨削加工变得不可控,这是需要极力避免的,因此平滑处理首先要保证的是平滑处理后轮廓曲线是全凸的闭曲线,即为保凸平滑。

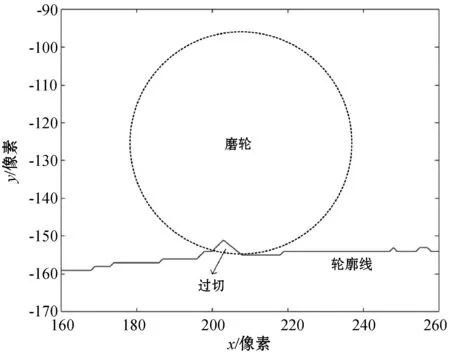
图3 过切示意图

2 可靠点和噪点的辨别

为了辨别噪点和可靠点,本文引入凸包算法,寻找轮廓数据的凸包,凸包是计算几何中的概念,若平面上包含有限个点的点集为Q,则其凸包是包含Q的最小凸多边形[7]。将凸包的顶点称为凸包点,凸包多边形的边称为凸包边。凸包算法的具体过程参考文献[8]。

利用凸包算法提取图2所示轮廓数据的凸包点并用叉号标记,结果如图4所示,将这些凸包点作为可靠点,其他点都作为噪点。可以看出对于I型噪点和II型噪点所在的区域,对可靠点和噪点的辨别效果很好,可是对于III型噪点所在的区域,对可靠点和噪点的辨别不准确。

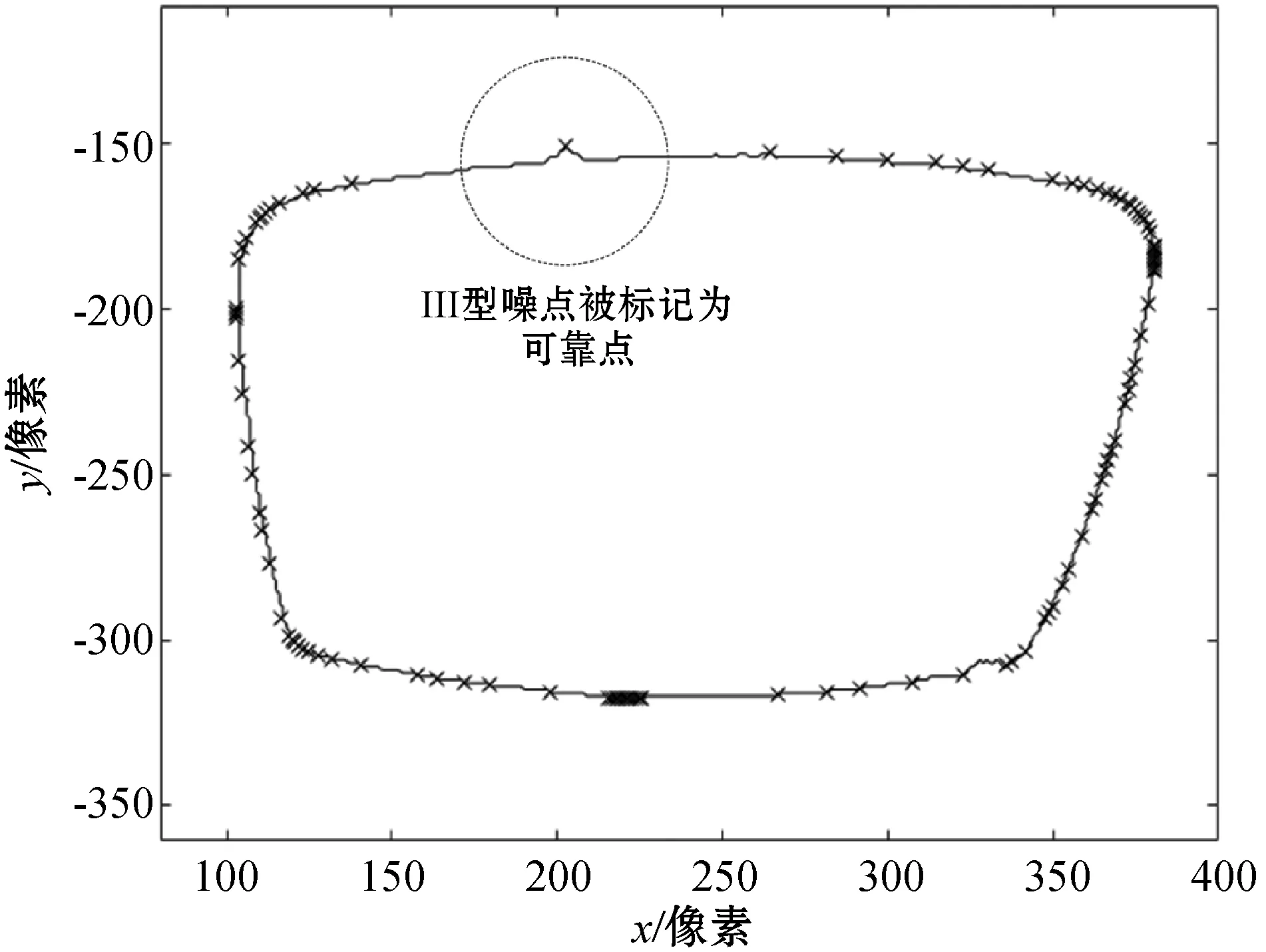
图4 凸包算法标记结果

为了实现对III型噪点的辨别,设计以下的方法。将相邻凸包点之间的轮廓点到这条凸包边的平均距离作为此凸包边的偏差。如果出现连续的偏差大于给定阈值的凸包边,则认为是受到III型噪点的影响,需要剔除III型噪点后重新辨别可靠点和噪点。如图5所示,凸包边AB、BC与轮廓点的偏差大于给定阈值,因此认为点B是III型噪点,且在点B的周围还存在其他III型噪点。

如图6所示,在点B右侧,依次将轮廓数据点Bri(i=0,1,…,n)与点A相连,如果点Bri与点A之间的轮廓点与直线ABri的平均距离大于给定阈值,则剔除掉Bri,直到符合阈值要求为止,这样就剔除掉了点B右侧的所有III型噪点。在点B左侧同理。

(a)

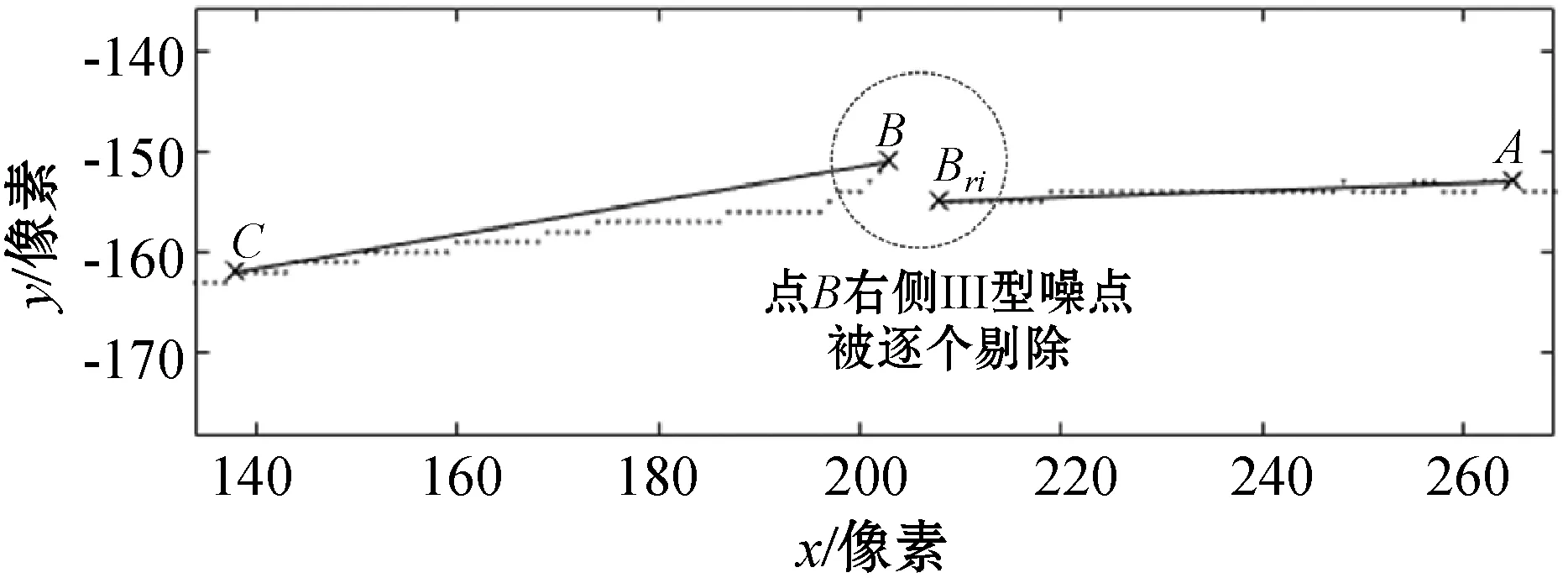
(b)图6 剔除点B右侧的III型噪点

剔除掉点B周围的III型噪点后,对剩下的所有轮廓点重新寻找凸包点。该方法可以解决偶尔出现的III型噪点问题。如图7所示,用叉号标记出来的是可靠点,对III型噪点辨别正确。

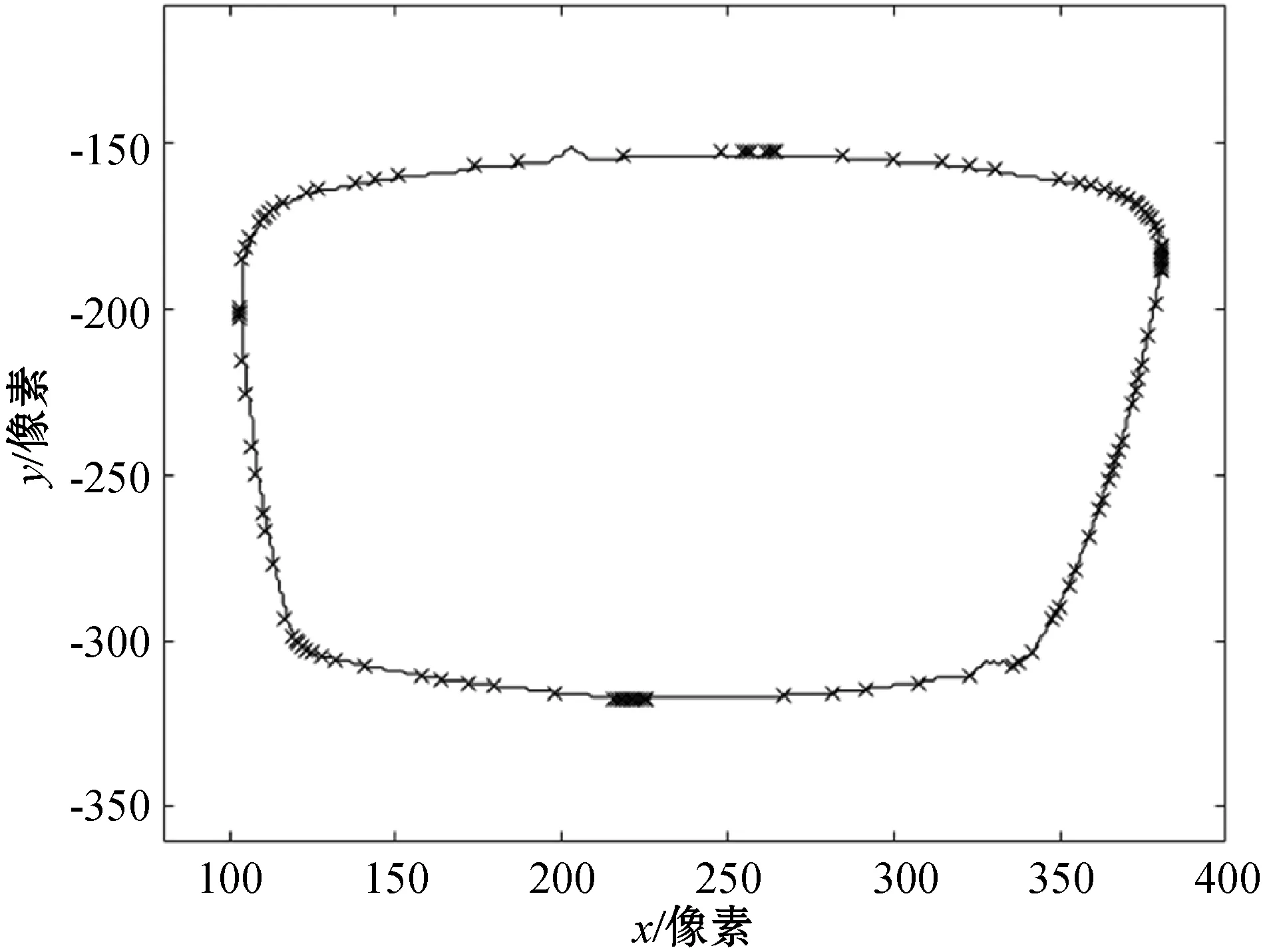
图7 正确辨别可靠点和噪点

3 方法设计

3.1 保凸插值简介

保凸插值是计算机图形学的重要研究内容。平面内的保凸插值是指构造一条平面曲线来通过平面内的单调凸点列,并与此点列的凸性保持一致[9]。对保凸插值方法的研究有许多成果,如:文献[10]提到的基于B样条曲线的保凸插值;文献[11-12]提到的基于权因子的NURBS曲线的保凸插值;文献[13-15]提到的基于三角样条曲线的保凸插值;文献[16]提到的保凸插值细分方法。然而这些方法往往运算量较大,如基于B样条曲线、三角样条曲线的保凸插值需要解一组限制了保凸条件和连续性条件的方程组[10-15];保凸插值细分方法需要独立判断每个细分点,同时极限曲线的连续性分析也是十分复杂[16]。

本文采用基于拼接三次Bézier曲线的保凸插值方法[17]。具体是在凸点列的每相邻两个凸点之间插入一条三次Bézier曲线。利用凸点列所连成的折线的运动方向来求插入的每段Bézier曲线合理的控制点。此方法避免了解方程组的运算,耗时少且在保证拼接的Bézier曲线之间G1连续的条件下,每相邻两个凸点之间的插值Bézier曲线有独立的形状调节参数。

3.2 Bézier曲线的数学表达式

一条平面内的Bézier曲线可以由给定平面中n+1个点的位置向量bi(i=0,1,…,n)来确定,Bézier曲线段的参数方程表示为[17]:

式中:bi(i=0,1,…,n)是Bézier曲线的控制点;Bi,n(t)表示的是Bernstein基函数。Bi,n(t)有以下形式:

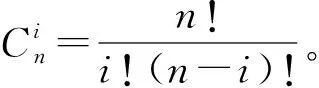
本文所使用的三次Bézier曲线参数公式展开为:

P(t)=b0(1-t)3+3b1t(1-t)2+

3b2t2(1-t)+b3t3t∈[0,1]

(3)

式中:bi(i=0,1,2,3)是三次Bézier曲线的四个控制点。

3.3 基于Bézier曲线的保形插值方法

本文使用拼接三次Bézier曲线保凸插值凸点列[17]。为了在凸点列的每相邻两个凸点之间插入一条三次Bézier曲线,需要在每相邻两个凸点之间插入两个新的控制点,且插入的控制点需要满足要求:插入控制点后新的点列依旧是凸点列。本文对插入的控制点的求取方法如下:

如图8所示,考虑凸点列中的任意四个相邻凸点Pi-1、Pi、Pi+1、Pi+2,作∠Pi-1PiPi+1的外角平分线与∠PiPi+1Pi+2的外角平分线交于点Oi。

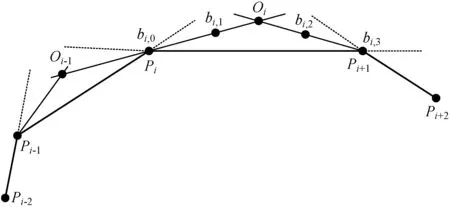
图8 Bézier曲线控制点的构造

在点Pi、Pi+1之间插入的三次Bézier曲线的控制点如下:

式中:λi、μi(0<λi,μi<1)是调节形状的参数,可以对整体的拼接Bézier曲线作局部调节。根据构造过程可以得知,所插入的每段Bézier曲线的控制点序列是凸的,因此插入的Bézier曲线是凸曲线。同样由构造控制点的过程可知每相邻两段Bézier曲线在拼接处的控制点三点共线,因此总体的拼接Bézier曲线满足G1连续[18],这样整体的拼接Bézier曲线是保凸的。

3.4 眼镜片轮廓的保形插值

剔除噪点之后的眼镜片轮廓如图9所示,对剩余可靠点的保形插值结果如图10所示。

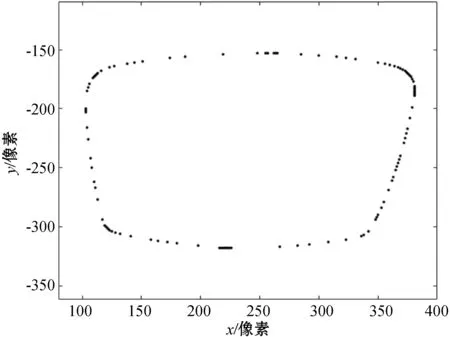
图9 剔除噪点后的轮廓

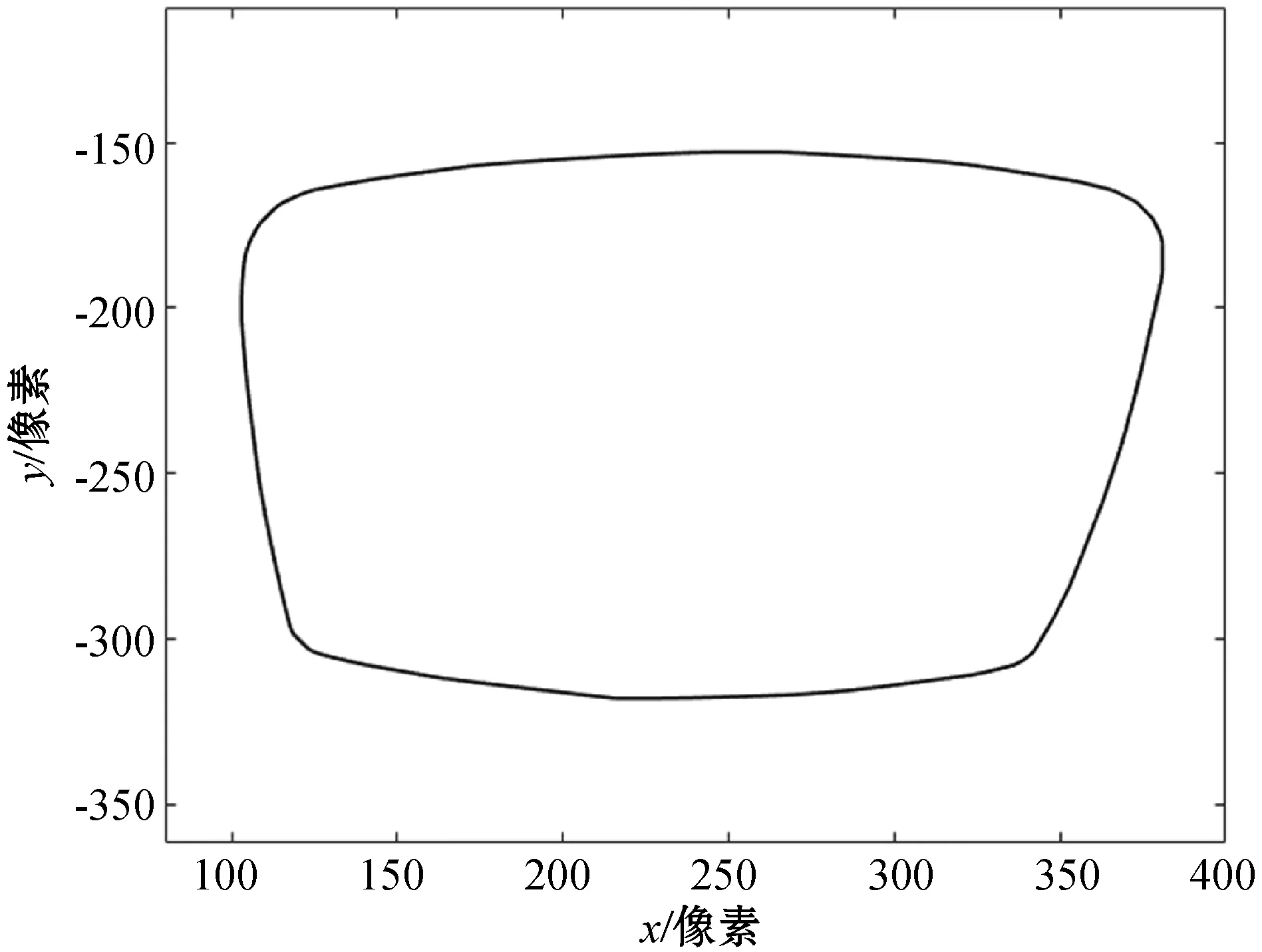
图10 对可靠点插值后的轮廓线

4 平滑处理的效果分析

将基于机器视觉的轮廓提取系统实测的眼镜片轮廓数据用本文方法进行处理,与滑动平均法、Savitzky-Golay卷积平滑法[2-5]的处理结果进行比较。图11-图13是三种方法的平滑效果,其中:虚线是平滑处理前的轮廓曲线;实线是平滑处理后的轮廓曲线。

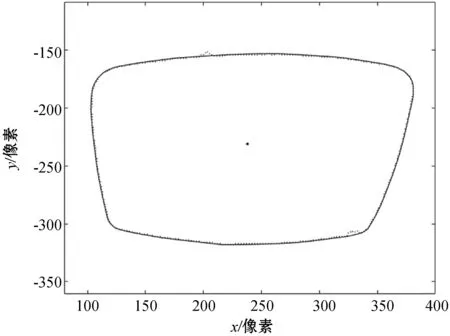
图11 本文算法的平滑效果

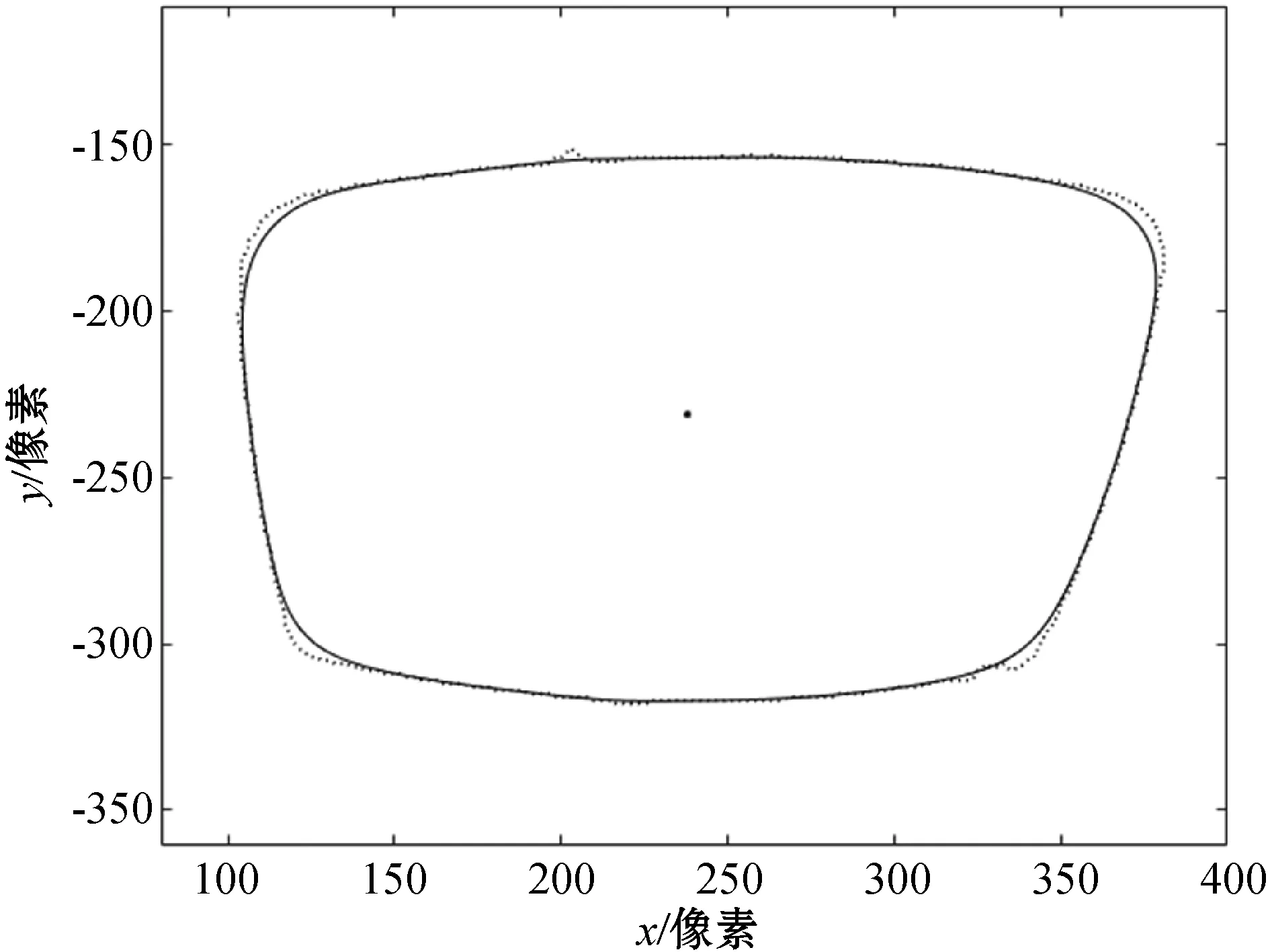
图12 滑动平均法的平滑效果

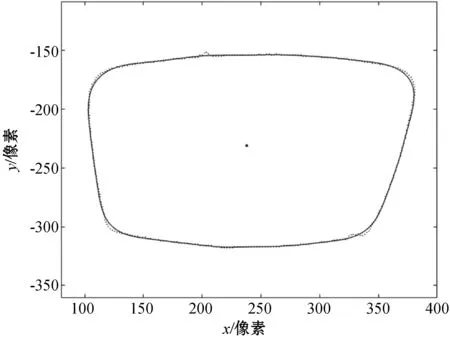
图13 Savitzky-Golay卷积平滑法的平滑效果

图11为本文方法的平滑效果,与平滑前的轮廓较吻合,且得到的是全凸的轮廓曲线,实现了保凸平滑。图12是滑动平均法平滑效果,也实现了保凸平滑,但是可以看出在曲率较大的地方平滑后的轮廓曲线与平滑前的偏差较大。图13是Savitzky-Golay卷积平滑法的平滑效果,手动设置平滑10 000次后,没有得到全凸的曲线,且在曲率较大的地方平滑后的轮廓曲线与平滑前的已经出现严重偏差,因此可以认为Savitzky-Golay卷积平滑法无法实现保凸平滑。三种平滑方法处理结果的对比如表1所示。表1中的偏差是指平滑处理后轮廓上的点列与平滑处理前的轮廓曲线的平均距离。

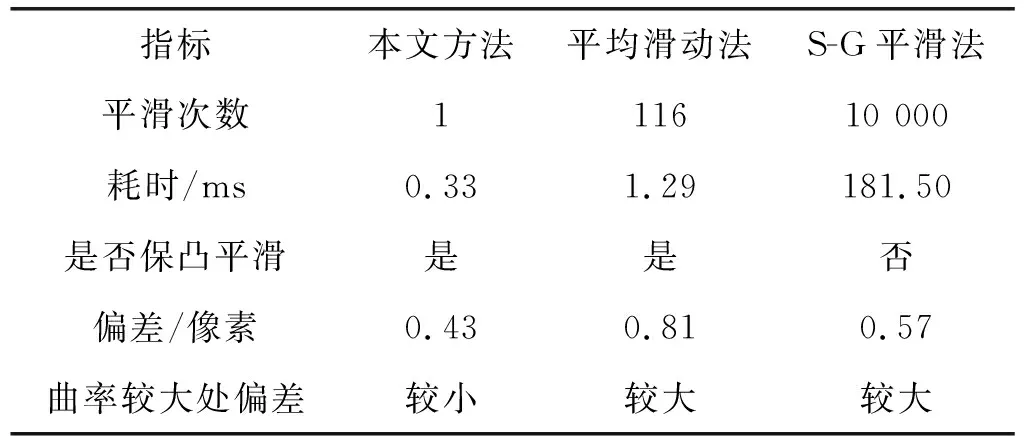
表1 三种方法平滑结果的对比

5 结 语

针对眼镜片自动磨边机系统中被用来磨削加工的眼镜片轮廓曲线数据,本文提出一种全新的平滑算法:以得到全凸的轮廓曲线作为限制条件实现了对数据的保凸平滑。通过实验对比,验证了在以得到全凸的光滑曲线为目的的条件下该算法相较于传统的滑动平均法、Savitzky-Golay卷积平滑法在耗时和平滑效果上都有显著优势。因此本文算法是一种专门适用于全凸曲线数据的保凸平滑的处理方法。