基于小波包分析的老旧拱桥损伤识别与试验
佘嘉宸 熊治华 张煜 马驰骋 朱厚达
(西北农林科技大学水利与建筑工程学院,陕西 咸阳 712100)
一、引言
据调查,我国农村地区数量众多的老旧桥涵面临着性能严重退化、病害多发的问题,尤其在我国西北地区,受历史、经济和技术等因素限制,农村老旧桥涵特别是老旧拱桥的问题更为突出[1]。基于我国大量小跨径拱桥性能退化较严重与随着我国经济发展而不断提高的交通运营需求的矛盾,对老旧拱桥开展现场检测及损伤识别具有重大的现实意义。
虽然桥梁结构损伤识别领域已经探究出许多行之有效的方法,但这些方法大多需要依靠专业设备或实验室,基于这些方法开展桥梁检测的成本是经济欠发达地区难以承受的。本文在现存研究成果的基础上,使用基于动力指数的损伤识别方法,以陕西省汉中市某桥为研究对象,在现场开展动载试验,测得桥梁选定测点的加速度时程信号,使用有限元分析模型模拟对应测点的定量损伤,得到模拟数据,利用小波包能量变化率平方和(WPERSS)处理实测与模拟数据,并运用可视化分析识别该拱桥损伤,得出定量的损伤识别结果。
二、基于小波包分析的损伤指标
小波包分析方法一般指小波包分解,这是一种对小波变换扬长避短的方法,可以对信号的低频部分和高频部分分解,如图1所示,能更好的处理包含中、高频信息的信号。[2]在桥梁结构损伤识别领域,朱劲松等[3]提出了基于小波包分解的损伤识别指标——能量变化率平方和(WPERSS),并通过对该指标的可视化分析识别桥梁结构的损伤。

图1 小波包分解示意图
在桥梁结构发生损伤的情况下,其结构响应信号的末端频率亦会随之发生波动,进而引发小波包分解的某些节点能量发生变化,又因为各个节点的能量对响应信号的波动十分敏感由此即可判断桥梁结构的损伤。本文为了有效识别桥梁结构损伤,利用了基于小波包分析方法的小波包能量变化率平方和这一指标。小波包能量变化率平方和指标(WPERSS)为:
三、荷载试验
(一)桥梁背景信息
试验桥梁位于陕西省城固县。该桥是当地重要的交通枢纽,始建于1977年,1982年竣工通车,距今40余年,桥梁总长73.7m,桥宽8m,上部结构为双曲拱、下部结构为重力式桥台,如图2所示,是一座典型的老旧拱桥。由于修建时间较远,桥梁的病害较为严重。

图2 试验桥梁
(二)有限元建模
基于实地调研获取的资料,建立桥梁的有限元模型,以开展试验前的分析。建模主要模拟主拱肋部分。其长50m、宽8m,为钢筋混凝土双曲拱结构,共有5拱肋4拱波。主拱肋厚1.2m,每道拱肋、拱波横桥向宽0.89m。拱轴线为悬链线,拱上顶点净高12.6m。主拱上左右各有5道腹拱,腹拱厚0.8m。桥面板厚0.3m。
全桥以杆系单元模拟,拱肋和桥面以全约束连接单元连接。建立有限元模型如图3所示。其中,材料选取方面,桥面系与纵向主拱肋、横向拱波、横联采用C50混凝土,腹拱横墙采用石材。
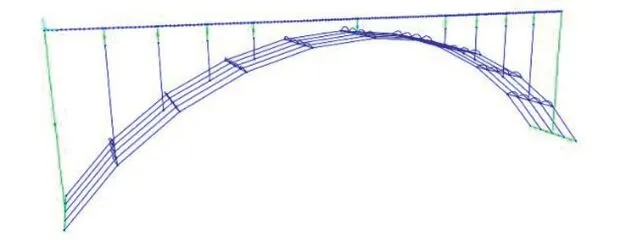
图3 三流水桥有限元模型
(三)试验概况
根据有限元模拟的计算分析结果,一共选取5个测点,从左到右分别为:左数第二腹拱中点(测点1)、第二拱腹处(测点2)、第三腹拱中点(测点3)、拱中点(测点4)、主拱偏右中点(测点5),如图4所示。

图4 加速度测点布置示意图
用全重33.6kN,前轴重15.60kN,后轴重18.20kN,前后轴距为3m的车辆分别以时速30km、40km、50km的速度行驶模拟环境激励,利用便携式加速度传感器采集汽车动载作用下、不同速度条件下各个测点的加速度时程信号,采样频率为10Hz。
四、损伤识别
选取db20小波将动载试验所测得的不同车速的加速度时程响应信号和有限元分析模拟所得的响应信号分解到第2尺度,计算WPERSS值,并作图如图5、图6、图7所示。

图5 时速30km 时,各测点WPERSS 值

图6 时速40km 时,各测点WPERSS 值
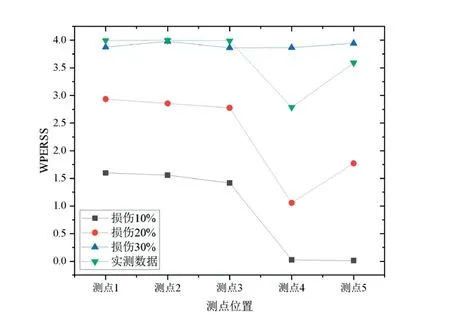
图7 时速50km 时,各测点WPERSS 值
由图可知,测点1、测点2和测点3处损伤程度相近且损伤情况较严重,约为30%;测点4和测点5损伤情况较为轻微,约为25%;测点5损伤情况介于测点1、测点2、测点3和测点4之间,约为30%。
五、结语
本文以陕西省汉中市城固县某桥为背景工程,运用数值分析模型,以荷载试验的数据为基础,利用基于小波包分析方法的损伤识别指标——能量变化率平方和(WPERSS)对其开展损伤识别,并使用可视化分析方法和BP神经网络得出损伤识别结果。该桥左数第二腹拱中点(测点1)、第二拱腹处(测点2)和第三腹拱中点(测点3)处损伤程度约为30%,拱中点(测点4)的损伤程度约为25%,主拱偏右中点(测点5)的损伤程度约为30%。
本文特别感谢陕西省汉中市城固县交通运输局对科研试验提供的帮助。

