基于非接触自适应阻抗控制的液压机械臂主/被动联合柔顺控制

王诗虎，蒋 林,，赵 慧,，朱发强，张兆威，刘焕钊

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机器人与智能系统研究院，湖北 武汉，430081)

大型液压机械臂在与环境接触时会产生较大的接触力，通常需对机械臂实施柔顺控制以保障人机物理接触安全。柔顺控制可分为主动柔顺控制和被动柔顺控制[1]，其中主动柔顺控制通过检测机械臂末端的实际位移以及机械臂与环境之间的接触力并结合阻抗控制等控制方法来调整机械臂的输入，被动柔顺控制则是通过改造机械臂结构以调节其刚度，从而使关节产生被动柔顺性。主动柔顺控制响应速度较慢，往往在机械臂与环境之间产生较大接触力后才开始调整机械臂的输入，而被动柔顺控制响应较快，在主动柔顺控制生效之前就可以实现机械臂的被动柔顺，但被动柔顺控制不能使机械臂逃离碰撞物并保持在一个安全状态，此时需结合主动柔顺控制以合理控制机械臂。柯贤锋等[2]搭建了具有被动柔顺性的液压缸单腿结构并辅以基于力反馈的位置型主动柔顺控制机制，在一定程度上提升了控制效果，但仍存在主动控制参数不能根据需要来调节、被动柔顺的刚度调节范围有限以及冲击力减幅不大等问题；Toshio等[3]将非接触阻抗控制与神经网络算法结合，利用梯度下降法将价值函数最小化以获取所需的虚拟阻抗参数，但由于末端执行器仍采用传统的阻抗控制，所以系统稳定性一般；樊绍巍等[4]将具有柔性关节的灵巧手与自适应阻抗控制结合，减小了非线性摩擦与重力对灵巧手的影响，提高了灵巧手的位置控制精度；赵新宇[5]使用遗传算法对阻抗控制参数寻优，加入了自适应控制策略，但仅对机械臂末端进行了动力学参数辨识，因此机械臂的控制精度不高；朱雅光[6]将自适应阻抗控制与模糊算法结合，利用后者对自适应控制参数进行在线修正，并将其应用于步行机器人的腿部，结果表明，仅仅修正参数无法应对较复杂的使用环境，如机器人腿部突然遭遇障碍物时可能会影响腿部受力；Chen等[7]在传统的阻抗控制中引入积分项以提高跟踪误差，同时将阻抗控制中的惯性、阻尼、刚度等的整数项改为相应的分数项，系统柔顺性能获得明显提升；金玉阳等[8]将自适应阻抗控制与模糊控制器结合，对阻抗控制参数进行自适应调节，并将其应用于飞机清洗臂，明显提高了清洗臂的位置控制精度和柔顺性；相比传统的阻抗控制，戚毅凡等[9]提出了一种基于改进型神经网络的阻抗控制方法，先利用粒子群优化算法来调整神经网络中的权值矩阵，再结合阻抗控制器即可实时调整阻抗参数以减小机械臂力控制误差和位置控制误差；王剑等[10]提出了一种基于阻抗和导纳控制的加权混合控制策略，能够大幅减小机械臂运动过程中的震荡幅度，使机械臂在不同的环境中都具有良好的柔顺性；本课题组[11]采用一种变阻尼阻抗控制，借助速度控制与PI控制相结合的阻抗控制策略，在机械臂与环境接触时实现了零稳态误差。

为了进一步提高机械臂的柔顺性，使机械臂在安全性与运动性方面都能有所保障，本文构建了四自由度液压柔顺机械臂模型，对已有的间接自适应阻抗控制方法[12]进行改进，在引入非接触阻抗控制理论的基础上，将液压柔顺机械臂与非接触自适应阻抗控制结合，利用MATLAB/Simulink仿真平台对机械臂的主、被动联合柔顺控制效果进行了分析与验证。

1 阻抗控制

1.1 间接自适应阻抗控制

基于位置的阻抗控制[13]已被广泛应用于工业机械臂的柔顺控制，但该控制机制对机械臂与环境的接触力跟踪精度不高，因此，本研究采用一种间接自适应阻抗控制方法来提高接触力的跟踪精度。

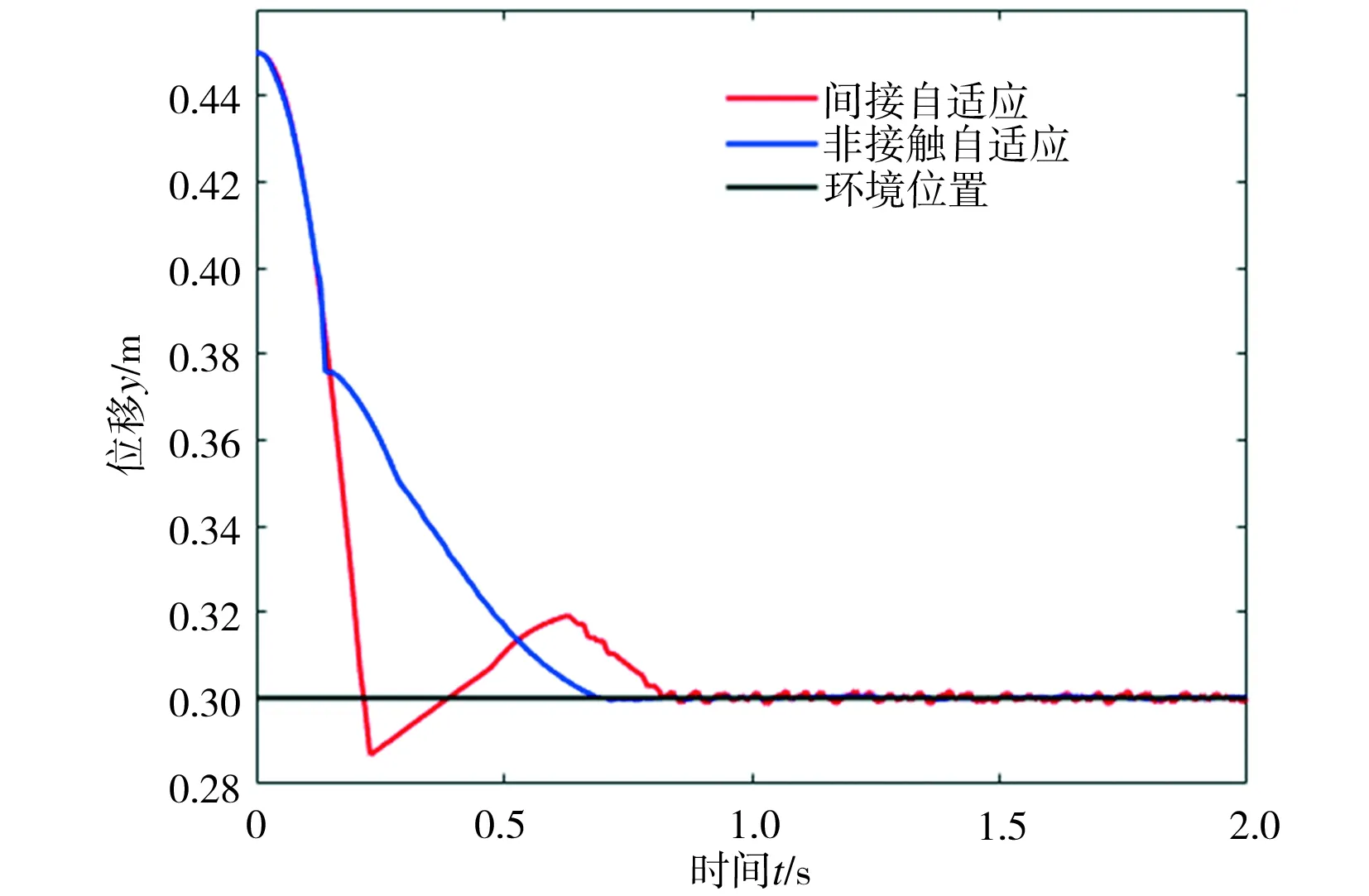
当液压机械臂末端与环境发生碰撞时，机械臂末端所受到的力Fm为

Fm=ke(xm-xe)

(1)

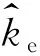
(2)

令kx=kexe，带入式(1)，则有

Fm=ke(xm-xe)=kexm-kx

(3)

(4)

(5)

(6)

液压机械臂在期望位置与实际位置之间的阻抗模型为

(7)

式中，M、B、K分别为系统的质量、阻尼及刚度，e=Fr-Fm。将式(6)代入式(7)，可得改进的阻抗模型为

(8)

(9)

式中，Γ的表达式为

(10)

(11)

则李亚普洛夫函数的导数为

(12)

(13)

(14)

再分别对式(13)和式(14)进行积分，可得环境刚度和环境位置的估计值分别为

(15)

(16)

根据所求环境刚度和环境位置的估计值，可以获得液压机械臂末端位移的调整值为

(17)

利用式(15)、(16)、(17)计算出环境刚度和环境位置的估计值并调整期望轨迹，能够有效提高期望接触力的跟踪精度。图1和图2所示分别为间接自适应阻抗控制的原理及MATLAB模型。

图1 间接自适应阻抗控制原理图

图2 间接自适应阻抗控制MATLAB模型

为了更准确地计算出环境刚度和环境位置的估计值，设定间接自适应阻抗控制参数如表1所示，其中γ1和γ2是给定的正常数，ke(0)和xe(0)是环境刚度和环境位置的初始值，均为默认常量。

表1 间接自适应阻抗控制参数

当液压机械臂与环境发生碰撞时，由间接自适应阻抗控制机制确定的期望位置xr经逆运动学求解转化为关节角度后输入普通液压关节，再经正运动学求解转化为液压机械臂末端三个方向的实际位移xm。

根据液压机械臂末端的实际位置[0.45,0,0.5]，设置x、y、z三个方向环境的位置xe、ye、ze分别为

(18)

设定期望接触力Fr为1 N，液压机械臂末端在三个方向上与环境发生碰撞后，会经过间接自适应阻抗控制生成期望位置xr。

图3所示为间接自适应阻抗控制下，借助MATLAB仿真模拟所得无被动柔顺性的普通液压机械臂末端在x、y、z方向上的位移变化。由图3可以明显看出，液压机械臂先与环境发生较剧烈的碰撞，然后在接近环境位置处趋于平稳，这种状况对液压机械臂十分不利，因为瞬时产生的冲击力可能会损害机械臂结构，为了解决这个问题，本研究引入非接触阻抗控制机制对间接自适应阻抗控制进行改进。

(a)x方向位移

1.2 非接触自适应阻抗控制

间接自适应阻抗控制只在液压机械臂末端与环境接触时才发挥作用，未与环境接触时，机械臂会按照原定输入运动，这样虽能保证机械臂的运动特性，但安全性不足，因此，本研究在间接自适应阻抗控制基础上引入非接触阻抗控制，再通过轨迹选择来调整机械臂的输入轨迹。

假设以液压机械臂末端为圆心划定一个半径为r的圆形区域，当机械臂末端实际位置xm与环境位置xe之间的差值小于r时，系统将主动减小液压机械臂末端的运动速率来实现非接触自适应阻抗控制。

令液压机械臂的输入轨迹为xr1，由间接自适应阻抗控制算法得到的机械臂末端轨迹调整值为xr2，非接触阻抗控制对机械臂输入轨迹的调整值为xr3，则液压机械臂的实际输入轨迹xc为

(19)

式中，ex为液压机械臂与环境之间的位置差。非接触阻抗控制模型表达式为

(20)

式中，M0、B0、K0分别为设定的系统虚拟质量、虚拟阻尼及虚拟刚度；Fv为虚拟力。令dxr的计算式为

dxr=xr3-xr2

(21)

当ex小于非接触范围半径r时，非接触阻抗在位置差介于间接自适应阻抗控制计算所得调整值xr2与非接触阻抗控制计算所得调整值xr3之间时发挥作用，所以非接触阻抗控制施加的虚拟力为

(22)

同时，有

Fv=Fr-Fm

(23)

联立式(20)、式(22)及式(23)可以得到非接触阻抗控制的方程为

K0(xr3-xr2)=Fr-Fm

(24)

根据式(24)即可求得非接触阻抗控制对液压机械臂输入轨迹的调整值xr3。图4所示为非接触自适应阻抗控制的MATLAB模型。

图4 非接触自适应阻抗控制MATLAB模型图

通过MATLAB仿真模拟，设定非接触阻抗控制下的r为0.1 m，系统虚拟质量M0、虚拟阻尼B0及虚拟刚度K0的无量纲值依次为0.1、1、1，将间接自适应阻抗控制与非接触自适应阻抗控制分别作用于不具有被动柔顺性的普通液压机械臂，得到不同控制机制下机械臂末端的实际位移如图5所示。由图5可见，当液压机械臂末端与环境之间的距离接近0.1 m时，非接触自适应阻抗控制下的液压机械臂末端实际位移变化曲线相比间接自适应阻抗控制下的相应曲线更平缓，这表明非接触自适应阻抗控制在保证液压机械臂运动性能的同时也能兼顾安全性。

(a)x方向

2 液压被动柔顺关节与非接触自适应阻抗控制

2.1 液压被动柔顺关节模型

构建具有被动柔顺性的4自由度液压机械臂模型如图6所示。该模型由1个液压被动柔顺回转关节和3个液压被动柔顺摆动关节组成，关节的驱动装置为液压转角自伺服阀[14]，柔顺装置为力矩传递机构[1]，该系统主要基于力矩传递机构的回退原理而使液压关节具有被动柔顺性，本研究中力矩传递机构的主要参数设定见表2，其中R为力矩传递盘的半径，k为支撑轮机构的弹簧刚度系数，γ为托盘斜坡的角度，根据这些参数可以计算出阀芯的回转角度。

图6 液压机械臂结构

表2 力矩传递机构参数表

D-H(Denavit-Hartenberg)参数法[15]是标定两个相邻连杆之间坐标系变换的方法，主要借助4个参数来描述连杆长度ai-1、连杆转角αi-1以及连杆偏距di和关节角θi等物理量，可分为标准的D-H参数法和改进的D-H参数法，前者将坐标系建立在连杆远端，而后者则将坐标系建立在连杆的近端。本研究采用改进的D-H参数法建立液压柔顺机械臂的D-H参数模型，定义回转关节的长度为0.5 m、3个摆动关节的长度均为0.15m，液压机械臂的初始位置为[0.45,0,0.5]，主要D-H参数见表3。

表3 液压机械臂的D-H参数

将非接触自适应阻抗控制用于液压被动柔顺关节，具体控制原理如图7所示。根据图7，将非接触自适应阻抗控制生成的期望位置xr经过逆运动学求解转化成角度后输入液压被动柔顺关节，再经过正运动学求解转化成机械臂在空间三个方向上的位移，结合环境位置和环境刚度计算出液压柔顺机械臂与环境的实际接触力，然后利用雅可比矩阵的虚功原理计算出液压柔顺机械臂每个关节所受的负载力矩，最后将负载力矩带入力矩传递机构，计算出液压伺服柔顺关节回退的角度，从而使关节表现出柔顺性。

图7 非接触自适应阻抗控制原理图

2.2 液压机械臂正、逆运动学

2.2.1 液压机械臂的正运动学

液压机械臂相邻关节广义坐标系的转换矩阵为

(25)

将表3所列液压柔顺机械臂的D-H参数代入上式，得到两个相邻关节之间(机械臂基座标记为0)的转换矩阵分别为

(29)

式(26)～式(29)中，Si=sinθi，Ci=cosθi，i=1，2，3，4。由此可知液压柔顺机械臂第4个转动关节到基坐标系的转换矩阵为

(30)

液压柔顺机械臂末端执行器到基坐标系的位置矢量为

(31)

式中，a4为机械臂末端执行器的长度。从而液压柔顺机械臂末端在三个方向的位移可分别表示为

(32)

2.2.2 液压机械臂的逆运动学

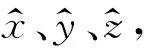
(33)

当误差f小于设定的误差阈值0.001时，停止迭代，并输出此时液压柔顺机械臂四个关节的角度θ1、θ2、θ3、θ4。

2.3 雅可比矩阵

根据表3所示液压柔顺机械臂的D-H参数，液压机械臂在关节空间内的坐标为

(34)

该坐标经转换后得到液压机械臂在笛卡尔空间内的坐标为

(35)

对式(34)进行偏微分方程求解，得到雅可比矩阵为

(36)

将式(35)代入式(36)，可得到雅可比矩阵为

(37)

式中，

J11=-(a2cosθ2+a3cosθ3+a4cosθ4)sinθ1

(38)

J12=-a2sinθ2cosθ1

(39)

J13=-a3sinθ3cosθ1

(40)

J14=-a4sinθ4cosθ1

(41)

J21=(a2cosθ2+a3cosθ3+a4cosθ4)cosθ1

(42)

J22=-a2sinθ2sinθ1

(43)

J23=-a3sinθ3sinθ1

(44)

J24=-a4sinθ4sinθ1

(45)

J31=0

(46)

J32=a2cosθ2

(47)

J33=a3cosθ3

(48)

J34=a4cosθ4

(49)

已知液压柔顺机械臂与环境之间的实际接触力Fm，基于雅可比矩阵的虚功原理可以求得液压柔顺机械臂每个关节所受到的负载力矩为

T=JTFm

(50)

2.4 主、被动柔顺控制仿真与结果分析

利用MATLAB/simulink平台，对非接触自适应阻抗控制用于普通液压机械臂(即主动控制)或液压被动柔顺关节(即主被动联合控制)的状况分别进行仿真模拟[16]。仿真模拟采用四阶龙格库塔算法，设定仿真总时长为2 s，采样时间间隔为0.01 s，非接触自适应阻抗控制输入幅值为1、频率为1 rad/s的正弦波形，液压机械臂末端的初始位置为[0.45,0,0.5]，x、y、z方向上的环境位置依次为0.3、0.3、0.6，非接触阻抗控制范围半径r分别设定为0.04、0.07、0.10、0.13 m；当液压机械臂末端未与环境接触时，设定输入为正弦波形，当液压机械臂末端与环境之间的位置差ex小于设定的非接触阻抗控制范围半径r时，利用非接触阻抗控制来调整液压机械臂末端的运动速率，当液压机械臂末端与环境接触时(Fm>0)，切换到间接自适应阻抗控制来调整输入。

当r依次为0.13、0.10、0.07、0.04 m时，不同控制机制下的机械臂末端实际位移以及机械臂与环境之间接触力的仿真结果分别如图8和图9所示。综合分析图8和图9可知，随着非接触自适应阻抗控制范围半径r的变化，液压机械臂末端与环境之间的接触效果存在明显差别，主动控制都存在一定程度的延迟，相比主动控制的状况，

(a)x方向实际位移( r=0.13 m)

主、被动联合控制下机械臂与环境间的接触力变化不大，但机械臂末端位移更加平缓，机械臂的响应速度更快，表明主、被动联合控制效果更好，其中当r为0.10 m时，主被动联合控制下的机械臂运动效果最佳。

柔顺度是反映关节柔顺性的重要指标，其计算公式为

(51)

式中，Δθ为液压关节输入与输出的角度差，T为液压关节所受到的负载力矩。柔顺度越大，意味着关节在力矩的作用下产生的角位移偏差越大，关节柔顺性就越好。设定r为0.10 m，获得液压机械臂四个关节的柔顺度变化仿真模拟结果如图10所示。由图10可知，相比单一的主动控制，非接触自适应阻抗控制与液压柔顺机械臂结合后的关节柔顺度更大，柔顺性更好。

(a)x方向接触力( r=0.13 m)

(a)第一个关节(回转关节)

3 结语

本文通过引入非接触阻抗控制理论对间接自适应阻抗控制进行改进，获得非接触自适应阻抗控制，并基于液压柔顺回转关节和液压柔顺摆动关节构建了具有被动柔顺性的四自由度液压柔顺机械臂模型。利用MATLAB/simulink仿真平台，将非接触自适应阻抗控制作为液压机械臂的主动柔顺控制并与关节的被动柔顺控制相结合，实现对关节的主、被动联合柔顺控制。仿真结果表明，在非接触自适应阻抗控制与被动柔顺控制共同作用下，液压机械臂的柔顺度更高，柔顺性更好。