Arrhenius 公式和环境作用动力学对压缩橡胶的精度比较
封先河,魏小琴,杨万均,何建新,李迪凡
(西南技术工程研究所,重庆 400039)
橡胶制成的O 形密封圈常作为密封材料,广泛应用于油、气、水等管道的密封和武器装备。特别是火箭发动机的密封,长期工作或者仓库贮存时,由于受机械应力、介质及空气中氧和温度的作用,O 形密封圈产生累积永久变形,导致其压缩比减小而引起泄漏,丧失密封性能,进而导致整个密封系统的功能丧失或报废,故需对其老化寿命进行预测[1-13]。准确预测其老化寿命的前提是对O 形密封圈老化规律的精准描述。
现行的老化寿命评估方法基本上是采用阿伦尼乌兹公式及其修正公式,并且建立了一系列标准[14-16]。比如GJΒ 92.1 和GJΒ 92.2,以及GΒ/T 27800—2011《静密封橡胶制品使用寿命的快速预测方法》、GΒ/T 3512—2014《硫化橡胶或热塑性橡胶热空气加速老化和耐热试验》。在对这些标准和阿伦尼乌兹公式的实际使用过程中,有时会存在着较大的预估误差。
环境作用动力学作为一种新的理论[17-21],正在逐步得到广泛的应用。本文通过氟硅橡胶高温加速试验获取的试验数据,分别采用环境作用动力学通解和阿伦尼乌兹公式建立了氟硅橡胶压缩永久变形率模型,通过3.5 a 的自然环境试验数据与其进行对比研究。
1 原理
1.1 阿伦尼乌兹公式
早在19 世纪,人们就已经知道温度对反应速率影响的定性规律。荷兰化学家Van't Hoff 指出,在室温附近,温度升高10 ℃,反应速率增至原来的2~4倍。这条经验规律称为Van't Hoff 规则。
1889 年,瑞典化学家Arrhenius(阿仑尼乌斯)在研究蔗糖水解速率与温度关系时,提出了如下经验公式:
式中:R为热力学常数;k为反应速率;A为指前因子或频率因子;Ea为Arrhenius 活化能。A和Ea是Arrhenius 方程中2 个重要参数。
1.2 环境作用动力学
环境作用动力学建立于21 世纪初,是一个新兴的理论。经过10 多年的发展,理论更加成熟,应用逐渐增多,涉及弹簧、橡胶、塑料、弹链、胶粘剂、吸波结构等材料及零部件。环境作用动力学由活化粒子、活化粒子浓度、变化进程、变化度量值、环境作用、特征能量值、环境适应性、环境响应性、变化重复性等8 个主要定义和2 个主要假设组成[20],由假设2 构建了环境作用动力学方程:
式中:I(t,T)为变化度量值;j为比例系数,同时平衡量纲;S(t)为环境适应性;U(T)为环境响应性;Q(t,T)为变化重复性;σ为环境作用。
2 氟硅橡胶压缩永久变形模型建立
2.1 压缩永久变形温度加速试验
试验条件基本情况如下:
1)试验对象:火箭发动机的氟硅橡胶O 形圈。
2)试样状态:试样无孔隙、裂纹、杂质、气泡、毛边和机械损伤,表面应当光滑、清洁。试样处于受压状态,在特制夹具中进行,压缩率为23%。
3)试验温度:选取了100、125、150、175、200 ℃等5 个温度点作为热空气加速老化温度,每个温度点以3 个试件做平行试验。
4)试验设备:热老化设备为CS101 型电热鼓风干燥箱。
5)性能指标:压缩永久变形率ε。
6)试验标准:参照GΒ/T 7759—1996《硫化橡胶、热塑性橡胶 常温、高温和低温下压缩永久变形测定》检测压缩永久变形率;参照HG/T 3087—2001《静密封橡胶零件贮存期快速测定方法》计算氟硅橡胶O 形圈的贮存老化寿命。
首先校正老化烘箱及温度计,测量橡胶圈的原始高度h0,并将O 形橡胶圈按确定的压缩比(23%)安放在夹具内,投入高温老化箱内,按一定周期取出,在标准温、湿度环境下恢复2 h,测量老化后高度h2,按照式(2)计算压缩永久变形率ε:
式中:h1为夹具限制器高度;h2为老化后高度;h0为橡胶圈的原始高度。试验结果见表1。
2.2 基于阿伦尼乌兹公式的氟硅橡胶压缩永久变形模型
按照阿伦尼乌兹公式(1),于是有:
两边同时除以h0,有:
其中:h1/h0=0.758。应用氟硅橡胶压缩永久变形温度加速试验数据,有:A=0.972 45,K25=0.000 214,α=0.74。于是得到25 ℃基于阿伦尼乌兹公式的氟硅橡胶压缩永久变形模型为:
2.3 基于环境作用动力学的氟硅橡胶压缩永久变形模型
氟硅橡胶O 形圈的变化度量值I定义为:I=h2/h0。其中,h1为夹具限制器高度;h2为老化后高度;h0为橡胶圈的原始高度。
压缩作用为压缩变形量h1/h0减去老化度量值I,随着自由长度的变化,压缩作用σ也是变化的。即:
应用环境作用动力学方程可以得到压缩橡胶的永久变形[22]为:
应用氟硅橡胶压缩永久变形温度加速试验数据,构建误差函数Y:
式中:Ii为加速试验数据,Ii(ti,Ti)为计算数据;n为加速试验数据个数;i=1-n。采用全局最优化计算方法,使得函数Y最小,于是有:E0=-15 172,f=-0.136,g=97.046。
代入式(10)得基于环境作用动力学的氟硅橡胶压缩永久变形模型:
3 阿伦尼乌兹公式模型和环境作用动力学模型对比研究
3.1 自然环境试验
氟硅橡胶压缩永久变形试验采用温度加速试验相同的样品、工装、测试方法,试验地点在海南万宁试验站库房,年平均温度为27.6 ℃。
3.2 阿伦尼乌兹公式模型和环境作用动力学模型对比
将阿伦尼乌兹公式模型、环境作用动力学模型和试验结果进行对比(以海南万宁试验站库房年平均温度为准),如图1 所示。图1 中,圆点表示海南万宁试验站库房实际的试验数据,环境作用动力学的模型靠近实际的试验数据,阿伦尼乌兹公式模型偏差较大。数值误差比较见表2。
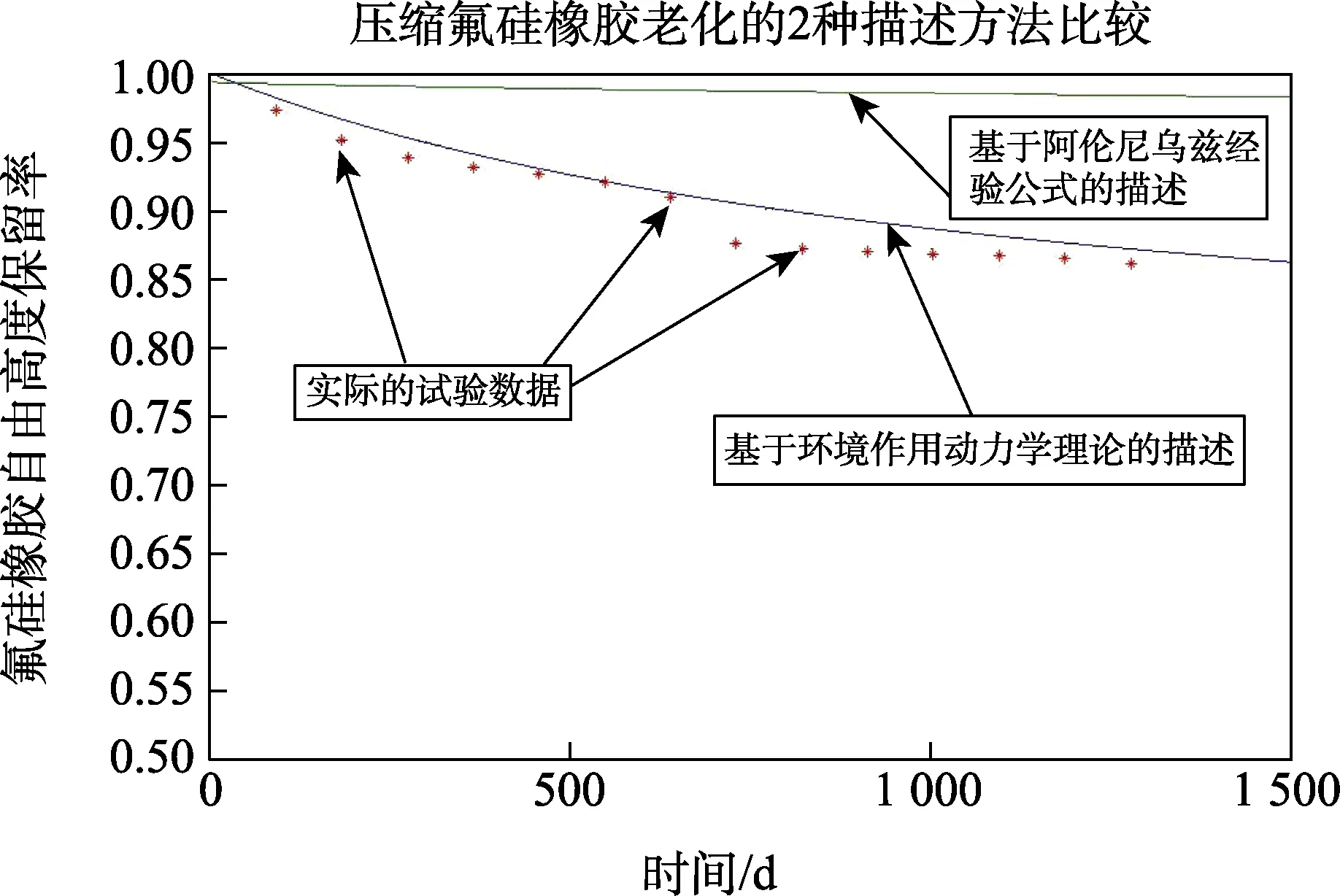
图1 阿伦尼乌兹公式模型和环境作用动力学模型对比 Fig.1 Comparison between Arrhenius formula model and environmental action dynamics model

表2 误差比较 Tab.2 Error comparison
3.3 结果分析
阿伦尼乌兹公式由于不能引入环境作用的概念,将压缩量固定为夹具限制器高度h1,与实际情况不符,因而造成较大误差。同时,固定的活化能也是阿伦尼乌兹公式一个误差来源。
压缩氟硅橡胶在开始时(时间t=0),氟硅橡胶的原始长度为h0,受到的压缩量是h0-h1。经过一段时间后,在t=t1时刻氟硅橡胶的长度变为h2,受到的压缩量是h2-h1。直到t=∞,氟硅橡胶的长度变为h1,受到的压缩量是为0。
环境作用动力学模型,以压缩作用σ考虑了压缩氟硅橡胶压缩量的变化,从而更加准确地描述了压缩氟硅橡胶的变化规律。同时,用E0+fT2+gT表示的活化能更加精准。
4 结论
由于阿伦尼乌兹公式没有考虑环境作用的影响,或者说只考虑了固定环境作用的影响,因此阿伦尼乌兹公式只适用于没有环境作用或固定环境作用下的物质特征变化。环境作用动力学方程中,有明确的环境作用项σ,适用于复杂环境作用下的物质特征变化规律描述。压缩氟硅橡胶存在变化的压缩作用σ,应用环境作用动力学更加合理。实际结果证明,阿伦尼乌兹公式模型与自然环境试验数据最大误差为14.25%,环境作用动力学模型与自然环境试验数据最大误差为3.32%。

