基于海洋浮标的电场干扰特性分析及信号检测方法

孙强, 张伽伟, 喻鹏

(1. 海军工程大学 兵器工程学院，湖北 武汉430033; 2. 海军士官学校 兵器系，安徽 蚌埠233000)

0 引言

近年来，UUV、AUV、各类水中浮标、滑翔机等新兴水下平台因体积小、数量多、造价低等诸多优势而得到飞速发展[1-2]。其中，水中探测浮标相比于其他水中平台具有以下3 点优势：布放灵活，适合大面积布放或临时机动布放；平台稳定，环境适应性强，浮标可调节悬浮于水中任意深度平面，且平台相对稳定，利于各类探测传感器的目标探测；自持力久，由于浮标不需要动力等其他辅助载荷，除工作系统外可携带更多的电池，可根据需要工作更长时间。基于上述3 点优势，探测浮标被广泛用于民事和军事用途，比较有代表性的是当前构建的以Argo 浮标为基础全球实时海洋观测网[3]，已经覆盖全球各大洋，美军的磁探测浮标可对浮标周围800~2 000 m 范围内的水中目标进行有效探测。

探测浮标技术和电场探测技术的发展为水中目标的探测提供了新的途径。将电场探测与浮标探测相结合能获得更好的目标探测效果，可充分发挥电场探测和浮标探测的优势。

国内目前还没有加装电场探测系统的浮标，对浮标平台的电场干扰特性和信号检测方法缺乏研究，而针对目标电场信号检测提出了较多的检测方法，如线谱检测、匹配滤波、小波分解、能量检测和自适应门限检测等[4-13]，与浮标平台相结合的检测方法研究较少[14]。

为解决基于浮标平台的电场测量和信号检测的问题，本文在海上试验的基础上，详细分析了电场探测浮标不同阶段、不同水深的干扰来源及其特性，明确了电场探测浮标的特点，并结合目标电场的信号特征，提出了自适应门限的线谱能量加和检测方法，实验结果表明，该方法在保证不降低探测概率的情况下，可有效降低探测虚警率，适用于电场浮标探测。

1 电场探测浮标干扰特性分析

排除浮标自身的电场干扰外，理论上，电场探测浮标的干扰主要来自两个方面：一是风浪等自然因素引起海水扰动，而切割地磁场产生的感应电场，其大小与风浪大小、测量点水深因素有关，通常情况下风浪越大、测量点越接近水面干扰电场越大，随着水深的增加而减小，最高可达数十μV/m的量级；另一方面是电场传感器及导线运动切割地磁场而产生的干扰电场(通常被称为晃动干扰)。

为了充分分析电场探测浮标干扰特性2019 年9 月在南海某海域开展了实测试验，测量海域水深2 500 m，浪高1.5 m，距离陆地200 海里。电场测量系统采样率为1 000 Hz，探测浮标示意图如图1所示，浮标工作过程为：布放后下潜至50 m 水深悬浮1 h 后，再下潜至2 002 m 后上浮，下潜至悬浮过程中浮标调节浮力的电磁阀处于工作状态。

布放入水后0~50 m 刚开始下潜过程中的电场三分量及姿态变化如图2、图3 所示，其中图2(a)~ 图2(c)为电场三分量经0.5~30 Hz 低通滤波后的时域波形。由图2(a)~图2(c)可知下潜过程中电场干扰噪声的峰峰值Ex为71.1 μV/m、Ey为1.3 μV/m、Ez为2.5 μV/m，从Ex分量可知存在较明显的干扰“毛刺”，除“毛刺”外其量级也是在 1~ 3 μV/m。图2(d)为电场三分量未经滤波在DC~ 30 Hz 内的频谱，由干扰电场频谱图2(d)可知，其干扰能量主要集中在0.5 Hz 以下，Ez分量还存在线谱干扰。需要说明的是，为降低低频干扰，采取通带为0.5~30 Hz 的2 阶巴特沃尔斯数字滤波器，其在 0.3 Hz 处衰减约为10 dB，0.2 Hz 处衰减约为 20 dB，但滤波后0.5 Hz 以下的干扰能量还是大于0.5 Hz 以上频段，干扰峰值仍然集中在0.5 Hz 以下。由图3 可知，在下潜过程中浮标存在较大的晃动角度，各方位角的波动值分别为俯仰角18.3°、横滚角16.4°、方位角23.5°，而从晃动角度的频谱可知其能量也主要集中在0.5 Hz 以下，在0.15 Hz、0.39 Hz 附近存在尖峰。

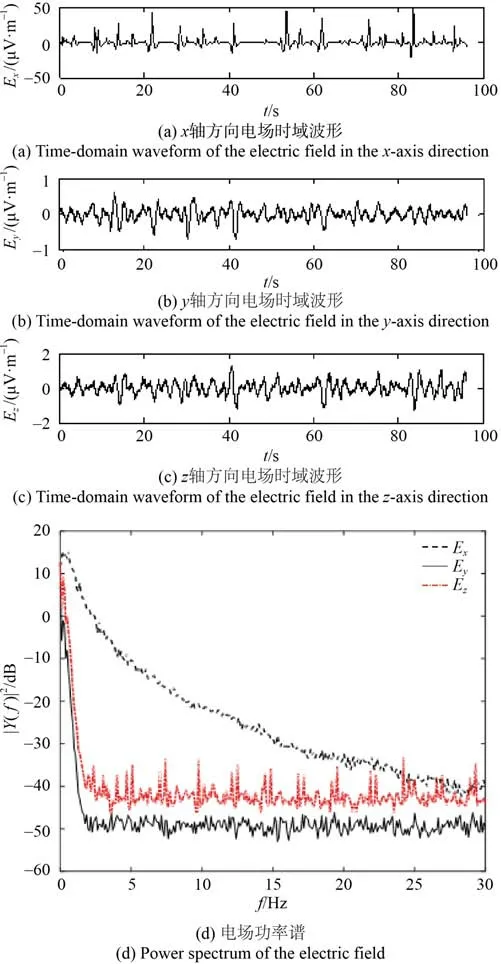
图2 下潜过程中电场三分量及频谱Fig. 2 Three components and spectrum of the electric field in the diving process

布放入水后50 m 处悬停过程中截取的部分数据电场三分量(0.5~30 Hz 带通滤波)及姿态变化如 图4、图5 所示。由图4 可知，悬浮过程中电场干扰噪声的峰峰值Ex为 36.3 μV/m 、Ey为 1.5 μV/m、Ez为1.2 μV/m。由图5 可知，在悬停过程中浮标存在较大的晃动角度，各方位角的波动值分别为：俯仰角16.0°、横滚角22.1°、方位角20.2°，晃动谱可得到与下潜过程中相同的结论。

由悬浮再到下潜过程中的电场三分量(0.5~30 Hz带通滤波)及姿态变化如图6、图7 所示，图中浮标在2 500 s左右开始匀速下潜。由图6和图7可知，再次匀速下潜时干扰电场和晃动角度都明显减小，电场峰峰值Ex降到0.2 μV/m、Ey为0.3 μV/m、Ez为 0.6 μV/m，Ex分量的“毛刺”干扰也消失，Ez分量的线谱干扰也消失，晃动角度也降到俯仰角0.9°、横滚角1.8°、方位角10.4°。

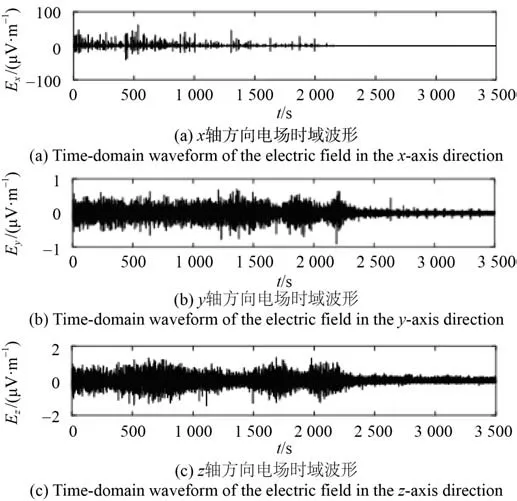
图6 由悬浮到下潜过程中的电场Fig. 6 Electric field from floating to diving

图7 由悬浮到下潜过程中浮标姿态变化Fig.7 Buoy attitude from suspension to dive

实测数据进一步分析表明：200 m 以下水深的电场干扰三轴分量峰峰值在0.1 μV/m 附近，浮标晃动角度也在0.3°左右。

通过电场探测浮标海上试验数据分析可得到以下4 点结论：

1)探测浮标在0~50 m 水深较浅深度，干扰电场较大，在μV/m 的量级，浮标晃动角度也较大，对比图2 和图3，图4 和图5，可知晃动峰值频率与干扰电场的频率是一致的(集中在0.5 Hz 以下)，说明电场干扰主要源于晃动干扰和海浪感应电磁场干扰。

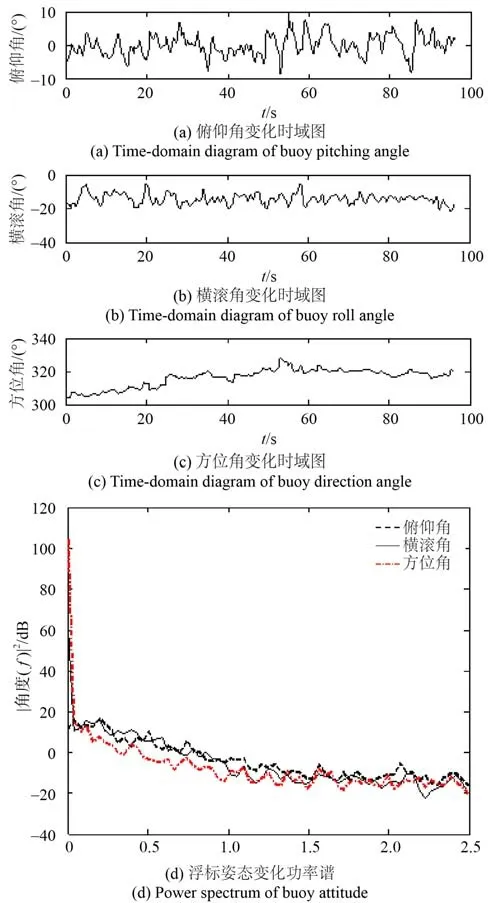
图3 下潜过程中浮标姿态变化Fig. 3 Buoy attitude in the diving process

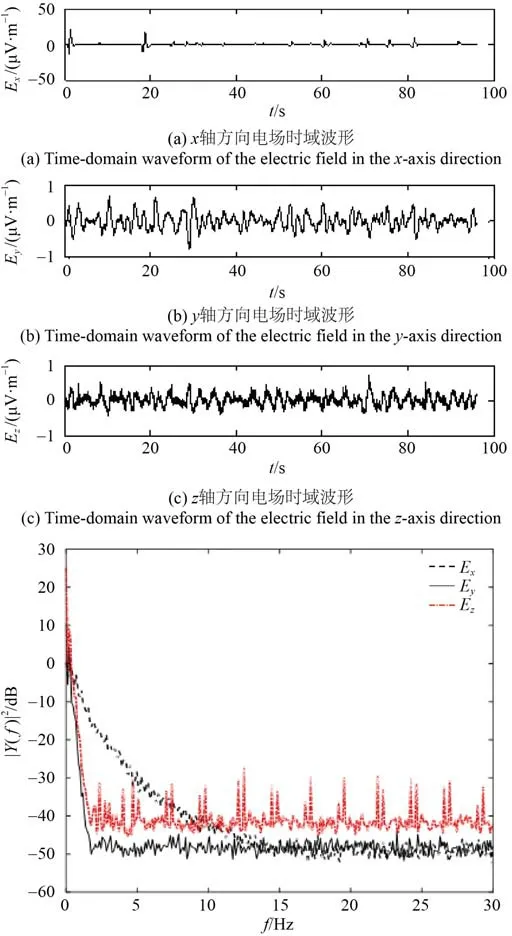
图4 悬浮过程中电场三分量及频谱Fig. 4 Three components and spectrum of the electric field during floating

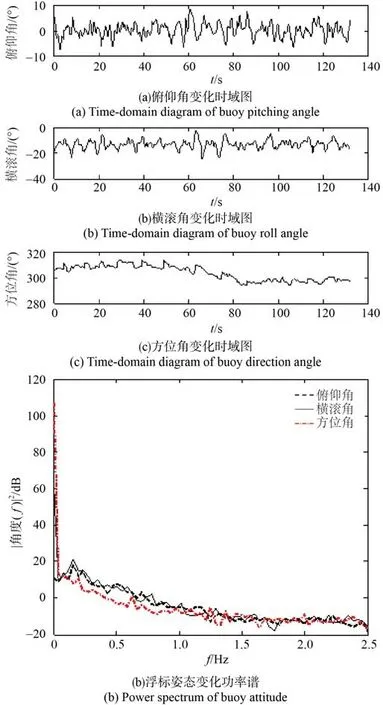
图5 悬浮过程中浮标姿态变化Fig. 5 Buoy attitude during floating

2)浮标电磁阀工作会对电场产生脉冲干扰，Ez分量还存在线谱干扰(主要原因是由于z轴分量两个传感器分别位于浮标浮力调节装置的两端，受干扰较大，而水平分量则在浮标的底部、干扰相对较小)。

3)浮标在50 m 水深悬浮时，其晃动干扰与0~50 m 下潜过程中相当，当稳定一段时间后继续下潜，晃动和电场干扰明显减小。

4)随着深度增加，干扰电场逐渐减小，干扰电场峰峰值可低至0.1 μV/m 的量级，俯仰和横滚角的变化在0.1°量级。

2 电场探测浮标信号检测算法

由第1 节分析可知，浮标由于自身晃动的原因，难以对舰船静电场信号进行探测(静电场信号频率一般在DC~0.5 Hz，极易受到晃动和海浪干扰)，而起源于轴系转动调制轴电流产生的轴频电场[15-16]，其频率主要集中在0.5 ~30 Hz，且在频域呈明显的线谱特征[17-19]，因此在浮标平台较为有效的方法是对舰船的轴频电场进行检测。然而电场探测浮标对轴频电场信号检测存在以下2 个难点： 1)不同船舶之间轴频电场信号的量级差别较大，且受浮标与船舶之间的距离影响较大，因此在采用传统的能量检测法对轴频电场信号检测时，难以确定信号的检测门限；2)试验中所用的浮标平台由于晃动和浮力调节装置的工作会存在较大的干扰，易造成检测算法的虚警。为解决上述问题1，通常采用基于自适应门限的线谱能量检测方法，信号检测流程如图8[20]所示。

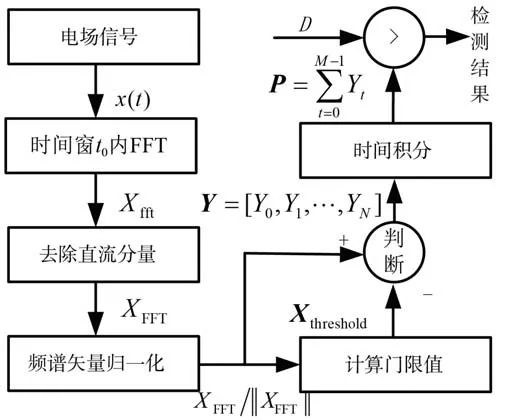
图8 线谱能量检测流程Fig. 8 Line spectrum energy detection process

信号的检测步骤具体如下：

步骤1对时间窗t0内电场信号x(t)进行FFT计算，得到其信号的频谱Xfft并去除直流分量，得到结果为XFFT。

步骤2对XFFT进行能量归 一 化(排除不同舰船源强度大小和距离对检测的影响)。

步骤3根据归一化能量，计算每个频点的检测门限值Xthreshold，门限值为自适应浮动门限与固定门限相结合其值为

式中：Median(·)表示中值滤波运算符；Δ为固定门限向量。由于检测过程中XFFT是实时变化的，从而Xthreshold是变化的，即Xthreshold为自适应门限。

步骤4比较归一化能量XFnFoTrm与门限Xthreshold的大小，疑似线谱判断向量

式中：凡是Xt＞Xthreshold,t的Yt=1则表明对应的频率Ft上存在疑似线谱，其他则Yt=0表示不 存在。

步骤5随着时间窗t0的向前滑动，会得到各时刻的疑似线谱Yt，假设以M为积分宽度，则M宽度内的积分结果可表示为

步骤 6判断Pt是否大于某一设定值D(1≤D≤M，且D为整数)，大于则判断对应的频点检测到疑似目标。

仿真和试验验证表明本文算法可有效解决浮动门限的问题，其优点是能准确得到出现疑似线谱的频率，但是存在较高的虚警，其无法甄别浮标电场测量中如图2(d)的线谱干扰。为解决虚警的问题，本文提出图9 所示自适应门限的线谱能量加和检测方法。

图9 自适应门限的线谱能量加和检测流程Fig. 9 Self-adaptive threshold line spectrum energy detection process

新的算法在“计算特征值”和“计算门限值”时做了较大的改变：

首先，“疑似线谱提取”，采用基于自适应门限的线谱能量检测相同的做法(步骤 2~ 步骤4)。

然后，“计算特征值”特征值Pt为频带内的疑似线谱点谱值之和。

而后，“计算门限值”，计算门限不再需要进行中值滤波，而是通过以下公式获得：

式中：m为门限因子为设定的常数；Pave表示当前时刻前w个时间窗内特征值的均值。由于检测过程中Pt是实时变化的，从而Xthreshold是变化的，即Xthreshold仍为自适应门限。与图8 算法不同的是，新的算法只能得到检测到目标的时刻，不能给出检测到的具体线谱频率。

3 仿真与实测数据分析

为分析对比检测算法改进前后的性能，首先进行仿真分析，通过大量实测试验数据分析表明，水面船舶轴频电场信号源强度在几十至 数百A·m[13]。为研究一般信号强度下的检测性能，仿真中假设水平时谐电偶极子模拟源强度为50 A·m，信号频率为1 Hz，并存在2 Hz、3 Hz 的倍频信号，叠加峰值为20 μV/m 的高斯噪声，电偶极子方向为x轴方向，考虑正横距离为0 m时，距离200 m 处信号峰值约为0.54 μV/m，利用本文改进算法与图8 所示的线谱能量检测算法对电场纵向分量检测，仿真次数1 000 次，得到ROC(receiver operating characteristic curve)曲线如图10 所示，由图10 可知，本文改进后的算法较原算法性能有明显提升。

图10 仿真数据ROC 曲线对比Fig. 10 Comparison of ROC curves of simulation data

进一步利用浮标平台在水面实测的42 组不同目标通过的电场数据，分析得到算法改进前后的ROC 曲线如图11 所示。需要说明的是：实测数据基本上为不同的水面船舶，且不同船舶正横距离有所差异，不同船舶的信号大小也有差异。由图11可知，在200 m 距离上，本文改进后的算法较原算法性能明显提升。

图11 实测数据ROC 曲线对比Fig. 11 Comparison of ROC curves of measured data

选取图12 所示两个不同的实船电场x轴分量进行单独分析，其中图12(a)为某货船的测量结果，图12(b)为货船通过时400~500 s 时间窗内的频谱，图12(c)为1 千吨左右的小型运油船，图12(d)为300~400 s 内的频谱。由图12 可知，货船、运油船低频电场通过特性差异明显，货船的电场还存在较大的干扰，大约在426 s 附近通过探测平台，运油船约在361 s 附近通过探测平台。

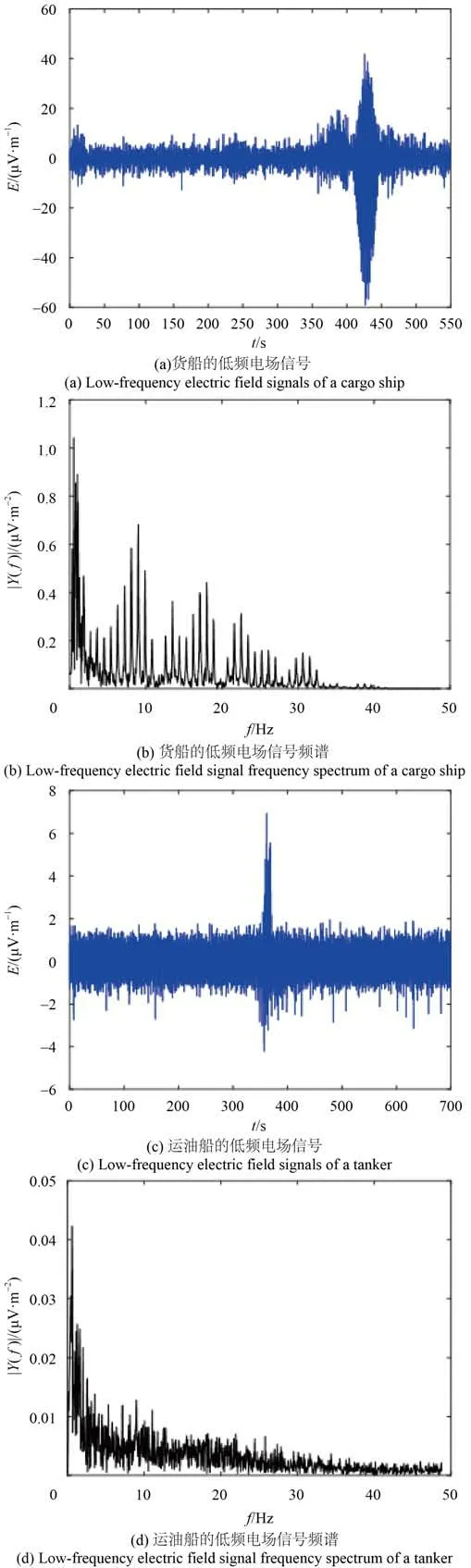
图12 两艘船舶实测低频电场Fig. 12 Measured low-frequency electric fields of two real ships

前述两种检测算法的检测结果如图13 所示。由图13(a)可知对于货船原检测算法在395 s 附近检测到了清晰的线谱倍频信号，但在其他时刻出现了较多的扰动信号，由图13(b)改进算法在371 s 附近检测到了的低频电场信号，且不存在扰 动误判；由图14(a)可知：对于运油船原检测算法存在较多扰动，基本无法准确判断何时检测到运油船的电场信号及其频率，由图14(b)改进算法在380 s 附近检测到了运油船的低频电场信号，且不存在扰动误判。

图13 货船电场检测结果Fig. 13 Electric field detection results of a cargo ship

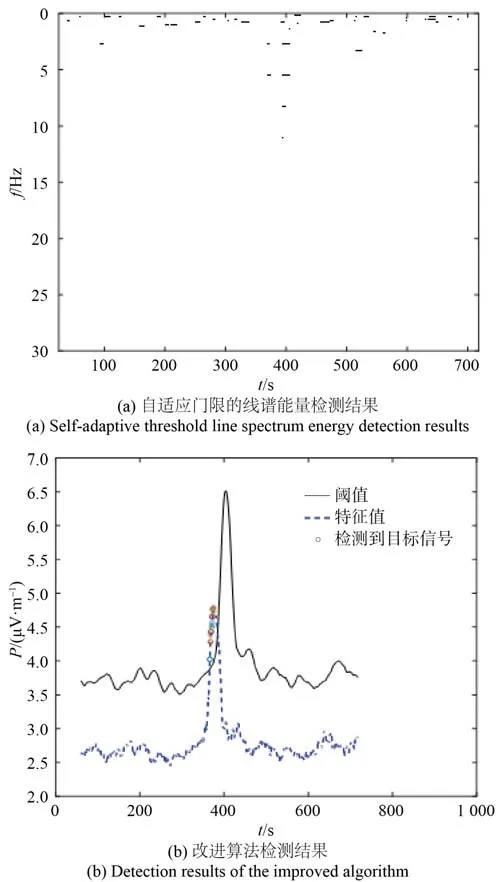
图14 运油船电场检测结果Fig. 14 Electric field detection results of a tanker

上述结果表明，自适应门限的线谱能量虽然检测距离大于本文的改进检测算法，但从抗干扰的角度后者更适合舰船电场探测浮标。

4 结论

本文通过电场探测浮标在深远海的试验研究，明确了浮标平台电磁阀工作会对安装在其附近的电场传感器产生干扰，浮标在近海水表面易受到海浪和浮标晃动的干扰，该部分干扰峰值集中在0.5 Hz以下，随着浮标工作深度的加深晃动及电场干扰逐渐减小，在200 m 水深附近浮标晃动角度在0.3°以内，电场干扰峰峰值量级为0.1 μV/m。进一步对电场探测浮标信号检测算法的研究表明，自适应门限的线谱能量加和检测方法探测概率高、虚警率低，适合应用于浮标探测平台。