考虑平台特性的多层建筑物内履带式无人平台运动规划

熊光明, 于全富, 胡秀中, 周子杰, 许佳慧

(北京理工大学 机械与车辆学院，北京 100081)

0 引言

在美国国防高级计划研究局(DARPA)的SUBT挑战赛[1]和我国的跨越险阻2021 地面无人系统挑战赛[2]中，都首次要求无人平台在多层建筑物内完成自主任务。不同于一般单层环境，多层建筑具有多个相互连接的离散平面的空间特征。虽然许多应用于单层连续平面环境的二维和三维运动规划算法已经被提出，但是无人平台在多个离散平面之间的运动规划问题仍有待解决。

运动规划算法一般分为2D、2.5D 和3D 共 3 种类型。2D 算法是在平面地图上进行规划的传统方法。2.5D 算法在2D 算法的基础上将3D 地图映射到2D 平面上并进行规划，考虑到更多环境信息的同时保证了算法的计算效率。Carsten 等[3]将3D 环境投影到平面进行栅格化，在每一个栅格上存储一个地形对应的高度值，在全局规划算法中融合障碍物的高度信息进行路径规划。Ishigami 等[4]将路径长度、俯仰和侧倾程度等4 项指标加权和作为Dijkstra 算法生成多条候选路径，但是没有考虑运动学约束。Lacroix 等[5]利用A*算法在搜索路径时，采用圆弧路径连接节点，得到相对平滑的路径，但是无法保证路径的曲率连续。Howard 等[6]利用运动学模型前向仿真生成基元路径来进一步提高路径的连续性。在单层连续平面环境下，2D 和2.5D 规划算法可以减少计算的复杂度，并同时保证规划结果具有一定的准确性。然而，2D 和2.5D规划算法并不能直接应用在多层建筑物环境中。

相对于2D 和2.5D 算法，3D 规划算法可以在单层连续曲面上进行规划，但是由于实际三维环境的空间复杂性，难以应用在多层建筑物等大规模场景。Colas 等[7]和Menna 等[8]将室内环境使用三维栅格地图建模，考虑到距离、坡度、凸起度作为代价值，最终在仿真环境下得到了楼梯处的一段可通行路径。但是仿真环境只是一段楼梯区域，没有包括各楼层环境信息，空间复杂度比较小。由于3D规划算法的复杂度大于nlog(n)，n为算法处理的节点数量，随着地图空间的增大，节点数量的增多会引起路径搜索时间的非线性激增[9]。此外，三维规划常用的地图表示方式主要为多边形网格化曲面和三维栅格地图。多边形网格化曲面要经过复杂的拟合重构步骤，难以用于大规模地图，而三维栅格地图需要对大量的稠密点云信息进行二次重构才能用于规划。加之，3D 规划算法本身的复杂度以及需要在整个路径长度上进行三维碰撞检测。因此，3D 规划算法在多层建筑物环境中需要占用大量的计算资源，难以实际应用。

除此之外，对多层建筑物内运动规划问题进行降维处理的方案也被提出。Zhang 等[10]和Baltashov 等[11]将多层建筑内3D 环境表示为多个2D 环境的组合来实现多楼层间的自主导航任务。但是，他们一方面没有考虑到环境高度信息，另一方面全局规划算法没有考虑平台特性，局部规划算法无法很好地适应多层建筑物环境空间狭小等特点，容易陷入局部最小。

针对上述情况，考虑到多层建筑物环境空间狭小特点，本文利用地图的分层表示方法将多层建筑内3D 运动规划问题降解为2.5D，利用维诺路径作为A*算法代价项，引入运动基元来实现路径的运动学可行。通过履带平台运动学模型在动力学窗口内对其轨迹进行预测，引入波阵值评估方法，避免陷入局部最小。利用有限状态机建立起无人平台模式之间的关联关系，实现多楼层建筑物内的自主导航任务。

1 多层建筑物内运动规划框架

考虑到无人平台在多楼层建筑物内进行自主导航任务时需要完成上、下楼梯等操作，本文在履带式差速底盘的基础上进行研究工作。

根据多楼层建筑物内环境的特点可以将自主导航任务分为3 种类型，同楼层内的运动规划、上楼与下楼的运动规划。针对于不同工况的特点，本文为无人平台设计了3 种不同的工作模式，并利用有限状态机决策模型(见图1)实现多楼层间的运动规划。多楼层间的运动规划算法首先进入同楼层规划模式，导航平台到达同层目标点。若满足条件1，即当前楼层小于目标楼层，则切换到上楼规划模式。若满足条件2，即当前楼层大于目标楼层，则切换到下楼模式。若满足条件3，即当前楼层等于目标楼层，则再次进入同层规划模式，最终到达目标点。

图1 有限状态机决策模型示意图Fig. 1 Schematic diagram of Finite State Machine decision model

同楼层运动规划算法如图2 所示，由全局与局部规划组成。全局规划在全局地图、维诺路径、运动基元和定位信息的基础上得到一条平滑、无碰撞的全局路径发送到局部规划。局部规划结合全局路径、局部地图、波阵值、平台运动学模型和定位信息得到最优局部路径和控制量，并发送到无人平台。上、下楼模式在同层模式的基础上对楼梯环境下进行适配，并在局部地图中滤除了楼梯台阶作为障碍物的环境信息。在上楼模式中，首先需要对地图进行处理，利用高度差值算法过滤掉台阶信息来实现在楼梯上的规划，同时，需要增大转向动作的惩罚，避免在楼梯上进行转向操作，增大目标速度来克服爬楼梯时的坡道阻力。与上楼模式相同，首先也需要过滤掉台阶的障碍物信息，增大转向动作的惩罚，减小目标速度提高下楼梯时无人平台姿态的稳定性。

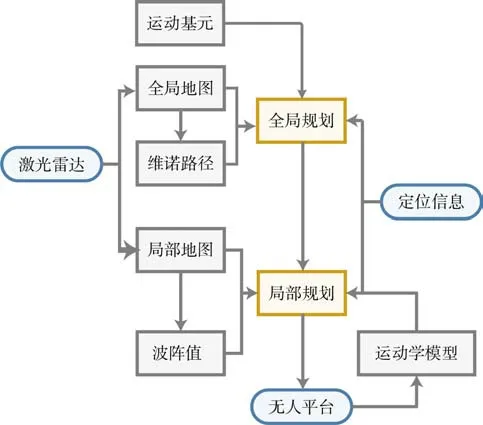
图2 同楼层运动规划框架示意图Fig. 2 Schematic diagram of motion planning framework

对于多层建筑物内环境信息，本文采用基于分层的地图表示方法，将问题进行降解求解。分层地图将多层建筑物室内环境信息表示为多个2.5D 地图和关键点，其中，2.5D 地图是基于高度差信息建立的建筑物单层的栅格地图，保存了楼层序号、单层内的可通行区域和障碍物信息；关键点是保存在相应地图下的全局坐标，为楼梯或建筑物入口的坐标信息，代表着各个地图之间的拓扑关系。关键点又分为两种，一种是记录进入当前层的入口信息，记作In，n为楼层数；另一种是出口信息，记作On。

图3 展示了一个3 层建筑物环境地图的表示方法的例子，图中左侧展示的是一个3 层建筑物的3D 结构示意图，利用分层表示方法可以表示为图中右侧的形式。其中，Map1、Map2 和Map3 分别表示建筑物1 层、2 层和3 层环境对应的栅格地图，绿色点表示进入该层的关键点，红色点表示离开该层的关键点。因此，利用栅格地图和关键点信息就可以表示出一个多层建筑物内的环境信息，为跨楼层的无人平台运动规划提供基础。

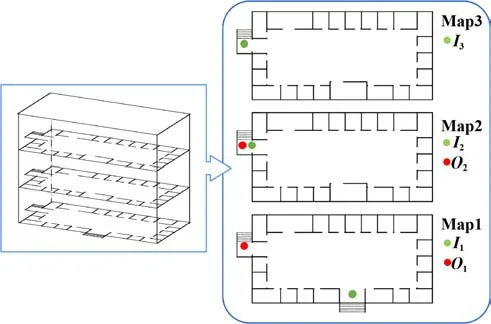
图3 多层建筑物环境地图示意图Fig. 3 Schematic diagram of the multi-storey building hierarchical map

2 基于维诺路径和运动基元的全局规划 算法

本节主要讨论用于多层建筑物中的全局规划算法。考虑到多层建筑物环境具有空间狭小的特点，本文基于A*算法，考虑无人平台运动学约束，并引入维诺路径作为参考项，实现了在多层建筑物环境中规划出平滑、无碰撞和运动学可行的全局 路径。

2.1 维诺路径

传统A*算法[12-14]在搜索路径时，只考虑路径的长度代价值，本文利用维诺图中的维诺路径来为A*算法提供新的代价项，从而规划出远离障碍物的全局路径，为平台提供更安全的全局引导。

维诺图[15-16]是由一组连接两邻近障碍物直线的垂直平分线组成的连续多边形，这些多边形的边界称做维诺路径。典型室内环境栅格地图如图4(a)所示，其对应的维诺图如图4(b)所示，黑色线段即为维诺路径。

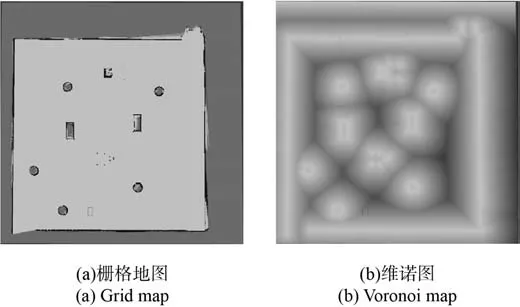
图4 室内环境栅格地图及其维诺图Fig. 4 Grid map of an indoor environment and its Voronoi map

传统A*算法利用节点的代价值来进行搜索，总代价值F(k)可以表示为

式中：G(k)为从起点到节点k的路径代价值；H(k)为节点k到目标点的启发值，用来估计当前节点到目标点的距离，为两者之间的欧氏距离；Sk-1,k为节点k-1 与节点k之间的路程。

根据维诺路径的特点，假设A*算法中一待扩展节点p(k)以及维诺路径V(x，y)，则其维诺路径代价项可以表示为

式中：vnearest为维诺路径上距离p(k)最近的点。因此，搜索过程中总的代价值可以表示为

式中：α和β为路程代价与维诺路径代价项权重 系数。

2.2 运动基元

由于A*算法得到的路径是没有考虑到无人平台运动学约束的，不利于对路径进行跟踪，本文引入运动基元来求解运动学可行的全局路径。

运动基元是路径规划问题中基本运动单元的简称。常用的基元是固定无人平台纵向速度，给定角速度预测无人平台在有限时间内行驶过的轨迹，通常给定不同的角速度生成多条轨迹。

根据传统的基元设计思路，只通过增加运动基元数量来减少非直接可达区域的范围，如图5 所示，由于没有充分利用履带式平台零半径转向的特点，导致规划出的路径更加复杂，同时也极大地增加了计算量。

图5 传统运动基元方案示意图Fig. 5 Schematic diagram of traditional motion primitives

本文将无人平台前向运动基元简化为7 个，如图6 中彩色轨迹，并提出零半径转向基元的概念，如图中箭头，通过零半径转向基元与普通前向基元的组合可以实现更加灵活的全局路径搜索。

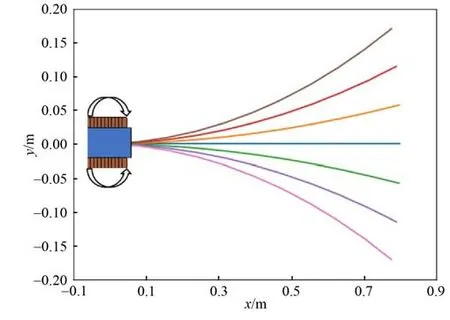
图6 零半径运动基元方案示意图Fig. 6 Schematic diagram of zero-radius motion primitives

全局路径搜索如算法1 所示。算法输入为起始点、目标点和栅格地图。首先，算法初始化两个集合，分别用来存放待扩展和已扩展节点。在每次扩展节点过程中，开集合中代价值最小的节点会被移入闭集合，而该节点的子节点会被添加到开集合当中，如此迭代，直到扩展到目标节点，返回由节点构成的全局路径。

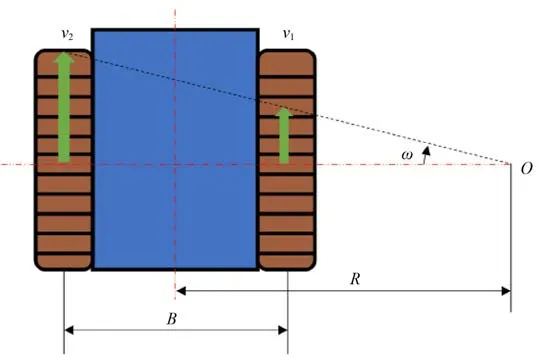
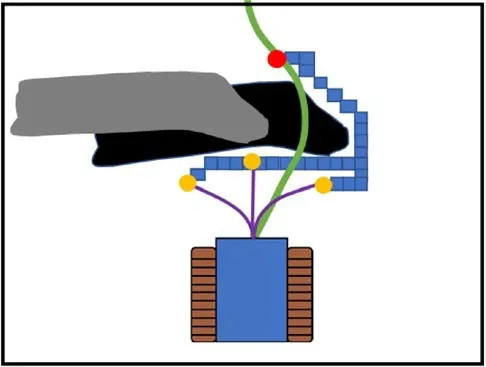
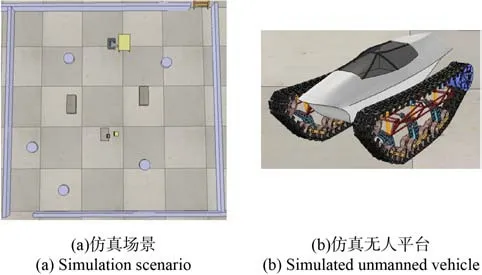
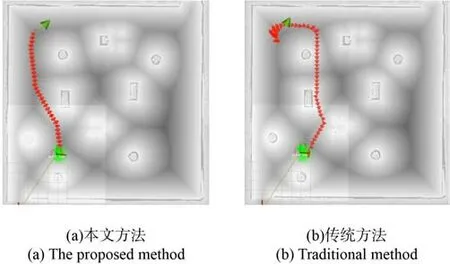
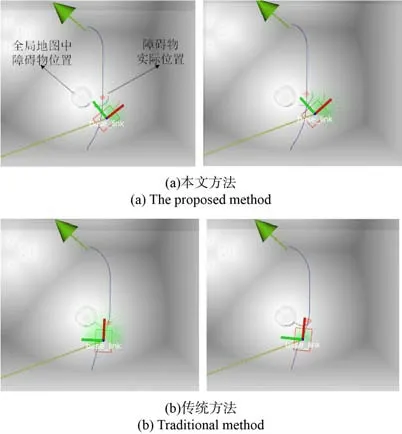
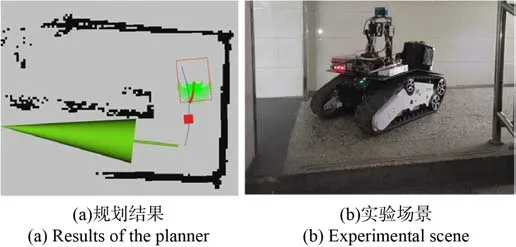
算法1：全局路径搜索 输入：目标点坐标ngoal，起始点坐标nstart，全局栅格地图Map 输出：由节点构成的全局路径 1.Sopen←nstart2.Sclosed←Ф3. WhileSopen≠Ф4. Sort(Sopen) 5. ni←Sopen.PopTop() 6. if IsObstacles(ni,Map) 7. continue 8. else if Overlap(ni,ngoal) 9. return { nstart,…,ngoal} 10. else 11. Schildren←ExpandNode(ni，primitives) 12. for child inSchildren13. F(child)←H(each)+G(ni)+αD(child)+βS(ni，child) 14. if child ∉Sopen15. Sopen←Sopen∪ {child } 16. else F(child)

2.3 路径平滑

通过改进基元A*算法直接得到的路径仍然存在两个问题，如图7 所示，一方面是路径上的路点为稀疏状态，如红色圆点所示；另一方面是由于零半径基元的存在，路径存在不光滑区段，如图中间的路点处发生了零半径转向，不利于无人平台实现平顺的路径跟踪。

图7 路径平滑示意图Fig. 7 Schematic diagram of path smoothing

基于以上两点，本文首先过滤掉零半径转向后的位姿，再利用路径平滑算法从稀疏路点来得到平滑路径，如图7 中绿色曲线所示，在平滑路径的基础上进行插值，得到稠密路点，如黄色点所示。

考虑到全局路径的导数与曲率连续，同时避免龙格现象，本文采用分段三次Hermite 插值[17-18]来对稀疏路点进行处理。

给定稀疏路点集合P(x，y，θ)，x和y为位置坐标，θ为航向角，把节点两两分段，在每一个小段上作三次Hermite 插值，就可以得到一个分段三次Hermite 插值函数H(x)。

首先，构造两组基函数hi(x)，Hi(x) (i=0, 1, …,n)：

式中：li(x)为拉格朗日插值基函数，

因此，结合式(5)、式(6)和式(7)，可以得到分段三次Hermite 插值函数为

3 基于模型预测与波阵值的局部规划算法

在全局路径的基础上，本文利用履带式无人平台运动学模型在动力学窗口内对其轨迹进行预测与评估，并引入波阵值优化距离评估方法，避免陷入局部最小。

3.1 运动学模型与轨迹预测

履带式无人平台两侧的独立驱动的履带以不同速度进行运转，由于两侧履带的速率不同，此时在履带平台右侧会形成一个转动中心，平台模型会以图8 所示的转向半径R，绕着转动中心O以ω的角速度进行转向。图8 中，v1、v2为左侧和右侧履带速度，B为履带中心距。

图8 履带式无人平台运动几何关系示意图Fig. 8 Schematic diagram of the kinematic geometric relationship of the tracked unmanned platform

根据几何关系，可以计算出转向半径R：

同时，低速状态下忽略滑转与滑移，履带式无人平台运动学模型为

式中：vx和vy为平台在x轴和y轴方向的速度；θ为平台航向角。

由刚体运动学可以得知轨迹传播方程：

式中：xt、yt、θt为t时刻平台位姿；ωt为t时刻角速度。

基于运动学模型，结合式(9)、式(10)和 式(11)，可以得到轨迹预测方程：

在轨迹预测方程的基础上，本文引用模型预测控制[19]的思想，如图9 所示，根据当前时刻t0无人平台的运动状态，在控制空间内采样得到一组控制量，以dt时间为步长，来预测未来一段时间内无人平台的状态，然后执行最优路径对应的控制量来驱动无人平台运动dt的时间长度，来到t1时刻的状态。以此类推，不断进行预测与执行控制量，直到到达目标点。

图9 轨迹预测示意图Fig. 9 Schematic diagram of trajectory prediction

3.2 基于动力学窗口的控制空间采样

在无人平台运动学的基础上进行轨迹预测之前，需要对无人平台的控制空间进行采样，由于无人平台动力学的约束，其采样区间也被限制在动力学窗口[20]之内。

1)最大加速度与最大减速度约束

在无人平台实际运动过程中，由于驱动电机转矩等的限制，其具有最大的加速度和减速度。假设最大加速度和减速度为aa和ad，最大角加速度和角减速度为αa和αd。

式中：vt为t时刻的平台速度。

2)最大与最小速度约束

式中：vmin和vmax分别为平台最小速度与最大速度；ωmin与ωmax分别为平台最小角速度与最大角速度。

3)安全距离约束

在无人平台当前位置处，为避免与障碍物发生碰撞，无人平台当前速度对应的刹车距离应该小于距离最近障碍物的距离。因此可以得到

式中：dist为t时刻最近障碍物的距离。

3.3 基于波阵值的轨迹评估

履带无人平台在进行轨迹预测之后，如图10中紫色轨迹，可以得到轨迹的终点，如黄色圆点。由于定位误差以及环境噪声等的干扰，全局地图中障碍物(灰色)会与实际障碍物(黑色)位置存在偏差。如果根据传统轨迹评估的原则，中间轨迹距离局部目标点(红色圆点)最近，会成为最优路径。然而，中间路径会导致无人平台陷入局部最小。

图10 波阵值避免局部最小示意图Fig. 10 Schematic diagram of Wavefront Value avoiding local minimum

本文引入混合A*算法[21]中的波阵值(Wavefront Value)来提高算法应对障碍物信息偏差时的鲁棒性。波阵值是一种考虑到障碍物信息后地图上一点到目标点的距离度量，可以利用算法2 计算得到。算法2 的输入为局部目标点和预测轨迹的端点集合，然后从目标点出发，向邻近的8 个栅格方向进行反向搜索，若为障碍物则跳过，则直到搜索到所有预测轨迹端点时，过程中搜索路程长度即为波阵值最为算法的输出。

当利用波阵值对轨迹进行评估时，由于其具有考虑到环境中障碍物的特性，右侧轨迹终点到达局部目标点的波阵值最小，即蓝色方块的数量最小，为最优轨迹，因此可以绕过障碍物，避免局部最小。

算法2：计算波阵值 输入：局部目标点坐标g[x,y]，预测轨迹终点集合T[traj1，traj2, … , trajn]，局部栅格地图Map 输出：预测轨迹对应波阵值集合W1.Goal←[g[0], g[1],0]2.S.Push(Goal) 3.W←[Finite]4. While S ≠Ф5. Current←S.PopTop() 6. for each in ExpandTable 7. Next←Current+ each 8. Next_Position←[Next[0]，Next[1]]9. Next_Wave←Next[2]10. If IsObstacles(Map，Next_Position) | IsExpanded(Next_Position) 11. continue 12. end 13. S.Push(Next) 14. fortrajinT15. iftraj= Next_Position16. W[GetIndex(traj)]←Next_Wave17. end 18. end 19. if IsAllFinite(W) 20. break 21. end 22. end 23. end 24. returnW

4 实验与结果分析

为评价本文提出的多层建筑物内运动规划框架的性能，针对全局与局部规划模块，在仿真环境中，采用本文方案和传统运动规划方法进行对比实验，进而通过实车实验来证明本文方案的可行性。

4.1 仿真实验

为测试全局和局部规划算法的性能，本文在Vrep 中搭建图11(a)所示虚拟环境作为算法的输入，搭建图11(b)所示无人履带平台模型作为算法的被控对象，配备有激光雷达和定位模块。算法在Linux 环境和ROS 平台下运行，对虚拟环境的输入信息进行处理后，将得到的路径下发给无人平台模型，最后对结果进行统计分析，实现对算法的仿真测试。

图11 仿真环境示意图Fig. 11 Schematic diagram of the simulation environment

全局规划仿真结果如图12 所示，绿色箭头为目标点，红色扇形为算法扩展结点集合。如表1 所示，从中可以看到，在扩展节点数量增加3%、平均耗时增加6%的条件下，全局路径长度减少了31%，且距离障碍物更远、路径更加安全。

表1 全局规划仿真结果Table 1 Simulation results of the global planner

图12 全局规划仿真结果对比图Fig. 12 Comparison of the global planner’s simulation results

局部规划仿真实验通过偏移障碍物的位置来模拟障碍物位置偏差的情形。圆形障碍物在全局地图中位置如图13所示，由于定位和建图误差，实际障碍物在圆形障碍物右侧，激光雷达扫描到其前部，在地图中为半圆形。图13中，蓝色曲线为全局路径，红色矩形为无人平台地面投影，绿色曲线为局部规划的待选轨迹，红色曲线为最优轨迹。图13(a)展示的是本文的局部规划算法筛选出最优轨迹并成功绕过了障碍物，图13(b)中的传统局部规划算法在障碍物面前陷入局部最小。

图13 局部规划仿真对比图(左为遇到障碍物，右为绕过障碍物)Fig. 13 Comparison of the local planner’s simulation results (left picture shows encountering obstacles, right picture shows bypassing obstacles)

4.2 实车实验

本文真实场景实验所使用的是履带式无人平台，如图14 所示。本文依赖的传感器有安装于无人平台顶部的16 线激光雷达和前部的32 线补盲雷达，承担着感知与定位的任务。除传感器外，无人平台还配备有一台主频为3.6 Hz 的工控机，感知、定位与规划程序都在该计算平台上运行。本文实验中感知模块使用的是基于激光雷达的概率栅格地图程序，定位模块使用的是激光SLAM 程序，规划模块使用的是本文提出的多层建筑物运动规划框架。

图14 实验无人平台外观Fig. 14 Appearance of the unmanned platform in the experiment

首先，通过遥控无人平台在多层建筑物内进行建图，获取建筑物的三维点云信息并以分层地图的方式存储下来。在此基础上设置建筑物一层大厅内一点为起点，3 层长走廊内一点为终点，如图15所示，开始自主导航任务。

图15 实验起始点与目标点Fig. 15 Starting point and target point in the experiment

在1层环境中规划结果如图16所示，其中蓝色曲线为全局路径，绿色曲线为局部路径，绿色箭头为目标点，可以看出，规划出的全局路径平滑连接到目标点，且远离障碍物，无人平台顺利进入狭长走廊，如图16(a)所示。由于室内狭长走廊的对称性以及墙壁瓷砖反射效应的影响，激光SLAM定位在此区域误差增大，如图16(b)红色圆圈部分，这段直角转弯区域墙壁发生了弯曲且长度缩短，导致地图中转弯入口处相比实际的1.0 m宽度变大。在这种狭窄区域障碍物位置出现较大偏差的情形下，无人平台避免了陷入局部最小值，成功通过该区域如图16(b)所示。

图16 1 层楼内实验结果(左为规划路径，右为实景)Fig. 16 Experimental results of the first floor (the left is the planned path, and the right is the real scene)

在此基础上，无人平台开始在楼梯上进行自主导航任务。图17 和图18 所示为无人平台在楼梯和转台上规划出的路径与实验场景，从中可以看出通过高度差将楼梯信息过滤后，无人平台在楼梯模式中可以规划出更加平直的路径。

图17 楼梯区域实验结果Fig. 17 Experimental results of the stair area

图18 转台区域实验结果Fig. 18 Experimental results of the platform area

图19为在3层时的实验结果。图19(a)中无人平台跟踪全局路径成功通过1 m宽的直角转弯，进入狭长走廊。在走廊中有一扇打开的门，可通行空间宽度为0.90 m，而平台宽度为0.80 m，剩余空间狭窄。如图19(b)所示，无人平台成功穿越狭窄区域。最后，如图19(c)所示，无人平台到达目 标点。

图19 第3 层楼实验结果(左为规划路径，右为实景)Fig.19 Experimental results on the third floor (the left is the planned path, right is the real scene)

实车实验结果见表2，无人平台经过第1 层区域、楼梯区域和第3 层区域3 个阶段，其中第1 层起始区域空间相对宽阔，平均速度也最高；楼梯区域由两层共6 段楼梯组成，路径长度最长，同时为保证楼梯上平台运行的安全，最大速度也最小，导致花费时间最长；第3 层区域空间狭窄，平台处于低速状态更多，因此平均速度下降。在实验过程中，算法的频率能够稳定在10 Hz，并完成多层建筑物内的自主导航任务。

表2 实车实验结果Table 2 Results of the experiment

应用本文运动规划框架的北理精灵队在跨越险阻2021 地面无人系统挑战赛中取得了第4 名的 成绩。

5 结论

本文针对多层建筑物内无人平台的自主导航问题，提出了一个针对于多层建筑环境优化的运动规划框架。通过仿真与实车实验验证，得到以下主要结论：

1)在全局规划层面，提出零半径转向基元并引入维诺路径，全局规划算法在扩展节点数量增加3%、平均耗时增加6%的条件下，全局路径长度减少了31%，且距离障碍物更远，路径更加安全，提高了在狭窄区域规划路径的灵活性。

2)在局部规划层面，引入波阵值作为评估项，局部规划算法相比于传统算法避免了陷入局部最小值，提高了算法的鲁棒性。

3)经过实车实验，基于本文运动规划框架的无人平台在多层建筑物内完成了自主导航任务，证明了方案的可行性。